GARCH模型与协整模型在跨商品套利中的比较研究——以铁矿石和螺纹钢期货为例

周 亮

(湖南财政经济学院学报编辑部，湖南长沙 410205)

GARCH模型与协整模型在跨商品套利中的比较研究
——以铁矿石和螺纹钢期货为例

周 亮

(湖南财政经济学院学报编辑部，湖南长沙 410205)

选取2016年10月10日至2017年2月28日的铁矿石I1705、螺纹钢RB1705合约的所有60分钟价格数据，分别建立协整模型和GARCH模型以确定两者价差的关系并进行套利，结果发现:协整模型样本内获得了72%的胜率和71.97%的收益率，样本外获得了60%的胜率和23.57%的收益率；GARCH模型样本内获得了80%的胜率和98.77%的收益率，样本外获得了67%的胜率和34.97%的收益率。GARCH模型无论是胜率还是收益率方面，都要优于普通的协整模型。

协整；GARCH模型；套利；期货

0 引 言

跨品种套利主要是指在买入或卖出某种商品(合约)的同时，卖出或买入相关的另一种商品(合约)，当两者价差收缩或扩大至一定程度时平仓了结，以获得一定利润的交易方式。虽然此方法具有一定可行性，但是跨品种套利作为外联套利，其价差或比值通常是沿着趋势变化的，一旦出现历史比值的高点(或价差)为今年比值的低点时，就会造成套利的巨大损失。但总体来说，套利的风险比起单边投机而言要小很多，尤其对于有产业背景的现货商而言，对跨品种套利进行深入研究，亦是规避原材料及成品价格波动的重要手段。因此无论是学术界还是产业界，越来越多的人将目光集中在跨品种套利以及套期保值上面。

目前国内外学者对期货跨品种套利的研究大多集中在贵金属、原油、农产品及股指期货上，对于黑色产业链的研究相对来说较少。随着2016年中央“去产能”政策的加码，铁矿石和螺纹钢的价格快速走高，而到了2017年政策边际效应降低又导致两者的价格大幅回落。价格的大幅波动极大地增加了贸易商和期货交易员的风险性。基于此，笔者对铁矿石和螺纹钢期货进行了相关研究，从现实应用角度看，现货贸易商可以通过协整模型及GARCH模型进行套期保值，从而规避价格波动的风险；从理论价值角度看，通过详细比较普通的协整模型与GARCH模型所带来的收益和风险，可以清晰地观察到两个模型在套利应用过程中的优劣。

1 文献综述

国内外学者对跨品种套利进行了大量研究。从研究对象来看，主要集中在农产品期货、原油期货、金属期货及股指期货等的套利研究。Tzang和Leuthold[1]对大豆、豆粕和豆油之间的长期关系进行了研究，建立了三者之间的最优套保比例，开启了对大豆压榨套利的研究。Rechner和Poitras[2]模拟大豆压榨过程，认为套利交易收益应忽略压榨成本，改用以压榨利润总值为标准来进行套利，并通过实证模型发现可以取得不错的收益。Liu[3]检验了生猪与玉米、豆粕价格之间的协整关系，发现存在获利的可能性，可以运用套利交易管理敞口风险、减少利润波动、增加盈利性。Girma和Paulson[4]则对原油、汽油和取暖油期货进行套利研究，认为三者之间不合理的价格关系给期货套利交易提供了可能性，并且运用移动平均法模拟交易统计获利效果显著。Haigh和Holt[5]认为进行原油期货裂解套利应当考虑现货市场价格因素，因此建立了一个涵盖期货价格、现货价格和交易成本的模型，用不同方法对原油及其衍生品期货进行套利研究，结果发现，尽管要进行频繁的期货头寸比例调整，但是扣除交易成本因素，GARCH－M在交易获利和管理风险中仍为最优。国内学者如刘建和等[6]运用协整检验、误差修正模型研究了大豆、豆粕和豆油三者期货价格之间长期存在的协整关系，发现我国大豆期货及豆粕和豆油期货三者进行跨商品套利可行，能够获得正向的套利收益率，在不同的开平仓阀值下，Elman神经网络模型较均值回归模型能够得到更好的套利结果。陈思竹[7]发现虽然不同时间的棉花期货合约间存在长期稳定关系，但在短期内这种长期稳定关系会发生偏离，两个合约间的价格差会出现异常波动，通过运用协整模型证明在我国棉花期货市场中存在跨期套利机会。杨刘名等[8]以上海期货交易所的螺纹钢1605合约与大连期货交易所的铁矿石1605合约五分钟周期收价的高频数据为研究对象，发现两者可以构建协整套利组合，同时也需要注意市场结构的转变对组合参数进行及时调整。郑尊信和李佳[9]以上海金属网长江现货和上海期货交易所铜、铝和锌期货等价格数据为基础，实证分析了商品市场价格异常波动及期现价格联动非对称相关结构对企业套期保值决策的影响。邢亚丹等[10]基于沪深300股指期货数据采用标准差距离法构造了分钟级别高频跨期套利策略，在考虑交易成本的情况下该策略年化收益超过一倍。

在具体的套利方法上，学者们大部分采取均值回归方法，即通过协整、误差修正模型、GARCH等时序分析方法来研究商品期货之间长期存在的相互关系，从而设计相应的套利策略。Wahab等[11]运用协整、误差修正模型等方法研究了黄金和白银两者价格之间的关系，发现利用移动平均法可以较好地实现两者之间的跨品种套利。Simon[12]运用GRACH方法对大豆压榨价差进行了研究，发现存在长期均衡即短期偏差最终会回归均衡。Dunis等[13]运用非线性协整方法对WTI原油和无铅汽油之间的套利交易进行了相关研究，以公允价值的非线性协整模型作对照，分别应用多层感知网络、递归神经网络和高阶神经网络三个模型进行数据分析及交易模拟，结果表明两种期货价格之间是非线性关系，高阶神经网络模型无论是数据拟合还是交易获利都效果最好。国内学者如李世伟[14]利用沪深300股指期货的实际交易数据，借助对现有协整理论进行改进的套利方法建立模型并实施跨期套利，结果发现，改进的协整策略可以取得较好的套利效果。李宇霆[15]则通过GARCH模型研究了沪深300股指期货与上证50股指期货的跨品种套利，发现GARCH模型改变了之前研究中运用固定标准差序列的缺陷，给出了时变标准差的区间，提高了统计套利的精确性。庞贞燕和刘磊[16]采用VECM－BEKK－GARCH模型实证检验了我国农产品期货市场对现货价格波动性的影响，并构建带有虚拟变量的GARCH模型考察农产品期货合约上市对现货价格波动的影响方向和程度，发现农产品期货合约上市减小了现货市场的波动性。覃良文等[17]利用Engle－Granger检验法，检验了上海沪铜期货两个近月合约收盘价数据的长期均衡关系，并利用HP滤波法将两序列分解为长期趋势和短期波动周期性两种成分，实证结果表明，基于HP滤波的套利方法，平滑指数越小，套利利润越高，与传统未进行HP滤波的套利方法相比，套利成功率较高，风险能得到有效控制，且投资者有较高的收益。靳朝翔等[18]通过设置不同的开平仓阀值，运用BP神经网络模型和NAR动态神经网络模型在样本区间内进行套利策略对比研究，结果发现NAR动态神经网络模型的预测能力更强，其套利策略在螺纹钢、铁矿石和焦炭三者间进行跨品种套利效果更好。

综上所述，大量学者对跨商品套利进行了实证研究，主要集中在用均值回归方法对商品期货或金融期货长期均衡关系的检验及相应统计套利策略的设计上。研究农产品、原油及股指期货的较多，对黑色产业链进行研究的相对较少；采用特定模型进行关系检验及套利设计的较多，但是对不同模型进行详细比较的较少。因此，笔者拟分别采用协整模型和GARCH模型对铁矿石和螺纹钢期货合约的价差序列进行统计检验，并通过一定交易规则的设置实行套利，并最终通过实证结果比较两种模型在跨商品套利过程中的优劣。

2 模型建立

2.1 数据选取及来源

铁矿石与螺纹钢处于产业链的上下游关系，两者的价格波动相关性很强，因此选择大商所的铁矿石期货和上期所的螺纹钢期货，研究两者间价格的相互影响关系。每年1月、5月及10月合约持仓量和成交量较大，因此选择最近的1705合约作为研究对象。日线及更高级别的数据相对来说数量较小，而分钟级别的数据波动过于频繁，因此选择小时级别的数据进行研究。最终选定铁矿石I1705和螺纹钢RB1705合约2016年10月10日至2017年2月28日的所有60分钟K线数据，共763个数据进行研究。其中选择前500个数据(2016年10月10日至2017年1月5日)为样本内数据以进行协整关系确定，后263个数据(2017年1月6日至2017年2月28日)为样本外数据以验证统计套利效果。

所有数据均来自东方财富金融数据库，数据处理均使用EXCEL以及EVIEWS6.0软件。

2.2 描述性统计及平稳性分析

I1705和RB1705两组数据的描述性统计如表1所示。由表1可以看出，两个品种的价格均波动剧烈。对两者进行相关性检验，发现相关系数达到0.98，相关性非常高，适合进行统计套利。

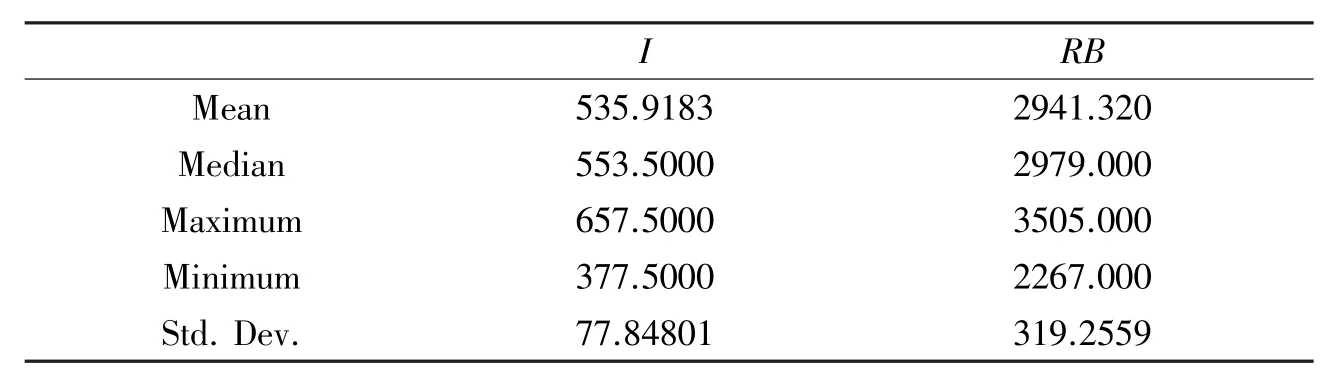
表1 描述性统计

在对数据进行协整分析前，需要先对数据的平稳性进行检验。表2报告了I1705和RB1705两组数据的原序列及一阶差分序列的单位根检验结果，可以看出，两个序列均为一阶单整序列，适合进行协整关系检验。

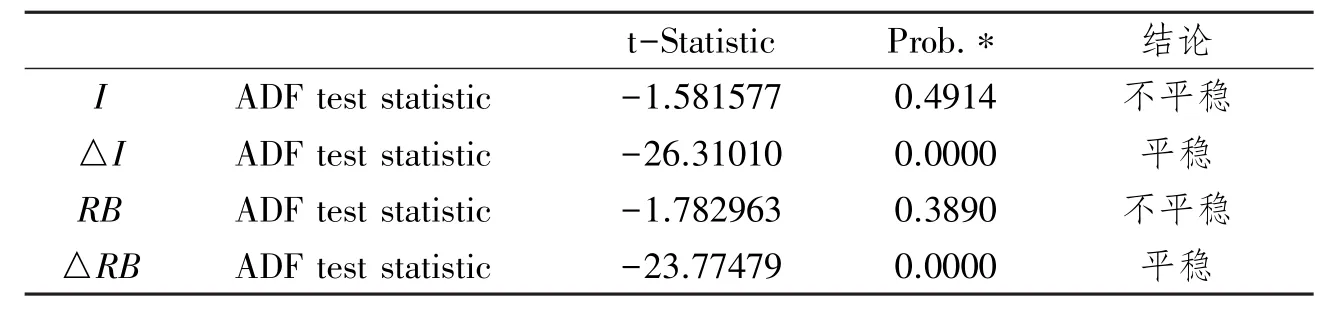
表2 平稳性检验

2.3 协整模型建立

2.3.1 EG两步法协整模型

采用EG两步法检验I1705和RB1705两者间的协整关系。第一步，对两序列进行OLS回归分析，结果如表3所示，模型调整R2达到0.95，拟合效果较好。第二步，对回归残差进行单位根检验，结果如表4所示，残差为平稳序列。因此两序列存在协整关系，协整方程为:I＝－164.9089＋0.23827RB。

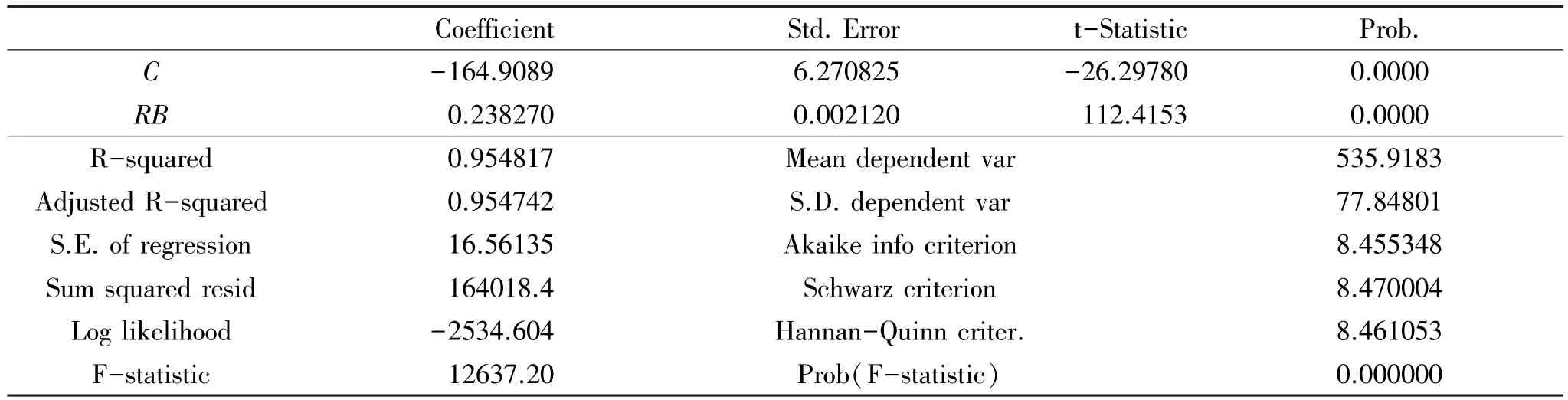
表3 OLS回归结果

表4 回归残差检验

要进行套利，则应在买入(卖出)1单位I1705的同时，卖出(买入)0.23827单位RB1705。考虑到两者量纲的区别(1手铁矿石为100吨，1手螺纹钢为10吨)，因此两者真实交易的比例应为1:2.3827。

2.3.2 误差修正模型

协整模型考察两时间序列之间的长期关系，而误差修正模型则解释了两序列之间的短期影响，可以建立误差修正模型研究一次完整的套利所需的大概时间。建立误差修正模型:ΔI＝c＋αΔRB＋βECM＋ε，ΔI为I1705序列的差分项，ΔRB为RB1705序列的差分项，ECM为误差修正项，α、β为系数，c为常数项，ε为残差。

表5报告了误差修正模型的检验结果，ECM项前的系数为－0.050 7，显著小于0，表示价差存在均值回归的特征，前一次的非长期均值偏差会以5.07%的比例进行反向修正。根据Madhavan和Smidt[19]提出的半周期公式，该误差修正模型显示短期偏差回复至长期均值的半周期大概需要13个小时，回复速度较快。考虑到合约的存续时间远大于回复周期，因此执行统计套利比较合适。

表5 ECM模型检验结果

2.4 GARCH模型建立

2.4.1 ARCH效应检验

许多时间序列存在着在某一段时间范围内波动剧烈、下一段时间价格波动相对较小的现象，这意味着时间序列大多存在着异方差的特征，即当下时刻的价格条件方差受上一期方差值影响。标准化的GARCH(1，1)模型可以表示为:。其中，xt为外生变量，ut为残差，为方差。GARCH模型中的方差方程表示本期方差是以前期信息为基础的一期向前预测方差，从而实现对条件方差的测度，从而能够更好地拟合金融时间序列的波动集聚现象。

图1 回归残差图

图1报告了OLS模型的回归残差，可以看出存在较为明显的异方差特征，因此适合建立GARCH模型。在进行GARCH检验前，首先需对残差序列进行ARCH－M检验，以验证异方差的存在性。表6报告了ARCH检验结果，P值为0，拒绝了原序列不存在ARCH的假设。因此适合对原序列建立GARCH模型。

表6 ARCH检验

2.4.2 GARCH模型结果

建立GARCH(1，1)模型来刻画非均衡误差序列的条件异方差性，如表7所示，模型系数非常显著，模型调整R2达到0.95，拟合效果较好。建立的均值和方差方程分别为:

同样，从回归方程可以看出，要进行套利，两者真实交易的比例应为1:2.52549。

表7 GARCH模型

3 套利方案设计及检验

3.1 套利方案设计

协整模型和GARCH模型均显示铁矿石和螺纹钢存在着长期的协整关系，适合进行套利。为了更好地实现套利效果，借鉴Wahab等[11]移动平均的思想，笔者不简单采用固定值作为价差的中值，而用60期的价差移动平均值作为回归的中轨；同时对于协整模型，不采用方差的均值作为套利阈值的标准，而选用60期的平均波动率为套利阈值的标准。由图2可以看出，GARCH模型的方差明显具有集聚现象，而简单移动平均求得的方差则相对来说更为平缓。

图2 两个模型的方差序列

3.2 交易保证金及手续费

交易所对螺纹钢、铁矿石的最低保证金要求均为8%，但是实际券商要求的保证金均为12%，笔者采用券商要求的保证金比例来进行测算。假设交易所订单可以拆分，则完成一次套利，按协整模型最低保证金要求为157元；按GARCH模型，最低保证金要求为163元。

券商普遍对螺纹钢、铁矿石收取手续费的标准单边分别为成交金额的3.6%%、5%%，假设订单可以拆分，则按协整模型计算进行一次完整的套利操作预计需要手续费1.15元，按GARCH模型预计需要手续费1.19元。

3.3 套利交易结果

根据以上交易原则，分别在样本内和样本外进行检测，所得结果如表8所示。从回撤角度看，最大的是GARCH样本内，达到19.4；最小的是GARCH样本外，只有9。因此，整体来看，无论从胜率还是收益率上看，GARCH模型均要优于协整模型。

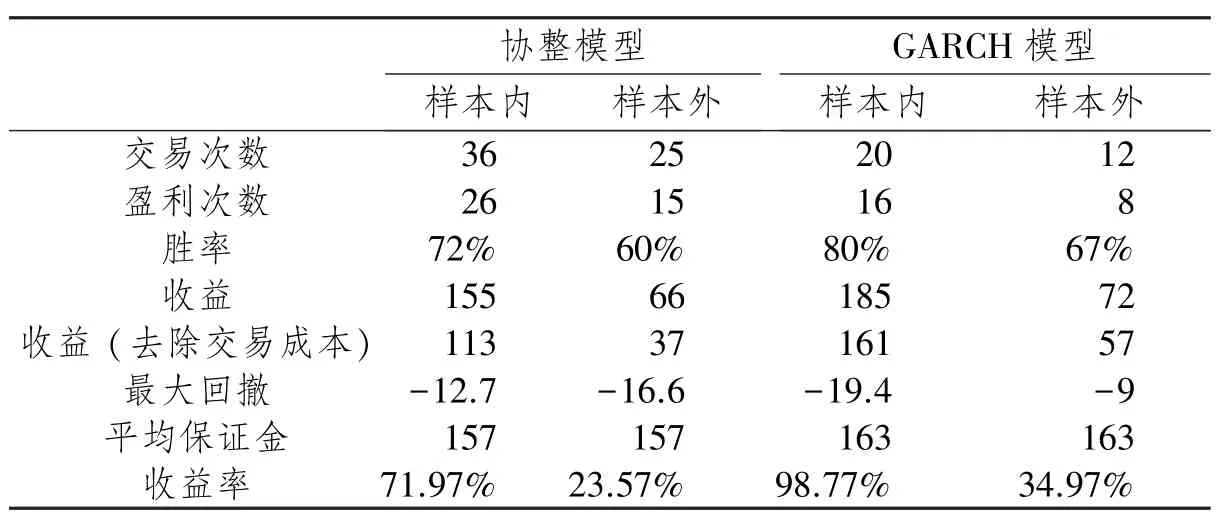
表8 套利交易结果

4 结论与对策建议

4.1 结论

笔者选取2016年10月10日－2017年2月28日的铁矿石I1705、螺纹钢RB1705合约的所有60分钟价格数据，分别通过协整模型和GARCH模型确定两者之间的相互影响关系。采用60周期价差均值为基准点，设定开仓阈值为1.5、平仓阈值为0.05、止损阈值为2，协整模型采用60周期平均波动率，GARCH模型采用方差方程所算出的方差序列，实行统计套利。套利结果显示:协整模型样本内获得了72%的胜率和71.97%的收益率，样本外获得了60%的胜率和23.57%的收益率；GARCH模型样本内获得了80%的胜率和98.77%的收益率，样本外获得了67%的胜率和34.97%的收益率。总体而言，GARCH模型无论是胜率还是收益率方面，都要优于普通的协整模型。

由实证结果可以看出，套利交易实现了较好的收益。但是在研究方法上还有很大拓展空间:首先，笔者采用的协整方法属于均值回归策略，但是已有大量文献采用神经网络对价差进行预测，从而实现套利；其次，笔者采用的数据为60分钟数据，虽已极大地保证了样本的充足率，但是相对更加高频的数据来说，无疑丢失了更多信息以及可套利交易的样本；最后，笔者只是将样本简单分为样本内和样本外，但是期货品种之间的协整关系并不是简单固定的，因此在采用更大样本数据的前提下，可以对协整模型进行滚动求解，这样品种之间的比率关系可以采用更近的数据，从而使得套利交易更加有效。

4.2 对策建议

第一，现货贸易商可以通过协整模型及GARCH模型进行套期保值，从而规避价格波动的风险。期货市场的风险主要来源于其较高的杠杆，而主要的价值功能则在于给现货贸易商提供套期保值的品种。经济形势的波动导致大宗商品价格的持续波动，大赚大亏的情形在贸易商中并不少见，因此现货贸易商应积极利用期货市场的套期保值功能实现对原材料和产成品价格的锁定，从而最大限度地降低价格波动导致的经营风险。

第二，期货市场的投资者可以改变以往单边投资的模式，通过跨品种套利有效降低投资风险。对于很多参与到期货市场的投资者而言，高杠杆带来了一夜暴富的机遇，但也带来了血本无归的可能性。有经验的投资者可以多采用跨品种套利的方式，来有效降低投资风险。虽然相对于单边投机，套利降低了收益率，但也极大地增加了参与者的存活率。如果能将套利模式做好，再加上期货市场的高杠杆和高频率，完全可能获得较高的收益率。

第三，交易所应推广套利思路和开放更多的套利品种。适当的套利可以提高品种的流动性，也能够更好地实现期货市场的价格发现功能。目前大连商品交易所已经提供了许多商品供投资者做套利交易，这样可以有效降低投资者的交易成本和保证金需求，从而扩大套利的交易量。随着投资者套利需求的扩大，交易所应提供更多的交易品种，同时加强对套利思想的宣传，号召更多的投资者改变以往高风险的单边投机行为，这样也可以更好地发挥期货市场的价格发现功能。

[1]TZANG D N，LEUTHOLD R M.Hedge Ratios Under Inherent Risk Reduction in a Commodity Complex[J].Journal of Futures Markets，1990，10(5):497－504.

[2]RECHNER D，POITRAS G.Putting on the Crush:Day Trading the Soybean Complex Spread[J].The Journal of Futures Markets，1993(1):61－75.

[3]LIU Q.Price Relations among Hog，Corn，and Soybean Meal Futures[J].Journal of Futures Markets，2005，25(5):491－514.

[4]GIRMA P B，PAULSON A S.Seasonality in Petroleum Futures Spreads[J].The Journal of Futures Markets，1998，18(5):581－598.

[5]HAIGH M S，Holt M T.Crack Spread Hedging:Accounting for Timevarying Volatility Spillovers in the Energy Futures Markets[J].Journal of Applied Econometrics，2002，17(3):269－289.

[6]刘建和，梁仁方，王玉斌，等.大豆期货合约均值回归套利策略和Elman神经网络套利策略对比研究[J].湖南财政经济学院学报，2016(3):13－20.

[7]陈思竹.我国棉花期货市场跨期套利研究[J].时代金融，2016(8):206－208.

[8]杨刘名，于晓宝，李嘉琪.基于高频数据的铁矿石和螺纹钢的协整套利研究[J].金融经济，2016(16):99－101.

[9]郑尊信，李佳.商品期现价格联动与局部套期保值决策——基于上海期货市场的实证研究[J].广东金融学院学报，2012(6):79－90.

[10]邢亚丹，劳兰珺，孙谦.跨期套利收益与风险来源探究——基于沪深300股指期货高频跨期套利策略[J].投资研究，2015(10):98－109.

[11]WAHAB M， COHN R，LASHGARI M.The Gold－silver Spread:Integration，Cointegration，Predictability and Ex－ante Arbitrage[J].Journal of Futures Markets， 1994，14(6):709－756.

[12]SIMON D P.The Soybean Crush Spread:Empirical Evidence and Trading Strategies[J].Journal of Futures Markets，1999，19(3):271－289.

[13]DUNIS C L，LAWS J，EVANS B.Modelling and Trading the Gasoline Crack Spread:A Non－linear Story[J].Derivatives Use，Trading ＆Regulation，2006，12(1):126－145.

[14]李世伟.基于协整理论的沪深300股指期货跨期套利研究[J].中国计量学院学报，2011(2):198－202.

[15]李宇霆.基于GARCH模型的股指期货套利策略研究[N].期货日报，2016－08－15(03).

[16]庞贞燕，刘磊.期货市场能够稳定农产品价格波动吗——基于离散小波变换和模型的实证研究[J].金融研究，2013(11):126－139.

[17]覃良文，唐国强，林静.基于HP滤波和协整理论的期货套利研究[J].湖北大学学报(自然科学版)，2015(6):570－576.

[18]靳朝翔，梁仁方，刘建和.基于神经网络模型的商品期货跨品种套利策略[J].云南财经大学学报(社会科学版)，2016(4):150－160.

[19]MADHAVAN A，SMIDT S.A Bayesian Model of Intraday Specialist Pricing[J].Journal of Financial Economics，1991，30(1):99－134.

A Comparative Study of GARCH Model and Cointegration Model in Cross－commodity Arbitrage:A Case Study of Iron Ore and Rebar Futures

ZHOU Liang
(Academic Journal Editorial Department，Hunan University of Finance and Economics，Changsha410205，China)

A cointegration model and a GARCH model are established respectively to determine the relationship between the two contracts and make arbitrage by selecting all the 60－minute price data of iron ore I1705 contract and rebar RB1705 contract from October 10， 2016 to February 28， 2017.The results show that the cointegration model samples obtain a 72%winning percentage and a 71.97%yield rate with a 67%winning percentage and 34.97%yield rate outside the samples while the GARCH model samples obtain an 80%winning percentage and a 98.77%yield rate with a 67%winning percentage and a 34.97%yield rate outside the sample.the GARCH model is superior to ordinary cointegration model in terms of winning percentage and yield rate.

cointegration； GARCH model； arbitrage； futures

F832.5

A

2095－929X(2017)05－0054－07

(责任编辑高 琼)

2017－05－31

湖南财政经济学院青年教师科研基金项目(Q201408)。

周亮，男，湖南邵阳人，湖南财政经济学院学报编辑部编辑，研究方向:宏观经济、金融工程，Email:66473405＠qq.com。