改进的多目标粒子群优化算法
项铁铭 王建成
(杭州电子科技大学天线与微波技术研究所 浙江 杭州 310018)
改进的多目标粒子群优化算法
项铁铭 王建成*
(杭州电子科技大学天线与微波技术研究所 浙江 杭州 310018)
为提高解决多目标优化问题的能力,提出一种改进的多目标粒子群优化算法。该算法采用均匀随机初始化方法初始种群,采用快速支配策略选取非支配解,生成外部档案;通过比较粒子连续几代的更新情况来判断是否陷入局部最优并相应地采取不同的更新策略,同时引入变异因子对粒子进行扰动。实验结果表明,在世代距离GD(Generational Distance)和空间评价方法SP(Spacing)性能指标上,改进之后的算法与另外几种对等算法相比,具有显著的整体优势。
外部档案 均匀初始化 快速支配策略 多目标粒子群优化算法 粒子信息档案
0 引 言
与单目标问题不同,多目标之间相互关联并且相互矛盾[1-2,9-10]。解决多目标问题就是要尽可能地找到一组能最大化均衡各个目标的较好的解的集合[3-5]。目前大多数多目标粒子群优化算法只是作用在算法的局部,如侧重于非劣解的选取,或者外部档案的维护等,并没有对算法进行整体的协同改进,也不能改善算法的整体性能。而且存在着早熟收敛、陷入局部最优等问题,得到的结果集也很难令人满意。为了解决这些问题,谢承旺等[6]提出了一种多策略融合的算法来改善上述问题,左一多[7]提出了一种快速支配策略来维护外部档案,Xu等[8]融入了二分查找策略。这些改进后的算法都在某些程度上优化解决了上述提到的问题,但是对于陷入局部最优之后的操作以及多样性的维护依然存在改进的空间。本文结合文献[6-8]的优点,提出了一种改进的多目标粒子群优化算法(IMOPSO)。本文改进算法提出了一种全新的更新策略,旨在结合粒子信息档案中粒子连续几代的更新状况,采用不同的更新策略,从而对粒子的更新作出更加高效的指导和优化,提高算法解决复杂MOP问题时的整体性能。
1 改进的多目标粒子群优化算法
1.1 种群初始化策略
为了保证初始化的多样性,本文使用均匀随机初始化方法,最大程度上保证初始群体的随机性和多样性。
1.2 档案更新策略
对于超出档案的解集,如果该解集大小超出档案限定值,则根据限定值大小选取粒子保存到临时档案中用于下一次迭代的档案更新;如果解集大小不足限定值,则将该解集全部存入临时档案中,参与下一次迭代时的档案更新。这样可以更好地实现粒子的均匀分布。
1.3 粒子更新策略
与现有大部分的MOPSO更新策略不同,本文提出了一种基于粒子个体表现的更新策略,策略如下:
1) 建立额外档案用于保存粒子的每一代的位置及其适应度值信息。
2) 判断当前粒子与前两代相比两个适应度值在每一代的变化。
3) 引用扰动概率P来平衡粒子的收敛速度与勘探开采能力。
本文采用的扰动概率P更新策略如下:
(1)
其中,r为当前迭代次数,Tmax为最大迭代次数,NN为外部档案的定义规模,Nrep为当前迭代次数下外部档案中的粒子数目,gen为达到外部档案定义的规模时的迭代次数。
开始时,外部种群为空,扰动概率很高,高概率将导致高的探索能力,同时降低了粒子收敛于局部最优的可能性。随着外部种群粒子数的增加,概率开始下降,当外部种群的实际大小达到其最大规模的一半时,扰动概率接近为0,使得粒子群有足够的时间根据自身的知识和社会行为发现新的区域,更好地探索新的区域,再之后扰动概率又开始上升。当外部种群被充满之后,扰动概率随着迭代次数的增加逐渐降低,使粒子向真实地Pareto前端靠拢。
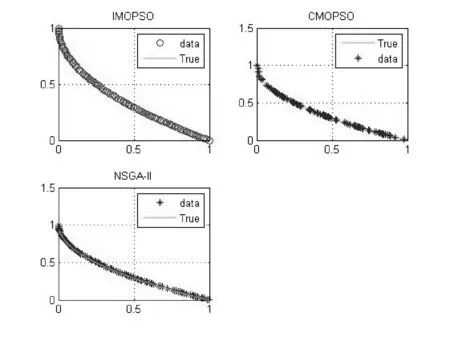
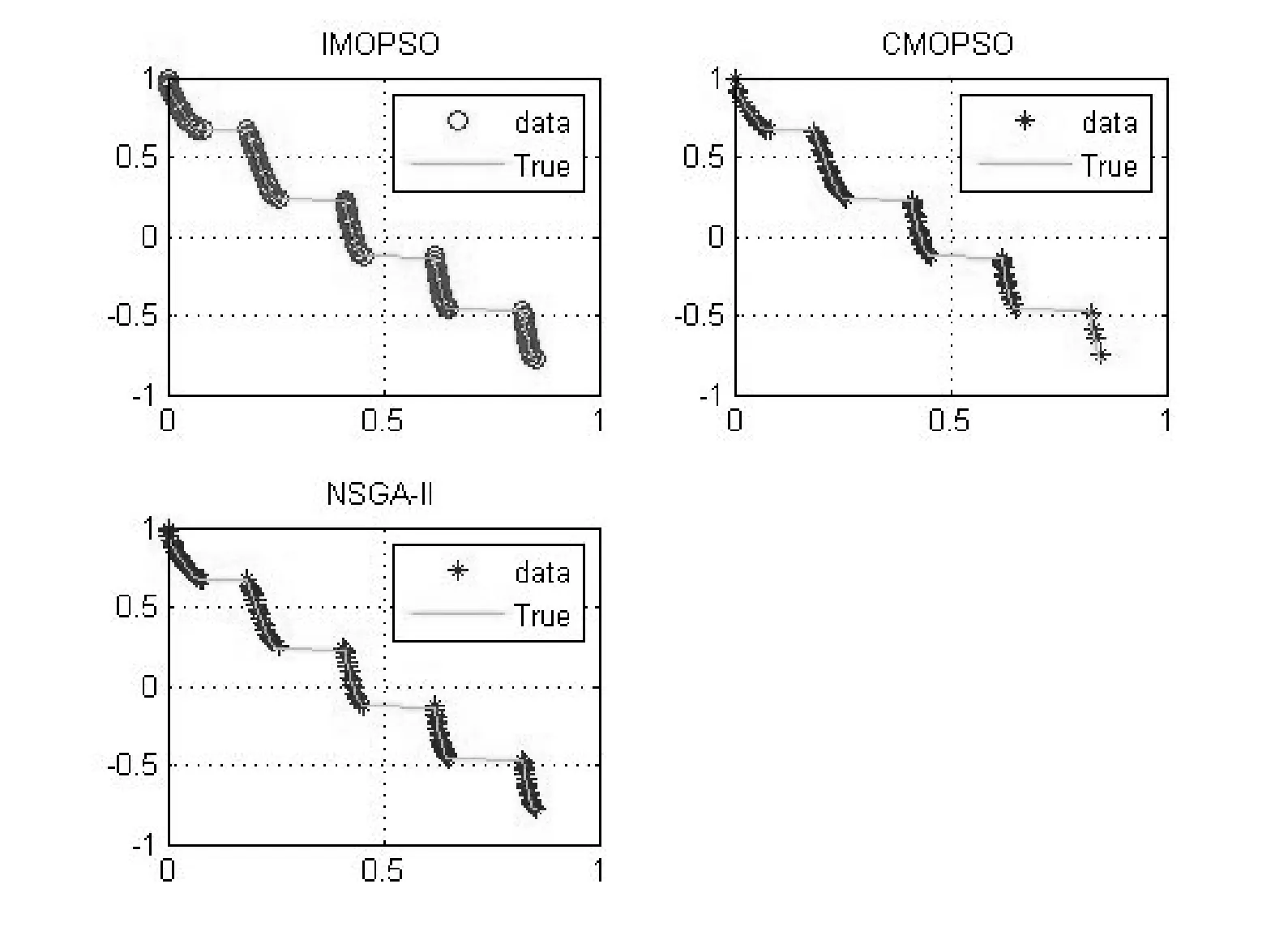
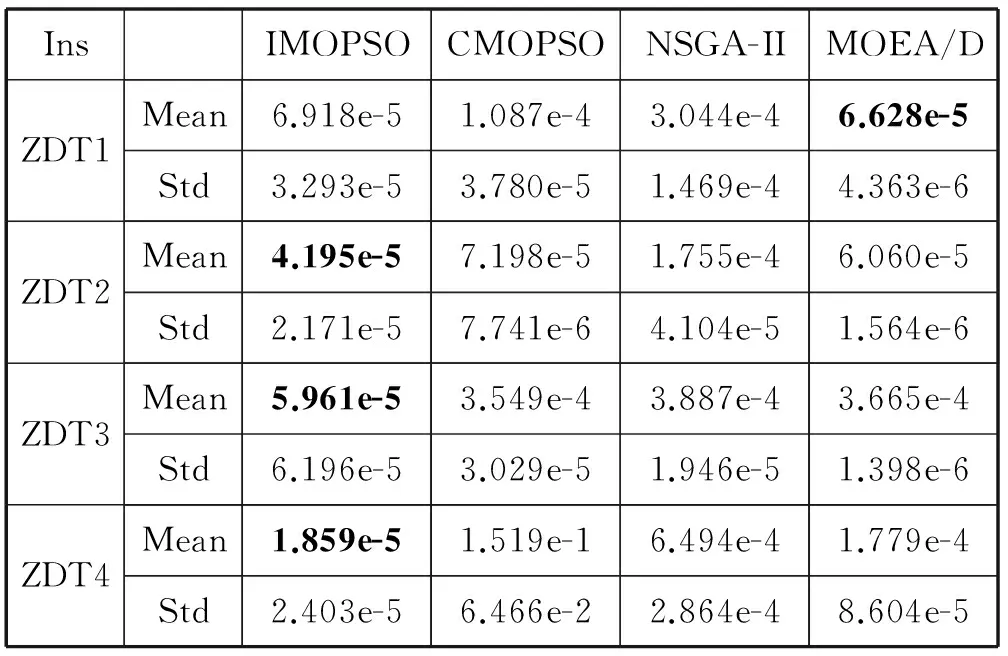
4) 若粒子迭代次数超过4次,则开始比较连续3代的适应度值,若其连续3代适应度值基本保持不变并且rand xid=wvid+c1rand(gbest-Tn) (2) 其中rand为0到1之间的随机数,gbest为从全局最优解集的前20%中随机挑选的解,Tn为粒子信息档案,n=r%5,r为当前迭代次数。 5) 若不满足4)中的条件则采用如下策略更新粒子的速度和位置(更新策略1)。 Vid=WVid+C1r1(pid-Xid)+C2r2(pgd-Xid) (3) Xid=Xid+Vid (4) 其中W为惯性权重,c1和c2为学习因子。 1.4 算法流程 本文采用的多目标粒子群优化算法的步骤为: 1) 根据1.1节的策略,初始化种群。 2) 计算各粒子的适应度值并根据支配关系形成非支配解集。 3) 更新外部档案集。 4) 按粒子间的拥挤距离对外部档案中的粒子进行降序排列,根据1.2节的策略进行档案维护。 5) 更新个体最优 ,若是第一代则直接将每个粒子初始位置设为,否则根据Pareto支配关系进行更新。 6) 从外部档案的前20%个非支配解集中随机选取一个全局最优位置。 7) 根据1.3节的策略来更新粒子的位置和速度。若粒子的速度vi>vmax则令vi=-vmax×rand;若粒子速度vi 8) 更新新一代的位置,若粒子的位置xi>xmax则令xi=xmax;若粒子位置xi 9) 根据当前迭代次数将各粒子存入不同的档案Tn中。 10) 检查是否达到最大迭代次数,如果达到,则终止程序;如果未达到,则继续从第二步开始循环。 改进的多目标粒子群优化算法流程图如图1所示。 图1 算法流程图 本文选取了几种对等的优化算法进行比较,本文采用世代距离GD来评价算法的收敛性,采用空间评价方法SP来评价解集的分布性。定义公式如下: (5) (6) GD值越小,说明算法的收敛性越好,SP值越小,说明得到的解的分布性越好。 本文测试函数为ZDT系列。该系列测试函数为双目标函数,ZDT1~4的Pareto前沿特征分别为二维连续凸函数,二维连续凹函数,不连续函数,凸函数。 各算法的种群规模均设为N=100,全局外部档案的最大容量均设为NN=100,所有算法的最大迭代次数Tmax=500,每种算法在所有的测试函数上均独立运行30次。 图2-图5为IMOPSO、CMOPSO、NSGA-II三种算法在四个测试函数上的仿真结果。 图2 三种算法对ZDT1函数求解的Pareto分布 图3 三种算法对ZDT2函数求解的Pareto分布 图4 三种算法对ZDT3函数求解的Pareto分布 图5 三种算法对ZDT4函数求解的Pareto分布 从图2-图5来看,IMOPSO算法与其他算法相比,无论是在求解数量、解集的逼近性以及分布性上都有较大的优越性。 表1列出了4个对等比较算法在4个测试问题上的GD性能指标, 这些值是同一算法在同一测试问题上独立运行30次的统计结果。其中比较算法结果数据来源于文献[6]。 表1 4种对等算法在4个测试实例上的GD性能对比结果 从表1可以看出,IMOPSO在4个测试问题中获得了3个最优的GD值,MOED/A算法获得一个最优的GD值。GD性能能够反映算法的收敛性,因此,从收敛角度来看,IMOPSO的表现较为突出。 表2给出了4种对等比较算法在4个多目标测试问题上的SP性能的对比结果。 表2 4种对等算法在4个测试实例上的SP性能对比结果 从表3可以看出,IMOPSO在4个测试函数上获得了4个最优的SP值。总体上来说,本文算法具有不错的SP性能。 综上所述,IMOPSO算法在所有测试函数中获得了最好的收敛性和多样性的折中效果,表明了本文改进之后的方法能够很好地均衡算法的进化过程,并在复杂多目标优化测试问题中取得了明显的效果。 本文通过结合文献[6-7]的优点,完善粒子的更新策略,提出了一种改进的多目标优化算法,并与一些算法进行了比较分析。通过对实验结果的分析可以看出,在求解多目标的问题上,改进后的算法相对于其他算法,能够更精确地收敛到标准测试函数的真实Pareto前端。并且,也能够维持好的解的分布性。 [1] 江勋林,郭坚毅,唐建,等.一种基于模糊学习子群的多目标粒子群算法[J].计算机应用研究,2011,28(12):4492-4494. [2] Agrawal S,Dashora Y,Tiwari M K,et al.Interactive Particle Swarm:A Pareto-Adaptive Metaheuristic to Multiobjective Optimization[J].IEEE Transactions on Systems,Man,and Cybernetics-Part A:Systems and Humans,2008,38(2):258-277. [3] Lin Q,Li J,Du Z,et al.A novel multi-objective particle swarm optimization with multiple search strategies[J].European Journal of Operational Research,2015,247(3):732-744. [4] Srivastava L,Singh H.Hybrid multi-swarm particle swarm optimisation based multi-objective reactive power dispatch[J].Generation Transmission & Distribution Iet,2015,9(8):727-739. [5] Zhang Y,Gong D W,Zhang W Q.Feature selection of unreliable data using an improved multi-objective PSO algorithm[J].Neurocomputing,2016,171(C):1281-1290. [6] 谢承旺,邹秀芬,夏学文,等.一种多策略融合的多目标粒子群优化算法[J].电子学报,2015,43(8):1538-1544. [7] 左一多.多目标优化问题的粒子群算法及其性能分析[D].北京:中国地质大学,2013. [8] Xu G,Yang Y Q,Liu B B,et al.An efficient hybrid multi-objective particle swarm optimization with a multi-objective dichotomy line search[J].Journal of Computational & Applied Mathematics,2015,280(C):310-326. [9] Clarke J,Jr M L.Multi-objective particle swarm optimization of binary geothermal power plants[J].Applied Energy,2015,138:302-314. [10] Liu H L,Gu F,Zhang Q.Decomposition of a Multiobjective Optimization Problem Into a Number of Simple Multiobjective Subproblems[J].IEEE Transactions on Evolutionary Computation,2014,18(3):450-455. ANIMPROVEDMULTI-OBJECTIVEPARTICLESWARMOPTIMIZATIONALGORITHM Xiang Tieming Wang Jiancheng* (InstituteofAntennaandMicrowaves,HangzhouDianziUniversity,Hangzhou310018,Zhejiang,China) In order to improve the ability to solve the problem of multi-objective optimization (MOPSO), an improved multi-objective particle swarm optimization algorithm (IMOPSO) is proposed. Using IMSPSO, initial population was produced by a uniformly random initialization approach, and non-dominated solutions were selected by fast control strategy to generate the external archive. By comparing the successive generations of particles, we could judge whether they felled into local optima and adopted different updating strategies. At the same time, a disturbance item was added to the particle’s updating. The experimental results show that the proposed algorithm significantly surpasses other algorithms in terms of GD(Generational Distance), SP(Spacing). External archive Uniform and random initialization Fast control strategy MOPSO Particle information archive TP181 A 10.3969/j.issn.1000-386x.2017.09.059 2016-11-09。项铁铭,副教授,主研领域:智能优化算法,多目标优化,现代天线设计。王建成,硕士生。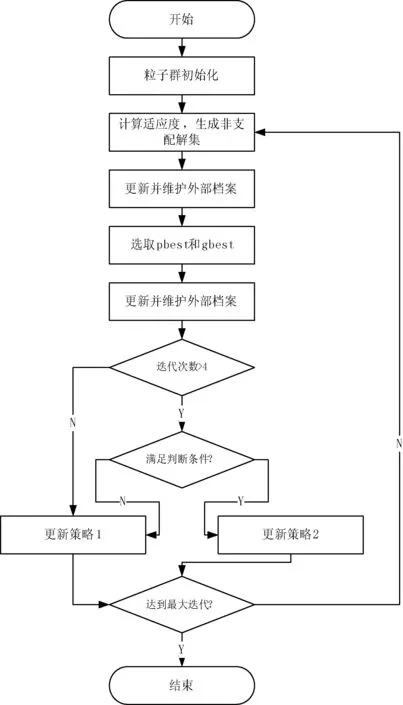
2 实验结果分析





3 结 语

