永磁直线同步电机的智能增量滑模控制

赵希梅，王晨光

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

永磁直线同步电机的智能增量滑模控制

赵希梅，王晨光

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

针对永磁直线同步电机直接驱动伺服系统的位置跟踪精度易受参数变化、外部扰动、端部效应等不确定性因素的影响，提出了一种将小波神经网络(wavelet neural network，WNN)和增量滑模控制器相结合的智能增量滑模控制方法。利用系统先前的状态信息和控制动作作为反馈量，同时选择饱和函数作为切换函数来设计增量滑模控制器，不仅削弱了抖振，而且提高了系统的跟踪性能；利用WNN实时观测和补偿参数变化和外部扰动等影响，并采用改进的粒子群优化算法在线调整WNN的学习率，对不确定因素进行实时估计。从理论上分析证明了此控制器可以保证系统收敛，提高了直线伺服系统的控制性能。通过系统实验，证明了所提出方案的有效性，与滑模控制(sliding mode control,SMC)相比，系统具有强鲁棒性和良好的位置跟踪精度，明显地削弱了抖振现象。

永磁直线同步电机；智能增量滑模控制；小波神经网络；改进粒子群优化算法；位置跟踪

0 引 言

直线电机近年来在结构和性能上有着突飞猛进的发展，使其可靠性和可控性逐渐增强，在工业领域中备受关注，作为执行部件逐渐被广泛地用于工业生产中的直接驱动设备上。在诸如半导体生产、精密机械、微电子装备生产、机器人控制、XY平台驱动等领域，需要在几十纳米到几米的直线行程上进行位置控制，直线运动系统高精度性能显得极其重要[1-2]。永磁直线同步电机(permanent magnet linear synchronous motor，PMLSM)与旋转电机相比，省去了间接机械传动装置，直接驱动负载，摩擦磨损只发生在直线轴承上；与其他直线电机相比，其磁场由永磁体产生，在动子和定子间产生磁通回路，散热更好，功率因数更高[3]。但是存在以下3个问题：对于模型的参数变化十分敏感，如动子质量和摩擦系数的变化；摩擦力成为影响系统精度的主要扰动，主要随着动子的速度而变化，且在低速时表现出严重的非线性；磁阻力严重影响系统的平稳运行，其产生原因是动子两端的端部效应，以及齿槽和永磁体相互作用产生的齿槽力[4]。因此在高精度控制系统中，对控制器的设计提出了更严格的要求，从而使系统对这些不确定性因素的影响具有强鲁棒性，增强系统高精度的控制性能。

为了解决上述问题，文献[5-6]采用了滑模控制(sliding mode control，SMC)方法。这是一种在不确定条件下控制高阶非线性复杂动态系统的方法，能有效减弱系统对不确定性等扰动的敏感度，并解决许多实际问题；但却存在明显的抖振现象。因此为了削弱抖振并提高系统的跟踪性能，在满足SMC的条件下，本文将系统先前的状态和控制动作作为反馈量，用饱和函数代替传统的符号函数，设计了增量滑模控制器，从理论上分析证明了系统的收敛性。

在增量滑模控制(incremental sliding mode control，ISMC)中，需要对不确定因素界限进行估计，无法精确补偿不确定性因素对系统控制精度的影响。为了改善这一问题，实时对扰动、参数变化等不确定性因素进行观测和补偿，提出了神经网络与ISMC结合的智能增量滑模控制(intelligent incremental sliding mode control，IISMC)方案。文献[7-8]设计了神经网络控制器，但一般的神经网络有时不可避免地使用过多的隐含层神经元结点，增大了计算负荷。同时由于参数随意设置，且输出因参数变化表现出高度非线性，很难保证系统总是收敛。因此为了克服这些缺点，采用小波神经网络(wavelet neural network，WNN)，它具有以下优点：小波函数具有空间局域性，学习能力更强；使用最少的隐含层节点数量就能实现最优逼近，学习算法使用最少的迭代次数就能实现收敛；能够实现输入输出的有效映射关系[9]。

为了对WNN的学习率进行在线调整，增强神经网络的性能，采用粒子群优化(particle swarm optimization，PSO)算法对学习率进行优化。PSO算法作为一种基于群体的最优化方法，在科学和工程领域逐渐发挥重要作用，可以高效地解决全局最优化问题[10]。PSO算法对粒子群的位置进行记忆，具有自适应的特征，不需要繁重的计算负荷，广泛地应用于控制、系统识别、图像处理等方面[11-12]。本文对PSO算法进行改进，对粒子最差的位置进行记忆，并作为算法的组成部分，提出了IPSO算法，增加了算法对最优解的探索能力。最后通过系统实验，证明了所提出的控制方法有效地削弱了抖振，降低了稳态误差，增强了系统鲁棒性。

1 PMLSM数学模型

在PMLSM控制系统分析中，通常假设仅包含初级磁动势的基波分量，因此可以使用d-q轴模型，其中将主磁极基波磁场轴线定义为d轴，将d轴逆时针旋转90°定义为q轴。根据磁场定向原理，取d轴的给定电流为0，为了设计方便，假设Ld=Lq=L，电磁推力Fe表示为

(1)

式中：iq为q轴电流；ψPM为永磁体产生的励磁磁链；τ为极距；Kt为电磁推力常数。

PMLSM的机械运动学方程表示为

(2)

式中：M为PMLSM的动子和动子所带负载总质量；B为粘滞摩擦系数；vm为动子线速度；FΣ为扰动，包括系统外部扰动、内部波动力和摩擦力等。

将式(1)代入式(2)可得

(3)

则运动方程为

(4)

实际系统中存在参数变化，所以式(4)可以写为

(5)

变为

(6)

2 PMLSM的IISMC系统设计

基于IISMC的PMLSM伺服控制系统框图如图1所示，其中智能增量滑模控制器如图中虚框所示，包括ISMC、WNN和IPSO等。

图1 基于IISMC的PMLSM伺服控制系统框图Fig.1 Block diagram of PMLSM servocontrol system based on IISMC

ti时刻智能增量滑模控制器的控制律设计为

u(ti)IISMC=u(ti)ISMC+u。

(7)

其中：u(ti)ISMC为ti时刻增量滑模控制律；u为WNN的输出。

2.1 增量滑模控制器的设计

为了削弱抖振并提高系统的跟踪性能，首先设计增量滑模控制器，先设计滑模切换函数，使系统状态在有限时间内趋近于滑模面，然后设计控制率，并满足滑模条件。令X(ti)为PMLSM的动子在ti时刻的实际位置，Xd(ti)为给定位置，定义ti时刻跟踪误差为

e(ti)=Xd(ti)-X(ti)。

(8)

滑模面设计为

(9)

其中λ为一个正常数。

控制律设计为：

u(ti)ISMC=u(ti-1)ISMC+ueq(ti)+uv(ti)。

(10)

ti=ti-1+Δt。

(11)

其中：u(ti-1)ISMC是上一时刻ti-1的控制动作；Δt为系统的步长；ueq(ti)为滑模等效控制部分；uV(ti)为滑模切换控制部分。ueq(ti)的表达式为

(12)

其中k为一正常数。

uv(ti)的表达式为

(13)

其中：β为一个正常数；sat(·)为饱和函数，表示为：

(14)

将式(10)、式(12)、式(13)代入式(6)可得

(15)

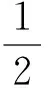
β|s(ti)|-μ|s(ti)|≤

-ks2(ti)-ρ|s(ti)|≤0。

(16)

(17)

2.2 WNN的设计

(18)

图2 三层WNN结构图Fig.2 Structure of a three-layer WNN

因此，ψ(x)满足母小波函数的条件。将ψ(x)进行伸缩和平移，得到

(19)

其中：m为平移参数；d为尺度参数。L2(R)表示一维函数f的向量空间，可测且平方可积，那么可以用小波网络以任意精度逼近任意的函数f∈L2(R)。

在小波层中，每个节点的输出如下：

(20)

ψj(x)=ψ(netj)。

(21)

其中：netj为小波层第j个节点；xi为WNN的第i个输出；mj、dj分别为第j个节点的平移参数和尺度参数；Ni为输入层节点个数。

在输出层，最终输出u等于所有输入信号经过计算变换后的加和，即

(22)

其中：wj为小波层和输出层的连接权值；Nw为小波层的节点数。

为了解决神经网络需要离线训练的缺点，本文设计了一种在线学习算法。学习算法可以描述为对梯度向量的计算，在梯度向量中，算法中的每个成分都可以定义成目标函数的微分，且包含WNN的各项参数，从而使目标函数的值取到最小。根据这一目的，采用反向误差传递学习规则，用梯度下降法对WNN参数进行在线学习。因此，将目标函数定义为

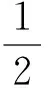
(23)

对于输出层而言，只有一个输出，传递的误差项可以写为

(24)

输出层的连接权值的变化量为

(25)

根据式(25)，输出层的权值通过下式进行更新，即

wj(k+1)=wj(k)+Δwj。

(26)

其中：ηw为权值的学习速率；k为迭代次数。在小波层中，因为小波层的所有权重都设为1，所以只有误差项需要计算和传递，小波层的误差项为

(27)

mj和dj的变化量分别为：

(28)

(29)

其中ηm和ηd分别为平移参数和伸缩参数的学习速率。根据式(28)、式(29)，平移参数和伸缩参数可以通过下式进行更新，即：

mj(k+1)=mj(k)+Δmj，

(30)

dj(k+1)=dj(k)+Δdj。

(31)

δ0中的系统Jacobian信息，即∂X/∂u，关系到控制对象输入的灵敏度，但因为系统的非线性动态特征，Jacobian信息很难被准确计算。为了解决这个问题，增加在线算法的计算速率，依据比例-微分控制的概念，采用以下自适应律代替误差项δ0为

(32)

2.3 IPSO的设计

为了提高所提出的WNN的在线学习能力，本文提出了IPSO算法，对WNN的学习率ηw、ηm和ηd进行在线调整。与传统的PSO算法不同，IPSO算法将认知部分分为两部分：一部分为最好经验部分，用来记住粒子先前所处的最好位置；另一部分为最坏经验部分，帮助粒子记忆先前访问过的最差位置，从而具备额外的识别能力。在计算新的速率时，利用最坏经验，新的速率更新公式为

(33)

(34)

为了计算适应度值，选择了一个合适的适应度函数FIT，函数为

(35)

IPSO算法优化步骤可分为以下6步：

1)初始化。需要设定的内容包括粒子的速度和位置的边界，粒子的数量，式(33)中的各参数的初始值，初始粒子群的位置。

2)初始粒子群的评价。根据式(35)计算整个初始粒子群的所有粒子的适应度值，通过最佳适应度值来确定整个群体的最好位置Gbest。

3)位置和速率的更新。根据式(33)、式(34)对位置和速率进行更新，检查粒子更新过的位置和速率是否超过设定界限，若超过，将其设为相应的界限值。

4)更新过的粒子群评价。与步骤2)相似，通过适应度函数计算适应度值，更新粒子的最好位置和最差位置，以及整个粒子群的最好位置。

5)终止条件的检查。检查是否满足预设的终止条件，预设的终止条件包括达到最大的迭代次数或满足适应度值的设置。如果没有满足终止条件，返回步骤3)重复计算；否则终止最优化进程。

6)输出结果。将整个粒子群的最优位置Gbest作为结果输出。

3 系统实验分析

本文搭建了基于DSP的PMLSM控制系统实验装置，对IISMC控制方法的有效性进行实验分析。系统采用位置环和电流环双闭环控制，位置控制器采用SMC、ISMC或IISMC方法，电流控制器采用PI控制，所选用的DSP型号为TMS320LF2812A，图3为基于DSP的PMLSM实验系统实物图。

图3 基于DSP的PMLSM实验系统实物图Fig.3 Photograph of PMLSM experiment systembased on DSP

PMLSM的参数如下：M=16.4 kg，B=8 N·s/m，Kt=50.7 N/A，R=2.1 Ω，ψf=0.09 Wb，τ=32 mm，Ld=Lq=41.4 mH。为了验证IISMC控制方法的有效性，分别对基于SMC、ISMC和IISMC的PMLSM控制系统进行实验对比研究。给系统输入两种不同的信号，其他条件相同，通过系统的响应来对比验证PMLSM控制系统跟踪性和鲁棒性。两种信号如下：①变周期和幅值的梯形波：开始时周期为0.9 s，幅值为2 mm，在2 s左右变成周期为0.7 s，幅值为1 mm，在3.5 s左右变成周期为1.1 s，幅值为1.75 mm。在2.5～3.5 s间突加FL=50 N的负载扰动。②变频率和幅值的正弦波：开始时频率为1 Hz，幅值为1 mm，2 s时变成频率为1.5 Hz，幅值为1.5 mm，4 s时变成频率为1.25 Hz，幅值为1.25 mm。在2.5～3.5 s间突加FL=50 N的负载扰动。

为了使系统工作在最优状态下，对控制系统进行不断调试，从而得到相关参数。基于SMC的PMLSM控制系统参数选择如下：λ=50，β=4.5，φ=0.000 25。基于ISMC和IISMC的PMLSM控制系统参数选择如下：λ=70，φ=60，k=0.1，β=3。为了提高控制系统的性能，对系统进行实验时增加了一个性能测试环节，用幅值1 mm、频率为1 Hz的正弦波对WNN进行训练，初始时WNN各项参数随机设置，在1 s的循环在线训练后，能获得精确的跟踪性能，WNN的所有参数在1 s训练后被记忆下来，作为正式实验时WNN参数的初始值。图4为1 s在线训练时位置误差曲线。因此，得到的初始值如下：w1=0.13，w2=0.35，w3=0.24，m1=0.25，m2=0.27，m3=0.22，d1=0.31，d2=0.24，d3=0.17。IPSO算法参数设置为：P=30，d=3，k=100，c1=1.4，c2=1.8，c3=3。

图4 1 s在线训练时位置误差曲线Fig.4 Position error curve of online training in 1 s

位置输入信号①的曲线如图5(a)所示，图5(b)、(c)、(d)分别为当系统输入为信号①时，SMC、ISMC和IISMC系统的位置误差曲线。通过观察可发现，SMC系统的跟踪误差在-10～15 μm之间，2.5 s时加入扰动后位置误差上升到接近20 μm。ISMC系统的位置误差在-2.5～5 μm之间。IISMC系统的位置误差在-0.5～2 μm之间，所以跟踪误差最小，鲁棒性最好。在同一时间段内放大位置误差曲线，SMC系统的抖振幅度为1.25 μm，ISMC系统的抖振幅度为0.4 μm，IISMC系统的抖振幅度为0.05 μm，所以IISMC系统明显削弱了抖振现象。

图5 输入为梯形信号时系统的位置曲线Fig.5 Position curves of systems for trapezoid signal input

位置输入信号②的曲线如图6(a)所示，图6(b)、(c)分别为当系统输入为信号②时，SMC和ISMC系统，SMC和IISMC系统的位置误差曲线。可以看出，SMC系统的位置误差在4～5 μm间振动，最高达到8 μm，2.5 s时加入扰动，误差出现了明显的波动。ISMC系统的位置误差最高达到1.5 μm。IISMC系统的位置误差最高只有0.5 μm，明显减小了跟踪误差，突加负载时表现出很强的鲁棒性。在同一时间段内放大位置误差曲线，SMC系统的抖振幅度为1.5 μm，ISMC系统的抖振幅度为0.8 μm，IISMC系统的抖振幅度为0.2 μm，所以IISMC系统明显削弱了抖振现象。

图6 输入为正弦信号时系统的位置曲线Fig.6 Position curves of systems for sinusoid signal input

4 结 论

PMLSM伺服系统的IISMC方法与传统的SMC方法不同，IISMC的设计考虑了先前的系统状态和先前的控制动作，并且采用了WNN，设计了在线学习算法，实时观测和补偿扰动，对不确定项进行在线估计，并利用IPSO算法，对学习算法中的学习率进行实时调整。通过理论和实验分析得出，所提出的方案有效可行，基于IISMC的PMLSM伺服系统有效地削弱了SMC方法的抖振现象，使系统既具有快速跟踪性能，又具有较强的鲁棒性能，明显改善了系统的控制性能，大大减小了位置误差。

[1] HAMA T,SATO K.High-speed and high-precision tracking control of ultrahigh-acceleration moving permanent magnet linear synchronous motor[J].Precision Engineering,2015,40:151.

[2] MAO Jingfeng,WU Guoqing,WU Aihua,et al.Nonlinear decoupling sliding mode control of permanent magnet linear synchronous motor based on α-th order inverse system method[J].Procedia Engineering,2011,15:561.

[3] MOHAMMADPOUR A,PARSA L.Optimal design and prototyping of a five-phase direct-drive permanent magnet linear motor[C]// International Symposium on Power Electronics,Electrical Drives,Automation and Motion，Italia.2014:449-454.

[4] CHO K,KIM J,CHOI S B,et al.A high-precision motion control based on a periodic adaptive disturbance observer in a PMLSM[J].Transactions on Mechatronics,2015,20(5):2158.

[5] BARAMBONES O,ALKORTA P.A robust vector control for induction motor drives with an adaptive sliding-mode control law[J].Journal of the Franklin Institute,2011,348(2):300.

[6] HACIOGLU Y,ARSLAN Y Z,YAGIZ N.MIMO fuzzy sliding mode controlled dual arm robot in load transportation[J].Journal of the Franklin Institute,2011,348(8):1886.

[7] 秦斌，周浩，杜康,等.基于RBF网络的风电机组变桨距滑模控制[J].电工技术学报，2013，28(5)：37.QIN Bin,ZHOU Hao,DU Kang,et al.Sliding mode control of pitch angle based on RBF neural-network[J].Transactions of China Electrotechnical Society,2013,28(5):37.

[8] LIN Chuankai.Radial basis function neural network-based adaptive critic control of induction motors[J].Applied Soft Computing,2011,11(3):3066.

[9] LIN C M,HSUEH C S,CHEN C H.Robust adaptive backstepping control for a class of nonlinear systems using recurrent wavelet neural network[J].Neurocomputing,2014,142:372.

[10] CLERC M,KENNEDY J.The particle swarm-explosion,stability,and convergence in a multidimensional comple xspace[J].Evolutionary Computation,2002,6(1):58.

[11] SMAIL M K,BOUCHEKARA H,PICHON L,et al.Diagnosis of wiring networks using particle swarm optimization and genetical gorithms[J].Computers & Electrical Engineering,2014,40(7):2236.

[12] BEDI P,BANSAL R,SEHGAL P.Using PSO in a spatial domain based image hiding scheme with distortion tolerance[J].Computers & Electrical Engineering,2013,39(2):640.

(编辑：刘琳琳)

Intelligentincrementalslidingmodecontrolforpermanentmagnetlinearsynchronousmotor

ZHAO Xi-mei，WANG Chen-guang

(School of Electrical Engineering,Shenyang University of Technology,Shenyang 110870,China)

Intelligent incremental sliding mode control (IISMC) method combining wavelet neural network (WNN) with incremental sliding mode controller was proposed for permanent magnet linear synchronous motor (PMLSM) direct-drive servo system of which the precision of position tracking is vulnerable to the influence of the uncertainties,such as parameter variations,external disturbances,inherent end effect and so on.First,incremental sliding mode controller was designed by utilizing previous state information and control action,and adopting the saturated function as the switching function.The proposed controller achieves high precision tracking and chattering reduction.Then,to observe and compensate the influence such as parameter variation and external disturbances,while estimating uncertain parameter in real time,WNN was investigated,which used an improved particle swarm optimization (IPSO) algorithm to adjust the learning rate online.In theory,the proposed controller is proved to guarantee the convergence of the system tracking error.Finally,system experimental results confirm effectiveness of the proposed method.Compared with the sliding mode control (SMC),the system has accurate position tracking performance and strong robustness,meanwhile,the chattering is obviously reduced.

permanent magnet linear synchronous motors; intelligent incremental sliding mode control; wavelet neural network; improved particle swarm optimization; position tracking

10.15938/j.emc.2017.09.007

TM 315

:A

:1007-449X(2017)09-0047-08

2016-04-08

国家自然科学基金(51175349)；辽宁省自然科学基金(20170540677)

赵希梅(1979—)，女，博士，副教授，研究方向为直线伺服、数控、鲁棒控制等；王晨光(1990—)，男，硕士研究生，研究方向为直线伺服、智能控制。

赵希梅