一种时域电磁仿真终止判断的新方法

张刚，于洪海，王立欣

(1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001；2.国网黑龙江省电力有限公司检修公司，黑龙江 哈尔滨 150090)

一种时域电磁仿真终止判断的新方法

张刚1，于洪海2，王立欣1

(1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001；2.国网黑龙江省电力有限公司检修公司，黑龙江 哈尔滨 150090)

时域电磁仿真方法在求解谐振结构响应时能量耗散慢，为了获取理想的频域结果，需要大量的仿真步数。采用矢量拟合方法对频域仿真结果根据已有初始频点进行预测，同时采用特征选择验证方法对相邻两次拟合结果进行相似度比对，使用特征选择验证方法的输出结果作为仿真终止的判据，并讨论了对比步长与收敛判据之间的关系。使用开缝金属箱体的屏蔽效能仿真算例验证判据的有效性，并与传统基于能量衰减的仿真终止判据进行性能对比。实验表明，提出的方法在保证仿真精度的同时可以节省谐振结构的仿真时间，说明使用矢量拟合和特征选择验证方法进行谐振结构的时域仿真收敛判断是有效可行的。

时域方法；仿真终止时间；矢量拟合 ；特征选择验证

0 引 言

由于电磁场的时域求解算法运行一次就可得到结构的宽频特性，在求解开域问题及电大问题时得到了广泛应用。因此，时域有限差分方法、时域有限元法以及时域矩量法等时域求解方法受到越来越多的重视[1-2]。但是，应用时域算法求解一些谐振或高Q值的无源结构时，为获取较为理想的频域仿真结果，往往需要很长的仿真时间来使得能量耗散至预设的精确度；因此，如何提高这种情况下的仿真速度成为时域求解算法实际应用中面临的一个困难。

时域仿真的一个很重要的优势在于其结果可以通过傅里叶变换转化为宽频带的频域结果。对于谐振或高Q值的无源结构而言，在能量衰减至零值前停止仿真往往使得频域结果与实测结果相差甚远。这主要是由于在傅里叶变换时，为了获取全部所关心的频点，商业仿真软件采取的解决方案是对过早截断的时域结果进行补零从而造成频域结果出现纹波[3]。

早期解决这一问题的方法是通过对时域仿真结果进行拟合来节省仿真时间，通过少量时域仿真数据来预测之后的仿真结果从而避免简单的数据补零带来的误差问题[4]。主要方法有自回归方法[5]、广义函数束方法[6]、神经网络模型法[7]和Prony方法[8]等；但使用上述方法进行数据外推时，容易受到信号噪声的影响，基于染噪数据建立的数据模型容易使外推数据偏置真值[9]。文献[10]提出改进的矩阵束方法(modified matrix pencil)，其基本原理是利用若干衰减指数方程作为基来构造谐振结构的时域仿真结果，克服噪声数据对估计结果的影响。近些年，随着矢量拟合技术[11-14]的出现，使得通过对频域数据的拟合来预测模型的传输函数成为可能。时域仿真所对应的频域结果一般通过傅里叶变换获得，理论上，频谱带宽取决于时域采样频率(仿真的时间步长)，频率采样间隔取决于时域数据的时间长度。通过首先对部分时域仿真结果进行变换可得到整个频谱的概貌，在此间基础上通过矢量拟合技术来获得详细的频谱信息；因此，本文将尝试从频域角度对仿真数据进行预测，从而缩短时域仿真时间。

使用数据拟合技术来加速时域电磁仿真的过程中，需要解决的另一问题是如何合理地确定拟合所需的时域数据的长度，即仿真终止判据的设定问题。现有的研究均是以真值结果作为参考数据进行方法讨论，而在实际的仿真过程中，真值是不可获取的。本文采用IEEE 1597.1标准中的特征选择验证方法(FSV)[15-17]对预测后的频域结果随着仿真时间增加的变化情况进行比对，从而判断仿真是否进入谐振状态或稳定状态并终止仿真。特征选择验证方法是近年来出现的一种电磁兼容仿真结果有效性判断的新方法，其特点是可以模拟专家对电磁仿真数据与参考数据之间差异的判读并给出自然语言描述的相似度，从而确定仿真结果的有效性。将这一判据引入时域电磁仿真终止的判断可以大大提高方法的适用性。

本文首先介绍了矢量拟合方法及特征选择验证方法的相关内容。随后，讨论了应用上述两种方法进行时域仿真终止判断的基本步骤。最后，通过分析一个典型的开缝金属箱体屏蔽效能的仿真过程来说明本方法的实际应用效果。

1 矢量拟合方法

矢量拟合方法在EMC分析中是一种比较新的拟合工具。它可以根据所研究对象的测量或仿真的频率响应，得到其传输函数的有理近似。传输函数的极点-留数形式为

(1)

其中:cn为留数,an为极点，二者可为复数或实数；d和e为实数；N为近似阶数。

对传输函数的估计归结为对式(1)中参数的估算。由于极点出现在分母上，问题演变为未知量的非线性问题；而矢量匹配法通过首先定位极点，将式(1)转变为未知量cn、d和e的线性问题，最终通过线性最小二乘方程计算出未知量。矢量拟合方法的优势在于即使是在很宽的频率范围内对高阶的有理函数进行拟合，也能得到好的结果[9]。

矢量拟合方法中初始极点的选择对拟合精确度有很大的影响。如果初始极点为实数极点，则即使是线性问题，式(1)在求解过程中也可能出现方程病态问题，导致拟合误差增大[9]。初始极点和实际极点差距过大亦会影响拟合精确度及速度。解决上述问题主要通过以下2种途径：

1) 如果f(s)是比较光滑的函数，采用实极点匹配即可获得精确的结果，极点随频率线性或对数化分布；但对于具有多谐振峰的函数，则应使用复极点，即

其中α=β/100。β线性或对数分布在所求解的频率范围内。

2)初始极点与实际极点相差过大的问题，可以通过初始极点的重新定位与用新极点作为迭代程序中的初始极点来解决。

综上，在仿真过程中随着仿真步数的增加，更多的频点参与式(1)中未知量的估计，从而使得近似传输函数的描述更加接近于真实情况。本文正是基于此特性，引入特征选择验证方法来比较不同仿真步数所得到的拟合结果之间的差异，根据这种差异的变化来决定是否终止仿真。

2 特征选择验证方法

特征选择验证方法(feature selective validation，FSV)由英国学者A.J.M.Martin提出，目的是使用数值的方法来模拟专家目视评估数据相似度的过程，从而定性或定量地给出与专家相似的对仿真有效性的判断。目前该方法已经成为IEEE Std 1597.1[18]及其实用手册IEEE Std 1597.2[19]中的推荐算法，并且对方法本身的改进及其应用的探讨也在不断深入[20-22]。

FSV方法主要思想如图1所示，通过傅里叶变换及其逆变换，将待比较数据分解为趋势数据(直流和低频分量)和特性数据(高频分量)。直流和低频部分的比对给出了两组数据的趋势差异量(ADM)，低频和高频部分的导数的分析比对给出了其特性差异量(FDM)，以上的两个指标合成全局差异量(GDM)来综合评估数据的可信度，其表达式为

(2)

图1 FSV方法的基本思想Fig.1 FSV method

FSV方法的每一个指标都具有多种表现形式：点对点的结果(ADMi、FDMi、GDMi)可以指示每个数据点处对应的差异；点对点结果的均值构成单值结果(ADM tot、FDM tot、GDM tot)用来指示每一个指标的总体值，每一个定量的单值结果均可以对应如表1所示的定性结果，方便使用者对数据有效性的理解。

表1 FSV评估方法的等级划分Table 1 FSV interpretation scale

3 仿真终止判断方法流程

使用矢量拟合方法及FSV方法进行仿真终止判断的流程如图2所示，主要包含以下几个步骤：

1)应用时域算法对所建模型进行计算，首先计算时间T0内的时域响应并记录仿真结果。然后再继续计算ΔT时间内的响应，记录。ΔT为1个仿真终止判断检验步长。

2)对记录的有限长时域仿真结果f(tk)进行离散傅里叶变换(DFT)，获取其频域响应F(ωk)，如下式所示：

(3)

其中，ωk=k/(NnΔt)，Nn为仿真获取的时域数据的长度。由于仿真得到的响应时间长度的限制，变换后的频点ωk及其响应F(ωk)为所求频点ω及其响应F(ω)的子集。

3)使用矢量拟合方法对频域结果F(ωk)进行拟合，即

(4)

获取极点—留数形式的有理方程的参数，进而可以得到未知频点的响应。

使用矢量拟合技术可以获取因仿真时间过短而缺失的频点，而不是通过对时域数据补零后再进行傅里叶变换来实现，避免了由“截断效应”带来的频域结果的纹波。

4)使用FSV方法比较相邻两次拟合的结果RFn(ω)和RFn-1(ω)在所求频点ω上的差异，并用其全局结果GDMtot值定义仿真终止判据GDMn，门限值ε的定性描述可根据表1定义。

如果比较结果GDMn大于上一次比较结果GDMn-1，则认为有新的频域成分出现，仿真未进入稳定状态，则继续进行仿真。否则，继续检验比对结果是否达到预定的限值ε(即相邻两次仿真结果的差异度预设值)，即

GDMn=FSV{RFn(ω),RFn-1(ω)}<ε。

(5)

若满足则终止仿真，若不满足则继续计算下一个ΔT时间内的响应。

图2 方法的基本思想 Fig.2 Flow chart of basic idea

4 算例及结果分析

使用时域方法计算如图3所示的带有缝隙的金属箱体的在频率为0.2～1.2 GHz范围内的屏蔽效能。采用商用电磁仿真软件CST的时域求解器来计算该模型，这一软件是目前时域电磁仿真中的主流解决方案，其对时域仿真终止判据的设定具有代表意义。从算例的选择上，选取了开缝金属箱体作为建模对象，主要是考虑这一类结构存在明显的谐振问题，是目前时域电磁仿真中比较难以处理(耗时、收敛困难)的结构，具有一定的代表性。

箱体尺寸结构如图3所示，箱体壁厚2 mm，箱体材料为理想导体。选用CST软件的瞬态求解器求解箱体内中心点的电场强度，进而求取箱体的屏蔽效能。屏蔽效能(shielding effectiveness，SE)[21]定义为

(6)

图3 开缝箱体模型 Fig.3 Size of metal box with aperture

这一算例是很典型的电磁兼容仿真问题，同时又是一个谐振结构，入射电磁波能量在箱体内耗散缓慢。传统仿真使用能量的耗散程度来进行仿真的终止判断，因此在计算此类模型时往往需要很长时间才能达到预定的精确度要求。基于能量衰减的仿真终止判据定义为

(7)

其中：EMax为仿真激励函数所能达到的最大能量值；ELeft为随着时间增长所剩余的能量。

图4为箱体中心的电场在终止判据为-60 dB时的仿真结果，仿真步数138 301步，仿真电场时长16.8 μs。从图中可以看出，此时时域仿真结果依然未衰减到零值。因而，通过傅里叶变换获取的频域仿真结果(图5所示)出现由于截断效应带来的纹波。当将终止判据设定为-80 dB时，仿真电场时长增加至38 μs，仿真步数达到314 701步时，频域仿真结果变得平滑，但此时耗费的计算时间和资源过多。图6为依靠能量耗散进行收敛判断的精度曲线。从图中可以看出，能量达到最大值后开始缓慢衰减，进而使得达到预设精度的仿真时间变长。

图4 仿真精度设为-60 dB时的仿真结果Fig.4 Simulated results with accuracy -60 dB

图5 不同仿真终止判据下仿真结果的对比Fig.5 Comparison of simulated results for different values of stopping criterion

图6 基于能量耗散的仿真精度变化曲线Fig.6 Change of accuracy based on energy

使用本文提出的方法，相邻两次仿真结果的比对间隔ΔT分别为500和1 000个脉冲长度(根据所求频率范围生成的高斯脉冲激励的长度)。终止判据设定为0.1(Excellent)，即相邻两次仿真结果比较不出现明显变化(差异度小于0.1)时即可视为仿真进入稳态，停止仿真。图7为使用矢量拟合方法获取的频域拟合曲线及所使用的待拟合数据，图中所示的小于0.001的拟合误差说明使用式(1)拟合得到的曲线能够很好的表示仿真结果。

图7 矢量拟合效果Fig.7 Fitted result and deviation

图8 不同检测步长下的GDMn变化曲线 (ε=0.1)Fig.8 Change of GDMn for different test steps(ε=0.1)

仿真收敛曲线如图8所示，在相同终止判据(ε=0.1)要求下，检验步长为500个脉冲长度时的收敛速度快于检验步长为1 000个脉冲长度。这是由于随着检验步长的增加，相邻两次结果的差异变大，在相同预设判据阈值下仿真所需要的时间更长。

由于本文提出的方法与传统方法在终止判据的定义上完全不同，为了检验本文所提出的方法的性能，对比了相同仿真时间内两种终止判据及数据处理方法所得到结果与可信数据之间的差异。采用传统能量终止判据设置为-80 dB的仿真结果作为可信结果，使用FSV方法对不同设置下的仿真结果进行了对比。

对不同的终止判据ε和检验步长下的最终仿真结果进行了如表2所示的分析。从表中可以看出，在同样的仿真时间长度下，与参考结果相比，本文提出的方法比传统方法仿真数据准确性在步长为500个脉冲长度时提高一个评价等级(Fair到Good)，而在检测步长设为1 000个脉冲长度时则可以提高两个等级(Fair到Very Good)。此外，对于本文提出的方法，在ε值一定的情况下，检测步长越长，仿真结果的准确性越高；在检测步长一定的条件下，ε值越高，仿真结果的准确性越高，反之亦然。

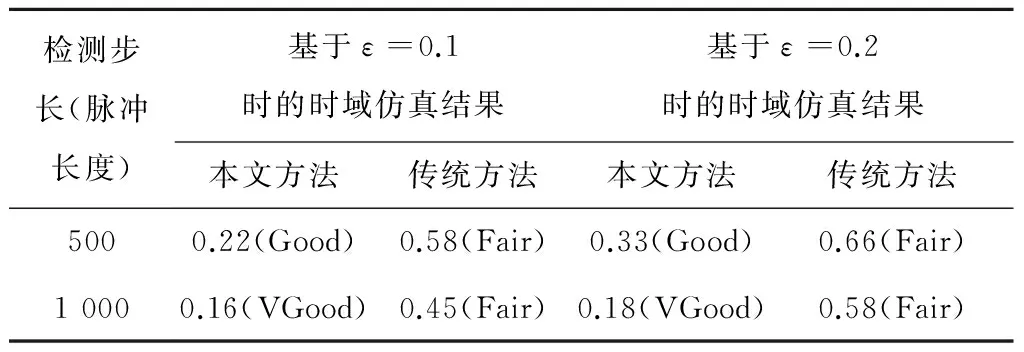
表2 不同ε值及检验步长下仿真结果可信度对比Table 2 Comparison of FSV results for different ε and different stopping criterion

表3 不同ε值下的仿真的电场响应时长对比Table 3 Comparison of simulated electric field time for different ε μs

结合表3所示的不同设置下的仿真电场时间，在ε设置为0.2，终止检测步长设置为500个脉冲长度时，仿真得到的电场响应时长仅为14.1μs，而此时的准确度则达到0.33(Good)。对比传统方法，其在电场响应时长达到31.7μs时(ε值设为0.1，检测步长1 000个脉冲长度)，结果准确度仅达到0.45(Fair)。可以得出结论，在占用相同的计算资源的条件下，使用矢量拟合和FSV方法进行仿真终止判断比基于傅里叶变换和能量衰减的终止判断方法准确性更高。

图9为ε值设为0.2，检测步长设置为500个脉冲长度时不同方法的仿真结果对比。采用式(7)所示仿真判据为-80 dB时的仿真结果作为参考数据。可以看出，使用本文提出的仿真终止判断方法后，所得出的结果与真实值之间的差异较小，且仿真结果较为平滑，在保证仿真准确度的条件下避免了时间和计算资源的浪费；而使用传统方法得到的仿真结果纹波较多，与参考值差异较大。

由以上分析，本文提出的方法可以在不增加仿真时间的前提下提高仿真结果的准确性，在谐振结构的时域仿真中节省计算资源和计算时间。还应注意到，由于引入了FSV方法的结果来定义仿真终止判据ε，根据表1，用户可以明确地理解其定性含义。

图9 不同仿真终止判断方法的仿真结果对比Fig.9 Comparison of simulated results for different stopping criterions

由于FSV方法的作用是对比2组数据之间的相似度，本文中仿真终止判据是相邻两次仿真(相差1个收敛检测步长)结果得出的矢量拟合数据之间的差异度。因此仿真终止判据主要由2个参数决定，FSV结果阈值ε和收敛检测步长，二者之间呈现负相关，即收敛检测步长越大，阈值ε越小，得到的而仿真结果可信度越大，而相应的仿真时间也越长。由于FSV的差异度可以使用自然语言描述，所以将其作为终止判据更容易被使用者所接受和理解；因此，在实际的应用中，可以固定收敛检测步长的值，而将ε值的设定对用户开放。当阈值ε设置过大，确实会带来不收敛的情况，防止出现此类情况的方法是采用自然语言描述来代替ε值，如引入表1所示的对应关系，避免不合理的阈值设置。

5 结 论

本文提出将矢量拟合技术和FSV方法结合进行时域仿真终止的判断。相比较于传统的基于能量耗散的仿真终止判断，本文方法的提出具有2个主要的优点。首先，将定性意义和定量指标结合，使得使用者对仿真终止条件有更好理解。另外，对于谐振结构的时域仿真，借助于本文提出的方法可以通过在频域内对结果进行拟合而缩短仿真时间并提高仿真结果准确性。在实际应用中，可将检测步长设为定值，通过改变使用自然语言定义的收敛判断阈值ε来定义模型仿真精度。

[1] 严登俊,朱长江,李伟.有限公式电磁场数值计算理论与性能[J].电机与控制学报,2007,11(1):12.YAN Dengjun,ZHU Changjiang,LI Wei.Theory and performance of finite formulation method for electromagnetic field numerical calculation[J],Electric Machines and Control,2007,11(1):12.

[2] 黄志鹏,李忠华,郑欢.复合电介质介电性能有限元仿真[J].电机与控制学报,2011,15(8):13.HUANG Zhipeng,LI Zhonghua,ZHENG Huan.FEM simulation for dielectric properties of composite material[J].Electric Machines and Control,2011,15(8):13.

[3] DESCHRIJVER D,PISSOORT D,DHAENE T.Adaptive stopping criterion for fast time domain characterization of microwave components[J].IEEE Microwave and Wireless Components Letters,2009,19(12):765.

[4] JANDHYALA V,MICHIELSSEN E,MITTRA R.FDTD signal extrapolation using the forward-backward autoregressive (AR) model[J].IEEE Microwave and Guided Wave Letters,1994,4(6):163.

[5] CHEN J,WU C,WU K L,et al.Combining an autoregressive (AR) model with the FD-TD algorithm for improved computational efficiency[J].IEEE Microwave Theory and Techniques Society Int.Dig.,1993,2:749.

[6] HUA Y,SARKAR T K.Generalized pencil-of-function method for extracting poles of an EM system from its transient response[J].IEEE Transactions on Antennas and Propagation,1989,37(2):229.

[7] WU C,NAVARRO E A,NAVASQUILLO J,et al.FDTD signal extrapolation using a finite impulse response neural network model[J].Microwave and Optical Technology Letters,1999,21(5):325.

[8] KO W L,MITTRA R.A combination of FD-TD and Prony's methods for analyzing microwave integrated circuits[J].IEEE Transaction on Microwave Theory Technology,1991,3:1742.

[9] CUI Yaozhong,WEI Guanghui,WANG Song,et al.Fast analysis of reverberation chamber using FDTD and improved matrix pencil method[J].IEEE Antennas and Wireless Propagation Letters,2013,12:845.

[10] CUI Yaozhong,WEI Guanghui,WANG Song,et al.Fast analysis of reverberation chamber using FDTD method and matrix pencil method with new criterion for determining the number of exponentially damped sinusoids[J].IEEE Transactions on Electromagnetic Compatibility,2014,56(3):510.

[11] GUSTAVSEN B,SEMLYEN A.Rational approximation of frequency domain responses by vector fitting[J].IEEE Transactions on Power Delivery,1999,14(3):1052.

[12] HENDRICKX W,DHAENE T.A discussion of “Rational approximation of frequency domain responses by vector fitting”[J].IEEE Transactions on Power Systems,2006,21(1):441.

[13] GUSTAVSEN B,SEMLYEN A.Simulation of transmission line transients using vector fitting and modal decomposition[J].IEEE Trans.Power Del.1998,13(2):605.

[14] 张重远,徐志钮,律方成,等.电压互感器的高频无源电路模型[J].电工技术学报,2012,27(04):77.ZHANG Zhongyuan,XU Zhiniu,LU Fangcheng,et al.High frequency passivity circuit model of potential transformers[J].Transactions of China Electrotechnical Society,2012,27(04):77.

[15] DUFFY AP,MARTIN AJM,Orlandi A,et al.Feature selective validation (FSV) for validation of computational electromagnetics (CEM).Part I - The FSV method[J].IEEE Transactions on Electromagnetic,2006,48(3):449.

[16] ORLANDI A,DUFFY AP,ARCHAMBEAULT B，et al.Feature selective validation (FSV) for validation of computational electromagnetics (CEM).Part II-Assessment of FSV performance[J].IEEE Transactions on EMC,2006,48(3):460.

[17] A J M Martin,Quantitative data validation[D].Leicester:De Montfort University,1999.

[18] IEEE STD 1597.1-2008,IEEE Standard for Validation of Computational Electromagnetics Computer Modeling and Simulations[S].

[19] IEEE Std 1597.2-2010,IEEE Recommended Practice for Validation of Computational Electromagnetics Computer Modeling and Simulations[S].

[20] Duffy A,Orlandi A,and Sasse H.Offset difference measure enhancement for the feature-selective validation method[J].IEEE Transactions on Electromagnetic Compatibility,2008,50:413.

[21] ORLANDI A,ANTONINI G,RITOTA C,et al.Enhancing Feature Selective Validation (FSV) interpretation of EMC/SI results with grade-spread[C]//IEEE International Symposium on Electromagnetic Compatibility,362.

[22] 张刚,王立欣,刘超.高频多导体串扰的三维全波简化算法及其有效性评估[J].电工技术学报,2012,27(9):140.ZHANG Gang,WANGLixin,LIU Chao.A multiconductor reduction 3D full-wave method for high frequency crosstalk problem and its validation[J].Transactions of China Electrotechnical Society,2012,27(9):140.

[23] C R Paul.电磁兼容导论[M].闻映红等译.北京:人民邮电出版社,2007.

(编辑：张 楠)

Stoppingcriterionoftimedomainelectromagneticsimulation

ZHANG Gang1，YU Hong-hai2，WANG Li-xin1

(1.School of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150001,China;2.State Grid Heilongjiang Electric Power Co.,Ltd.,Maintenance Company,Harbin 150090,China)

Because of the slow decay of energy,program has to be run for a large number of simulation steps before getting the response of resonant structures in the application of time domain electromagnetic solvers.To solve this problem,the Vector Fitting technology was employed to predict the frequency behavior based on a reasonable number of initial time steps.Then the predicted results were compared with the results from the previous iteration steps by the Feature Selective Validation method.Output of Feature Selective Validation method was adopted as the stopping criterion of the simulation.Also,relationship between the length of comparing step and stopping criterion was discussed.Calculation of the shielding effectiveness of a metal box with aperture was adopted to validate the proposed stopping criterion that is compared with traditional criterion based on energy attenuation.It is demonstrated that proposed stopping criterion can save simulation time that is consumed to reach the predefined accuracy.Therefore,it is useful to apply the vector fitting and feature selective validation method to the stopping criterion of time domain electromagnetic solvers for the simulation of resonant structures.

time domain simulation; stopping criterion; vector fitting; feature selective validation method

10.15938/j.emc.2017.09.003

TM 15

:A

:1007-449X(2017)09-0015-07

2017-03-24

国家自然科学基金(51477036)；中国博士后科学基金(152757)

张 刚(1984—)，男，博士，研究方向为电磁兼容及仿真技术；于洪海(1978—)，男，高级工程师，研究方向为电气设备故障诊断；王立欣(1966—)，男，教授，博士生导师，研究方向为电磁兼容、电子设备故障诊断。

张 刚