基于参考磁链矢量计算的PMSM直接转矩控制

宁博文，刘莹，程善美，秦忆

(华中科技大学 自动化学院,湖北 武汉 430074)

基于参考磁链矢量计算的PMSM直接转矩控制

宁博文，刘莹，程善美，秦忆

(华中科技大学 自动化学院,湖北 武汉 430074)

为了减小传统直接转矩控制中较大的转矩和磁链波动，并使逆变器开关频率保持恒定，研究了一种基于参考磁链矢量计算的永磁同步电机直接转矩控制方法。从定子磁链矢量的变化所反映出的对转矩和磁链的控制作用考虑，对基于参考磁链矢量计算的直接转矩控制的原理和结构进行了详细地分析和论述。在此基础上，通过转矩方程局部线性化来获取转矩环的控制模型，在线性化过程中的误差进行分析的基础上，研究了转矩环PI控制器的参数设计方法。仿真和实验结果验证了所研究控制方法的可行性和有效性。

永磁同步电机；直接转矩控制；参考磁链矢量；空间矢量调制

0 引 言

永磁同步电机(permanent magnet synchronous motor,PMSM)具有转矩惯量比高、高效率以及高功率因数的优点，在中小功率电气传动领域有着广泛的应用[1-2]。直接转矩控制(direct torque control,DTC)是一种高性能的电机控制方法，在上个世纪80年代由日本学者Takahashi和德国学者Depenbrock分别提出，并首先在异步电机中得到应用。与矢量控制不同，直接转矩控制方法基于静止坐标系，不需要精确的位置反馈，且直接以转矩和磁链作为控制对象，具有快速的转矩响应性能，因此吸引了大量研究人员的关注。由于直接转矩控制的上述优点，随后被推广到永磁同步电机上，并成为了研究的热点[3-6]。

传统直接转矩控制结构简单，通过滞环控制器和开关表来选取输出的电压矢量；但由于在每一个控制周期中，只能从6个有效电压矢量中选取一个电压矢量来输出，因而存在转矩和磁链波动大、逆变器开关频率不固定以及电流谐波大等问题。围绕这些不足之处，众多学者对此进行了大量的研究工作[7-12]。

文献[7]提出了利用多电平变换器实现直接转矩控制的方案，可以有效地减小转矩和磁链波动；但由于电压矢量的可选择性增加，使得开关表变得复杂，且增加了硬件成本。文献[8]和文献[9]分别从对扇区进行了细分和在线调节滞环宽度考虑，来减小转矩和磁链波动；但是这些方法中，每一个控制周期仍然是只能输出一种电压矢量，因此改善效果有限。

应用空间矢量调制的直接转矩控制方法可以有效减小转矩和磁链波动，并使逆变器开关频率保持恒定。文献[13]从电机的非线性结构考虑，利用输入输出线性化控制理论，实现了对转矩和磁链的解耦控制；但是这种方法依赖于电机的参数。文献[14]提出了基于转矩和磁链滑模控制器的直接转矩控制，具有出色的转矩响应性能，且对参数的变化具有鲁棒性；但是存在抖振的问题。文献[15]应用两个PI控制器分别对转矩和磁链控制环节进行调节，来产生所需要的电压矢量；由于需要整定的参数较多，因而控制结构变得复杂。

为此，本文研究了一种基于参考磁链矢量计算的PMSM直接转矩控制方法，这种方法在转矩和磁链控制环中仅需要应用一个PI控制器，具有结构简单的优点。文中在详细分析其基本原理和结构的基础上，通过对转矩方程局部线性化，并结合转矩环控制变量间的关系，得到转矩环传递函数，进而对转矩环控制器参数进行设计。最后，仿真和实验验证了所提出方法的可行性和有效性。

1 基于参考磁链矢量计算的DTC基本原理

永磁同步电机的转矩方程可以表示为关于负载角的关系式，即

(1)

式中：np表示极对数；Ls表示定子绕组的电感；ψr和ψs分别表示永磁磁链和定子磁链；δ为负载角；kT=3npψrψs/2Ls为比例系数。由于电机的参数基本为恒值，因此当保持定子磁链幅值不变时，kT为常数。这样，转矩就只受到定子磁链和转子永磁磁链之间的夹角δ即负载角的控制。对式(1)求导，可以推出，一个控制周期中转矩变化和负载角变化之间的关系为

ΔTe=kTcosδΔδ。

(2)

由于控制周期很小，cosδ的值变化不大，因而转矩的变化与负载角的变化一致。在一个控制周期内，定子磁链矢量和转子永磁磁链矢量的变化示意图如图1所示，其中磁链矢量的幅值都保持不变。

图1 磁链矢量变化示意图Fig.1 Schematic diagram of flux vector variation circuit

图1中，定子磁链矢量角度的变化为Δθs，转子永磁磁链矢量角度的变化为ωTs，ω为电机转子的电角速度，Δδ为负载角的变化量，它们之间的关系为

Δθs=Δδ+ωTs。

(3)

(4)

因而对应于定子磁链矢量角度的变化，定子磁链矢量的变化量为：

(5)

描述了定子磁链矢量和电压矢量之间关系的定子磁链的电压方程为

(6)

由上式可知，定子磁链的变化实际上反映的是电压矢量对磁链矢量的控制作用，因而通过精确地控制电压矢量，可以补偿定子磁链矢量的变化。同样依据定子磁链的电压方程，可以求出对应于定子磁链矢量的变化，所需要的电压矢量为：

(7)

通过上述分析可知，电磁转矩所需要的改变，可以体现为定子磁链矢量角度的变化，另一方面对应于定子磁链矢量角度的变化所反映出的定子磁链的变化，最终可以通过电压矢量的控制补偿作用来实现。基于这一思想，可以采用PI控制器对转矩环进行控制，根据转矩的误差实时得到定子磁链矢量角度的增量，进而得到电机运行所需要的定子电压矢量，这种方法即为基于参考磁链矢量计算的直接转矩控制方法。其中，转矩环PI控制器的输入输出关系为

其次，在课程内容设计等方面加入职业相关的技能素养的培养，邀请校企双方专家一同评审“双证融通课程”的标准、教学方案和考核方案。依托专业群的支撑作用，设置了酒店管理概论、饭店服务标准、酒店服务礼仪等先导课程，为学生修读“双证融通课程”做好准备。从2013年始，先后与企业合作编写相关教材5部，这些被纳入江苏省十二五、十三五重点教材的最大特点就是将职业标准纳入到了教材体系。

(8)

式中：kp为比例系数；ki为积分系数。与传统控制方法一样，这种方法也是在静止坐标系上进行实现的，其控制结构框图如图2所示。从控制结构上看主要由4个部分组成，分别为参考磁链矢量计算模块、参考电压矢量计算模块、转矩和磁链观测模块，以及SVPWM调制模块。其中，转矩给定为速度控制器的输出，它与观测得到的反馈转矩之差，经过转矩环PI控制器调节输出得到定子磁链矢量角度的增量，再依据定子磁链矢量的给定幅值以及当前的定子磁链矢量的角度，计算得到定子磁链矢量的改变量，进而由磁链的电压方程计算得到参考定子电压矢量，最后结合空间电压矢量调制输出逆变器的驱动信号对电机进行控制。

图2 控制结构框图Fig.2 Block diagram of control structure

2 转矩环控制器参数设计

转矩环PI控制器中的参数对系统性能有着重要的影响，如果控制器PI参数设置不当，系统就可能得不到良好的转矩响应性能。本文通过对控制系统的模型进行分析，获取PI参数的设计方法。

在对转矩环PI控制器的参数进行设计时，首先需要抽象出控制系统的数学模型，在此基础上再进行参数的设计。依据上一部分的分析，可以得到转矩环的控制模型结构框图如图3所示。

图3 转矩环控制系统模型框图Fig.3 Model block diagram of torque loop control system

在转矩方程式中，转矩是关于负载角的正弦函数，即两者之间是非线性关系。为了简化控制器参数的设计过程，在研究系统、设计参数时尽可能考虑将非线性问题在合理的条件下简化为线性问题，再运用成熟的线性系统理论进行分析设计，故下面先对转矩方程的非线性部分进行近似的线性处理。

由于电机运行时，负载角δ的值非常小，可以认为

sinδ≈δ。

(9)

这样就对非线性函数sinδ进行了局部线性拟合。当负载角在(-30°，30°)范围时，线性拟合的曲线如图4所示。

从图4中可以看出，两条曲线基本重合。为了从量化角度对拟合的误差进行评估，定义拟合误差函数为

(10)

图4 线性拟合曲线Fig.4 Curve of linear fitting

由拟合误差函数表达式可以得到拟合误差函数曲线，如图5所示。可以看出，当负载角在(-30°，30°)范围时，拟合误差在5%范围之内。对于本文所应用的电机，其稳态运行时负载角在15°范围之内，因而拟合误差可以在3%之内，本文所应用电机的电气参数如表1所示。

图5 线性拟合误差曲线Fig.5 Curve of linear fitting error

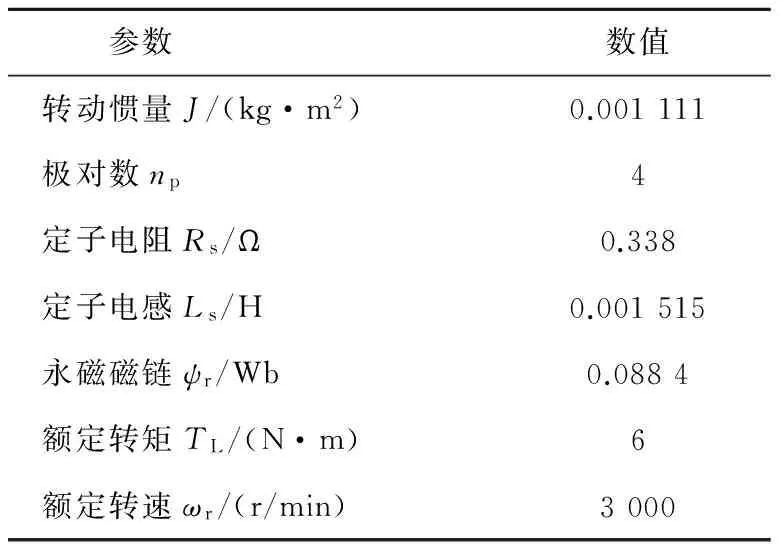
表1 PMSM主要参数Table 1 Main parameters of PMSM

经过线性拟合之后，转矩方程表示为

Te=kTδ。

(11)

这样就可以将图3所示的转矩环的控制环节抽象为控制对象和控制器两个部分，如图6所示。

图6 转矩环系统抽象模型Fig.6 Abstract model of torque loop system

转矩环控制对象的传递函数为

(12)

而抽象出的控制器的传递函数为

(13)

其中Ts为采样周期。根据简化的转矩环控制框图图6，可以求得转矩环的传递函数为

(14)

所得到的转矩环传递函数是一个二阶系统，通常二阶系统的特征方程为

(15)

其中：ωn为自然角频率；ζ为阻尼系数。将转矩环传递函数的特征方程与二阶系统的特征方程相对应，可以得到：

(16)

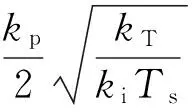
(17)

由此，可以求得相应的控制器参数为：

(18)

(19)

当采样周期Ts确定时，由阻尼系数ζ和自然角频率ωn就可以得到控制器的参数。

在求取控制器参数的过程中，先忽略了扰动对系统的影响。在扰动作用下，系统的稳态响应误差为

(20)

由于转矩环控制周期较快，速度的变化相对于转矩的控制而言是很慢的，因而扰动信号ω在每一个转矩环控制周期中可以看成是恒定的，那么ω(s)=ω/s，这样利用拉氏变换的终值定理，可以求取扰动信号作用时系统的稳态误差为

0。

(21)

因此外部扰动并不会对系统的稳态运行造成影响。

3 仿真与试验研究

依据上述分析和图2所示的基于参考磁链矢量计算的PMSM直接转矩控制的结构框图，在Matlab中搭建了仿真模型进行仿真研究，并在以TMS320F28335为核心控制器搭建的控制平台上进行了实验研究。在仿真和实验中，速度环控制周期为1 kHz，转矩环控制周期10 kHz，转矩波动Tripple和定子磁链的波动ψripple的计算式为：

(22)

图7所示为取不同的PI参数时，由图3所得到的转矩环控制模型和实际系统的转矩阶跃响应波形。其中自然角频率ωn取值为1 000 rad/s，在图7(a)中阻尼系数ζ=1，因此转矩控制器的PI参数值为kp=0.006 462，ki=3.231。而在图7(b)中，阻尼系数ζ=2，对应的转矩控制器的PI参数值为kp=0.012 9，ki=3.231。可以看出，实际系统的转矩响应与转矩环模型的响应基本相同，这说明上述提出的系统局部近似线性化后建模的正确性。

图8为基于参考磁链矢量计算的PMSM直接转矩控制的转速响应、转矩响应以及定子磁链响应的仿真波形。仿真中的速度给定为1 500 r/min，负载转矩在0.5 s时从空载变为额定负载6 N·m，定子磁链给定值为0.884 Wb。基于参考磁链矢量计算方法中的转矩环PI控制器中kp=0.012 9，ki=3.231。可以看出，在运行过程中的不同状态下，定子磁链幅值可以保持恒定。

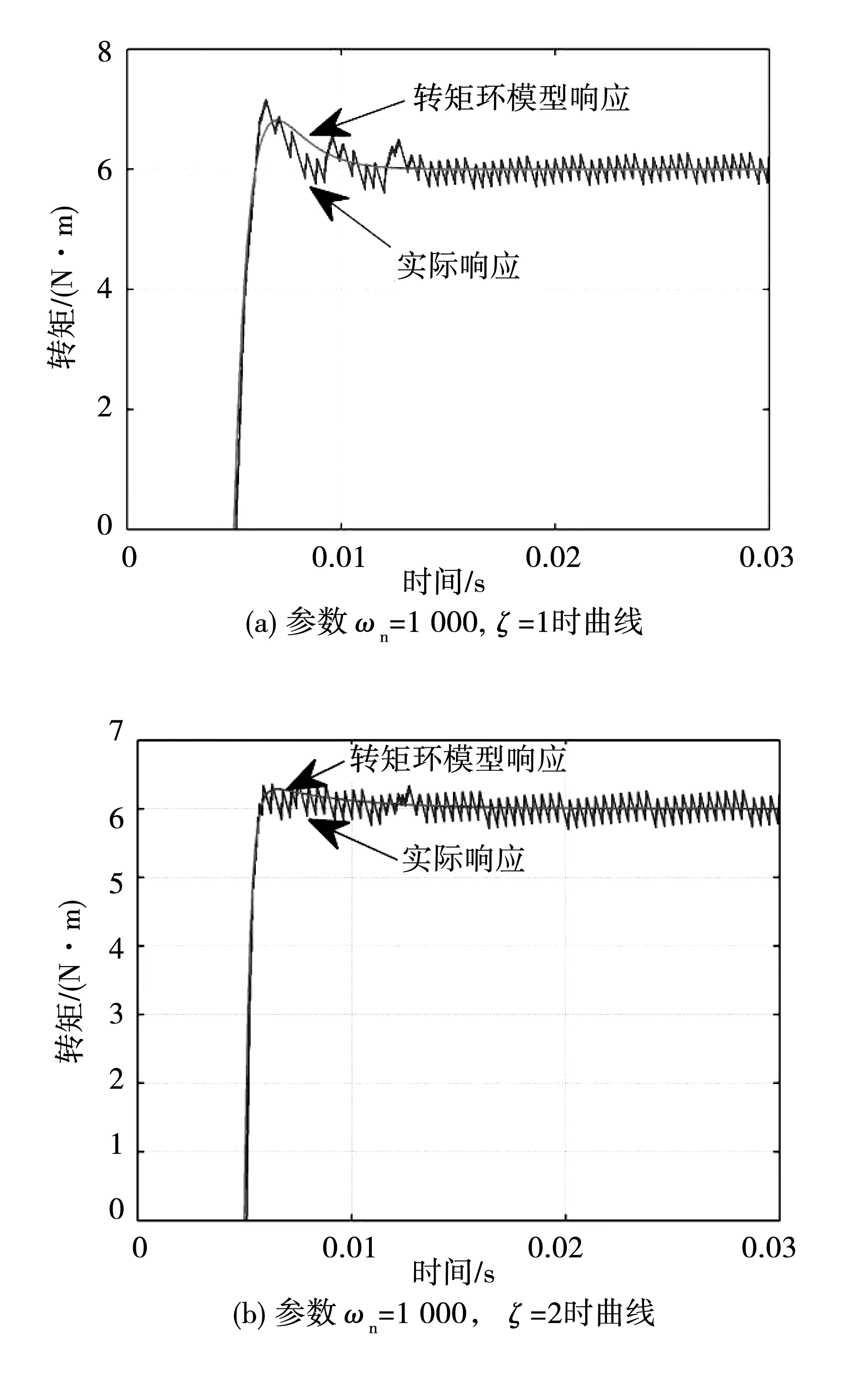
图7 转矩环响应曲线Fig.7 Response curve of torque loop

传统DTC方法和基于参考磁链矢量计算DTC方法的实验波形如图9和图10所示，其中转速给定为斜坡给定。从转速实验波形可以看出，由于采用斜坡给定的启动方式，实际转速不会出现较大的超调量，在1 000 r/min情况下到达给定转速的时间为0.1 s。从实验结果可以看出，传统DTC方法的缺点是转矩和定子磁链的波动都较大，依据式(22)，可得1 000 r/min稳态运行时转矩波动和磁链波动分别为Tripple=2.078 9 N·m和ψripple=0.004 7 Wb。

在参考磁链矢量计算DTC控制方法中，转矩环PI参数按照文中所论述的方法进行取值，在1 000 r/min空载运行时的实验波形如图10所示。可知在1 000 r/min运行时，其转速响应快速，调节时间为0.1 s，与传统DTC方法相同。从转矩响应实验波形可以看出，转矩反馈能快速地跟上转矩给定，反映了转矩快速的响应性能。从定子磁链响应实验波形可以看出，此时磁链幅值保持恒定，基本与给定值相等。由于采用空间电压矢量调制的方式输出，转矩和定子磁链受更多电压矢量的控制，它们的波动明显地减小。依据式(22)，在1 000 r/min运行时，转矩波动为Tripple=0.092 6 N·m，磁链波动为ψripple=0.000 314 31 Wb，相比于传统DTC方法，波动显著减小。

图8 基于参考磁链矢量计算的DTC仿真波形Fig.8 Simulation waveforms of DTC based on reference flux vector calculation

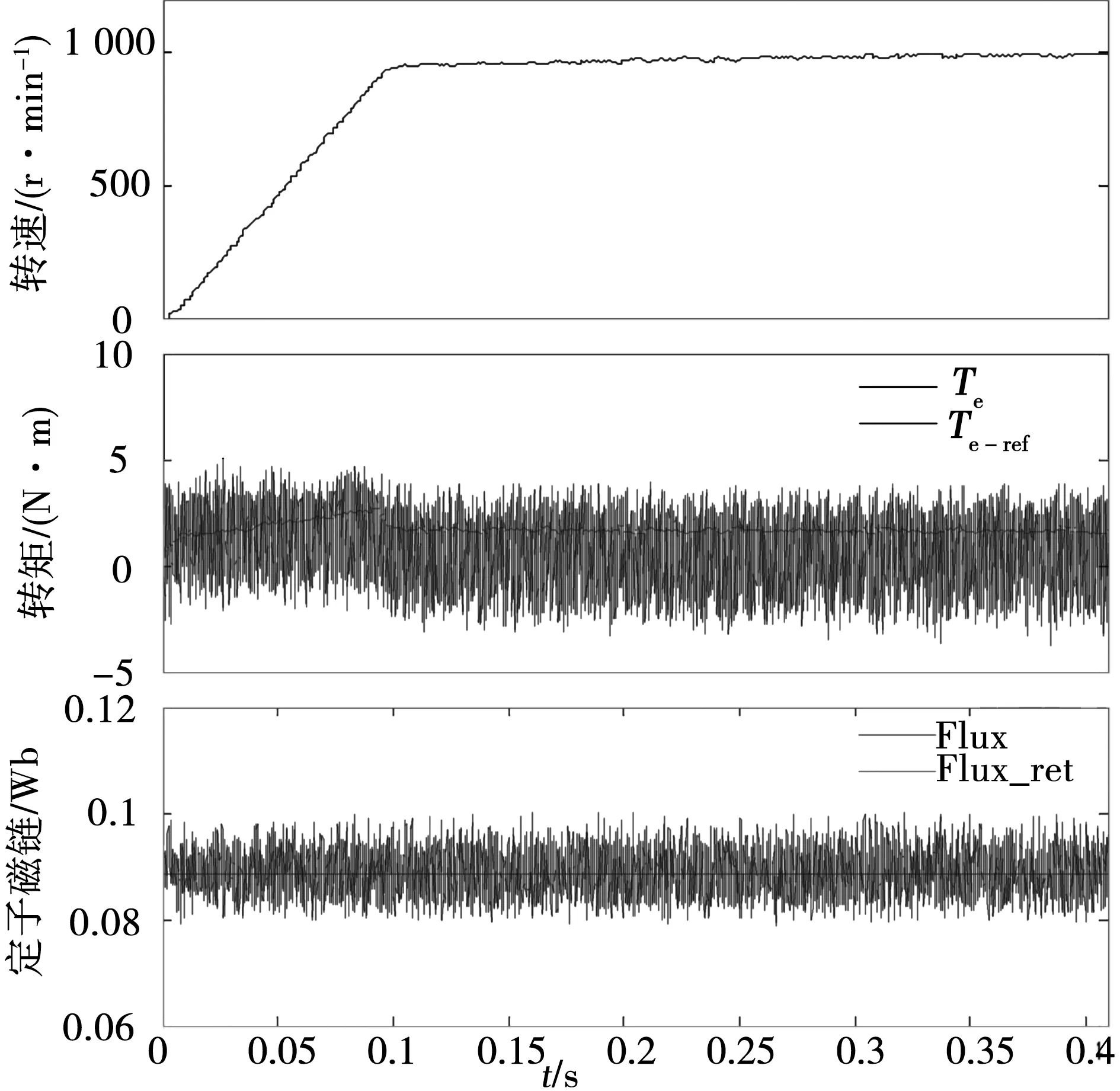
图9 传统DTC实验波形Fig.9 Experimental waveforms of the conventional DTC

图10 基于参考磁链矢量计算DTC实验波形Fig.10 Experimental waveforms of DTC based on reference flux vector calculation

4 结 论

为了在改善转矩和磁链波动的同时，使逆变器的开关频率保持恒定，研究了基于参考磁链矢量计算的PMSM直接转矩控制方法。文中分析了定子磁链矢量的变化和转矩的关系，由定子磁链矢量的增量求取所需要的电压矢量，以补偿定子磁链和转矩的误差，并通过空间矢量调制方式对电压矢量输出。在此基础上，通过对转矩方程局部线性化来获取转矩环的控制模型，并对转矩环PI控制器的参数进行了设计。仿真和实验结果表明，所研究的方案可以有效减小转矩和磁链波动。

[1] ZHU H,XIAO X,LI Y.Torque ripple reduction of the torque predictive control scheme for permanent magnet synchronous motors[J].IEEE Transactions on Industrial Electronics,2012,59(2):871.

[2] 唐任远.现代永磁同步电机理论与设计[M].北京:机械工业出版社,1997:96-135.

[3] ZHONG L,RAHMAN M F,HU W Y,et al.Analysis of direct torque control in permanent magnet synchronous motor drives[J].IEEE Transactions on Power Electronics,1997,12(3):528.

[4] BUJA G S,KAZMIERKOWSKI M P.Direct torque control of PWM inverter-fed AC motors—a survey[J].IEEE Transactions on Industrial Electronics,2004,51(4):744.

[5] NIU F,WANG B,BABEL A S,et al.Comparative evaluation of direct torque control strategies for permanent magnet synchronous machines[J].IEEE Transactions on Power Electronics,2016,31(2):1408.

[6] 杨影,陈鑫,涂小卫,等.占空比调制的永磁同步电机直接转矩控制[J].电机与控制学报,2014(4):66.YANG Ying,CHEN Xin,TU Xiaowei,et al.Direct torque control of permanent magnet synchronous motor based on duty ratio control[J].Electric Machines and Control,2014(4):66.

[7] 林磊,邹云屏,王展,等.一种具有中点平衡功能的三电平异步电机直接转矩控制方法[J].中国电机工程学报,2007,27(3):46.LIN Lei,ZOU Yunping,WANG Zhan,et al.A DTC algorithm of induction motors fed by three-level inverter with neutral-point balancing control[J].Proceedings of the CSEE,2007,27(3):46.

[8] 廖晓钟,邵立伟.直接转矩控制的十二区段控制方法[J].中国电机工程学报,2006,26(6):167.LIAO Xiaozhong,SHAO Liwei.The twelve-section control methods of direct torque control[J].Proceedings of the CSEE,2006,26(6):167.

[9] UDDIN M,HAFEEZ M.FLC-based DTC scheme to improve the dynamic performance of an IM drive[J].IEEE Transactions on Industry Applications,2012,48(2):823.

[10] 徐艳平,钟彦儒.基于占空比控制的永磁同步电机新型直接转矩控制策略[J].电工技术学报,2009,24(10):27.XU Yanping,ZHONG Yanru.A novel direct torque control strategy of permanent magnet synchronous motors based on duty ratio control[J].Transactions of China Electrotechnical Society,2009,24(10):27.

[11] ZHANG Y,ZHU J.Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J].IEEE Transactions on Power Electronics,2011,26(1):235.

[12] 李政学,张永昌,李正熙,等.异步电机新型占空比直接转矩控制方案[J].电工技术学报,2015,30(24):23.LI Zhengxue,ZHANG Yongchang,LI Zhengxi,et al.A novel direct torque control strategy of induction machine drives with simple duty ratio calculation[J].Transactions of China Electrotechnical Society,2015,30(24):23.

[13] 周扬忠,许海军,毛洁.永磁同步发电系统中转矩和磁链精确线性化解耦控制[J].中国电机工程学报,2012,32(24):96.ZHOU Yangzhong,XU Haijun,MAO Jie.Precision linearization decoupling control for torque and flux linkage of permanent synchronous generating system[J].Proceedings of the CSEE,2012,32(24):96.

[14] XU Z,RAHMAN M F.Direct torque and flux regulation of an IPM synchronous motor drive using variable structure control approach[J].IEEE Transactions on Power Electronics,2007,22(6):2487.

[15] 张华强,王新生,魏鹏飞,等.基于空间矢量调制的直接转矩控制算法研究[J].电机与控制学报,2012,16(6):13.ZHANG Huaqiang,WANG Xinsheng,WEI Pengfei,et al.Study on direct torque control algorithm based on space vector modulation[J].Electric Machines and Control,2012,16(6):13.

(编辑：刘琳琳)

DirecttorquecontrolofPMSMbasedonreferencefluxvectorcalculation

NING Bo-wen，LIU Ying，CHENG Shan-mei，QIN Yi

(School of Automation,Huazhong University of Science and Technology,Wuhan 430074,China)

In order to reduce the larger torque and flux ripples of the traditional direct torque control,and obtain the constant inverter switching frequency,an improved direct torque control method of PMSM based on reference flux vector calculation was studied.The principle and structure of the direct torque control with reference flux vector calculation was discussed in-depth by analyzing the control effect of the change of the stator flux vector on the torque and flux.Then the torque loop control model was obtained by partly linearizing the torque equation,and the parameter of the torque loop controller was designed after analyzing the error of the linearization procedure.Finally,the feasibility and validity of the studied control method was verified by the simulation and experiment results.

permanent magnet synchronous motors; direct torque control; reference flux vectors; space vector modulation

10.15938/j.emc.2017.09.001

TM 351

:A

:1007-449X(2017)09-0001-07

2016-08-22

宁博文(1987—)，男，博士研究生，研究方向为电力电子和电气传动；刘 莹(1988—)，男，博士研究生，研究方向为电力电子和电气传动；程善美(1966—)，男，博士，教授，研究方向为电力电子和电气传动，智能控制技术；秦 忆(1945—)，男，教授，博士生导师，研究方向为电力电子和电气传动。

宁博文