岸边溢洪道进水口导流墙压强特性的数值模拟研究

武华宝

（山东农业工程学院国土资源与测绘工程学院，山东济南250100）

岸边溢洪道进水口导流墙压强特性的数值模拟研究

武华宝

（山东农业工程学院国土资源与测绘工程学院，山东济南250100）

文章以某大型水库岸边溢洪道进水口为研究对象，针对物理模型试验中溢洪道进水口处左岸回流、右岸出现漩涡的问题，应用Realizable k-ε湍流模型、VOF法模型追踪自由表面和非结构网格区域离散进行处理，对水库溢洪道进水口进行三维数值模拟计算，并结合1:80的物理模型试验成果对比分析，结果表明VOF模型能较好的反映出溢洪道进水口的压力场分布，与模型试验的结果吻合较好。其数值计算结果可以为岸边溢洪道进水口压强分布规律提供较为可靠的依据，研究成果也为其他类似的水工建筑物的进水口问题提供了参考。

溢洪道进水口；Realizable k-ε；漩涡；压强特性

引言

岸边式溢洪道由于受到占地面积的限制，建筑物尺寸不足，因而溢洪道进水口处难以平顺的扩散到导流墙，使得闸室前的进水口区域出现回流、漩涡或出现负压等不良的水流现象，严重时甚至会导致导流墙失稳，另外，水流产生的负压还与空化汽蚀等问题有关。因而对溢洪道进水口处压力特性进行深入研究具有重要的意义。近年来，随着计算机技术的发展和应用，以VOF处理自由表面、k-ε模型为基础的数值模拟技术已成为研究复杂水流特性的有效工具[1]-[4]。本文以某一大型水库岸边溢洪道为例，采用VOF法追踪自由水面、基于Realizable k-ε湍流模型对溢洪道进水口的进行三维数值模拟，并与试验数据进行对比分析，得到复杂边界条件下溢洪道进水口导流墙段的压力特性分布，为泄水建筑物的水力设计提供依据[5][6]。

1．数学模型和计算方法

1.1 控制方程

溢洪道进水口边界较为复杂，在大流量泄水时，进水口右岸出现漩涡、负压和左岸出现回流，而Realizable k-ε模型可以更好的处理脱流、复杂的二次流动以及带有分流的流动[7]。为了更好的处理溢洪道进水口复杂的自由液面，本文采用Realizable k-ε模型和VOF法来模拟溢洪道进水口的水流。

（1）Realizable k-ε模型的k方程和ε方程为：

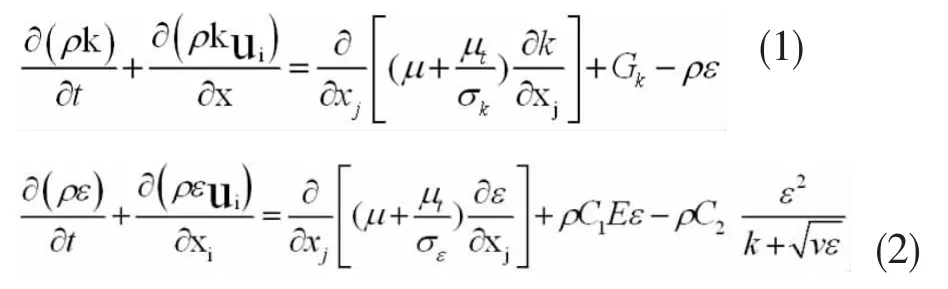
公式中：

ui为 x、y、z三个方向上的速度分量 (i=1,2,3)；бk=1.0，бε=1.2，C2=1.9。

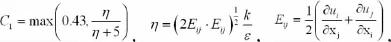
1.2 VOF法处理自由液面

VOF法是处理复杂的自由液面简单有效的方法，该方法比较适合两种或两种以上互不穿透的流体界面计算[7]-[10]。假设自由表面在同一单元中，水和气体容积比满足连续方程，水和气的容积比之和为1，而整个流场中对应的体积分数α为变量，该公式应满足：

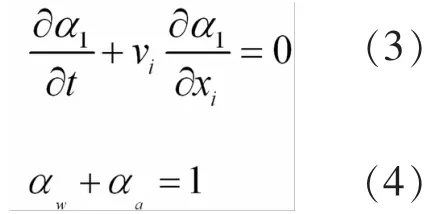
在每个计算单元体内，若αw=0，表示单元体内全为气体；当0＜αw＜1时，表示单元体内包含液体和气体，当αw=1时，表示单元体内全部是液体。

1.3 工程实例

济南市卧虎山水库是以防洪为主，兼顾城市供水、农业灌溉等功能的大型水库，溢洪道位于坝体最左岸，溢洪道全长242.12m，主要有进口段、控制段、泄槽段和出水渠组成，其中闸前进口段长33.50m，控制段为5孔闸室，闸室长28m，每孔宽14m，总净宽70m，闸底板高程118.3m，门槽处驼峰堰的堰顶高程121.0m，弧形钢闸门的尺寸为14×11m，泄槽段129.5m，宽78m，库区进水段的布置如图 1、2 所示。

图1 溢洪道进水口布置图

图2 溢洪道模型试验布置图

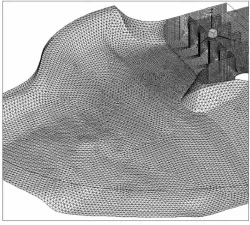
图3 网格划分图

图4 裹头处传感器测点布置图

本文采用FLUENT软件，根据库区的进水口段工程实例按1:1的比例建立三维湍流数学模型，由于库区及溢洪道进水口的边界条件较为复杂，闸室控制段比较规则，因此在库区和进水口段采用疏密程度不同的非结构网格、闸室控制段采用均匀的网格划分计算区域，网格总数为227462个。溢洪道计算区域和效果如图3。

2．溢洪道进水口段脉动压力的实验方案

前期的模型试验研究表明，溢洪道进水口段在流量到达校核洪水的流量(Q=7030m3/s)时，进水口区的右岸裹头处 （断面0-12.5m和0-53.5m之间）有紊流较为严重并伴有漩涡产生，因此在右岸裹头横向沿水流取4个断面，高程在124.5m，127.7m和130.9m处安装12个脉动压力传感器，脉动压力传感器用DJ800多功能采集系统进行同步采集，采样时间为10s，采样间隔为0.01s，每个样本容量N=10000。并采用随机函数理论的数据统计分析方法，对试验数据进行处理和频谱分析。压力传感器布置如图5。

物理模型试验的整体布置图见图2，模型试验的各水力参数设置，试验条件对应的流量、库水位如表1、2所示。

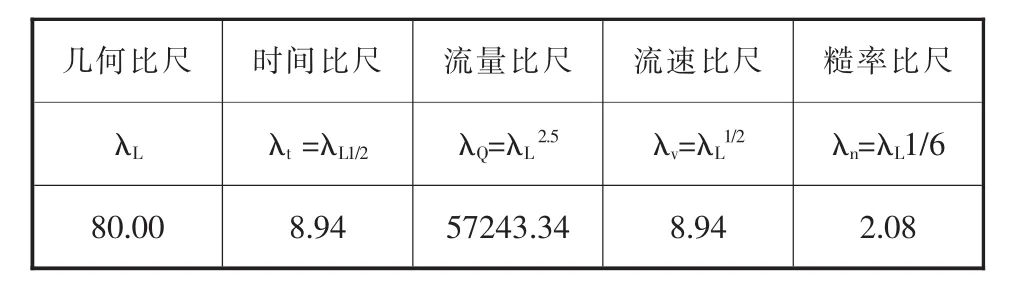
表1 试验模型的各个比尺参数设置

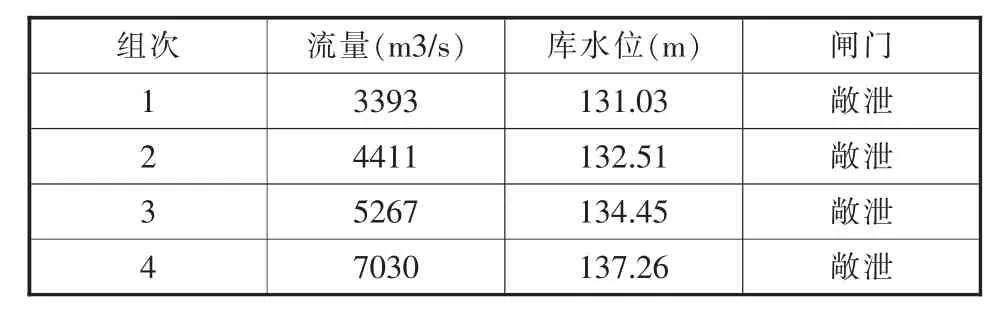
表2 实验条件及方案

3.试验与数值模拟对比分析

3.1 时均压力分析

在大流量工况下（Q＞3393 m3/s），试验测得和数值模拟计算均表明，进水口的左岸水面出现回流，当水位到校核洪水位137.26m，流量为7030 m3/s时，试验和数值模拟均显示出右岸裹头处水流紊乱严重，且在断面0-12.5m和0-53.5m之间出现了较大范围的漩涡。从时均压力沿水深的分布看（图10），对于各断面在124.5m，127.7m和130.9m三个高程上的压力分布基本上是一直线，这与静水压力的分布规律相似，断面3处因为漩涡中心，其沿水深变化率较大。在沿水流方向上，裹头处的沿程时均压强的规律是断面1最大，然后减小再增大的趋势，时均压强的最大值为13.89m，出现在裹头的测点3处，这是由于断面1处与水流的流向垂直，水流的动能转换为压能，而最小值出现在断面3的测点7处，在该断面上，水流流速增大，离心力占主导作用，同时伴随漩涡，有负压产生为-3.97m，而在断面4处，裹头处断面收缩，漩涡消失，水流开始稳定，动水压强开始增大，这一变化规律与水流现象是一致的。该工况条件下数值模拟计算压强图和沿水流方向的时均压力图如图5-10。

图5 数值模拟计算压强图

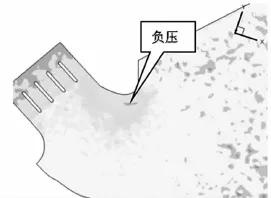
图6 高程130.9m截面压强图

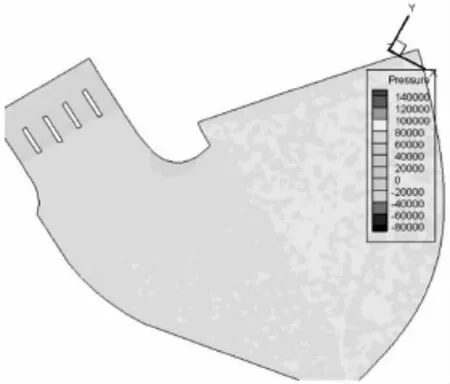
图7 高程127.7m截面压强图

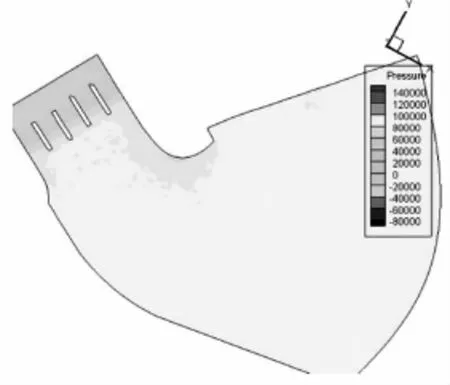
图8 高程124.5m截面压强图

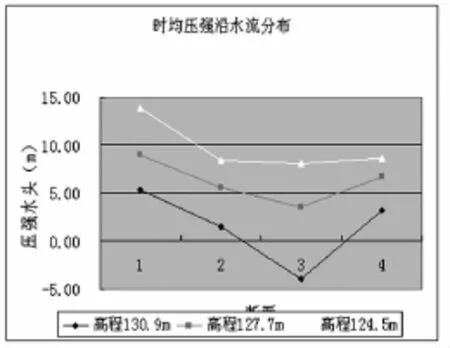
图9 时均压强沿程分布

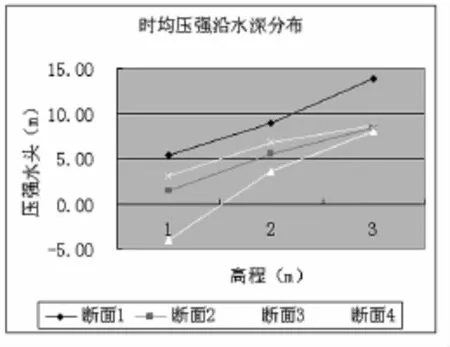
图10 时均压力沿水深的分布

3.2 脉动压力分析

水流脉动压力不仅会导致水流瞬时空化数减小，严重时会产生空蚀，而且脉动压力也是水工建筑物结构产生振动的重要随机荷载。以下在幅域和频域两方面进行分析。

3.2.1幅域分析

脉动强度一般由脉动压强的均方根直接反映。其公式为：

式中：为时均压强，为标准差。

现取在校核洪水位流量（7030 m3/s）来分析，裹头上的脉动压力均方根值如表3，脉动压力沿水深、水流方向的分布如图11、12，各级流量的脉动压强如表4。

从表3、4和图11、12可以看出，在各级流量条件下，脉动压力最大的位置同样在漩涡出现的位置7号测点处，其他测点脉动压力较小，这说明紊流强度与脉动压力密切相关，脉动压力随着紊流强度的增大而增大。而在靠近底部的测点脉动压力较小，受紊流的冲击比较小，同时，在高程上看，较高测点的位置，脉动压力较大，这也是因为上部位置受紊流影响较大所致。

表3 裹头上脉动压力均方根值（Q=7030 m3/s）

表4 各流量下脉动压力均方根值

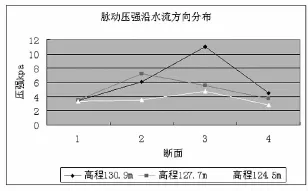
图11 脉动压力沿水流方向分布

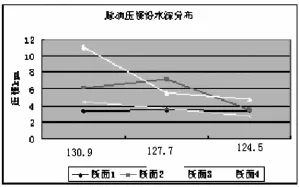
图12 脉动压力沿水深分布（Q=7030 m3/s）

3.2.2频域分析

从图13可以看出，裹头上的脉动压力优势频率在漩涡处脉动频率较高，其他处频率较低，且随着流量的增大而增加，这与水流流态、流速大小及流速的均匀度都是密切相关的，但仍属于低频脉动 （在0.002～0.026Hz之间），因而不会引起破坏性的震动。

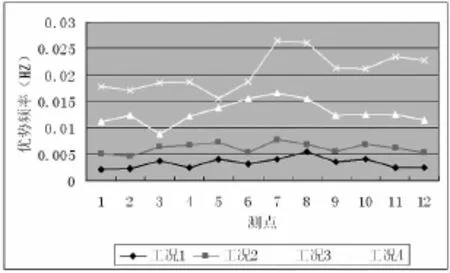
图13 各级流量下脉动压力优势频率图

3.2.3空化气蚀分析

在水力学计算中，一般用水流空化数(б)作为水流空化气蚀的判别参数，计算公式为：

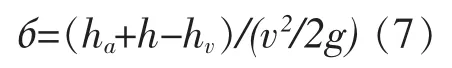
考虑到最大脉动压力的影响，计算水流的瞬时空化数公式为：

式中：ha按（10.33-／900）计算，为断面处大气压力 （m），h 为断面处时均动水压力（m），P＇max为最大脉动压力值，hv为水的汽化压力水柱高度。

根据以上公式，计算断面3上测点7处的水流的空化数最小为2.32，瞬时水流空化数为1.89，该数值远远大于初生空化数 бi（бi＜0.6）,因此不会产生空蚀。

4．结论

（1）借助FLUENT软件，Realizablek-ε湍流模型、VOF法模型追踪自由表面和非结构网格区域离散进行处理，对水库溢洪道进水口进行三维数值模拟计算，重点分析了进水口裹头处的压力场分布规律，在与物理模型试验数据对比分析验证，结果表明数值模拟计算结果与模型试验结果吻合度较好，数值计算结果可以为岸边溢洪道进水口压强分布规律提供较为可靠的依据。

（2）脉动压力与水流流态密切相关，无论是时均压力还是脉动压力，均受到紊流和漩涡的影响。校核洪水位条件下，时均压力在裹头的断面3测点7处出现最小值，且产生负压，其沿水流的变化规律是从大到小再到大的规律分布。而脉动压力也是由于在断面3处水流流态最差且出现漩涡等不良水力条件，因此该处也是脉动压力最大值的出现点。而在紊流并未直接冲击到的水流底部时，脉动压力和幅值变化均比较小，这表明水流紊动强度越大、表面漩滚越大，其脉动压力也随之增大。

（3）岸边式溢洪道进水口裹头在大流量条件下流态较为紊乱，且容易在转弯处出现脱流甚至出现漩涡，该位置也是脉动频率最高值的所在，但该频率属于低频脉动，空化数和瞬时水流空化数远远大于初生空化数，因此不会引起建筑物的破坏或震动。

[1]陈群、戴光清.鱼背山水库岸边阶梯溢洪道流场的三维数值模拟[J].水力发电学报，2002（3）：62-72．

[2]任双立、吕勋博.Fluent软件在溢洪道泄流中的应用[J].电网与清洁能源，2014（7）:77-80.

[3]郭红民、向光明、谢洋、李江、毛家河水电站溢洪道三维数值模拟.[J].水电能源科学，2013（3）：81-85.

[4]王青，黄细彬.基于Flow－3D的陡坡弯道水流三维数值模拟[J]水资源与水工程学报，2016（10）：145-149.

[5]李玲、陈永灿、李永红、三维VOF模型及其在溢洪道水流计算中的应用[J].水力发电学报，2007，26（4）： 83-87.

[6]沙海飞、周辉、吴时墙等.多孔溢洪道泄流三维数值模拟[J].水利水电技术，2005，36（10）：42-46.

[7]王福军．计算流体动力学分析[M]．北京：清华大学出版社，2004．

[8]江 帆、黄鹏、Fluent高级应用于实例分析[M].北京:清华大学出版社，2008．

[9]张 健、方 杰、范波芹、VOF方法理论与应用综述[J]．水利水电科技进展，2005，25(2):67-90.

[10]李冰冻、李嘉、李克锋等．VOF方法在山区河流航道工程中的应用[J]．中国水运，2009，9(2):26-28．

编辑：董刚

A Numerical Study on the Pressure Properties of the Diversion Wall at the Inlet of a Bank-run Spillway

WU Huabao
（Department of Territory Information and Mapping Engineering,Shandong Agricultural and Engineering University，Jinan Shandong 250100）

This article studies on the pressure properties of the diversion wall at the inlet of the spillway on the banks of a large reservoir.A three-dimensional numerical model is developed to analyze the occurrences of a left-bank backflow and a right-bank vortex observed by a physical model.The Realizable k-ε turbulence model and the VOF model are used respectively to simulate the trajectory of the free surface and to discretize the unstructured grids.The results are compared with that of the physical model test on the scale of 1:80.It is revealed that the VOF model can reasonably represent the pressure distribution at the inlet of the spillway,and the modelling results coincide with the physical model test.The numerical simulation results in this study provide a useful reference for similar studies on the pressure distribution at the inlet of a spillway as well as the inlets of other hydraulic structures.

spillway inlet；Realizable k-ε turbulence model；vortex；pressure property

TV32

A

2095-7327（2017）-09-0039-05

武华宝（1983-），男，山东泰安人，山东农业工程学院讲师，硕士，研究方向：水工结构工程和工程项目管理。