基于Cauchy分布模型与NSST变换的图像去噪算法

王相海, 朱毅欢, 耿 丹, 宋传鸣

(1.辽宁师范大学 计算机与信息技术学院, 辽宁 大连 116029; 2.辽宁师范大学 数学学院, 辽宁 大连 116029)

基于Cauchy分布模型与NSST变换的图像去噪算法

王相海1, 朱毅欢1, 耿 丹2, 宋传鸣1

(1.辽宁师范大学 计算机与信息技术学院, 辽宁 大连 116029; 2.辽宁师范大学 数学学院, 辽宁 大连 116029)

非下采样Shearlet变换(NSST)具有良好的方向敏感性，各向异性以及平移不变性，是接近最优的多尺度稀疏表示方法.提出一种基于先验柯西(Cauchy)模型的NSST域图像去噪方法, 利用Cauchy分布对NSST变换域子带系数概率分布进行拟合，作为先验分布模型，再通过最大后验概率(MAP)方法估计不含噪声的系数.该方法不但保留了传统统计模型去噪方法中的优点，还通过对NSST具有更好拟合效果的柯西分布模型作为先验的概率分布模型，使估计出的系数更接近于原始图像的系数.大量仿真实验验证了所提出方法的有效性.

非下采样Shearlet；Cauchy分布模型；最大后验概率；图像去噪

图像在采集和传输过程中不可避免地会受到噪声的污染，因此图像去噪作为图像处理的重要研究领域一直受到高度重视，同时它通常也是更深层次图像处理的基础性工作.图像去噪的目标是在有效去除图像噪声的同时，尽可能地保留图像边缘、纹理等细节信息.近年来，基于小波变换多尺度特性和局部特性的图像去噪方法受到关注，然而虽然小波变换可以很好地捕捉一维信号的奇异性，但是对二维信号的轮廓、边缘和纹理等高维奇异特性的捕捉效果并不理想，为了更好地表示图像的这种高维奇异特性，Ridgelet、Curvelet、Contourlet等多尺度几何工具被提出[1]，特别是近年来被提出的Shearlet变换[2]作为小波变换在多维方向的自然扩展，其基函数具有可变的楔形支撑空间，能够通过剪切和膨胀自适应表示图像的几何边缘，接近最优的二维图像的稀疏表示[3-8].

在基于多尺度变换的图像去噪方法中阈值去噪方法通常以简单著称，它将图像的变换域系数当作确定的独立信号进行处理.虽然多尺度变换具有解相关性，但图像多尺度变换子带之间还是会存在一定的联系，如何有效地确定这些系数之间的关系，并使之对图像多尺度变换系数进行有效评估成为基于统计模型图像去噪方法的一个关键问题.事实上，基于多尺度变换的统计模型去噪方法通常需要解决两个问题[9]，一是系数子带的先验概率模型选取问题；另一个是去噪方法的确定.常用的多尺度子带系数的概率分布模型有广义高斯分布(GGD)[10]和拉普拉斯分布(Laplacian)[11]等.本文通过大量实验统计表明，Cauchy分布能够更好地对Shearlet域子带系数进行拟合.基于此，将Cauchy分布模型作为先验概率模型，并采用最大后验概率对Shearlet子带系数进行估计，在此基础上实现去噪操作，取得了很好地去噪效果.

1 NSST变换概述

K.H.Guo和D.Labate提出的Shearlet变换具有完备的构造理论框架和严格的数学逻辑支持，是仿射系统对多维信号几何特征提取的一个最有效的方法[2,8].该变换作为一种新型的多尺度变换继承了Contourlet变换与Curvelet变换的优点，其与Curvelet变换具有相同的图像近似阶数，但实现更加简单，同时尺度方向比Contourlet变换更加灵活.对于二维信号，Shearlet变换不仅能够检测其所有的奇异点，同时还能够自适应的追踪奇异曲线的方向.

Shearlet变换由合成小波理论衍生而来，当维n=2时，具有合成膨胀的仿射系统定义为

ΨAB(ψ)={ψj,k,l(X)=|detA|j/2ψ(BlAjX-k):j,l∈,k∈2}.

其中，ψ∈L2(2)，A和B为2×2的可逆矩阵，detΒ=1.

如果ΨAB(ψ)满足Parseval框架，即对任意f∈L2(2)有

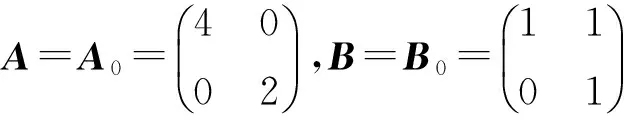
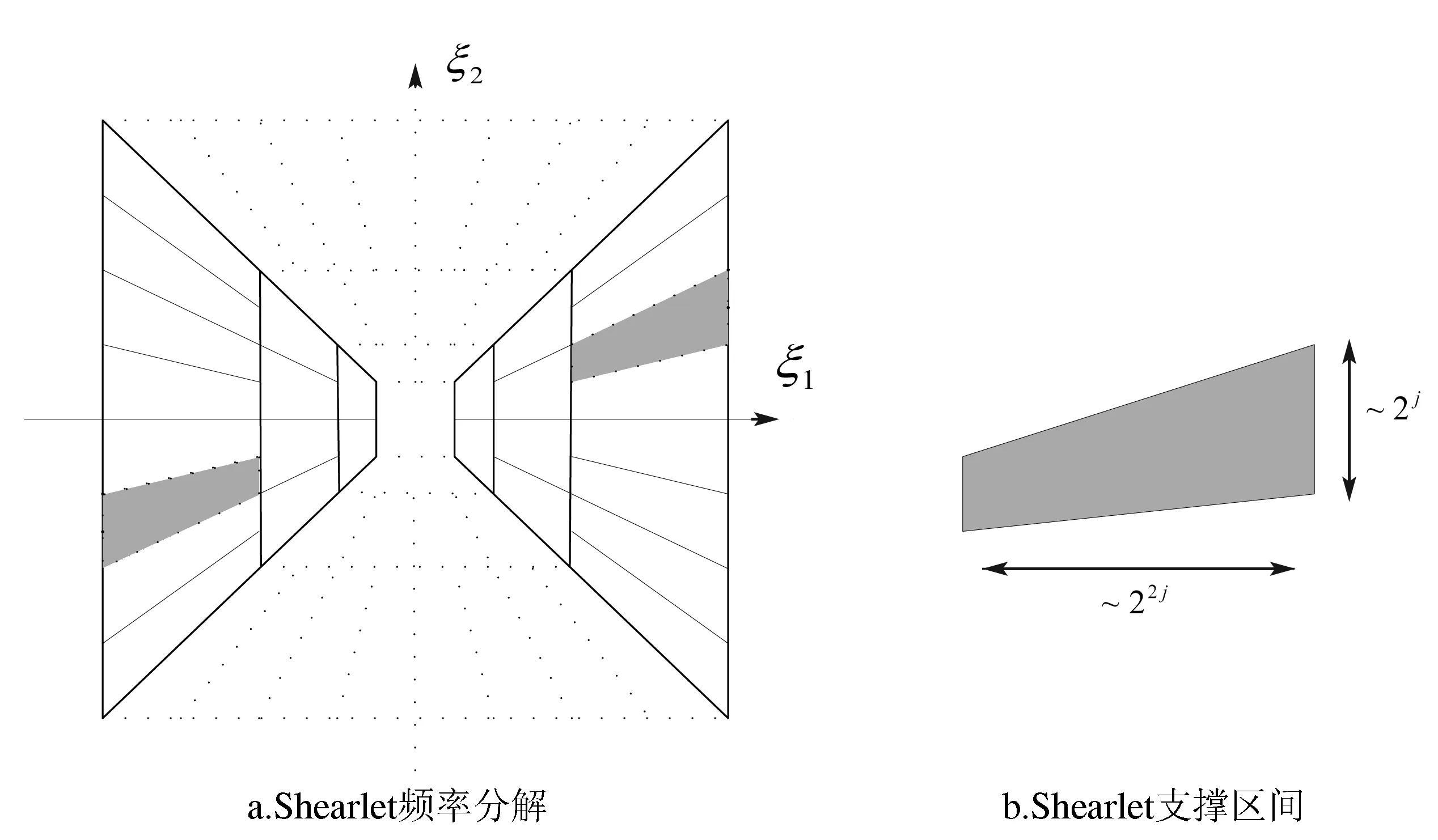
图1 Shearlet变换频率分解和支撑区间Fig.1 Frequency decompositions by the shearlet transform and frequency support of a shearlet

为了使Shearlet变换具有平移不变特性，仿造非下采样轮廓波变换(Nonsubsampled Contourlet Transform，NSCT)的构造方法，文献[13]中通过用非下采样的Laplacian金字塔算法替换Laplacian金字塔算法，构造了非下采样剪切波变换(Nonsubsampled Shearlet Transform，NSST).NSST分解过程如图2所示，图像经过两层NSST分解实例如图3所示.

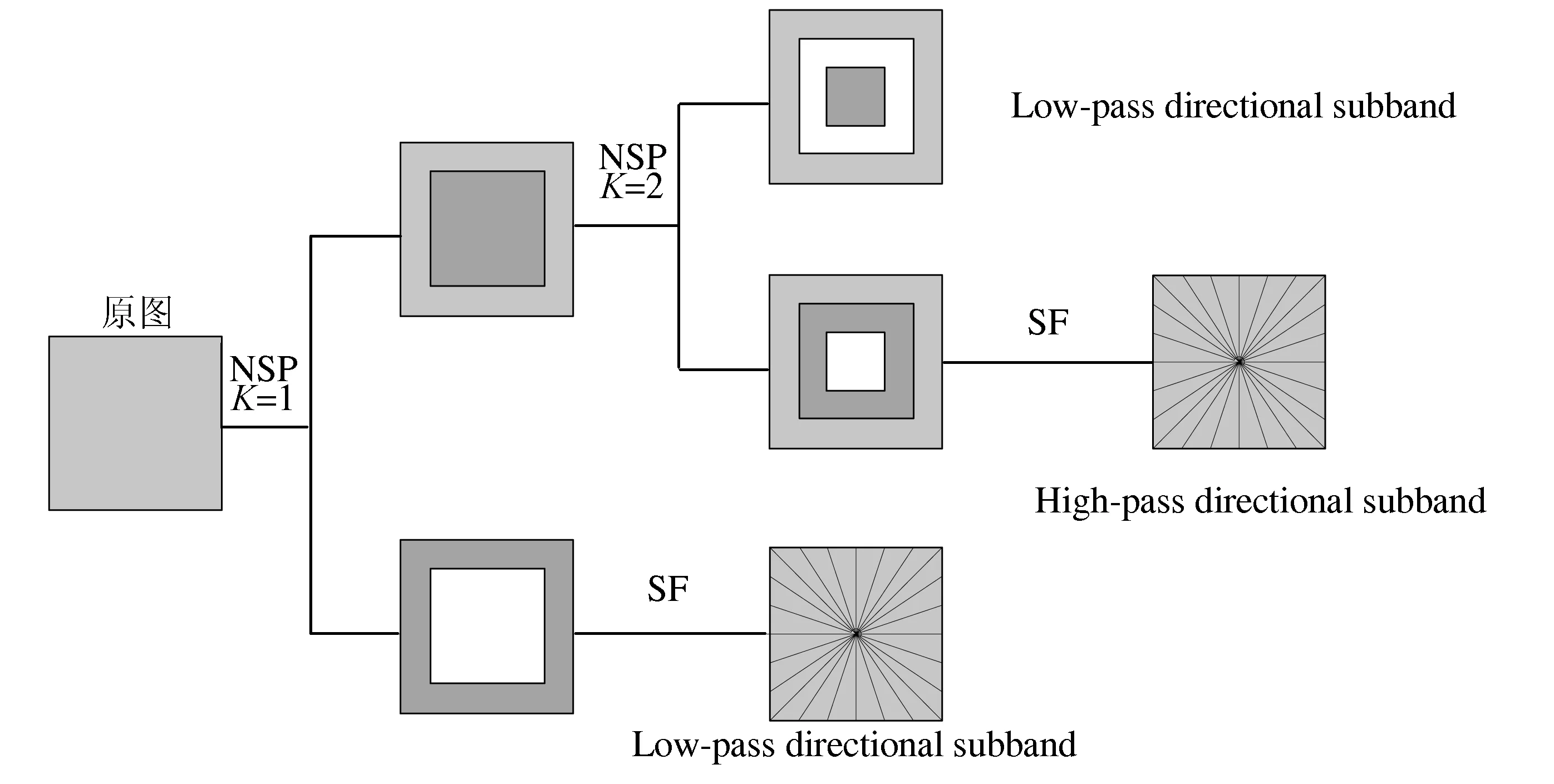
图2 NSST的两层分解过程Fig.2 Two layer decomposition process of NSST

图3 zoneplate 图像的2层NSST变换后的系数图像Fig.3 The coefficient images of the zoneplate image after two level NSST transform

2 基于Cauchy分布模型与NSST变换的图像去噪算法

2.1 最大后验方法估计子带系数

假设含噪声图像经过NSST变换后的系数表示成如下形式：

x=y+n.

其中，y为不含噪声的NSST系数，n为噪声系数.因此可以通过最大后验概率(MAP)方法，最大化ln(y|x)来估计不含噪声的NSST系数y[14]，形式如下：

其中,lnpx|y≈lnpn.

假如噪声为均值为0的高斯白噪声，因此n服从均值为0的高斯分布，即有

其中，σ2为噪声方差，因此只要针对NSST系数进行合适的模型建立，则可估计出不含噪声的系数.

2.2 先验柯西分布模型

自然图像经过NSST变换的系数分布直方图呈现“高尖峰、长拖尾”的形状，且峰值分布在零点处，不符合传统的高斯分布.常用的多尺度系数先验模型有广义高斯分布(GGD)、拉普拉斯分布(Laplacian)和柯西分布(Cauchy)等.其中Cauchy分布是一个含两参数的概率密度模型，其对“长拖尾”的系数分布具有良好的建模效果.

对于系数集X={x1,x2,…,xN}，其Cauchy分布函数的定义为

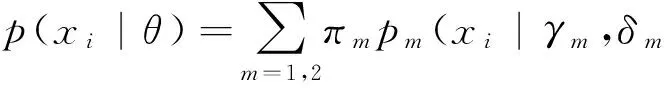
图4 图像系数拟合结果Fig.4 The testing images’ coefficients fitting results

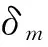
下面分别采用广义GGD分布模型、Laplacian分布模型和Cauchy分布模型对两种不同类型测试图像的NSST子带系数进行精度拟合实验，利用极大似然估计法对参数进行估计，并选取 KS(Kolmogorov-Smirnov)值作为评价指标来判别对NSST子带系数的拟合程度.KS的计算公式为

KS=maxw∈RFh(w)-Fe(w).

其中,Fh(·)和Fe(·)分别为先验概率分布函数和标准分布的累积分布函数.KS越小表明拟合效果越好.图4和表1分别表示了图像的拟合结果以及精度检测结果.

表1 不同分布对图像系数拟合结果

从图4和表1可以看出，对于两种不同类型测试图像的NSST子带系数，Cauchy分布较广义GGD分布和Laplacian分布具有更好的自适应性和拟合效果.可见，在NSST变换域下，Cauchy分布是比广义GDD分布和Laplacian分布拟合精度更好的概率分布函数，因此本文选取Cauchy分布模型对NSST系数进行建模，作为NSST系数的先验模型.

2.3 去噪算法的实现过程

基于柯西分布模型与NSST变换的图像去噪算法总体步骤如下：

Step1 将含噪声图像进行3层NSST分解.

Step2 通过蒙特卡罗方法估计噪声方差，再通过极大似然方法估计先验模型的参数.

Step3 获得不含噪声的NSST子带系数估计.

Step4 将估计得到的子带进行NSST逆变换，获得去噪声图像.

3 实验结果与分析

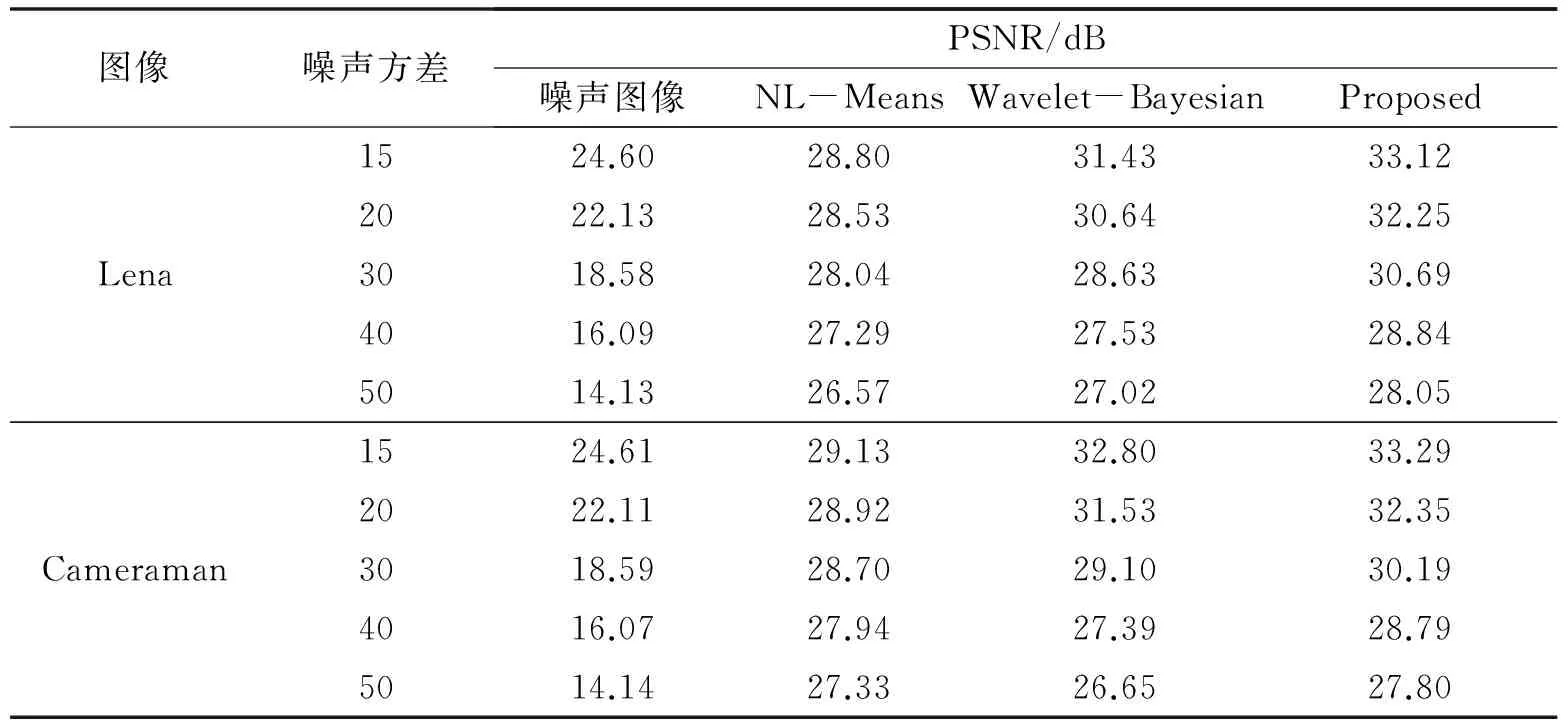
为了验证本文提出方法的有效性，选取North Island，Shedao，Lena和Barara四幅512×512大小的图像进行实验.实验环境为Matlab R2009b.其中，NSST变换选用了“maxflat”非下采样多尺度滤波器和“dmaxflat7”非下采样方向滤波器，分解层数为3，每层子带个数为2，4，8，方向滤波器的分解方向分别为16，32，64.添加的噪声为不同方差的高斯白噪声，实验结果通过去噪图像的主观视觉效果和客观峰值信噪比来(PSNR)评价去噪方法的性能.PSNR定义如下：

表2给出了本文提出方法在不同方差下，与NL-Means[15]方法和Wavelet-Bayesian[16]方法相比较之后的客观评价结果，图5为在噪声方差30的情况下，本文提出的方法与对比方法的去噪主观结果，图6为Lena图像经过4倍放大后的去噪结果.

表2 不同模型去噪方法的PSNR对比

续表

图5 不同去噪方法的去噪图像对比Fig.5 The comparison of the denosing results for different methods

图6 Lena中局部区域放大4倍的去噪图像对比Fig.6 The comparison of the denoising results of the four times partial Lena image

4 结束语

首先对图像NSST域的系数子带系数进行拟合实验，获得Cauchy分布较GGD和Laplacian分布具有更好的自适应性和拟合效果；进一步将Cauchy分布作为图像去噪的先验概率模型，通过最大后验概率方法估计出子带的后验系数.在此基础上，提出一种基于Cauchy分布模型与NSST的图像去噪算法，取得了很好的去噪效果.与文献[16]方法相比，对添加噪声方差为30后的图像噪声，去噪后图像的PSNR平均提高1.93 dB,同时从视觉效果上看，该模型在有效去除噪声的同时，较好地保留了原图像中的边缘和纹理细节信息，特别对纹理复杂、丰富的图像具有一定的优势.

[1] 焦李成，谭山.图像的多尺度几何分析：回顾和展望[J].电子学报,2003,31(12A):1975-1981.

[2] GUO K H,LABATE D.Optimally sparse multidimensional representation using shearlets[J].SIAM Journal on Mathematical Analysis,2007,39(1):298-318.

[3] LAKSHMAN H, LIM W Q, SCHWARZ H, et al.Image interpolation using shearlet based iterative refinement [J].Signal Processing:Image Communication,2015,36(4):83-94.

[4] XU K, LIU S H, AI Y H.Application of Shearlet transform to classification of surface defects for metals[J].Image and Vision Computing,2015,35(3):23-30.

[5] LI Y M, PO L M, XU X Y,et al.No-reference image quality assessment with shearlet transform and deep neural networks[J].Neurocomputing,2015,154:94-109.

[6] GOU K G, LABATE D, LIM W Q.Edge analysis and identification using the continuous shearlet transform[J].Applied and Computational Harmonic Analysis,2009,27(1):24-46.

[7] LIU X, YUE Z, WANG J J.Image fusion based on shearlet transform and regional[J].International Journal of Electronics and Communications (AEÜ),2014,68(6):471-477.

[8] LIU S Q, SHI M Z, HU S H, et al.Synthetic aperture radar image de-noising based on Shearlet transform using the context-based model[J].Physical Communication,2014,13:221-229.

[9] 刘卫华，何明一.基于高斯混合模型图像局部自适应去噪算法[J].系统工程与电子技术,2009,31(12):2806-2808.

[10] 王智文,李绍滋.基于多元统计模型的分形小波自适应图像去噪[J].计算机学报,2014,37(6):1380-1388.

[11] 付国庆.基于NSCT域各向异性双变量萎缩图像去噪[J].电子设计工程,2012,20(18):178-181.

[12] KUTYNIOK G,LABATE D.Shearlets:multiscale analysis for multivariate data[M].Dordrecht:Springer,2012.

[13] EASLEY G, LABATE D, LIM W Q.Sparse directional image representations using the discrete shearlet transform[J].Applied and Computational Harmonic Analysis,2008,25(1):25-46.

[14] 刘薇,徐凌,杨光.基于双树复小波二元统计模型的图像去噪方法[J].中国图像图形学报,2009,14(7):1291-1297.

[15] BUADES A, COLL B, MOREL J M.A nonlocal algorithm for image denoising[J].IEEE Computer Vision and Pattern Recognition San Diego,2005,2:60-65.

[16] 王相海,刘晓倩,张爱迪,等.曲线拟合确定阈值的非抽取小波贝叶斯图像去噪方法[J].模式识别与人工智能，2016,29(4):322-331.

ImagedenoisingalgorithmbasedonCauchydistributionmodelandNSSTtransform

WANGXianghai1,ZHUYihuan1,GENGDan2,SONGChuanming1

(1.School of Computer and Information Technology, Liaoning Normal University,Dalian 116081,China; 2.School of Mathematics,Liaoning Normal University,Dalian 116029,China)

In order to solve the problem that the multi-scale transform threshold denoising method does not consider the correlation between sub-band coefficients, a denoising method based on statistical model is proposed.The non-downsampling Shearlet transform (NSST) has a good directional sensitivity, anisotropy and translation invariance, which is close to the optimal multi-scale sparse representation.In this paper, the effectiveness of the Cauchy distribution model as a priori probability model is analyzed.An image denoising algorithm based on the Cauchy distribution model and NSST transform is proposed. The statistical model denoising method based on wavelet and NSST transform based on Laplacian distribution Denoising method are compared.The simulation results show that the presently proposed method has better denoising effect.

non-subsampling Shearlet;Cauchy distribution model;maximum a posteriori probability;image denoising

王相海(1965- )，男，吉林汪清人，辽宁师范大学教授,博士，博士生导师,CCF高级会员.

TP391

:A

2017-04-27

国家自然科学基金资助项目(41671439；61402214)；高等学校博士学科点专项科研基金资助项目(20132136110002)；大连市科学技术基金资助项目(2013J21DW027)

1000-1735(2017)03-0324-08

10.11679/lsxblk2017030324