二维对流扩散方程逆过程的最小二乘支持向量机求解
吴自库,陈建毅
(青岛农业大学理学与信息科学学院,山东 青岛 266109)
二维对流扩散方程逆过程的最小二乘支持向量机求解
吴自库,陈建毅
(青岛农业大学理学与信息科学学院,山东 青岛 266109)
利用最小二乘支持向量机方法求解了二维对流扩散方程逆过程.相对于已有的反问题研究方法,本方法具有简单、实用、稳定性好等诸多优点.数值结果表明最小二乘支持向量机方法可有效地求解二维对流扩散方程逆过程,并且具有较高的精度和稳定性.
二维对流扩散方程;逆过程;最小二乘支持向量机;近似解
二维对流扩散方程是一类具有广泛应用的数学物理方程.它可以描述许多物理现象,例如污染物的扩散、海水的盐度、交通流等.近年来二维对流扩散方程反问题成为研究热点之一,研究较多的主要有逆过程反问题、源项反问题、模型参数估计.[1-4]
现阶段一些学者利用软计算方法解微分方程及其相关问题,常用的方法有人工神经网络方法(ANN)、最小二乘支持向量机方法(LS-SVM)等.其原理是利用基核函数逼近问题的解,将问题转化为二次优化问题.Lagaris等[5-6]利用人工神经网络方法研究了常微分方程和偏微分方程.Baymani等[7]研究了Stokes方程的解.最近Mehrkanoon等[8-9]利用最小二乘支持向量机方法研究了常微分方程及其相关问题,取得了令人满意的结果.吴自库等[10-11]利用最小二乘支持向量机方法研究了一维热传导热源反问题和一维对流扩散过程逆过程反问题.本文利用最小二乘支持向量机方法研究二维对流扩散过程逆过程反问题.
1 最小二乘支持向量机方法简介
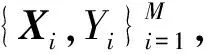
(1)
这里K为基核函数,αi和b为回归参数.最小二乘支持向量机原理就是将估计回归参数问题转化为如下的二次规划问题:
(2)
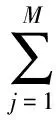
(3)
其中γ∈R+为惩罚因子,ei∈R为偏差项,αT=(α1,α2,…,αM),eT=(e1,e2,…,eM).
问题(2)和(3)的拉格朗日函数为
(4)
这里ηi是拉格朗日乘子.依据最优性条件(KKT条件)有
(5)
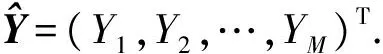
2 二维对流扩散方程逆过程最小二乘支持向量机求解机制
考虑如下问题:
(6)
这里dx、dy、κ和c为模型参数,f1、f2、g1、g2和g为已知函数.
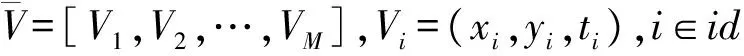
取方程(6)如下形式的近似解:
(7)
B(x,y,t)=(1-t)(x-x2)(y-y2);
(8)
A(x,y,t)=A1(x,y,t)+A2(x,y,t),
(9)
A1(x,y,t)=(1-x)f1(y,t)+xf2(y,t)+(1-y)[g1(x,t)-(1-x)g1(0,t)-xg1(1,t)]+y[g2(x,t)-(1-x)g2(0,t)-xg2(1,t)],
(10)
A2(x,y,t)=t[g(x,y)-A1(x,y,1)].
(11)
将(7)式代入(6)式得
(12)
其中:
F(V)=cB(V)+Bt(V)+dxBx(V)+dyBy(V)-κ(Bxx(V)+Byy(V));
G(V)=cA(V)+At(V)+dxAx(V)+dyAy(V)-κ(Axx(V)+Ayy(V))-f(V);
E(V,Vj)=E1(V,Vj)+E2(V,Vj)+E3(V,Vj),
E1(V,Vj)=[Bt(V)+cB(V)+dxBx(V)+dyBy(V)-k(Bxx(V)+Byy(V))]K(V,Vj),
E2(V,Vj)=B(V)(Kt(V,Vj)+dxKx(V,Vj)+dyKy(V,Vj))- 2κ(Bx(V)Kx(V,Vj)+By(V)Ky(V,Vj)),
E3(V,Vj)=-κB(V)(Kxx(V,Vj)+Kyy(V,Vj)).
为了求得回归参数,依据LS-SVM原理将参数回归问题转化为如下二次规划问题:
(13)
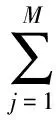
(14)
其中(13)式为目标函数,(14)式为约束条件,γ∈R+为正则化参数,ei是偏差项.上述优化问题的拉格朗日函数为
(15)
依据最优性条件(KKT)有
(16)
消去偏差项ei得到如下回归方程:
(17)
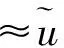
3 参数调节机制及稳定性分析
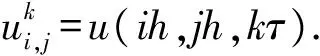
(18)
(19)
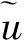
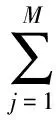
(20)
故可以将‖Lu(V)‖∞作为衡量该方法解的稳定性和精度的指标.由于Lu(V)为一致连续可微函数,且在边界上为零,因而‖Lu(V)‖∞在内部取得.不妨令
‖Lu(V)‖∞=|Lu(x*,y*,t*)|,(x*,y*,t*)∈(0,1)3,
(21)
令距离(x*,y*,t*)最近的样本点为V*=(xI,yI,tI),于是有
‖Lu(V)‖∞=|Lu(x*,y*,t*)-Lu(V*)+Lu(V*)|≤ |Lu(x*,y*,t*)-Lu(V*)|+|Lu(V*)|≤(Mx+My)h+Mtτ+‖e‖∞.
(22)
这里Mx=‖Lux(V)‖∞,My=‖Luy(V)‖∞,Mt=‖Lut(V)‖∞.由(22)式可知本算法是收敛且稳定的.
4 数值例子
以两个典型的例子验证利用最小二乘支持向量机方法求解二维对流扩散方程逆过程反问题的有效性.在数值实验中令步长h=0.1,样本点的个数M=729.
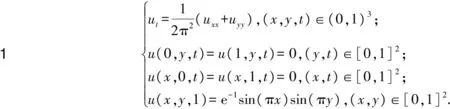
(23)
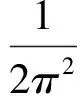
u(x,y,t)=e-tsin(πx)sin(πy).
(24)
反演的初始条件为
w(x,y)=u(x,y,0)=sin(πx)sin(πy).
(25)
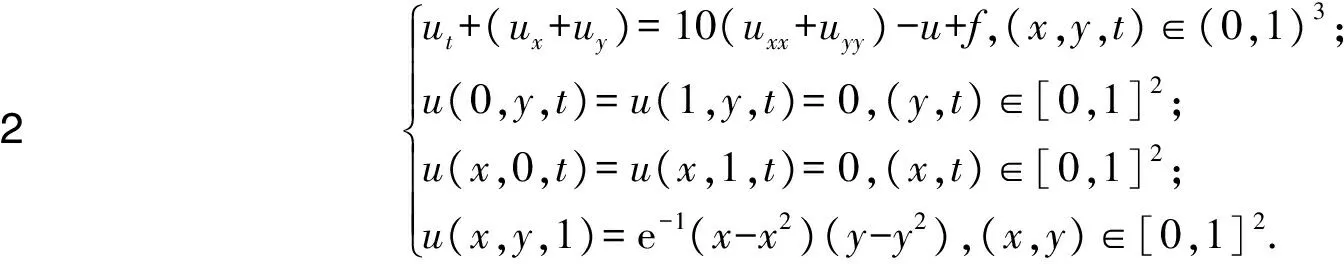
(26)
这里f(x,y,t)=e-t[21(x+y-x2-y2)+2xy(x+y)],c=1,dx=dy=1,κ=10.其解析解为
u(x,y,t)=e-t(x-x2)(y-y2).
(27)
反演的初始条件为
w(x,y)=u(x,y,0)=(x-x2)(y-y2).
(28)
数值实验中参数σ的优化值及反演结果误差见表1.图1为例1的初始条件反演结果,左图为反演的u(x,y,0)曲面,右图为u(x,y,0)的解析解与近似解的误差曲面.图2为例2的相应结果.数值实验结果说明最小二乘支持向量机方法能较好地求解二维对流扩散方程逆过程,而且本方法将问题最终转换为仅含一个调节参数的线性方程组,可操作性强,避免了繁琐的积分、微分运算.

表1 LS-SVM数值仿真结果
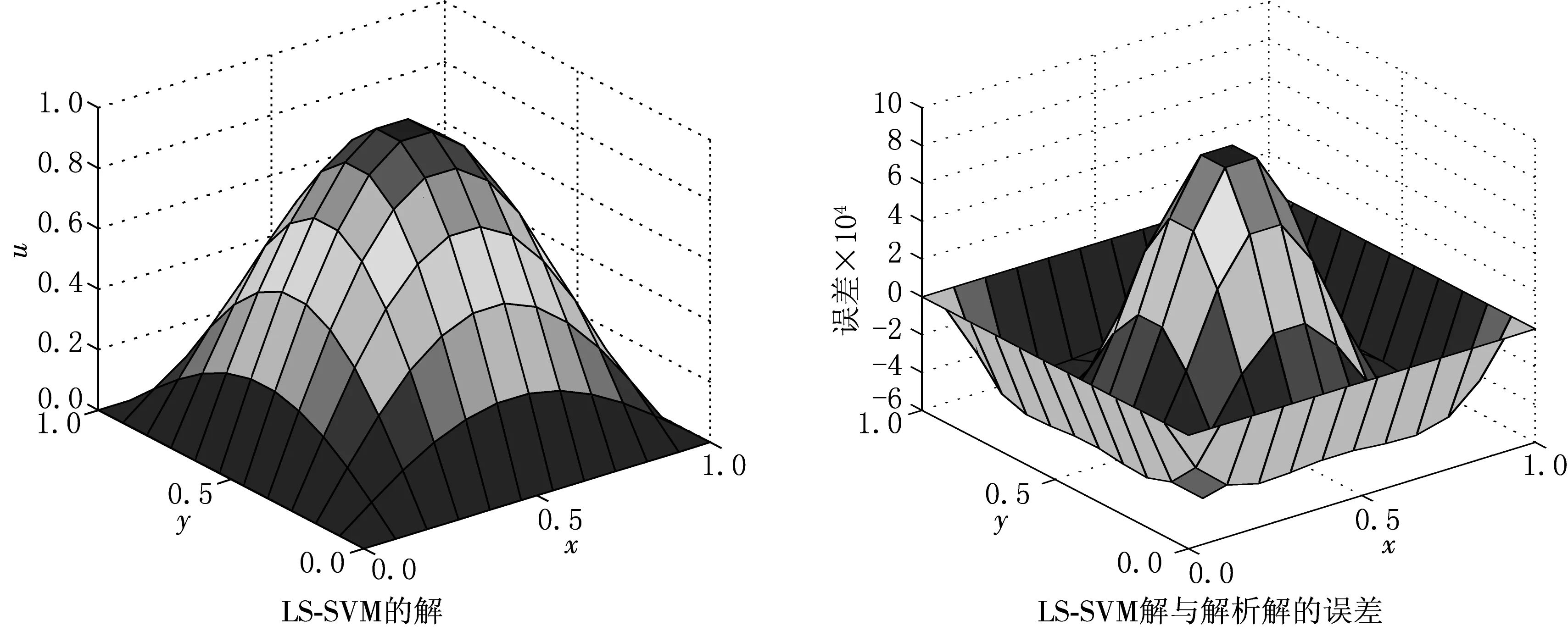
图1例1初始条件u(x,y,0)数值反演结果
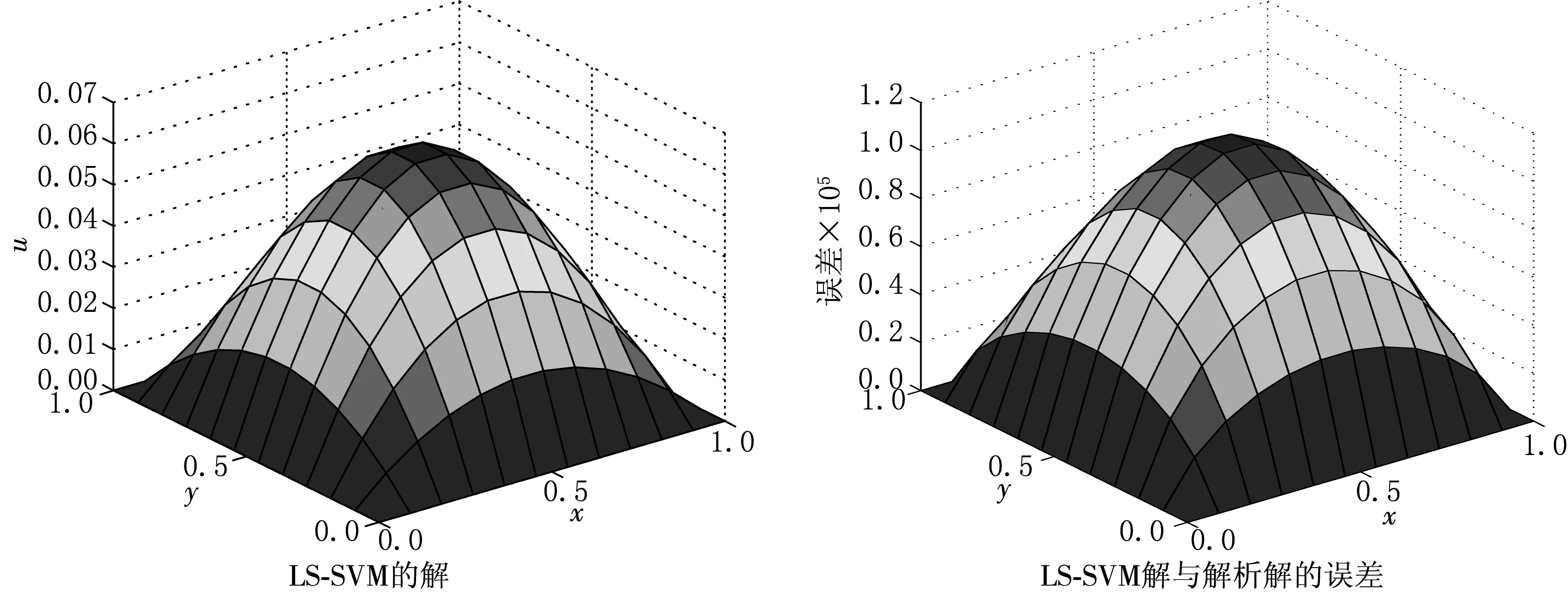
图2 例2初始条件u(x,y,0)数值反演结果
5 结论
本文利用LS-SVM法研究了二维对流扩散方程逆过程反问题,推导了反演初始条件的公式,给出了初始条件的半解析解表达式.同其他方法相比,这种方法具有理论完备、处理边界条件灵活、抛开了繁琐的微分运算等优点.数值实验结果显示该方法能成功地反演出二维对流扩散方程逆过程的初始条件,并具有较高的精度和较好的稳定性.该方法完全可以应用于更复杂的偏微分方程反问题的研究中.其求解偏微分方程反问题的机制就是将原问题转换为含有1个调节参数的线性方程组,利用基核函数一致逼近问题的解.此外,这里采用的LS-SVM法更为简洁实用,不需要考虑对偶形式.然而,由于本问题的核心是估计近似解的回归参数α和b,因而对于非线性偏微分方程反问题理论上可行,但实际操作难度大,这也是本文选择线性偏微分方程反问题的主要原因.
[1] 周康,毛献忠,李子.污染物二维非恒定输运初值反问题研究[J].水利发电学报,2014,33(4):118-125.
[2] 陈亚文,周雪文.二维非稳态对流扩散方程反问题的混沌粒子群算法[J].西安工业大学学报,2011,31(5):470-473.
[3] 朱嵩,刘国华,毛根海,等.利用贝叶斯推理估计二维含源对流扩散方程参数[J].四川大学学报(工程科学版),2008,40(2):38-43.
[4] 闵涛,刘相国,张海燕,等.二维稳态对流-扩散方程参数反演的迭代算法[J].水动力学研究与进展,2007,22(6):744-752.
[5] LAGARIS I E,LIKAS A,FOTIADIS D I.Artificial neural networks for solving ordinary and partial differential equations [J].IEEE Trans Neural Networks,1998,9(5):987-1000.
[6] LAGARIS I E,LIKAS A,PAPAGEORGIO D G.Neural-network methods for boundary value problems with irregular boundaries [J].IEEE Trans Neural Networks,2000,11(5):1041-1049.
[7] BAYMANI M,KERAYECHIAN A,EFFAI S.Artificial neural networks approach for solving Stokes problem [J].Applied Mathematics,2010(1):288-292.
[8] MEHRKANOON S,SUYKENS J A K.LS-SVM approximate solution to linear time varying descriptor systems [J].Automatica,2012,48(10):2502-2511.
[9] MEHRKANOON S,FALCK T,SUYKENS J A K.Approximate solution to ordinary differential equations using least squares support vector machines [J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(9):1356-1367.
[10] 吴自库,李福乐,郭渡溁.一维热传导热源反问题基于最小二乘法的正则化方法[J].计算物理,2016,33(1):98-103.
[11] 吴自库,许海洋,李福乐.一维对流扩散方程逆过程LS-SVM解[J].黑龙江大学学报(自然科学版),2016,33(4):429-434.
[12] VAPNIK V N.The nature of statistical learning theory [M].New York:Springer-Verlag,1995:28-88.
[13] SUYKENS J A K,VANDEWALLE J.Least squares support vector machine classifiers [J].Neural Process Letter,1999,9(3):293-300.
(责任编辑:李亚军)
2-Dconvection-diffusionequationinverseprocessbasedonleastsquaresupportvectormachinesmethod
WU Zi-ku,CHEN Jian-yi
(Science and Information College,Qingdao Agricultural University,Qingdao 266109,China)
Least square support vector machines method is used to solve 2-Dconvection-diffusion equation inverse process.The method used here has many advantages compared with the other methods,such as simple,practical and good stability.This method has been successfully tested on practical examples and has yielded higher accuracy and stability.
2-Dconvection-diffusion equation;inverse process;least square support vector machines;approximate solution
1000-1832(2017)03-0047-05
10.16163/j.cnki.22-1123/n.2017.03.011
2016-01-14
国家自然科学基金资助项目(61403233);山东省教育厅科技计划项目(J09LA12).
吴自库(1968—),男,博士,教授,主要从事偏微分方程反问题研究.
O 242 [学科代码] 110·47
A

