基于改进谱修正迭代法的数值保角变换计算法

吕毅斌，赖富明，王樱子，武德安

(1.昆明理工大学理学院，云南 昆明 650500； 2.昆明理工大学计算中心，云南 昆明 650500； 3.电子科技大学数学科学学院，四川 成都 611731)

基于改进谱修正迭代法的数值保角变换计算法

吕毅斌1，赖富明1，王樱子2，武德安3

(1.昆明理工大学理学院，云南 昆明 650500； 2.昆明理工大学计算中心，云南 昆明 650500； 3.电子科技大学数学科学学院，四川 成都 611731)

通过改进的谱修正迭代法，计算基于模拟电荷法的双连通区域数值保角变换的约束方程，得到了新的电荷点和变换半径，构造了近似保角变换函数.进而提出了新算法，并通过数值实验检验了新算法的有效性.

数值保角变换；双连通区域；模拟电荷法；谱修正迭代法

0 引言

保角变换的理论来源于复变函数论，其在电磁理论、电场与热场理论、流体力学等许多领域均有广泛应用.[1-3]保角变换的主要求解方法有解析法和数值法.解析法的基础是Riemann存在唯一性定理，它指出任意一个边界多于一点的单连通区域总存在一个解析函数将其映射为单位圆盘.类似地，对于双连通区域也存在一个解析函数将其映射成同心圆.Riemann存在唯一性定理证明了变换函数的存在性，但却不能给出变换函数的具体表达式.相比于解析法，保角变换的数值法在解决实际工程问题的过程中具有独特的优势，因此吸引许多学者对其做了大量研究.目前，保角变换的数值法主要有积分方程式法[4-6]、正交多项式法[7]和模拟电荷法[8-10].基于模拟电荷法的数值保角变换计算法是由日本数学家Amano提出来的，它具有计算简单、不用数值积分、计算精度高等优点.然而，Amano并没有给出求解基于模拟电荷法的双连通区域保角变换约束方程的具体算法.

本文针对以椭圆为边界的双连通区域，给出了模拟电荷点和约束点，进而构造了约束方程.对约束方程进行分析，发现其是病态非奇异的.针对这一特性，采用改进的谱修正迭代法[11-12]对其进行求解，计算得到新的电荷点和变换半径，从而构造了高精度的近似保角变换函数.相比于条件预优法、投影法、刚性常微分方程法等求解方法，改进的谱修正迭代法能很好地改善方程组的病态性，且计算结果也是无偏的，适合于计算良态、病态和秩亏方程.最后，在改进的谱修正迭代法的基础上，通过等高线模拟了双连通区域数值保角变换的计算结果.

1 基于模拟电荷法的双连通区域数值保角变换计算法[13-17]

设D为Z平面上由曲线C1和C2围成的有限双连通区域，通过基于模拟电荷法的保角变换将之映射为W平面的一个圆环μ<|w|<1，C1和C2分别是外部和内部边界(见图1).

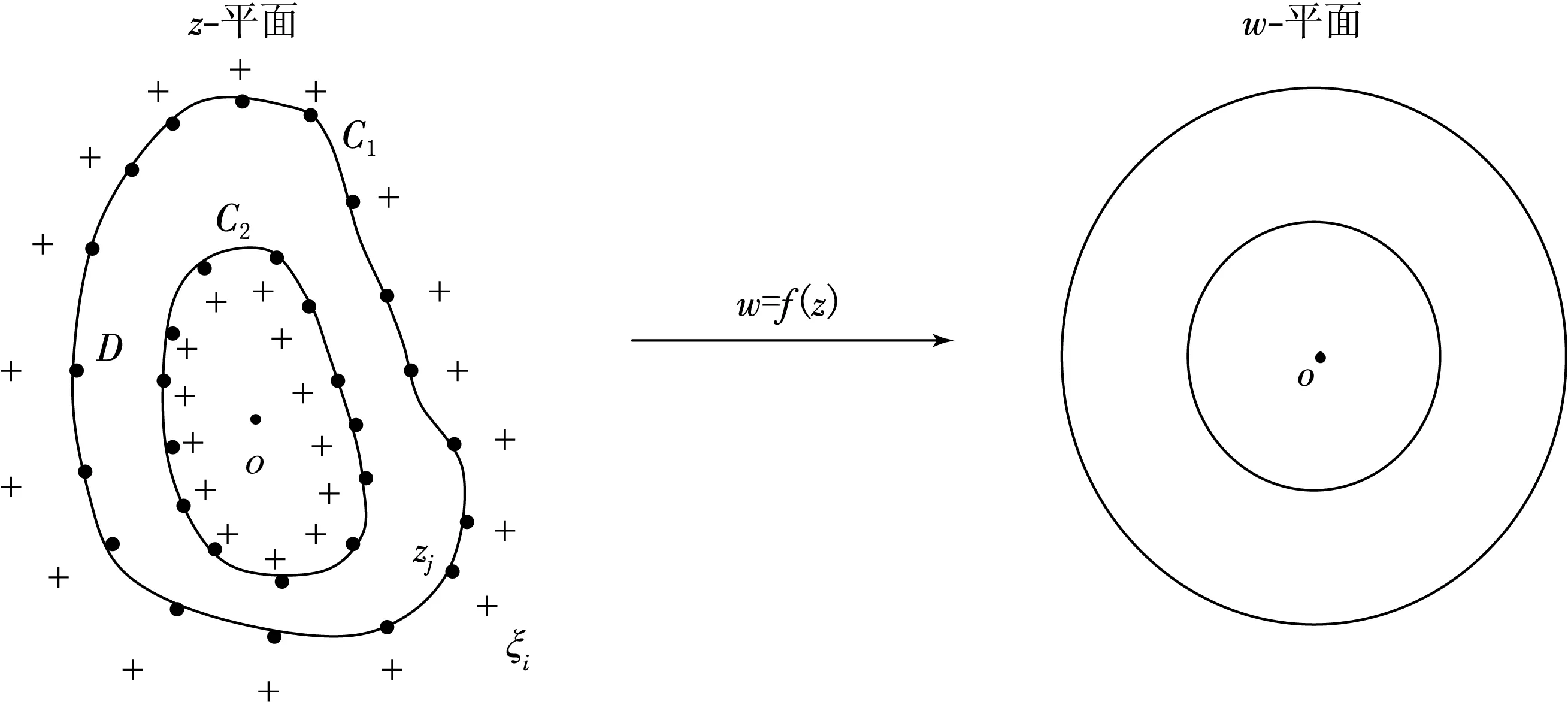
(+表示模拟电荷点，·表示约束点)

不失一般性，假定f(0)=0.当f(z)满足正规化条件f(∞)=∞，f′(∞)>0时，f(z)可以表示成

(1)

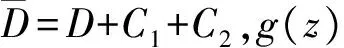
(2)

h(z)和g(z)为共轭调和函数，根据模拟电荷法，h(z)和g(z)可以分别由

(3)

(4)

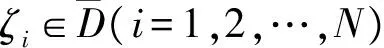
(5)

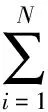
(6)

(7)

联立(5)—(7)式，得到以Qi(i=1，2，…，N)和logM为未知量的线性方程

(8)

其中系数矩阵中的一般项aij=log|zj-ζi|.

最后，利用zi，ζi，Qi，M计算双连通区域的数值保角变换.

2 改进的谱修正迭代法在双连通区域数值保角变换上的应用

方程(8)称为基于模拟电荷法的双连通区域数值保角变换的约束方程，简称为约束方程.将其写成标准线性方程的形式

Ax=b，

(9)

其中A∈R(N+1)×(N+1)，x∈RN+1，b∈RN+1，N表示模拟电荷点数.由于cond(A)=‖A‖‖A‖-1较大且det(A)≠0，因此方程(9)是病态非奇异的，b的微小扰动会引起解x的很大变化，从而不能得到高精度的未知电荷Q1，Q2，…，QN和保角变换半径M.

改进的谱修正迭代法[18]能够很好地改善上述方程的病态性.对方程(9)进行预处理，两边同时乘以AT有

ATAx=ATb，

(10)

其中ATA是对称正定的.显然x=(ATA)-1ATb，但是cond(ATA)很大，因此对ATA求逆会不稳定.

为克服这一缺点，假定E是(N+1)×(N+1)的单位矩阵，在(10)式的两边同时加上μx，得到

(ATA+μE)x=ATb+μx，

(11)

其中μ为修正因子(0<μ<1).进一步得到改进的谱修正迭代法的迭代公式

xk=(ATA+μE)-1(ATb+μxk-1).

(12)

另一方面，迭代(12)式可以改写成

xk=μ(ATA+μE)-1xk-1+(ATA+μE)-1ATb.

(13)

设x*为约束方程的精确解，那么x*=μ(ATA+μE)-1x*+(ATA+μE)-1ATb.根据(13)式，

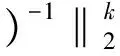
(14)

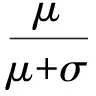
表1 改进的谱修正迭代算法

表1中，MaxIter和SolRD分别表示最大迭代次数和相对误差.ATA+μE为对称正定矩阵，所以可以按LDLT分解，其中L为单位下三角矩阵，D为对角矩阵.LDLT分解大约需要n3/6次乘除法，大约是直接LU分解法计算量的一半.相比于LTL分解，LDLT分解不需要开方计算，使得结果精度更高.[19]

综合前面的分析，基于改进的谱修正迭代法的双连通数值保角变换计算法分为以下几步：

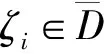
步骤2 构造约束方程，利用改进的谱修正迭代法计算约束方程(见表1)，得到电荷Q1，Q2，…，QN和保角变换半径M.

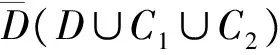
3 数值实验

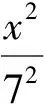
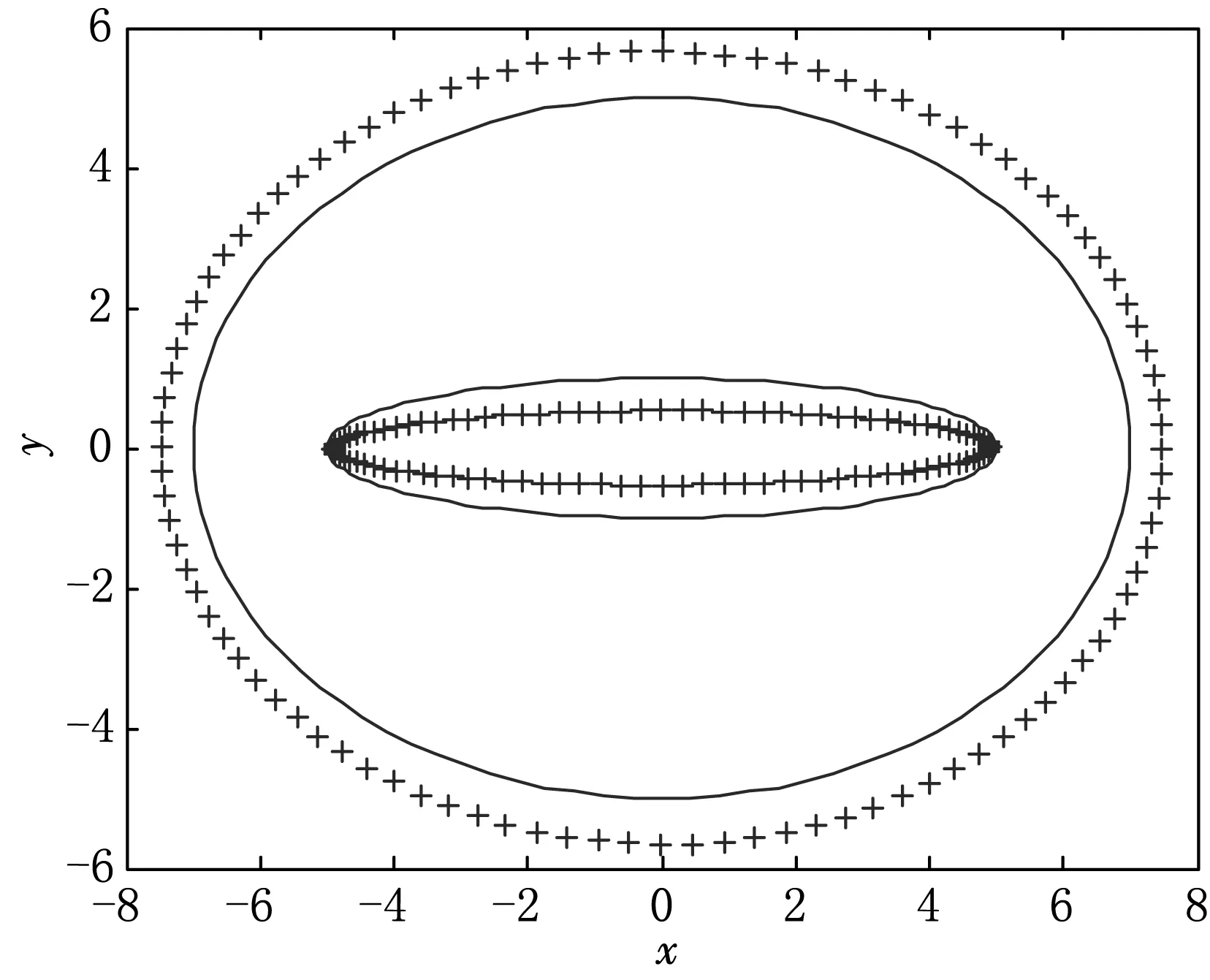
图2 双连通区域模拟电荷点分布

图3 误差曲线

根据前面求出的电荷和保角变换半径，可构造近似保角变换函数f(z).取区域D的等高线，如图4，其中粗实线代表边界C1和C2，细线代表等高线.图5表示由近似保角变换函数映射后得到的图像，从中可以看出，边界C1和C2变换后的图像为同心圆，等高线与边界组成的内部区域仍然对应同心圆围成的内部区域.进一步证明了基于改进谱修正迭代法的双连通区域数值保角变换计算法的有效性.

图4 区域及其等高线

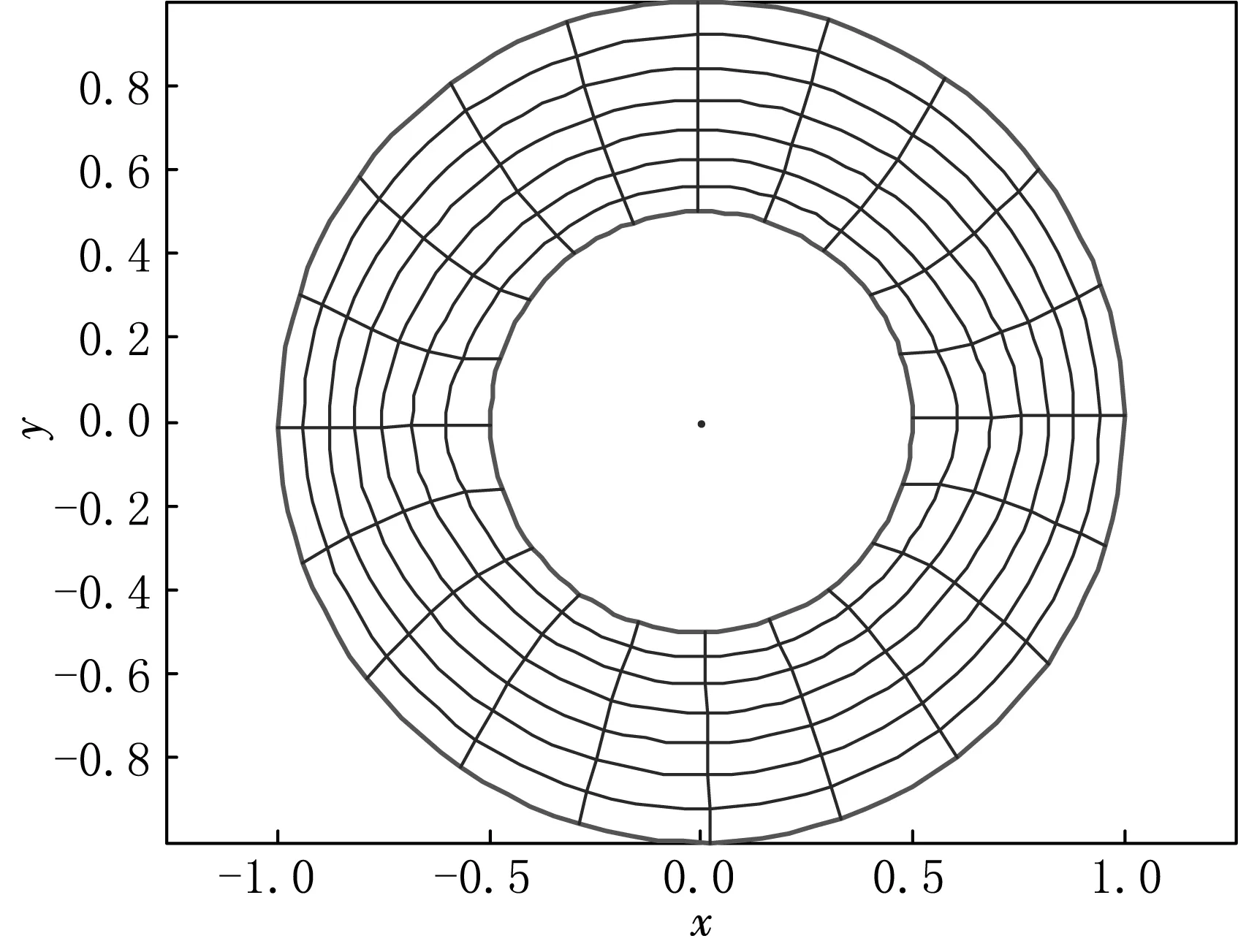
图5 区域及其等高线的保角变换

4 结论

本文提出了一种求解双连通区域数值保角变换约束方程的新算法，并通过数值实验验证了新算法的可行性.利用新方法得到的数值保角变换的精度比较高，且通过等高线模拟了双连通区域数值保角变换的计算结果.这种方法同样可考虑用于多连通区域的数值保角变换.

[1] 林为干.微波理论与技术[M].北京：科学出版社，1979：64-120.

[2] 曹伟杰.保形变换理论及其应用[M].上海：上海科学技术文献出版社，1988：193-231.

[3] 朱满座.数值保角变换及其在电磁理论中的应用[D].西安：西安电子科技大学，2008.

[4] SYMM G T.An integral equation method in conformal mapping[J].Numer Math，1966，9(3)：250-258.

[5] SANGAWIA A W K，MURIDA A H M，NASSERD M M S.Linear integral equations for conformal mapping of bounded multiply connected regions onto a disk with circular slits[J].Appl Math Comput，2011，218(5)：2055-2068.

[6] SYMM G T.Conformal mapping of doubly-connected domains[J].Numer Math，1969，13(5)：448-457.

[7] KOKKINOS C A，PAPAMICHAEL N，SIDERIDIS A B.An orthonormalization method for the approximate conformal mapping of multiply-connected domains [J].IMAJ Numer Anal，1990，9：343-359.

[8] AMANO K.Numerical conformal mappings of exterior domains based on the charge simulation method [J].Trans Inform Process Soc Japan，1998，29(1)：62-72.

[9] AMANO K.Numerical conformal mappings of interior domains based on the charge simulation method [J].Trans Inform Process Soc Japan，1988，29(7)：697-699.

[10] AMANO K.Numerical conformal mapping of doubly-connected domains based on the charge simulation method [J].Trans Inform Process Soc Japan，1988，29(7)：914-919.

[11] 王新洲，刘丁酉.最小二乘估计中法方程的迭代解法[J].湖北民族学院学报(自然科学版)，2002，20(3)：1-4.

[12] 刘斌，龚健雅，江万寿，等.基于岭参数的谱修正迭代法及其在有理多项式参数求解中的应用[J].武汉大学学报(信息科学版)，2012，37(4)：399-402.

[13] 郑志强.单位圆到任意曲线保角变换的近似计算方法[J].应用数学和力学，1992(5)：449-457.

[14] AMANO K.A charge simulation method for the numerical conformal mapping of interior，exterior and doubly-connected domains [J].Journal of Computational and Applied Mathematics，1994，53：354-361.

[15] LU Y，WU D，WANG Y，et al.The accuracy improvement of numerical conformal mapping using the modified Gram-Schmidt method [M]//QI E R，SHEN J，DOU R L.The 19th International Conference on Industrial Engineering and Engineering Management.Berlin：Springer，2013：555-563.

[16] 姚国梅，吕毅斌，王樱子.数值保角变换的新算法[J].价值工程，2014，31：308-310.

[17] 代荣恒，吕毅斌，王樱子.基于LMS法的数值保角变换计算法[J].曲阜师范大学学报(自然科学版)，2015，41(5)：23-27.

[18] 潘朝毅.谱修正法的收敛分析及其改进[J].四川教育学院学报，2009，25(5)：112-113.

[19] GOLUGB G H，VAN LOAN C F.Matrix computations[M].Baltimore：The Johns Hopkins University Press，2012：153-165.

(责任编辑：李亚军)

Theimprovementofiterationmethodbycorrectingcharacteristicvaluesfornumericalconformalmapping

LU Yi-bin1，LAI Fu-ming1，WANG Ying-zi2，WU De-an3

(1.Faculty of Science，Kunming University of Science and Technology，Kunming 650500，China； 2.Computer Center，Kunming University of Science and Technology，Kunming 650500，China； 3.School of Mathematical Science，University of Electronic Science and Technology，Chengdu 611731，China)

A new method for numerical conformal mapping of doubly-connected domain is considered.This method calculates the constraint equations of numerical conformal mapping based on charge simulation method of doubly-connected domain using the improvement of iteration method by correcting characteristic values，and the approximate conformal mapping function is constructed using new charge points and conformal mapping radius.The efficiency of the proposed method is illustrated by some numerical results.

numerical conformal mapping；doubly-connected domain；charge simulation method；the iteration method by correcting characteristic values

1000-1832(2017)03-0042-05

10.16163/j.cnki.22-1123/n.2017.03.010

2015-12-02

国家自然科学基金资助项目(11461037).

吕毅斌(1972—)，男，副教授，主要从事科学计算与图像处理研究；通信作者：王樱子(1972—)，女，硕士，讲师，主要从事科学计算与数学应用软件设计研究.

O 241 [学科代码] 110·6199

A