基于Clayton Copula函数的 金融高频数据极小值相依性
霍俊爽,张若东,潘淑霞,邰志艳,董小刚
(1.吉林医药学院数学教研室,吉林 吉林 132013; 2.长春工业大学基础学院,吉林 长春 130012)
基于Clayton Copula函数的 金融高频数据极小值相依性
霍俊爽1,张若东1,潘淑霞1,邰志艳1,董小刚2
(1.吉林医药学院数学教研室,吉林 吉林 132013; 2.长春工业大学基础学院,吉林 长春 130012)
基于Clayton Copula函数对股指期货IF1112指数和上证000001指数5 min极小值收益率序列的相依性进行了研究,深入探讨了其下尾部微观结构的相依性.
Copula函数;Clayton Copula函数;相依性
随着经济金融全球化进程的深入,金融市场间的相依性越来越密切.一个金融市场突发的剧烈波动常常也会引起其他金融市场的波动.本文将以高频数据为研究对象,通过分析不同金融市场高频数据极值收益率的变化研究其相依性,从而为金融资产的管理和风险控制提供理论依据.
由于金融市场收益率的分布大多是偏态的,而阿基米德族Copula函数在研究这类金融数据的相依性时有明显优势.本文借助阿基米德族二元Clayton Copula函数研究了股指期货和股指现货市场高频数据极值的相依性.
1 模型方法与参数估计
1.1 Clayton Copula函数与相依性分析
阿基米德Copula函数族包含了多个Copula函数,Gumbel、Clayton、Frank、C Copula等函数是常用的二元阿基米德Copula函数.阿基米德 Copula 函数的定义是由Genest和Mackay 给出的.Clayton Copula函数对变量分布下尾部的变化十分敏感,能够准确反映下尾部相关的变化.[1-3]

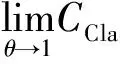
Clayton Copula函数的概率密度函数同样是非对称的,呈“L”形分布,其上尾部低下尾部高的形态与Gumbel Copula函数相反.它对变量分布下尾部的变化十分敏感,能够准确反映下尾部的相关变化,从而对熊市时金融市场之间的波动变化规律有较好描述.若两个随机变量间的相关结构能用Clayton Copula函数来描述,则在分布的下尾部有较强的相关性,而变量在分布的上尾部是渐近独立的.
1.2ClaytonCopula函数的参数估计
Clayton Copula函数参数估计的主要方法有极大似然估计、边际分布推导法、经验Copula法、Kendall系数法等.Rivest和Genest给出了Kendall系数法,推导出了用Kendall系数τ表示阿基米德族Copula函数中参数估计量的方法.[6]
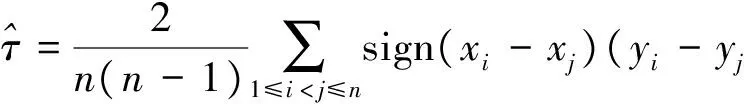
1.3ClaytonCopula模型的检验
Clayton Copula函数及其边缘分布的常用检验方法有卡方检验、K-S检验和分位数-分位图检验(Q-Q图检验).Q-Q图检验是由变量的指定分布与变量的实际分布两组样本的分位数组成.当对应两组样本的分位数近似相等时,其对应的Q-Q图呈一条直线,则拟合较好;反之,若Q-Q图越偏离直线,则拟合的效果就越差.但Q-Q图检验要求必须是大样本,否则结果不准确.[7]
1.4 尾部相依性
尾部相依性主要反映了当一个随机变量X大幅度变化时,另一随机变量Y也发生大幅度变化的概率.由于金融时间序列具有尖峰厚尾的特点,所以在金融分析时研究随机变量的尾部相依性是非常重要的.Clayton Copula函数恰好能反映出当一个随机变量暴涨或暴跌时,另一随机变量也发生暴涨或暴跌的概率.
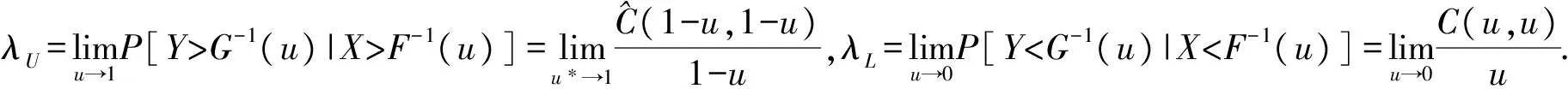
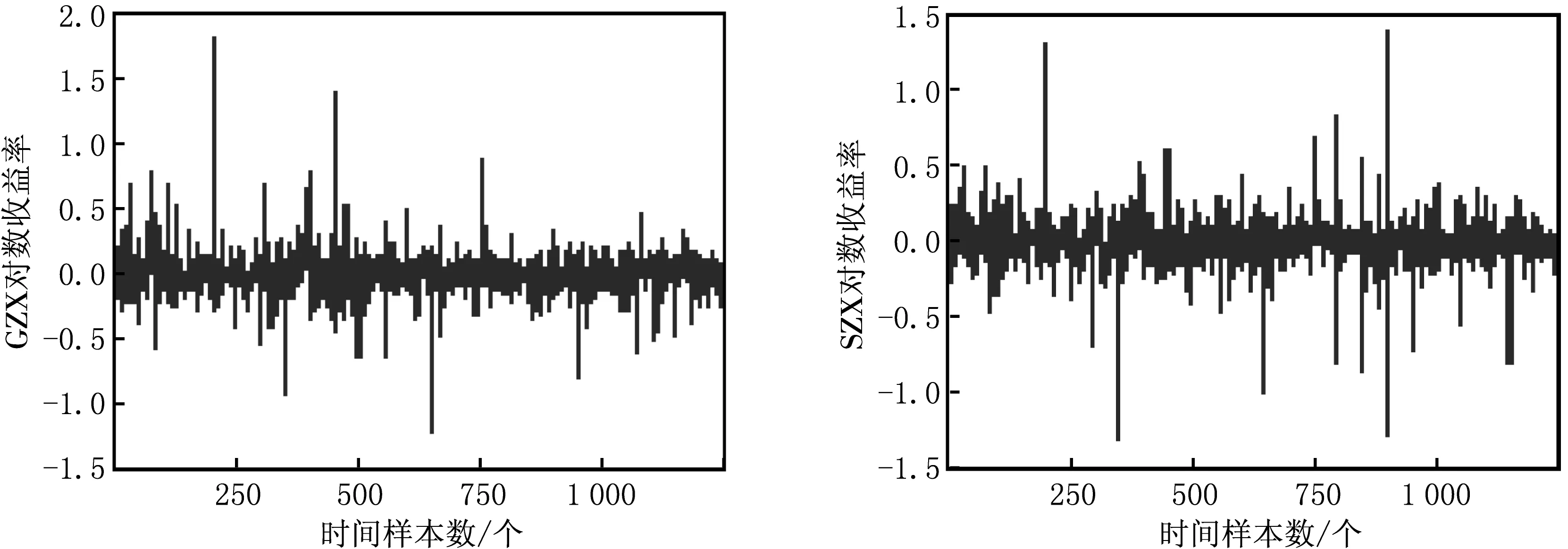
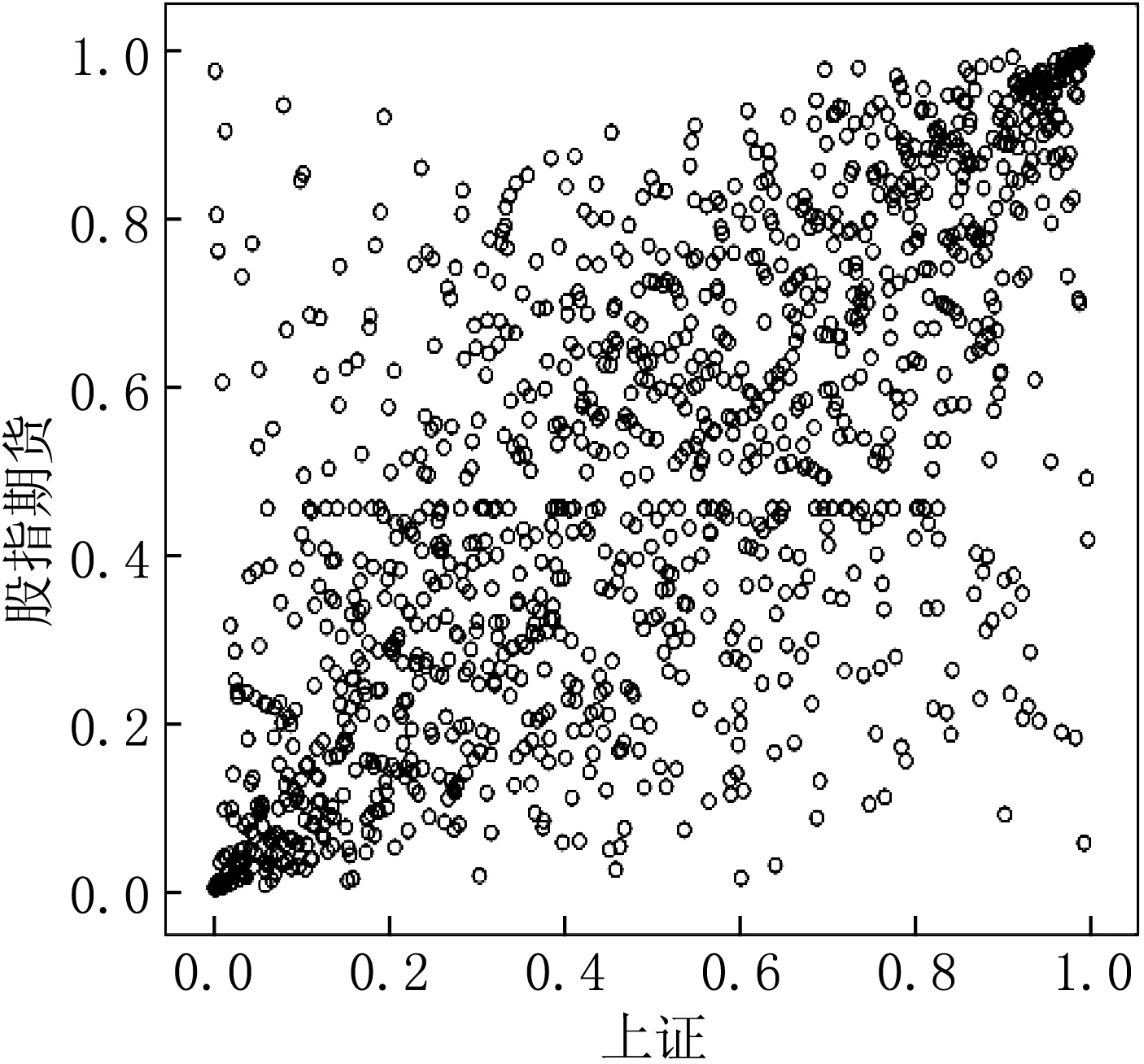
根据Clayton Copula函数的定义和性质,可以推导出Clayton Copula函数的表达式.正尾部相依性λU(α)=P(Y>qα|X>qα)=(1-2α+c(α,α))/(1-α);负尾部相依性λL(α)=P(Y 主要研究将指数波动转化为收益率的数据.数据选取的时间为2011年10月24日至2011年11月18日,数据选取的对象是股指期货IF1112指数的5 min内最小值(GZX)和上证指数的5 min内最小值(SZX).价格定义为每5 min内指数的最小值PT,对数收益率定义为rt=100ln(Pt/Pt-1).选取该时间段内同期交易的1 200对数据构成两个序列,应用Eviews,SPSS,Matlab等软件计算和绘图. 2.1 极小值收益率序列的波动图 使用Eviews软件计算了收益率,并绘制了极值收益率序列的波动图,见图1. 图1 GZX和SZX收益率序列波动图 图1中两图纵坐标分别表示股指期货和上证指数的对数收益率,横坐标表示时间样本数,每5 min取一个样本值.从图1可见当股指期货的收益率上涨或下降时,上证指数的收益率也上涨或下降,两个极小值收益率序列的波动趋于一致,这说明股指期货市场与股票市场之间的极小值收益率具有高度相依性.计算得股指期货和上证指数的极小值收益率序列的统计量见表1. 表1 极小值收益率序列的统计量 由表1可知SZX收益率序列、GZX收益率序列的J-B统计量均不服从正态分布.因为偏度值都大于零,所以都出现了右偏. 2.3 检验Clayton Copula函数 虽然参数θ的估计值在定义域内,但Clayton Copula函数是否能用来描述GZX与SZX收益率序列之间的相依性还需进一步检验.这里使用均匀分布的Q-Q图进行检验,结果见图2. 从图2中发现Q-Q图大致呈一条直线,即Clayton Copula函数能够高效准确地反映最小值收益率序列的相依性. 图2 收益率的Clayton Copula Q-Q图检验 图3 GZX与SZX对应收益率序列最优经验分布散点图 2.4 尾部相依性 2.4.1 最优经验分布散点图 用收益率序列的最优经验分布所得0-1序列的散点图(见图3),来研究对应极小值的尾部相依性.从图3可以看出,GZX与SZX对应收益率序列最优经验分布散点图具有很强的尾部相依性. 2.4.2 GZX与SZX收益率的相依性研究 由Clayton Copula函数计算下尾部相关系数:当α=0.925时,λL=0.802 9;当α=0.975时,λL=0.928 0;当α=0.995时,λL=0.985 0;当α→1时,λL= 0.591 6. 当GZX收益率超过q0.925,q0.975,q0.995时,SZX收益率超过对应分位数的概率分别为0.802 9,0.928 0,0.985 0,分别大于0.075,0.025,0.005,由此得出GZX与SZX收益率序列有较强的下尾部相依性.通过研究下尾部相依性,可知当GZX收益率暴跌时,SZX收益率发生大幅度下跌的概率是很大的. 通过实证研究,发现Clayton Copula函数能够较好地描述GZX与SZX收益率序列的下尾部相依性.即GZX收益率暴跌时,SZX收益率也暴跌的概率比较大,但上涨时相依性较弱.此结论与熊市期间我国股指期货与上证指数之间的实际走势基本一致.从熊市投资者投资行为上分析,投资者看到股指期货指数暴跌时,大多数投资者处于悲观氛围中,卖出股票,从而使得上证指数也随之暴跌;而股指期货指数暴涨时,大多数投资者的谨慎买入导致上证指数不会暴涨,或暴涨滞后.[8-9] [1] GUMBEL E J.Bivariate exponential distributions [J].Journal of American Statistical Association,1960,55:698-707. [2] CLAYTON D G.A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence [J].Biometrika,1978,65:141-151. [3] EMBRECHTS P,LINDSKOG F,MCNEIL A.Modeling dependence with Copulas and applications to risk management [M].Switzerland:Zürich,2001:55-58. [4] FREES E W,VALDEZ E A.Understanding relationships using Copulas[J].North American Actuarial Journal,1998,2(l):31-55. [5] GENEST C,RIVEST L P.Statistical inference procedures for bivariate archimedean Copulas [J].Journal of the American Statistical Association,1993,88:1034-1043. [6] HURLIMANN W.Fitting bivariate cumulative returns with Copulas [J].Computational Statistics & Data Analysis,2004,45:355-372. [7] ROCH O.Testing the bivariate distribution of daily equity returns using copulas.:an application to the Spanish stock markert[J].Computational Statistics & Data Analysis,2006,51:1312-1329. [8] 郑东.附加交易费用的动态投资组合鲁棒策略[J].东北师大学报(自然科学版),2014,46(6):30-34. [9] 霍俊爽.基于Gumbel Copula函数的金融高频数据极大值相依性[J].东北师大学报(自然科学版),2015,47(4):49-52. (责任编辑:李亚军) Extremeinterdependencyofthehigh-frequencydatainfinancialmarketsresearchbasedonClaytonCopulafunction HUO Jun-shuang1,ZHANG Ruo-dong1,PAN Shu-xia1,TAI Zhi-yan1,DONG Xiao-gang2 (1.Department of Mathematics,Jilin Medical College,Jilin 132013,China; 2.School of Basic Sciences,Changchun University of Technology,Changchun 130012,China) Based on Clayton Copula function,the dependency of the sequence yielded by 5 minutes minimum of index futures IF1112 index and SSE 000 001 is studied,and the interdependence of their microstructure is explored deeply. Copula function;Clayton Copula function;dependency 1000-1832(2017)03-0038-04 10.16163/j.cnki.22-1123/n.2017.03.009 2016-03-27 国家自然科学基金资助项目(11071026);吉林省教育厅“十二五”科学技术研究项目(2015393). 霍俊爽(1982—),男,硕士,副教授,主要从事应用统计研究. O 212.1 [学科代码] 110·2110 A2 实证分析

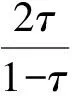
3 结论

