三角形的性质在圆锥曲线中的应用

魏怡，王运行

甘肃省兰州新区舟曲中学

三角形的性质在圆锥曲线中的应用

魏怡，王运行

甘肃省兰州新区舟曲中学

圆锥曲线一直是高考的热点，也是学生学习的难点，也是高中教学中的难点。圆锥曲线的难点就在于它可以与很多几何图形产生联系，比如三角形，这也是高频考点。如果学生能够在学习中熟练运用这些技巧，一定会起到事半功倍的作用。

圆锥曲线；三角形

在全国二卷的选择填空中，圆锥曲线经常出现在最后两道题，以压轴题的形式出现。在选择题中对圆锥曲线进行考察时，对技巧这一部分考查的比较多，笔者就涉及圆锥曲线的选择题进行了大量的比对，发现这一部分知识总是会与三角形的性质交融在一起进行考查。如果教师能够在教学的过程中将这些技巧进行总结，将会提升学生在这类题目上的正确率。下面笔者总结了几例三角形的性质与圆锥曲线交融的常考题型。

一、三角函数在圆锥曲线中的应用

-----→

例---1→：若以F为焦点的抛物线y2=4x上的两点A，B满足则弦AB的中点到准线的距离为？

分析：过A，B分别做准线l的垂线并与准线分别相交于A’，B’点，过B点作AA’的垂线，垂足为C。

假设BF=m,则AF=2m,利用抛物线的定义可知，BB’=C A‘=m,可得AC=m,BC=2 2m

总结：焦点弦问题是抛物线中的常考题型，如果能---够--→利用---已→知条件构造三角形，将会简化这类问题。该题中已知AF=2FB，利用准线构造直角三角形，∠BAC的正切就是焦点弦所在直线的斜率，避免了联立方程组所-----产→生的---复→杂运算。因此，在抛物线中遇到焦点弦问题，并且已知AF=mFB，都可用上述几何方法求得焦点弦所在直线的斜率。

例2：已知F1,F2为双曲线点，点P为双曲线C右支上一点，直线PF1与圆x2+y2=a2相切，且

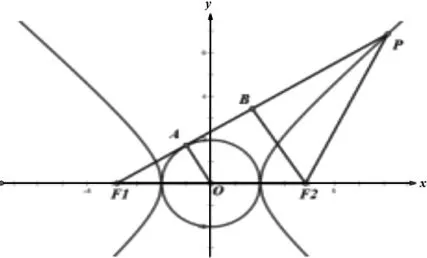
分析：如上图所示，设直线PF1与圆的切点为点A，过F2做PF1的垂线，垂足为B，由题意可知，ΔOAF1与ΔF2BF1均为直角三角形。

总结：离心率问题是圆锥曲线中的又一种常考题型，只要通过题目条件构造出有关a、b、c三者之间的关系式就可求得离心率。在该题中利用直角三角形的余弦公式作为桥梁，构造出等式，求出离心率，将复杂问题简单化。

二、“两边之和大于第三边，两边之差小于第三边”在圆锥曲线中的应用

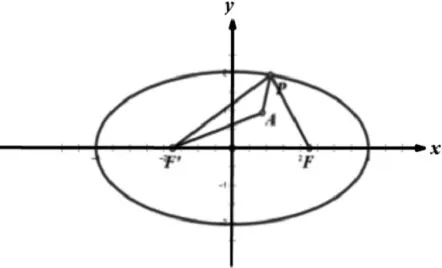
由此可得|PA|+|PF|=|PA|+（4-|PF'|）=4+（|PA|-|PF'|）

当P、A、F'三点共线，且P在AF'延长线上时，|PA|-|PF'|取得最大值。

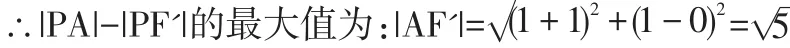
总结：此类问题属于椭圆定义的常考题，考点是椭圆的第一定义和第二定义，无外乎这两种考法，通过转化的方式都可以将问题转化为了一动点到一定点和到一定直线（定点）的距离最值问题，再利用三角形“两边之和大于第三边，两边之差小于第三边”的性质将问题解决。

三、“相似比”在圆锥曲线中的应用

例4：设抛物线y2=8x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C,其中点A，B在抛物线上（点A在第一象限），点C在y轴负半轴上，则ΔBCF与ΔABF的面积之比是分析：设椭圆的左焦点为F'，连接PF'、AF'.

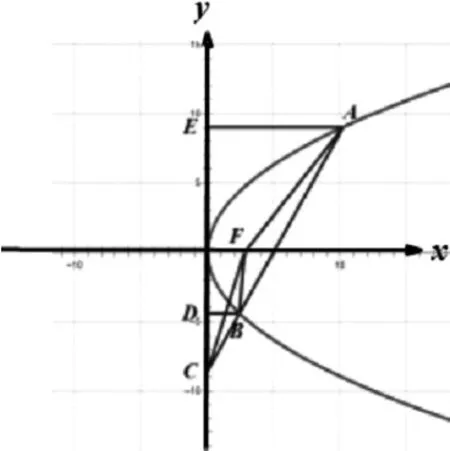
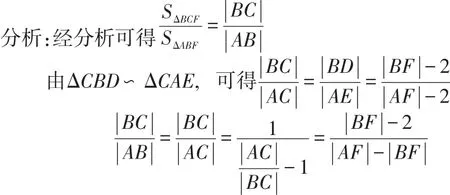
总结：该题中对抛物线的定义与三角形的相似原理进行了考查，利用相似比将问题转化为定义问题，将复杂问题简单化。

三角形是我们初中学习过的平面图形，是我们较为熟悉的一部分知识，进入高中后我们又学习了正余弦定理，在初中的基础上对三角形的性质进行了拓展。而圆锥曲线却是学生学习的难点，但是学生如果能将三角形与圆锥曲线联系起来，利用三角行的知识解决圆锥曲线的问题，能够达到化繁为简的效果，充分体现了高中数学中“复杂问题简单化”的思想。当然在圆锥曲线的题目中，有很多的题目是非常复杂的，需要我们利用其它几何图形所具有的性质，这就需要教师引导学生勤于思考，善于发现。