求同存异巧解化学题

王亚会

唐山市海港经济开发区第二中学

求同存异巧解化学题

王亚会

唐山市海港经济开发区第二中学

在解决化学问题时，充分运用求同存异的思想，深入地挖掘题目的共性和不同，并将两者有效的结合，能够极大地提高解题的速度，达到事半功倍的效果。

求同存异；氨基酸

求同存异，顾名思义就是寻求相同点，保留不同意见。在化学解题中，通过对问题条件的认真观察，充分挖掘物质之间的相同点和不同之处，挖掘内在规律，将无规律变成有规律，能够极大的简化运算过程，从而达到快速解题的目的。下面以多肽水解生成氨基酸为例，谈一下求同存异思想在化学解题中的应用。

下面是一个四肽，它可以看做是4个氨基酸缩合掉3个水分子而得。

式中R、R1、R2、R3可能是相同或不同的烃基，或有取代基的烃N10O19，已知它彻底水解后只得到下列四种氨基酸：

（1）这个多肽是几肽？（2）该多肽水解后，有几个谷氨酸？（3）该多肽水解后，有几个苯丙氨酸？

分析：（1）已知多肽由几个氨基酸脱水缩合而成，它就是几肽。通过观察可知，形成该多肽的四种氨基酸分子的共同特点是每个氨基酸中都有一个氨基，所以氨基的数目等于氨基酸的数目，因此该多肽为十肽。

（2）十个氨基酸分子脱去9个水形成分子式为C55H70N10O19的十肽，则10个氨基酸分子C、H、O、N总数为C55H70N10O19+9H2O= C55H88N10O28。通过观察，四种氨基酸的不同之处在于除谷氨酸每个分子中含有四个“O”外，其余的氨基酸分子中均含有两个“O”。

方法I：设谷氨酸分子有x个，其余氨基酸分子数目为y个。列二元一次方程如下：

由①②反应方程式解得x=4，y=6，即谷氨酸的数目为4个，其余氨基酸数目为6个。

方法II：如果每个氨基酸分子中都含有两个“O”，则10个氨基酸中“O”总数为20个，实际上“O”总数为28个，共多出来8个“O”，结合谷氨酸分子的结构特点，每个谷氨酸中含有4个“O”，即每个谷氨酸比其他氨基酸多两个“O”，所以谷氨酸分子总数为8÷2=4个。

（3）4个谷氨酸分子C、H、O、N总数为C20H36N4O16，10个氨基酸分子C、H、O、N总数为C55H88N10O28，则其余三种氨基酸C、H、O、N总数为C35H52N6O12。

方法I：已知甘氨酸的分子式为C2H5NO2，丙氨酸分子式为C3H7NO2，苯丙氨酸分子式为C9H11NO2,设甘氨酸有a个，丙氨酸有b个，苯丙氨酸为c个，建立方程组如下：

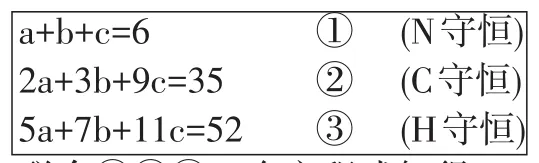
a + b + c = 6①( N守恒) 2 a + 3 b + 9 c = 3 5②( C守恒) 5 a + 7 b + 1 1 c = 5 2③( H守恒)

联合①②③三个方程式解得a=1，b=2，c=3。即苯丙氨酸的数目为3个。

方法II：

求同：甘氨酸、丙氨酸、苯丙氨酸三种氨基酸分子中均含有一个羧基，一个羧基产生的不饱和度“Ω”=1。

存异：甘氨酸、丙氨酸除羧基外，无其他不饱和结构，Ω=1，苯丙氨酸除含有一个羧基外，还含有一个苯环，Ω=5。笔者设想通过不饱和度的差异来求解苯丙氨酸的数目。已知35个C原子，按照饱和结构计算含有氢原子总数为（35×2+2）+6+5×2=88个(解释：“35×2+2”含义为“C”为饱和结构时，n个C对应“2n+2”个H；“+6”含义为每引入一个-NH2，相当于是一个“H”被一个“-NH2”替代，则有几个“-NH2”，氢原子个数就多几，所以有6个“-NH2”对应多6个“H”；比较难理解的是“5×2”的含义，举一个简单的例子，n个CH4对应氢原子个数为4n个，含有n个碳的饱和烷烃含有的氢原子数为2n+2个，即将n个饱和结构的分子连在一起“H”共减少4n-(2n+2)=2(n-1)个，所以6个饱和结构的分子连在一起个氢原子数减少了5×2=10个。我们总结一个公式，对于C原子数为n、N原子数为x的m肽分子，m个氨基酸分别按饱和结构计算对应“H”数为2n+2+x+2(m-1)个)。就本体而言，甘氨酸、丙氨酸、苯丙氨酸三种分子C、H、O、N总数为C35H52N6O12，即H原子数为52个，6个饱和分子中H原子数为88个，即H原子共减少了36个，即18个Ω。由6个氨基酸中的羧基产生的Ω=6，则由苯环产生的Ω=18-6=12，每个苯环有4个Ω，则苯环数目为3个，即共有3个苯丙氨酸。

为验证上面推论的准确性，我们来快速求解类似的问题。

蛋白质是由氨基酸组成的，一定条件下蛋白质或多肽可以水解，最终产物为氨基酸。今有1个多肽，其化学式为C32H44N6O7，已知它在一定条件下彻底水解只得到下列三种氨基酸：的物质的量为多少？

观察分析可知，每个氨基酸分子中均含有一个氨基和羧基，氮原子的数目等于氨基酸的数目，该多肽为六肽，形成六肽的6个氨基酸中C、H、O、N总数为C32H44N6O7+5H2O=C32H54N6O12，除所求化合物Ω为5个以外，其他均为1个（即由羧基产生的Ω），已知羧基共产生6个Ω，由上题推论可知Ω总数=（322+2+6+52-54）2=14，所以由苯环产生的Ω为14-6=8，故含两个苯环，因此1mol该多肽

可见，深入挖掘题目的共性和不同，利用求同存异的思想确实能优化运算过程，提高解题速度和效率。

[1]王祖浩.有机化学基础[M].江苏：凤凰出版传媒集团江苏教育出版社，2014：102-103.

[2]王秀平.化学计算中的“求同存异”[J].中国科教创新导刊, 2008,12：86.