求解PageRank问题的Arnold i-P IO算法

顾传青,聂影,王金波

(1.上海大学理学院,上海200444;2.保密通信重点实验室,成都610041)

求解PageRank问题的Arnold i-P IO算法

顾传青1,聂影1,王金波2

(1.上海大学理学院,上海200444;2.保密通信重点实验室,成都610041)

PageRank算法能帮助用户快速、准确地在巨量杂乱无章的信息中检索出有用的信息.两步分裂迭代法是用幂法来修正内外分裂(power-inner-outer,PIO)迭代法以加速PageRank算法.基于两步分裂迭代法,将预处理思想运用于求解PageRank问题,提出了求解Page-Rank问题的深度重启的Arnoldi算法加速的两步分裂迭代法,然后对此算法的收敛性进行了证明.数值实验结果证明,该算法的计算速度要快于两步分裂迭代法.

内外迭代法;两步分裂迭代法;深度重启的Arnoldi算法

网络是人们获取信息的重要来源,如何快速准确地从互联网上检索出需要的信息已成为判断搜索引擎优劣的重要指标.搜索引擎最核心的部分是搜索算法的设计.PageRank算法是用于网页排序的算法,是当今网络搜索引擎Google的核心技术.Google矩阵A定义如下:

式中,α∈(0,1)为阻尼因子,矩阵P由网络的超链接结构所定义,E=veT,e=(1,1,···,1)T∈Rn,其中v=e/n,n为矩阵A的维数.PageRank算法就是求解矩阵A对应的特征向量,即线性系统

幂法[1]是研究PageRank问题最经典的算法,但也存在线性收敛速度慢的不足.于是一些迭代算法被提出来解决这个问题.G leich等[2]提出利用内外迭代法求解PageRank问题.Gu等[3]提出了将幂法与内外迭代法结合的两步迭代法.Wu等[4]提出用重启的Arnoldi算法来修正幂法.

1 两步分裂迭代法和深度重启的Arnold i算法

1.1 内外迭代法

给定∥x∥=1(∥x∥为向量x的二范数)的初始向量,而x=Ax=(αP+(1-α)veT)x,则PageRank问题可以转化为求线性方程

的解.因为eTx=1,G leich等[2]引入参数β,把式(3)变成

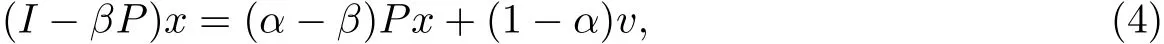
并用如下不动点迭代求解:

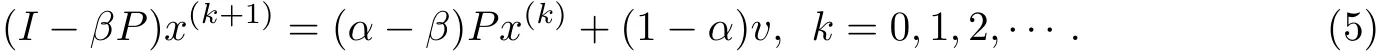
用Richardson迭代计算x(k+1),

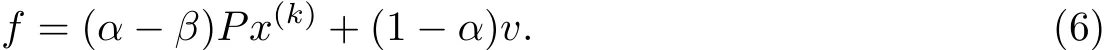
定义内线性系统(I-βP)y=f,应用Richardson内迭代可得

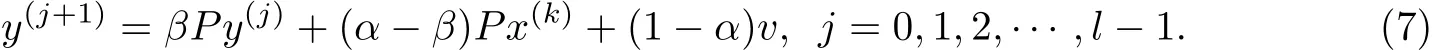
1.2 两步分裂迭代法

在内外迭代法的基础上,Gu等[3]提出了运用两步分裂迭代法求解PageRank问题,具体格式如下:给定一个初值x(0),计算

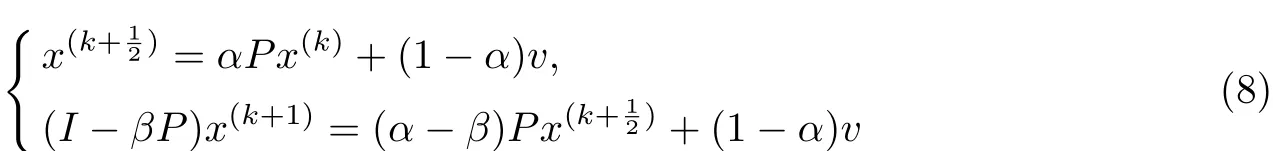
到序列{x(k)}.

1.3 深度重启的Arno ld i算法

深度重启的Arnoldi算法[4-5]可选择不同的初始向量,收敛到不同的特征值,具有更大的灵活性,算法过程如下.

步骤1给定K rylov子空间维数m,所需求的特征对的个数p≤m,控制精度tol和单位初始向量v1.

步骤2运行m步关于A和v1的Arnoldi过程,得到Vm+1,~Hm,Hm.计算Hm的所有特征对(~λi,yi),i=1,2,···,m.将Hm的特征值按模数递减排序,从中选出前p个最大的特征对,转向步骤5.

步骤3以vp+1为初始向量运行m-p步Arnoldi过程,得到Vm+1,,Hm.计算Hm的所有特征对,i=1,2,···,m.将Hm的特征值按模数递减排序,选择前p个特征对.

步骤4检验收敛性.对于得到的最大的Ritz值λ1和Ritz向量y1计算其残量.若满足计算精度,则选取~x1=Vmy1作为PageRank向量的近似解,算法停止,否则继续.

步骤5将选出的p个特征向量yi,i=1,2,···,p,正交化为2范数的单位向量.如果特征向量yi是复向量,需要实部和虚部分开存取,构造m×p阶矩阵Wp=[w1,w2,···,wp].如果有必要,可调整p的大小(比如使p增加或减少1).

步骤6通过在Wp的底部增加一行0形成(m+1)×p的矩阵=[Wp;0].令Wp+1= [~Wp,em+1],em+1是(m+1)×(m+1)阶单位矩阵Im+1的最后一列.显然(m+1)×(p+1)的矩阵Wp+1是正交矩阵.

步骤7使用步骤2得到的Vm+1和形成新的Vm+1和.返回步骤3.

2 求解PageRank问题的预处理两步分裂迭代法

本工作结合两步分裂迭代法和深度重启的Arnoldi算法,提出求解PageRank问题的深度Arnoldi重启的两步分裂迭代法.本算法的基本思想如下:给定一个初始向量,利用深度重启的Arnoldi算法得到一个粗糙的解;如果所求解还是没有达到收敛精度,则将深度重启的Arnoldi算法求得的解向量作为两步分裂迭代法的初始向量,利用两步分裂迭代法继续求解;重复上述过程,直到达到收敛精度.在此算法中,本工作利用参数α1,α2,restart和maxit控制两步分裂迭代法和深度重启的Arnoldi算法的转换.定义ratio=rcurr/rpre,ratio1=dcurr/dpre,利用ratio和ratio1保证算法的稳定性.选择α1=α-0.1或α-0.2,α2=α-0.1或α-0.2,提出以下Arnoldi-内外(Arnoldi-power-inner-outer,Arnoldi-PIO)迭代法.

(1)开始.给定初始向量v,选取K rylov子空间的维数m=8,期望的特征向量数p=4,参数α,β1和β2.参数α1,maxit用来控制两步分裂迭代法的重启数,restart=0,外迭代的误差r=1.

(2)运行深度重启的Arnoldi(2～3次).若是第1次,则运行1.3节中的步骤2～步骤7,否则运行步骤3～步骤7.如果残差范数满足收敛精度,算法停止,否则继续.

(3)由深度重启的Arnoldi算法得到的PageRank向量的近似解~x1作为两步分裂迭代法的初始向量.

restart=0;

while restartτ

x=x/∥x∥1;z=Px;

r=∥αz+(1-α)v-x∥2;

r0=r;r1=r;ratio=0;

while ratio<α1&r>τ

x=αz+(1-α)v;

z=Px;

f=(α-β)z+(1-α)v;

ratio1=0;

while ratio1<α2&d>η

x=f+βz;

d=∥f+βz-x∥2;

ratio1=d/d0;

d0=d;

end

r=∥αz+(1-α)v-x∥2;

ratio=r/r0;

r0=r;

end

x=αz+(1-α)v;

x=x/∥x∥1;

if r/r1>α1

restart=restart+1;

end

end

如果r<τ,则算法停止,否则转向步骤2.

3 算法收敛性的证明

Gu[3]给出了两步分裂迭代法的收敛性证明.Morgan[6]和Sorensen等[7]已经对深度重启的Arnoldi算法的收敛性给出证明.本工作将对Arnoldi-PIO算法给出一定的理论分析,证明其收敛性.将通过深度重启的Arnoldi算法求得的PageRank向量v1作为两步分裂迭代法的初始向量.通过两步分裂迭代法得到的向量为=,其中k≥maxit, G=(I-βP)-1((α-β)PA+A-αP),ω为规范化因子,n为P的维数.将作为m步标准Arnoldi过程(即深度重启的Arnoldi算法的第一步迭代)的初始向量,形成新的K rylov子空间:

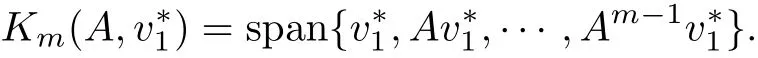
下面通过定理1可以证明上述过程的收敛性.

定理1假设矩阵A是可对角化矩阵,~Pm是Km(A,v∗1)上的正交投影,则

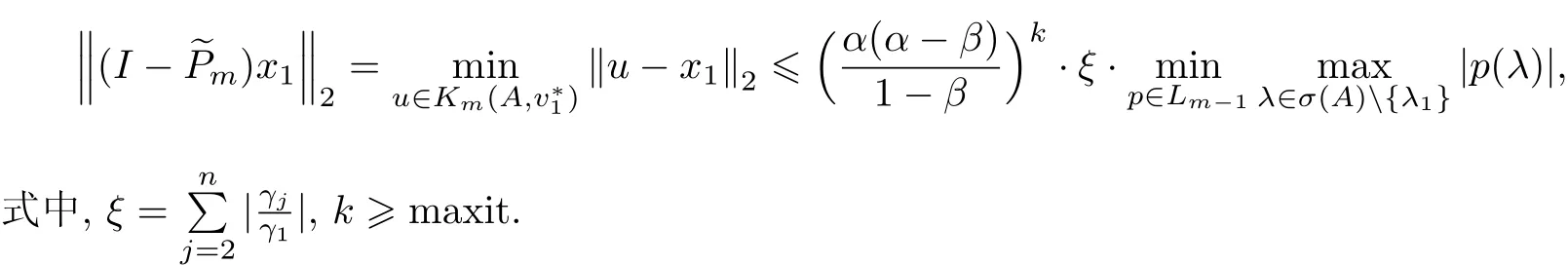
证明假设~Pm是Km上的正交投影,那么对任意的u∈Km,存在q(x)∈Lm-1使得

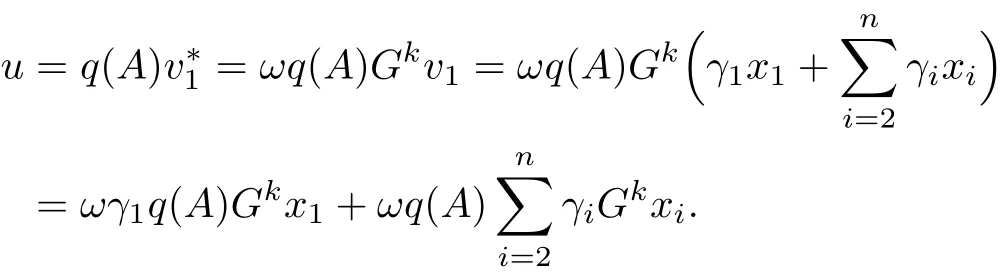
4 数值实验

本工作通过数值实验说明深度重启的两步分裂迭代法的有效性.所有的数值实验是在内存为4GB,主频为2.6 GHz,操作系统为W indows 8,处理器为Intel(R)Core(TM)i5-3230MCPU的计算机上使用MATLAB(R2014a)进行的.用tCPU表示运算时间,以s为单位,Mat-Vec表示矩阵向量积数.对于内外迭代法,选取适当的参数有利于体现算法的有效性.数值实验选取β=0.5和η=10-2.为了保证数值实验的公平性,在两步分裂迭代法和深度重启的两步分裂迭代法中同样取η=10-2.为了说明测试算法的相对加速效果,定义

4.1 数值算例1

算例1的测试矩阵Hollins包括6 012个网页和23 875个链接.本算例给出了内外(Innout)迭代法、两步分裂(PIO)迭代法和深度重启的两步分裂(Arnoldi-PIO)迭代法的计算时间与矩阵向量积数.表1给出了3种算法的数值结果,图1根据不同的α绘制了3种算法的收敛曲线.

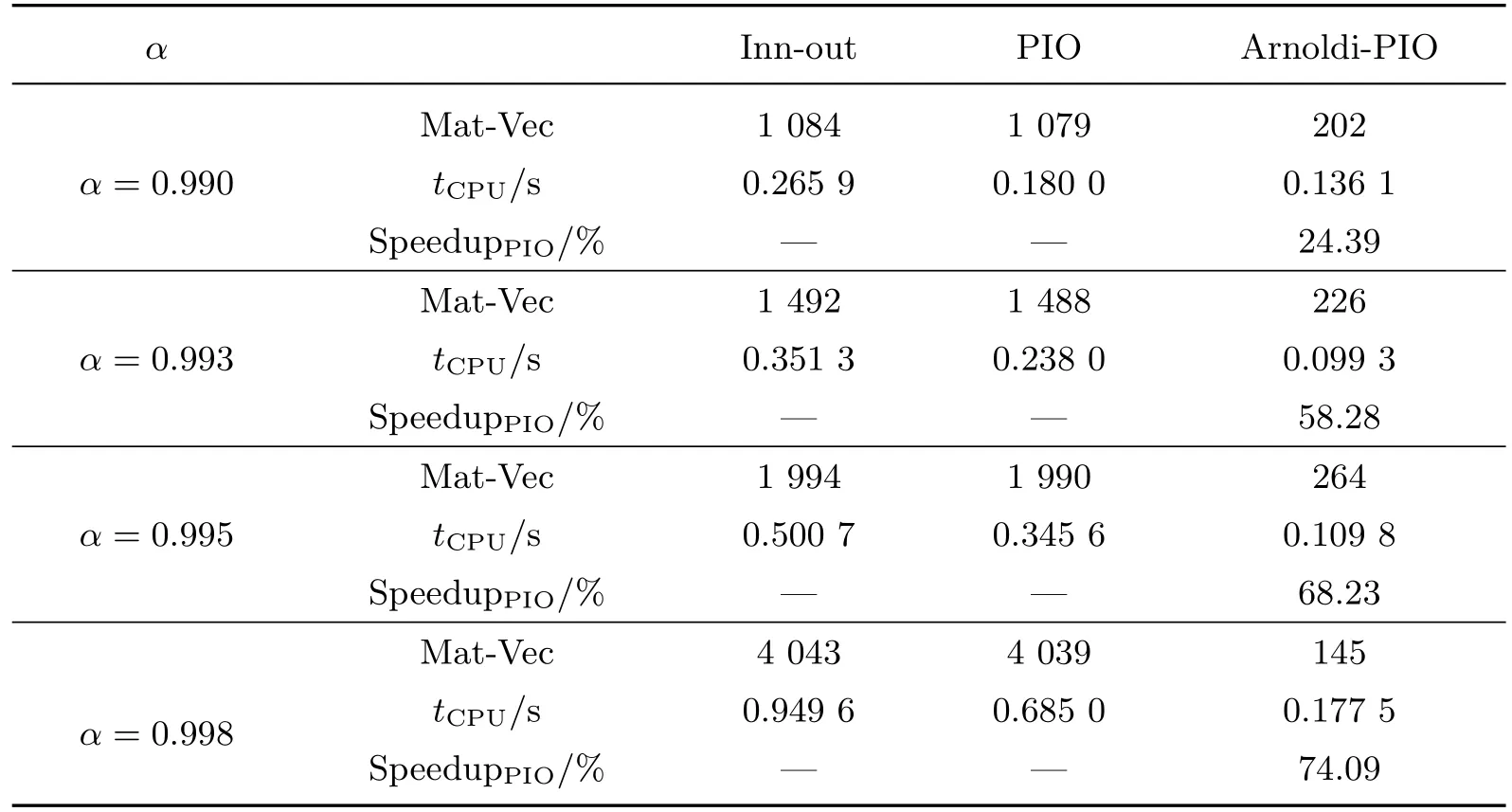
表1 关于Hollins矩阵3种算法的数值结果(τ=10-8)Tab le 1 Numerical resu lts of three algorithms for Hollinsmatrix(τ=10-8)

算例1的实验结果表明,Arnoldi-PIO算法性能相对于其他两种算法有显著的改善.对于矩阵Hollins,当α=0.998时,Arnoldi-PIO算法仅用0.177 5 s就达到了精度要求,PIO算法用了0.685 0 s、Inn-out用了0.949 6 s才达到精度要求.由图1中残量范数和迭代步数的关系可观察到,Arnoldi-PIO算法的收敛速度是最快的,由此可验证深度重启的两步分裂迭代法的有效性.

4.2 数值算例2

算例2选取的测试矩阵是Stanford-Berkeley,包含683 446个网页和7 583 376个链接.表2给出了Inn-out,PIO和Arnoldi-PIO 3种迭代算法的的数值结果.图2根据不同的α绘制了随着迭代步数的增加,残差范数的变化情况.

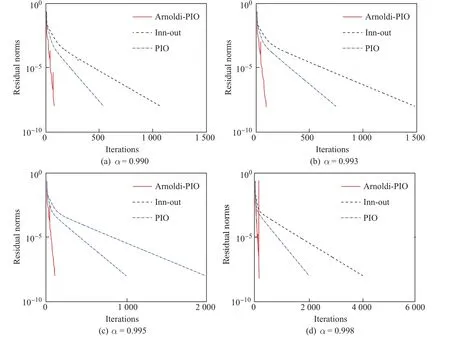
图1 关于Hollins矩阵3种算法的收敛性分析(τ=10-8)Fig.1 Convergence analysis of three algorithms for Hollinsmatrix(τ=10-8)

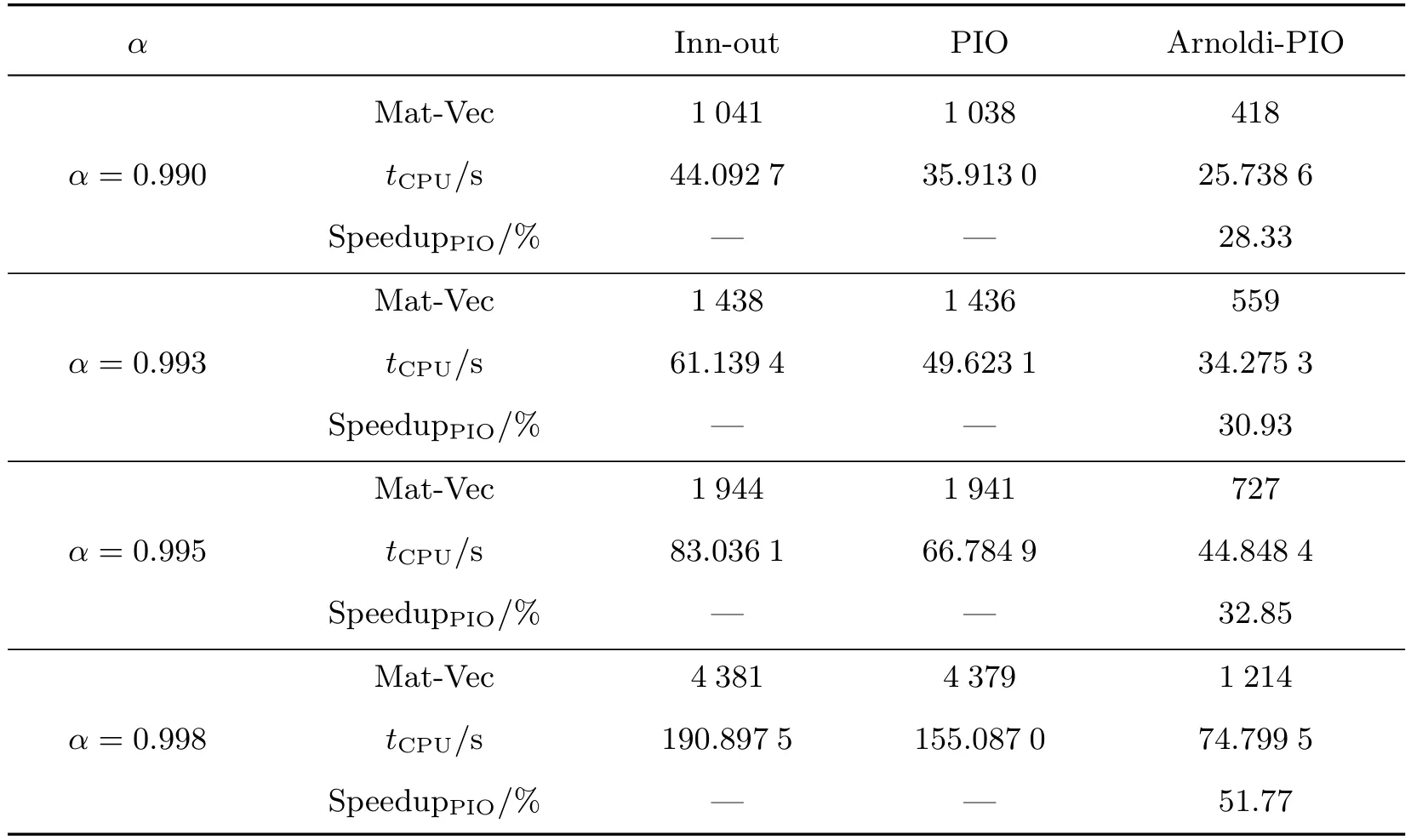
表2 关于Stan ford-Berkeley矩阵3种算法的数值结果(τ=10-8)Tab le 2 Numerical resu lts of three algorithms for Stanford-Berkeley matrix(τ=10-8)

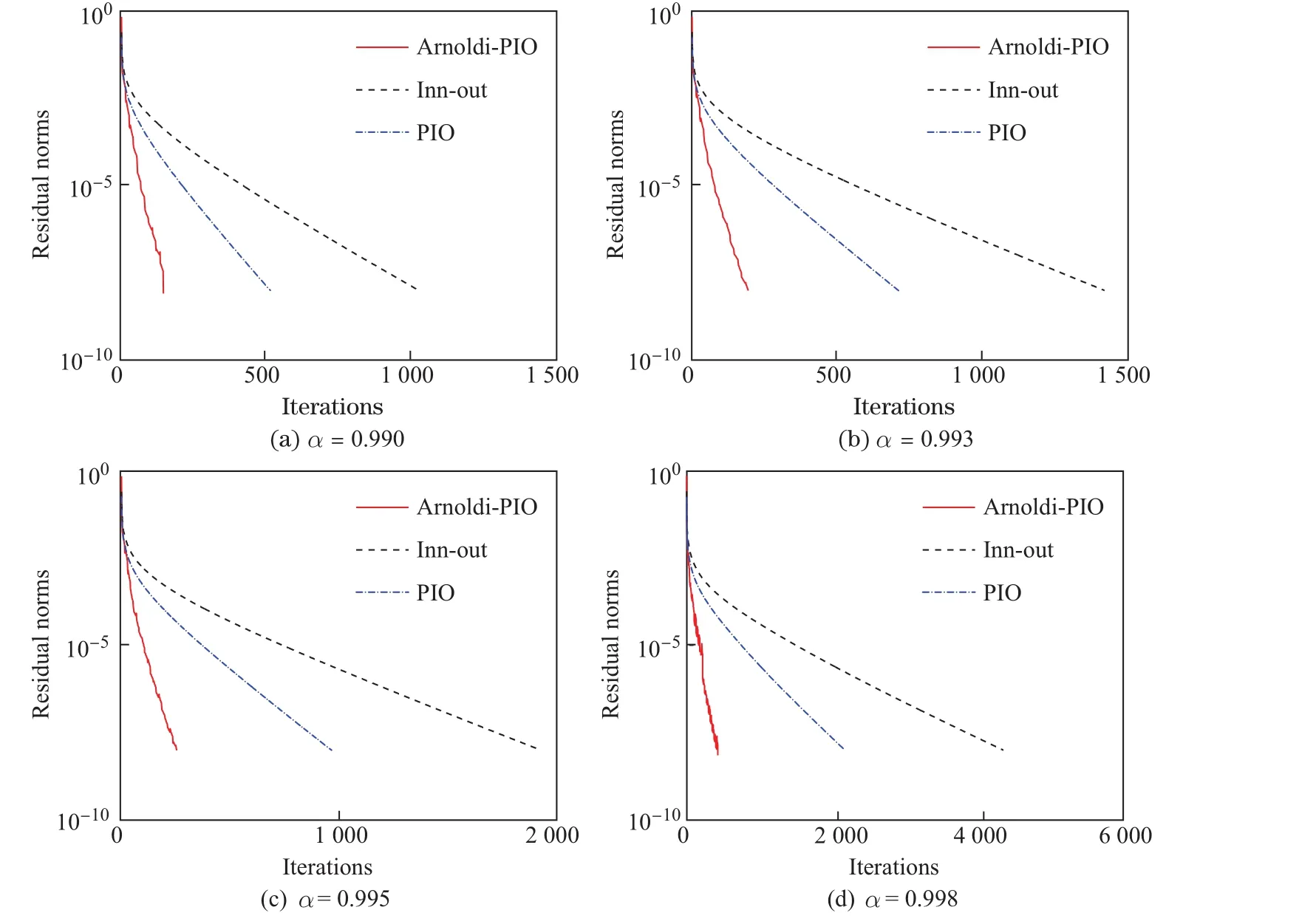
图2 关于Stanford-Berkeley矩阵3种算法的收敛性分析(τ=10-8)Fig.2 Convergence analysis of three algorithms for Stan ford-Berkeley matrix(τ=10-8)

由表2可知,Arnoldi-PIO算法相比另两种算法使用了更少的计算时间与矩阵向量积数,效果却最好.图2描述了当α=0.990,0.993,0.995,0.998时3种算法的迭代次数,可知Arnoldi-PIO算法的收敛速度是最快的.因此,Arnoldi-PIO算法的有效性得以验证.

[1]PAGE L,BRIN S,MOTWANI R,et al.The PageRank citation ranking:bring order to the web[R/OL].(2001-10-30)[2014-06-20].http://ilpubs.stan ford.edu:8090/422/1/1999-66.pd f.

[2]GLEICH D,GRAY A,GREIF C,et al.An inner-outer iteration method for computing PageRank[J].SIAMJ Sci Compute,2010,32(1):349-371.

[3]GU C Q,X IE F,ZHANG K.Atwo-stepsplitting iteration for computing PageRank[J].Journal of Computational and Applied Mathematics,2015,278:19-28.

[4]W U G,W EI Y M.APower-Arnoldi algorithmfor compuring PageRank[J].Numer Linear Algebra Appl,2007,14:521-546.

[5]W U K,SIMON H.Thick-restart Lanczosmethod for large symmetric eigenvalue problems[J]. SIAMJournal on Matrix Analysis and Applications,2000,22:602-616.

[6]MORGAN R.Aharmonic restarted Arnoldialgorithmfor calculating eigenvalues and determing multiplicity[J].Linear Algebra and Its Applications,2006,415:96-113.

[7]SORENSEN D.Implicit application of polynomial fi lters in a k-stepArnoldimethod[J].SIAMJournal on Matrix Analysis and Applications,1992,13:357-385.

Arnold i-PIO algorithmfor PageRank

GU Chuanqing1,NIE Ying1,WANG Jinbo2
(1.College of Sciences,Shanghai University,Shanghai 200444,China; 2.Science and Technology on Communication Security Laboratory,Chengdu 610041,China)

The PageRank algorithmplays an important role in determining the importance of Web pages.The power-inner-outer(PIO)method is a two-stepsplitting iteration framework that combines the inner-outer scheme with the classical power method to accelerate the computation of PageRank algorithm.This paper proposes an Arnoldi-PIO algorithm,which is a PIO iteration algorithmmodified with the thick restarted Arnoldi method.Description and convergence of the proposed algorithmare discussed in details. Numerical resu lts show effi ciency and convergence behaviors of the algorithm.

inner-outer iteration;two-stepsplitting iteration;thick restarted Arnoldi algorithm

O 212

A

1007-2861(2017)04-0555-08

DO I:10.12066/j.issn.1007-2861.1867

2016-10-13

国家自然科学基金资助项目(11371243);上海市重点学科建设资助项目(S30104);中国电子科技集团公司第三十研究所委托项目

顾传青(1955—),男,教授,博士生导师,研究方向为数值逼近、数值代数及其应用.

E-mail:cqgu@shu.edu.cn