纤维增强聚合物布加固黏弹性木梁弯曲的解析解
欧阳煜,江勇,周磊
(上海大学土木工程系,上海200444)
纤维增强聚合物布加固黏弹性木梁弯曲的解析解
欧阳煜,江勇,周磊
(上海大学土木工程系,上海200444)
将木梁视为服从标准线性固体本构的黏弹性体,假定纤维增强聚合物(fiber reinforced polymer,FRP)布与木梁紧密粘贴,研究了FRP布加固木梁线性弯曲的蠕变行为.在建立FRP布加固黏弹性矩形截面木梁弯曲变形控制方程的基础上,利用Laplace变换,给出了突加均布载荷作用下FRP布加固简支黏弹性木梁弯曲的解析解.根据相关试验数据,确定了花旗松(Douglas-fi r,DF)木梁标准线性固体本构的材料参数,分析了芳纶纤维增强塑料(aramid FRP,AFRP)布含量和梁跨高比等对AFRP布加固简支DF木梁弯曲变形的影响.结果表明: AFRP布加固可有效减小木梁的蠕变挠度;随着DF木梁蠕变的增加,AFRP布加固DF木梁的中性轴逐渐靠近粘贴AFRP布的侧边,且随着DF木梁跨高比或AFRP布含量的提高, AFRP布加固DF木梁的最大压应力和最大拉应力减小.
纤维增强聚合物;加固;木梁;黏弹性;解析解
木结构具有自重较轻、节能环保、施工方便等优点,被日本、欧洲和北美等国家和地区广泛使用,并且也是国内现存寺庙、塔楼等的主要结构形式.作为纤维性材料,木材具有明显的流变特征,使得木结构在使用中会产生明显的蠕变行为.同时,由于木材弹性模量和强度较低,且易腐蚀等,因此木结构及其构件需要定期地修复和加固[1-4].
已有研究表明,采用纤维增强聚合物(fiber reinforced polymer,FRP),如玻璃纤维(glass FRP,GFRP)、碳纤维(carbon FRP,CFRP)和芳纶纤维(aramid FRP,AFRP)等可有效修复和提高木构件的承载力,减小变形,并弥补木构件力学性能老化等缺陷[1].在木梁加固方面,已有学者对FRP材料提高木梁的抗弯[1-2,5-9]和抗剪性能[1,10-14]进行了广泛的实验研究、理论分析和有限元数值模拟.针对木梁的蠕变力学行为,Plevris等[15-16]研究了FRP加固木梁和钢筋混凝土梁的蠕变行为,而Davids等[17]研究了FRP加固层合木梁的蠕变变形,给出了木材的黏弹性本构关系,并提出了数值计算方法.Yahyaei-Moayyed等[18-19]和陆伟东等[20]采用黏性材料的Findley幂律模型研究了木材的蠕变性能,并研究了FRP对木梁的加固效果.Lu等[21]研究了不同试验环境和应力水平下FRP加固层合木梁的弯曲蠕变,而Pulngern等[22]采用Find ley幂律模型,利用Abaqus有限元软件研究了木-PVC组合构件的短期性能和长期蠕变行为.可见,已有的研究成果主要是基于Find ley幂律模型,通过试验或有限元数值仿真研究木梁的黏弹性行为,分析FRP的加固效果.
黏弹性材料的标准线性固体本构模型已得到了广泛应用.为此,本工作将木梁视为服从标准线性固体本构的黏弹性体,研究底部黏贴FRP布加固木梁弯曲的蠕变行为.基于木梁与FRP布紧密黏贴以及Euler-Bernoulli梁的弯曲变形假定,建立了FRP布加固黏弹性矩形木梁弯曲变形的控制方程,通过Laplace变换及其逆变换,给出了突加均布载荷作用下FRP布加固简支黏弹性木梁弯曲的解析解.在此基础上,利用已有的试验数据确定了南美黄松(southern yellow pine,SYP)和花旗松(Douglas-fi r,DF)木材标准线性固体本构的材料参数,并分析了AFRP布含量和梁跨高比等对AFRP布加固简支DF木梁弯曲变形蠕变行为的影响.
1 FRP布加固黏弹性矩形木梁弯曲的控制方程
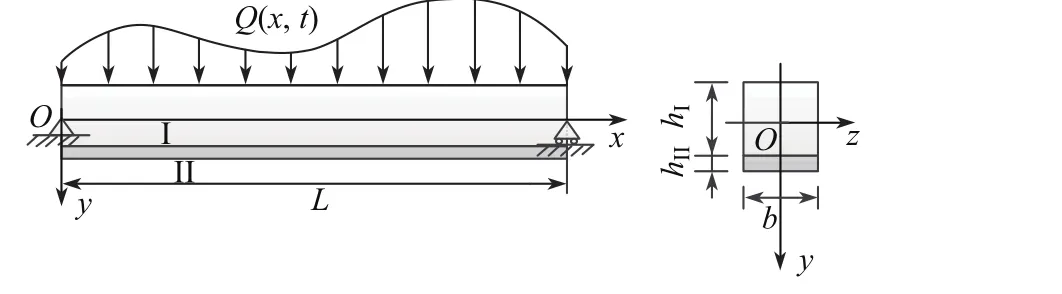
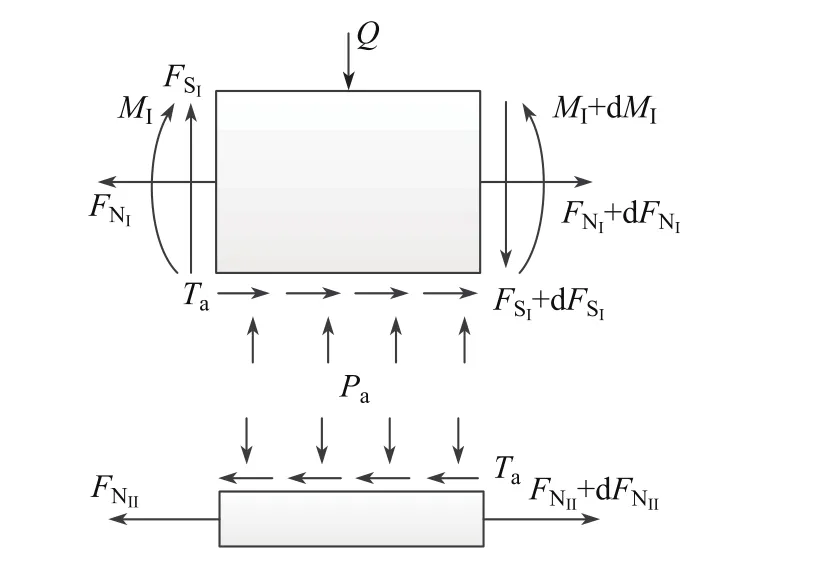
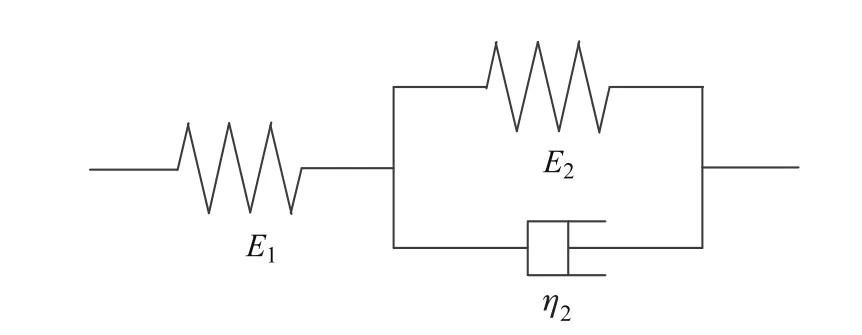
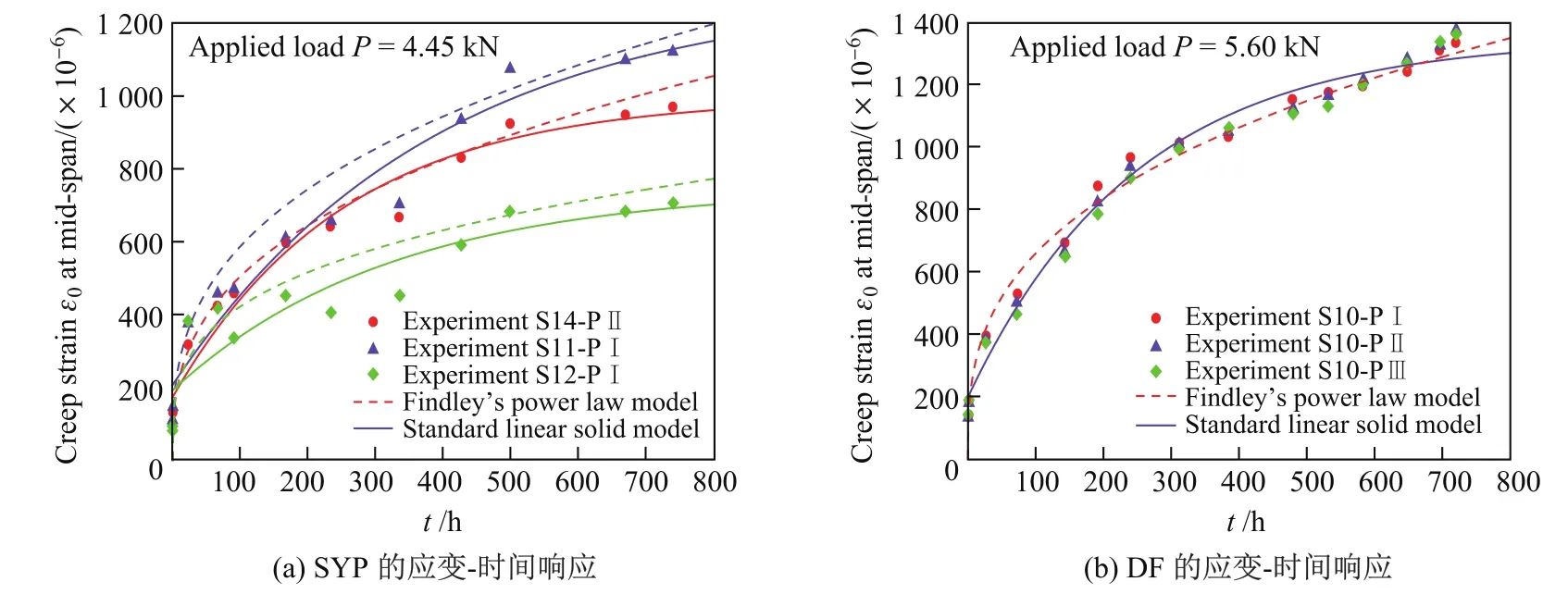
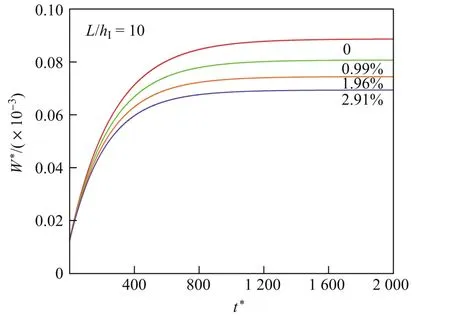
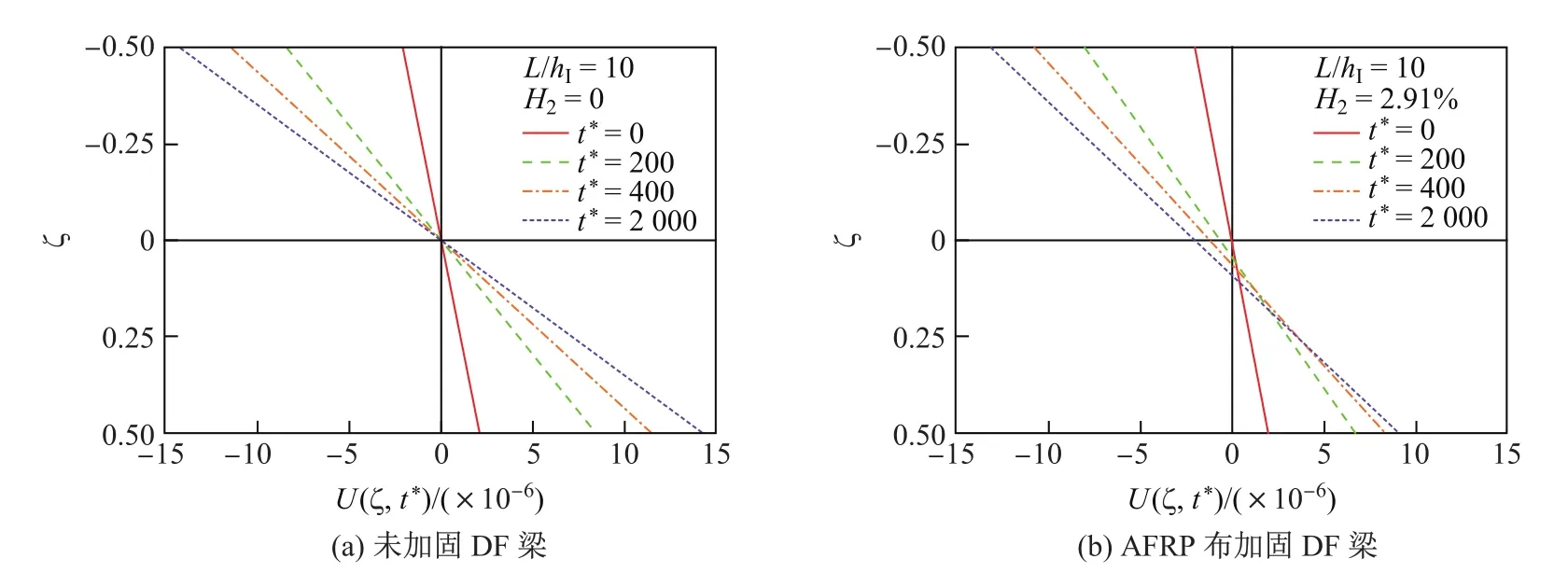
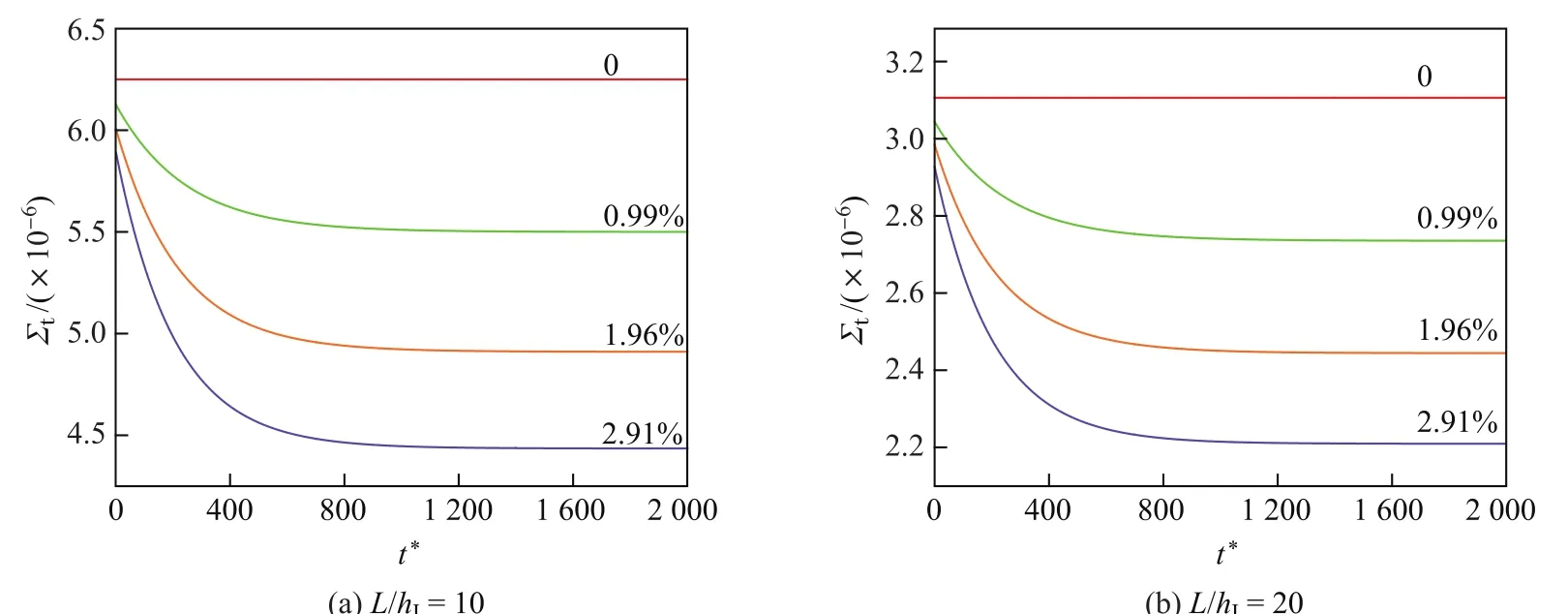
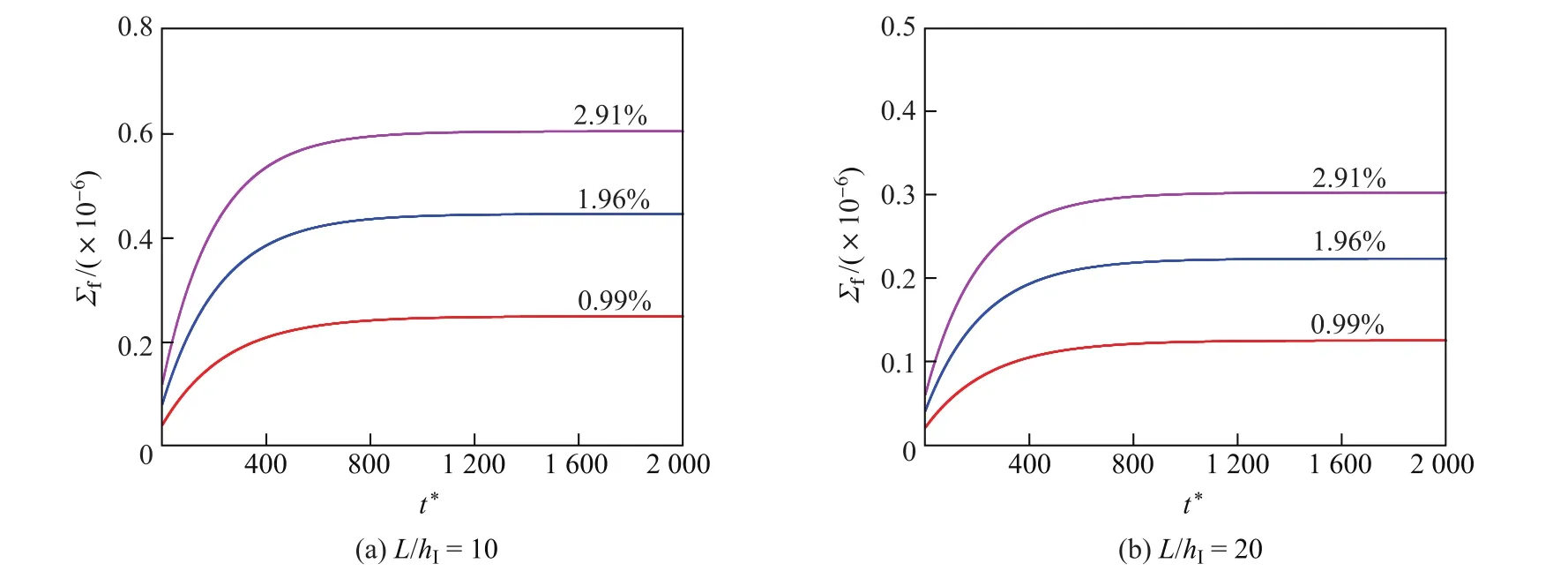
如图1所示,设长为L、宽为b、高为hI的矩形截面木梁下部贴有FRP布,且承受横向载荷Q(x,t)的作用,木梁的松弛模量为Y(t),横截面面积和形心主惯轴的惯性矩分别为AI和II,且形心到木梁底部的距离为rI;FRP布的弹性模量为EII,宽和厚分别b和hII(hII 以木梁轴线为Ox轴,建立直角坐标系Oxyz,并记木梁轴线上点的轴向位移为u(x,t),横向挠度为w(x,t),则根据变形假定,木梁任一点(x,y,z)的轴向位移、横向位移和轴向应变可分别表示为 图1 FRP布加固木梁的几何尺寸F ig.1 Geometric parameters of timber beamstrengthened by FRP sheet FRP布的轴向位移和轴向应变可分别表为 采用黏弹性材料的积分松弛型本构方程[23],则木梁和FRP布的轴向应力分别为 FRP布横截面上的轴力FNII为 将FRP布等效为薄膜,记木梁横截面上的剪力为FSI,木梁与FRP布之间的轴向和横向作用力分别为Ta和Pa,则由图2单元体d x平衡可得 图2 FRP布加固木梁单元体d xF ig.2 Element d x of timber beamstrengthened by FRP sheet 由式(11)中第一个方程可得 将其代入式(10)中的第一个方程得 由式(10)中第二个方程和式(11)中第一个方程可得 假定FRP布加固木梁无净轴力,即FN=FNI+FNII=0,则有 将式(9)代入式(6)中的第三个方程,可得 方程式(15)和(16)构成FRP布加固黏弹性木梁弯曲的基本控制方程.由上述推导可见,对于其他截面形式的FRP加固木梁,只要将截面几何参数进行相应的替换,控制方程式(15)和(16)仍成立. 假定初始时FRP布加固黏弹性木梁未变形,则FRP布加固简支黏弹性木梁弯曲的初边值问题为 通过Laplace逆变换,由式(26)和(28)可得FRP布加固简支黏弹性木梁弯曲在时间域的u(x,t)和w(x,t)响应.然而,对于任意给定的载荷Q(x,t)和木梁松弛模量Y(t),通常情况下很难得到式(26)和(28)的Laplace逆变换解析解.这里假定木梁为服从标准线性固体本构的黏弹性体[23],即松弛模量Y(t)取为 服从标准线性固体本构的黏弹性体可视为如图3所示的黏弹性三参量本构模型,其中E1和E2分别为相应弹性元件的弹性模型,而η2为黏性元件的黏滞系数,且 式(29)的Laplace变换为 图3 黏弹性三参量本构模型Fig.3 Three-element creepmodel of viscoelasticity 对均布突加载荷Q(x,t)=Q0H(t),其中Q0为均布载荷的值,H(t)为Heaviside函数. Q(x,t)的Laplace变换为 此时,式(27)化为 而式(22)和(28)化为 对式(34)进行Laplace逆变换,可得 式中, 式中,T为单位时间,由于本工作黏滞系数单位取GPa/h,故取T=1 h.FRP布加固木梁轴线的无量纲挠度和水平位移可分别表示为 至此,得到了FRP布加固简支黏弹性木梁弯曲变形的解析解式(36)或(40). 进一步的分析表明:对于FRP布加固简支黏弹性木梁,只需将式(40)中的因子(ξ4-2ξ3+ ξ)和(2ξ3-3ξ2)分别替换为(ξ4-2ξ3+ξ2)和(2ξ3-3ξ2+ξ),便可得到FRP布加固简支黏弹性木梁的弯曲解析解. 3.1 木材的蠕变模型 Yahyaei-Moayyed等[19]研究了南美黄松(SYP)以及花旗松(DF)的蠕变行为.试件尺寸为38 mm×38 mm×500 mm.试验采用四点弯曲的加载方式,其中支座间距为432 mm,两突加集中载荷垂直作用于梁上,且距支座165 mm,间距为102 mm.假定温度和湿度保持不变,记录梁底应力、应变与时间的相关数据.根据Find ley幂律模型: 给出了材料参数m,k和n(见表1),然而这些参数的物理意义欠明确.本工作基于该试验结果,采用黏弹性体的标准线性固体模型刻画木材的黏性性质.黏弹性体标准线性固体本构的蠕变形式为 图4 木梁跨中最外层纤维的应变-时间响应Fig.4 Responses of themid-span strains of the outer most fibre vs.time 根据相关试验结果[19],利用最小二乘法可分别拟合SYP和DF材料标准线性固体模型的本构参数E1,E2和η2.图4分别给出了SYP和DF的试验数据及Find ley幂律模型和标准线性固体模型的拟合曲线,其中实线为标准线性固体本构模型式(39)的拟合结果,而虚线为Find ley幂律模型拟合结果.可见,两种蠕变模型均能很好地与试验数据吻合,并且对取自同一木料制成的DF试件的蠕变拟合呈现高度一致.表1给出了两种模型本构参数的拟合结果. 表1 SYP和DF木材的Find ley幂律模型和标准线性固体模型参数Tab le 1 Model parameters of Find ley’s power law and standard linear solid model of the SYP and DF woods 3.2 参数分析 由于现有的取自同一木料的试验数据很少,故选取各物理参数的平均值来分析FRP布加固木梁的蠕变响应.为重点考察FRP布加固对简支黏弹性木梁力学性能的影响,取Q∗=1×10-3,hI=b=0.1 m,并采用表1中DF材料参数的平均值,即E1=247.72 GPa,E2= 42.62 GPa,η2=11.60 GPa·h,以及文献[19]中AFRP布受荷500 h的弹性模量EII= 124GPa进行计算和分析.此时,无量纲材料参数为 加固木梁AFRP含量定义为H2=hII/h,即AFRP布加固木梁横截面中AFRP布的面积占加固木梁横截面总面积的百分数,由此可得无量纲几何参数H1=1-H2,γ3= (1-H2)/H2,γ4=3γ3. 图5给出了跨高比L/hI=10时,不同AFRP含量H2下AFRP布加固简支DF梁跨中无量纲挠度W∗=W(0.5,t∗)随无量纲时间t∗的响应.图6给出了不同无量纲时刻t∗时,未加固DF梁(H2=0)和含量H2=2.91%的AFRP布加固DF梁无量纲挠度W=W(ξ,t∗)沿梁轴线的分布,其中虚线和实线分别为未加固DF梁和AFRP布加固DF梁的挠度分布.可见,对给定跨高比L/hI,无量纲挠度W∗随无量纲时间t∗的增加而增大,并趋于稳定值,并且无量纲挠度W∗随AFRP布含量的增加而减小.当t∗=0时,H2分别为0.99%,1.96%和2.91%的AFRP布加固木梁的弹性挠度W∗分别比未加固木梁(即H2=0)降低1.46%,2.92%和4.22%;而当无量纲挠度W∗的蠕变达到稳定值,即t∗→∞时,AFRP布加固木梁挠度W∗分别比H2=0时降低9.00%,16.07%,21.78%,即AFRP加固可有效减小木梁的蠕变挠度.同时,从解析解(40)可以发现,无量纲挠度W∗的减小量不依赖于无量纲载荷Q∗、跨高比L/hI和梁宽b. 图5 不同AFRP布含量H2时,AFRP布加固DF梁无量纲跨中挠度W∗随无量纲时间t∗的响应Fig.5 Responses of non-dimensionalmid-span deflections W∗vs.non-dimensional time t∗of AFRP-reinforced DF beamfor volume fractions H2of AFRP 图6未加固DF梁与当H2=2.91%时,AFRP布加固DF梁无量纲挠度W(ξ,t∗)的分布Fig.6 Distributions of non-dimensional deflections W(ξ,t∗)of unreinforced and AFRP-rein forced DF beamwhen H2=2.91% 图7 给出了不同无量纲时刻t∗时,未加固DF梁和H2=2.91%的AFRP布加固DF梁端部ξ=1处横截面无量纲轴向位移U(ζ,t∗)=ut/L沿DF梁无量纲高度坐标ζ=y/h的分布.可见,随着无量纲时间t∗的增大,未加固DF梁和AFRP布加固DF梁的端部轴向位移(横截面转角)均逐渐增大,但对未加固DF梁,其中性轴位置不变,而对于AFRP布加固DF梁,其中性轴逐渐靠近粘贴AFRP布的侧边. 图7不同无量纲时刻t∗时,未加固DF梁和AFRP布加固DF梁端ξ=x处无量纲轴向位移U(ζ,t∗)沿无量纲高度ζ的分布Fig.7 Distributions of the non-dimensional axial displacements U(ζ,t∗)at endξ=x of the unreinforced and AFRP-reinforced DF beamalong the non-dimensional high coordinateζfor diff erent non-dimensional instant time t∗ 图8 和9分别给出了不同跨高比L/hI和AFRP含量H2下,AFRP布加固DF梁跨中无量纲最大压应力Σc=σI/E1|ζ=-rI,ξ=0.5和无量纲最大拉应力Σt=σI/E1|ζ=rI,ξ=0.5随无量纲时间t∗的响应.可见,对给定的跨高比L/hI,随着无量纲时间t∗的增加,AFRP布加固DF梁的无量纲最大压应力Σc和无量纲最大拉应力Σt的数值均逐渐减小,并趋于稳定值,拉应力Σt的变化幅度大于压应力Σc.同时,随着AFRP布加固DF梁跨高比L/hI或AFRP布含量H2的提高,DF梁的最大压应力Σc和最大拉应力Σt均减小.这是因为随着梁跨高比L/hI或AFRP布含量H2的提高,AFRP布承担的载荷增加,从而导致DF梁应力的减小. 图10分别给出了不同跨高比L/hI和AFRP布含量H2下,AFRP布加固DF梁跨中AFRP布无量纲拉应力Σf=σII/E1|ζ=rI,ξ=0.5随无量纲时间t∗的响应.可见,对给定的跨高比L/hI,随着无量纲时间t∗的增加,AFRP布的无量纲拉应力Σf增大,并趋于稳定值,并且随着AFRP布含量H2的提高和跨高比L/hI的减小,无量纲拉应力Σf增大. 本工作考虑了木梁的黏弹性性质,研究了FRP布加固木梁的线性弯曲行为.首先,在木梁材料服从标准线性固体本构和木梁与FRP布紧密粘贴的假定下,建立了FRP布加固黏弹性矩形木梁弯曲变形的控制方程,通过Laplace变换及其逆变换,给出了突加均布载荷作用下FRP布加固简支黏弹性木梁弯曲的解析解.然后,在此基础上,基于相关的试验数据,确定了南美黄松(SYP)和花旗松(DF)木材标准线性固体本构的材料参数,并分析了AFRP布含量和梁跨高比等对AFRP布加固DF梁弯曲变形蠕变行为的影响.最后,得到如下结论. (1)木材黏性对木梁的弯曲力学性能有显著的影响,AFRP布加固木梁不仅可减小木梁初始弹性挠度,而且可有效减小其蠕变挠度; (2)随着时间增加,未加固或AFRP布加固DF梁端部转角均逐渐增大,但对于AFRP布加固DF梁,其中性轴逐渐靠近粘贴AFRP布的侧边. (3)随着时间增加,AFRP布加固DF梁的最大压应力和最大拉应力均逐渐减小,并趋于稳定值,且随着DF梁跨高比或AFRP含量的提高,AFRP布加固DF梁的最大压应力和最大拉应力减小. (4)随着AFRP含量H2的提高和跨高比L/hI的减小,AFRP布拉应力Σf增大. 图8 不同跨高比L/hI和AFRP布含量H2下,AFRP布加固DF梁无量纲最大压应力Σc随无量纲时间t∗的响应Fig.8 Responses of non-dimensionalmaximumcompressive stressΣcof AFRP-reinforced DF beamvs.non-dimensional time t∗for diff erent span-depth ratio L/hIand volume fraction H2of AFRP 图9 不同跨高比L/hI和AFRP含量H2下,AFRP布加固DF梁无量纲最大拉应力Σt随无量纲时间t∗的响应Fig.9 Responses of non-dimensionalmaximumtensional stressΣtof AFRP-reinforced DF beamvs.non-dimensional time t∗for diff erent span-depth ratio L/hIand volume fraction H2of AFRP 图10 不同跨高比L/hI和AFRP含量H2下,AFRP布加固DF梁中AFRP布无量纲拉应力Σf随无量纲时间t∗的响应Fig.10 Responses of non-dimensional tensional stressΣfof AFRP sheet in AFRP-rein forced DF beamvs.non-dimensional time t∗for diff erent span-depth ratio L/hIand volume fraction H2of AFRP [1]RADFORD D W,GOETHEMD V,GUTKOWSKI R M,et al.Composites repair of timber structures[J].Construction and Building Materials,2002,16(7):417-425. [2]BORRI A,CORRADIM,GRAZINI A,et al.Amethod for flexural reinforcement of old wood beams with CFRP materials[J].Composites Part B:Engineering,2005,36(2):143-153. [3]庄荣忠,杨勇新.FRP加固木结构的研究和应用现状[J].四川建筑科学研究,2008,34(5):89-92. [4]DE JESUSAMP,PINTO JMT,MORAISJ J L,et al.Analysis of solid wood beams strengthened with CFRP laminates of distinct lengths[J].Construction and Building Materials,2012, 35(1):817-828. [5]杨会峰,刘伟庆,邵劲松,等.FRP加固木梁的受弯性能研究[J].建筑材料学报,2008,11(5):591-597. [6]VALIpOUR H R,CREWS K.Effi cient finite element modelling of timber beams strengthened with bonded fibre reinforced polymers[J].Construction and Building Materials,2011,25(12): 3291-3300. [7]卢欣,杨骁,宋少沪,等.纤维增强聚合物布加固木梁的非线性弯曲分析[J].上海大学学报(自然科学版),2012,18(6):634-639. [8]ALHAYEK H,SVECOVAD.Flexural stiff ness and strength of GFRP-reinforced timber beams[J]. Journal of Composites for Construction,2012,16(3):245-252. [9]YANG X,YANG Z,W EN Q,et al.Bending of simply-supported circular timber beamstrengthened with fiber reinforced polymer[J].Applied Mathematics and Mechanics,2014,35(3):297-310. [10]TRIANTAFILLOU T C.Composites:a new possibility for the shear strengthening of concrete, masonry and wood[J].Composites Science and Technology,1988,58(8):1285-1295. [11]TRIANTAFILLOU T.Shear reinforcement of wood using FRP materials[J].Materials in Civil Engineering,1997,9(2):65-69. [12]AKBIYIK A,LAMANNAAJ,HALE W M,et al.Feasibility investigation of the shear repair of timber stringers with horizontal splits[J].Construction and Building Materials,2007,21(5): 991-1000. [13]MANALO AC,ARAVINTHAN T,KARUNASENAW,et al.Flexural behaviour of structural fibre composite sandw ich beams in flatw iseand edgew ise positions[J].Composite Structures,2010, 92(4):984-995. [14]杨骁,姜莹莹.纤维增强聚合物加固带裂缝矩形截面木梁的弯曲[J].应用力学学报,2012,29(5): 516-522. [15]PLEVRISN,TRIANTAFILLOUT C.Creepbehavior of FRP-reinforced woodmembers[J].Journal of Structural Engineering,1995,121(1):174-186. [16]PLEVRISN,TRIANTAFILLOU T C.Time-dependent behavior of RC members strengthened with FRP laminates[J].Journal of Structural Engineering,1994,120(3):1016-1042. [17]DAVIDSW G,DAGHERH J,BRETON JM,et al.Modeling creepdeformationsof FRP-reinforced glulambeams[J].JournalW ood and Fiber Science,2000,32(4):426-441. [18]YAHYAEI-MOAYYED M,TAHERI F.Creepresponse of glued-laminated beamrein forced with pre-stressed sub-laminated composite[J].Construction and Building Materials,2011,25(5): 2495-2506. [19]YAHYAEI-MOAYYED M,TAHERI F.Experimental and computational investigations into creepresponse of AFRP reinforced timber beams[J].Composite Structures,2011,93(2):616-628. [20]陆伟东,宋二玮,岳孔,等.FRP板增强胶合木梁蠕变性能试验研究[J].建筑材料学报,2013,16(2): 294-297. [21]LUW D,SONG E,HEM,et al.Experimental study on bending creepbehaviour of reinforced glulambeam[C]//Proceedings of the 12th W orld Conference on T imber Engineering.2012. [22]PULNGERN T,KAEWKALYAP,ROSARpITAK V,et al.Experimental and computational investigations of creepresponses of wood/PVC composite members[J].International Polymer Processing,2014,29(3):307-316. [23]CHRISTENSENR M.Theory of viscoelasticity,an introduction[M].2nd ed.New York:Academic Press Inc,1982:1-33. Analy tical solu tion of bend ing of v iscoelastic timber beamrein forced with fi ber rein forced po lymer sheet OUYANG Yu,JIANG Yong,ZHOU Lei Regarding timber beamas a viscoelastic mediumwith a standard linear solid constitutive relation,and assuming bonding tightly between the fiber reinforced polymer (FRP)sheet and timber beam,the creepbehavior of linear bending of the timber beamreinforced with FRP sheet is studied.Based on the estab lished governing equation for bending deformation of the viscoelastic rectangular cross-section timber beamreinforced with FRP sheet,ananalytical solution of bending of the simply-supported FRP-reinforced viscoelastic timber beamsub ject to stepuniformload is presented by using Laplace transform.The material parameters of the standard linear solid constitutive relation for Douglas-fi r(DF) timber are determined with existing experimental data.The influences of volume fraction of aramid FRP(AFRP)sheet and span-depth ratio of beamon the bending behavior of the simply-supported DF timber beamreinforced with AFRP sheet is analyzed numerically. It is shown that creepdeflections of the DF timber beamcan be eff ectively decreased by AFRP sheet reinforcement.W ith development of creepof the DF timber beam,the neutral axis of the DF timber beamreinforced with AFRP sheet moves to the edge of the timberbeamof bonding AFRP sheet.Furthermore,with increase of the span-depth ratio of DF timber beamand volume fraction of AFRP sheet,maximumcompressive and tensional stresses of the AFRP-reinforced DF timber beamdecrease. fiber reinforced polymer(FRP);reinforcement;timber beam;viscoelasticity; analytical solution TU 323.3;O 344.6 A 1007-2861(2017)04-0609-14 DO I:10.12066/j.issn.1007-2861.1664 2015-09-07 国家高技术研究发展计划(863计划)资助项目(2009AA032303-2) 欧阳煜(1968—),男,副教授,博士,研究方向为组合结构、结构加固与修复研究. E-mail:Oyy w ly@sina.com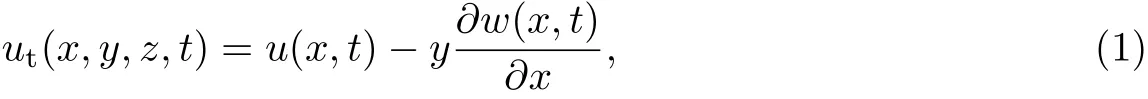

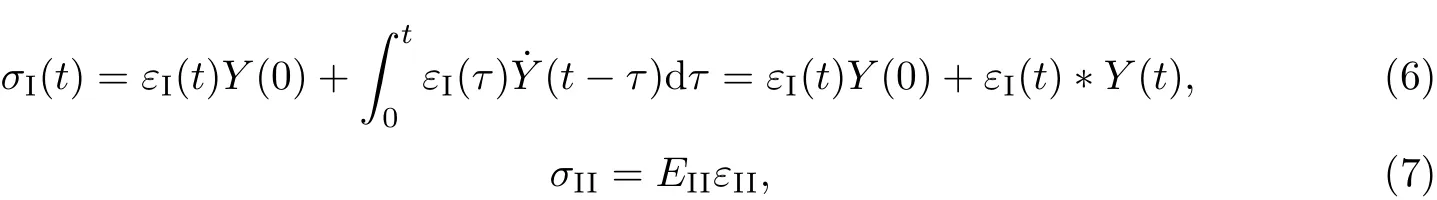
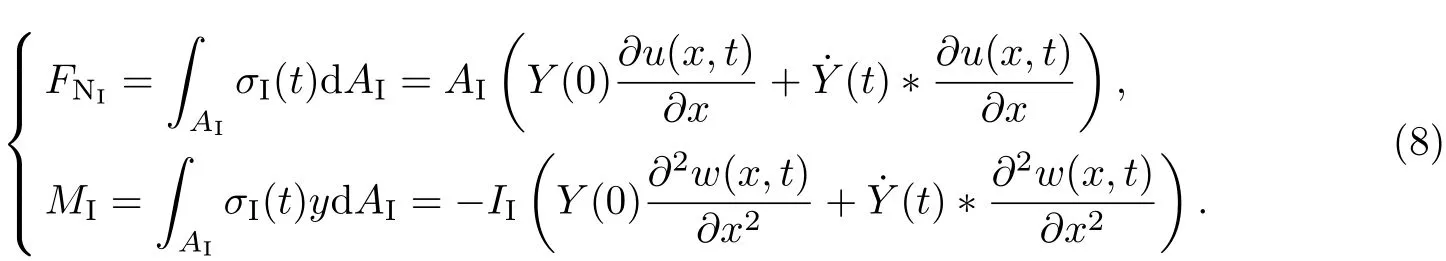
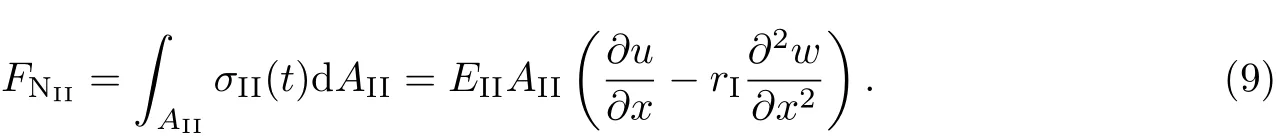

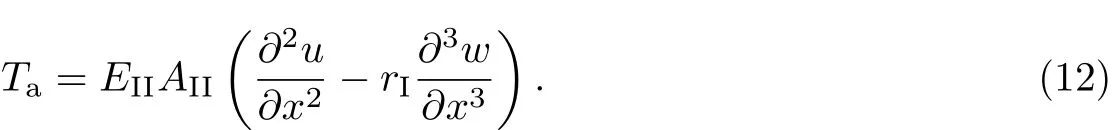
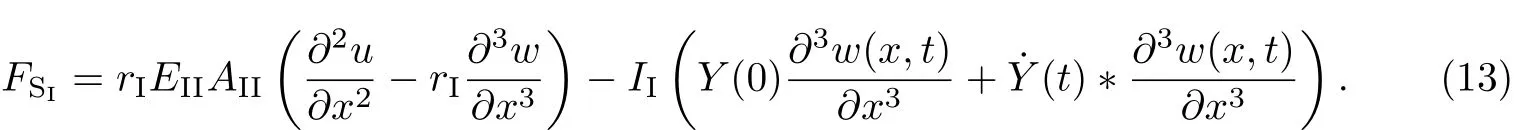

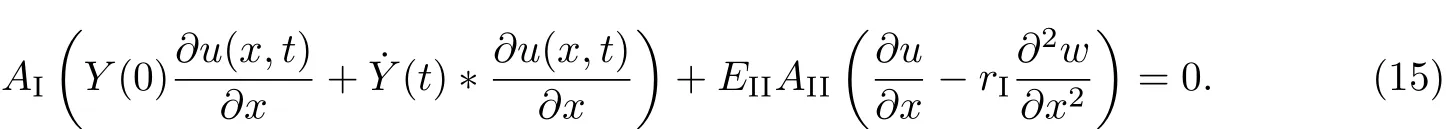
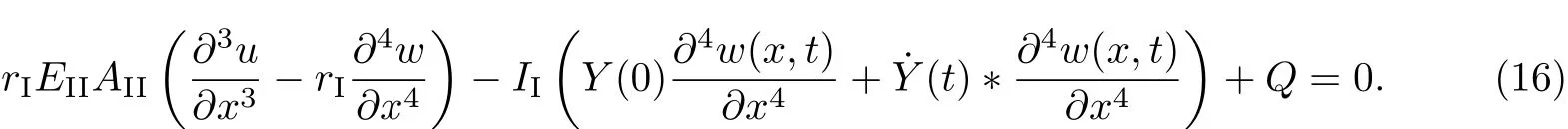
2 突加均布载荷作用下FRP布加固简支黏弹性木梁的弯曲解析解
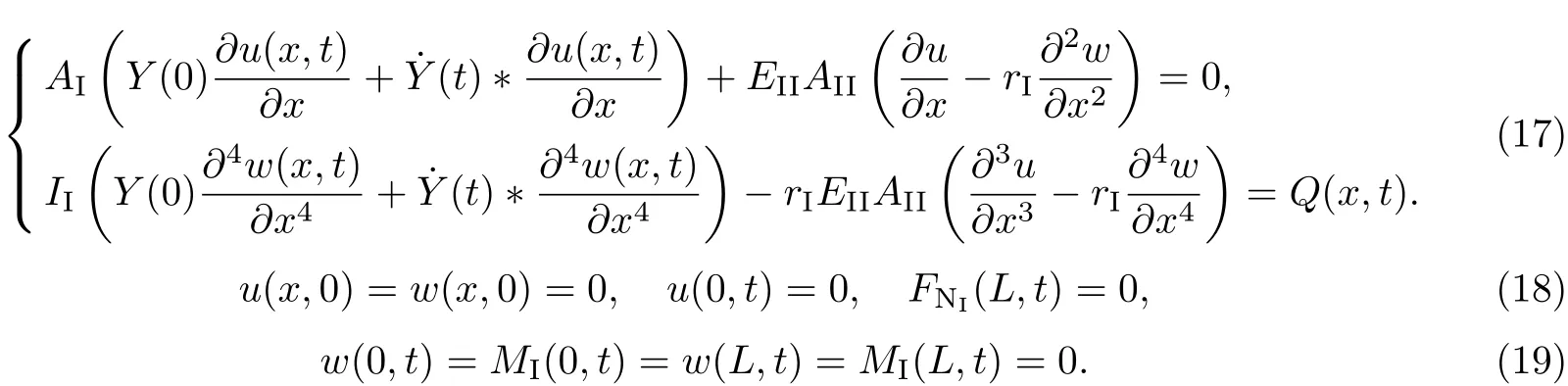



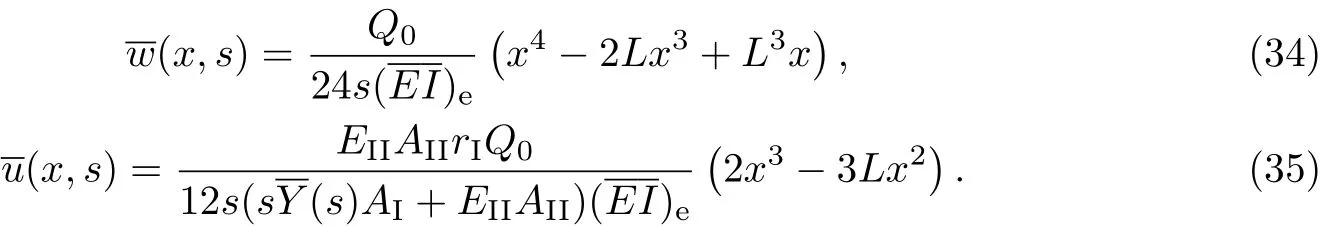


3 参数分析



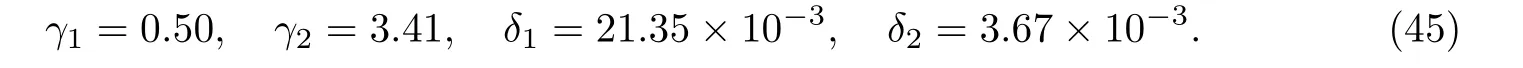

4 结论

(Department of Civil Engineering,Shanghai University,Shanghai 200444,China)

