一类(α,m)-凸函数的H adamard型不等式
李玉娇,杜廷松,2
(1.三峡大学理学院,湖北宜昌443002; 2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,武汉430081)
一类(α,m)-凸函数的H adamard型不等式
李玉娇1,杜廷松1,2
(1.三峡大学理学院,湖北宜昌443002; 2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,武汉430081)
首先,提出了一个新的积分恒等式;然后,在此基础上构造了一类二阶导函数的绝对值的q次幂是(α,m)-凸函数的新型Hadamard型不等式;最后,给出了一些具体的应用例子.
凸函数;(α,m)-凸函数;Hadamard型不等式
设f:I⊆R→R是一个凸函数,a,b∈I且a 众所周知,这是经典的Hermite-Hadamard型凸函数不等式.已有很多学者对各种广义凸函数不等式进行了改进和推广[1-5].1978年,Breckner[6]介绍了s-凸函数;1984年,Toader[7]定义了一类m-凸函数;1993年,Mihe¸san[8]介绍了(α,m)-凸函数. 随着不等式研究的发展,Hadamard型不等式在凸分析领域中的研究有了显著的进展.已有众多学者研究了诸如凸函数[9]、s-凸函数[10]、m-凸函数[11]以及(α,m)-凸函数[12-14]的Hadamard型不等式.此外,还有一些学者针对(α,m)-对数凸函数[15]、(α,m)-几何凸函数[16]和(α,m)-预不变凸函数[17]的Hadamard型不等式进行了研究. 本工作基于文献[10,18-19]中研究s-凸函数的Hadamard型不等式的构造性思想,并受文献[11,14]中涉及的m-凸性和(α,m)-凸性的Hadamard型不等式研究问题的启发,研究了一类(α,m)-凸函数的Hadamard型不等式,并提出了一个新的不同于文献[10]的积分恒等式.需要强调的是,尽管本工作与文献[10]均是对f(x)二阶导函数Hadamard型不等式的研究,但是本工作研究的是(α,m)-凸函数,而文献[10]研究的是s-凸函数.另外,本工作与文献[14]均是研究(α,m)-凸函数的Hadamard型不等式,但文献[14]考虑的是Hadamard型不等式(1)的右边部分,而本工作是对式(1)左边部分的上界进行研究.也就是说,本工作获得的主要结果是文献[10-11,14]中已有结果的延伸和推广. 在本工作中,考虑实区间I⊆R=(-∞,∞),I◦表示区间I的内部. 定义1[8]函数f:[0,b]→R被称为(α,m)-凸函数,如果对任意的x,y∈[0,b],t∈[0,1]且(α,m)∈[0,1]2,有下面的式子成立: 易知当(α,m)∈{(0,0),(α,0),(1,0),(1,m),(1,1),(α,1)}时,这类(α,m)-凸函数分别是增函数、α-starshaped函数、starshaped函数、m-凸函数、凸函数和α-凸函数. 定理1[10]设函数f:I⊂[0,∞)→R是I◦上的一个可微映射,f′′∈L[a,b],其中a,b∈I且a 推论1[10]在定理1中,当s=1时,有下面的不等式成立: 引理1设f:I⊆R0→R是定义在I◦上的一个二次可微映射,a,b∈I◦.对于一些固定的m∈(0,1],mb>a,如果f′′∈L[a,b],则有下面的等式成立: 利用分部积分,得到 故式(5)成立.证毕. 定理2设f:I⊆R0→R是定义在I◦上的一个可微映射,a,b∈I◦,f′′∈L[a,b].对于一些固定的(α,m)∈(0,1]2,mb>a且q≥1,如果|f′′|q是定义在[a,b]上的(α,m)-凸函数,则 假设q>1,依据引理1以及Power-Mean积分不等式,有 和 成立. 由于|f′′|q是[a,b]上的(α,m)-凸函数,对任意的t∈[0,1],有 由式(7)~(10),可得 故不等式(6)成立.证毕. 推论2在定理2中,当α=m=q=1,则 这里需要强调的是,不等式(11)与文献[10]中定理2之推论1(见式(4))相比是一个改进结果. 定理3设f:I⊆R0→R是定义在I◦上的一个可微映射,a,b∈I◦,f′′∈L[a,b].对固定的(α,m)∈(0,1]2,mb>a,q>1,如果|f′′|q是定义在[a,b]上的(α,m)-凸函数,则 证明依据引理1以及H¨older’s不等式,有 故不等式(12)成立.证毕. 推论3在定理3中,当α=m=1,则 考虑如下平均值. (1)算术平均值. (2)对数平均值. (3)广义对数平均值. 根据上述结果,给出一些具体应用例子. 命题1设n∈(-∞,0)∪[1,∞){-1},[a,b]⊂[0,b∗]且b∗>0,则 证明将f(x)=xn应用到推论2,即获得不等式(14). 命题2设n∈(-∞,0)∪[1,∞){-1},[a,b]⊂[0,b∗],b∗>0且q>1,则 证明将f(x)=xn应用到推论3,即获得不等式(15). [1]春玲,双叶.协同s-凸函数的Hermite-Hadamard型积分不等式[J].内蒙古民族大学学报,2013, 28(6):627-630. [2]何晓红,许谦.AH凸函数的几个积分不等式及其应用[J].上海大学学报(自然科学版),2014,20(3): 368-373. [3]D RAGOMIR SS.Hermite-Hadamard inequalities for operator convex functions[J].Applied Mathematics and Computation,2011,218(3):766-772. [4]C HEN F X,F ENG Y M.New inequalities of Hermite-Hadamard type for functions whose fi rst derivatives absolute values are s-convex[J].Italian Journal of Pure and Applied Mathematics, 2014,32:213-222. [5]L I S J,Z HAO L Z,L ENG G S.Inequalities for Tφ-convex functions[J].Journal of Shanghai University(English Edition),2007,11(2):142-147. [6]B RECKNER W W.Stetigkeitsaussagen f¨ur eine k lasse verallgemeinerter konvexer funktionen in topologischen R¨aumen[J].Publications of the Institute for Mathematical,1978,23:13-20. [7]T OADER G.Some generalizations of the convexity[C]//Proceedings of the Colloquiumon Approximation and Optimization.1984:329-338. [8]MIHES¸AN V G.Ageneralization of the convexity,seminar on functionar on functional equations[M].Romania:Approximation and Convexity,Cluj-Napoca,1993. [9]C HUN L,Q I F.Integral inequalities of Hermite-Hadamard type for functionswhose third derivatives are convex[J].Journal of Inequalities and Applications,2013,DOI:10.1186/1029-242X-2013-451. [10]¨O ZDEMIR ME,YıLDıZ C¸,AKDEMIR AO,et al.On some inequalities for s-convex functions and applications[J].Journal of Inequalities and Applications,2013,DOI:10.1186/1029-242X-2013-333. [11]¨O ZDEMIR ME,AVCI M,S ET E.On some inequalities of Hermite-Hadamard type via m-convexity[J].Applied Mathematics Letters,2010,23(9):1065-1070. [12]I S¸CAN I.Anew generalization of some integral inequalities for(α,m)-convex functions[J].Mathematical Sciences,2013,7(1):1-8. [13]W ANG S H,X I B Y,Q I F.On Hermite-Hadamard type inequalities for(α,m)-convex functions[J].International Journal of Open Prob lems in Computer Science and Mathematics, 2012,5(4):47-56. [14]¨O ZDEMIR ME,AVCI M,K AVURMACI H.Hermite-Hadamard type inequalities via(α,m)-convexity[J].Computers and Mathematics with Applications,2011,61(9):2614-2620. [15]D ENG J H,W ANG J R.Fractional Hermite-Hadamard inequalities for(α,m)-logarithmically convex functions[J].Journal of Inequalities and Applications,2013,DOI:10.1186/1029-242X-2013-364. [16]X I B Y,B AI R F,Q I F.Hermite-Hadamard type inequalities for the m-and(α,m)-geometrically convex functions[J].Aequationes Mathematicae,2012,84(3):261-269. [17]L ATIFAMA,S HOAIBB M.Hermite-Hadamard type integral inequalities for diff erentiab le mpreinvex and(α,m)-preinvex functions[J].Journal of the Egyptian Mathematical Society,2015, 23(2):236-241. [18]李玉娇,杜廷松.推广的(s,m)-GA-凸函数的Simpson型不等式[J].纯粹数学与应用数学,2015, 31(5):487-497. [19]Y ANG Z Q,L I Y J,D U T S.Ageneralization of Simpson type inequality via diff erentiable functions using(s,m)-convex functions[J].Italian Journal of Pure and Applied Mathematics, 2015,35:327-338. H adamard-type inequalities for a class of (α,m)-convex functions LIYujiao1,DU Tingsong1,2 This paper proposes an integral identity.Based on the identity,some results of Hadamard inequalities are established for functions with the q-th power of the second derivative’s absolute value(α,m)-convex.Some specifi c applied examples are presented. convex function;(α,m)-convex function;Hadamard-type inequality O 178;O 174.6 A 1007-2861(2017)04-0583-07 DO I:10.12066/j.issn.1007-2861.1716 2015-06-01 国家自然科学基金资助项目(61374028);湖北省自然科学基金资助项目(2013CFA131);三峡大学培优基金资助项目(2015PY 075) 杜廷松(1969—),男,教授,研究方向为凸分析及最优化理论与算法.E-mail:tingsongdu@ctgu.edu.cn
1 预备知识
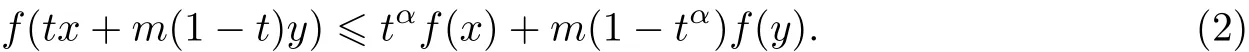
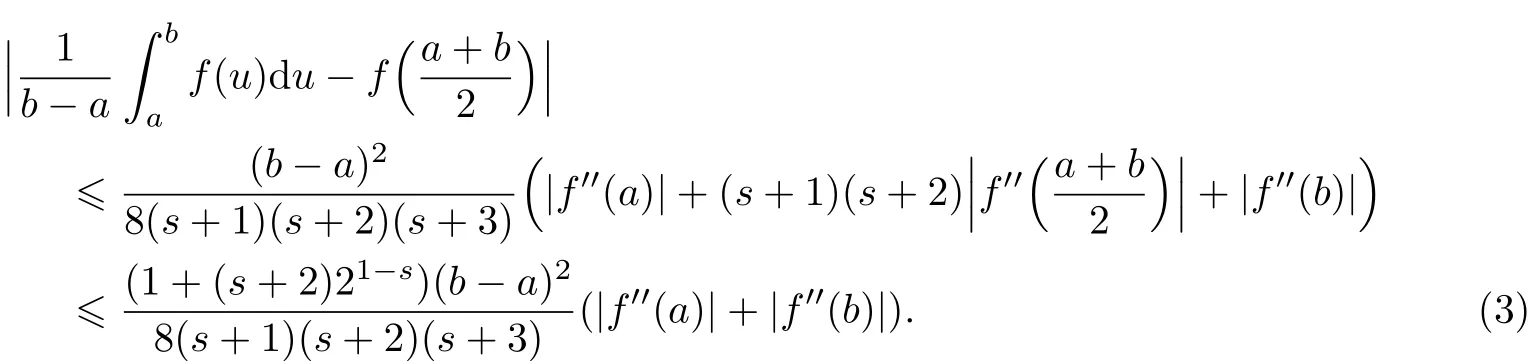

2 一个新引理

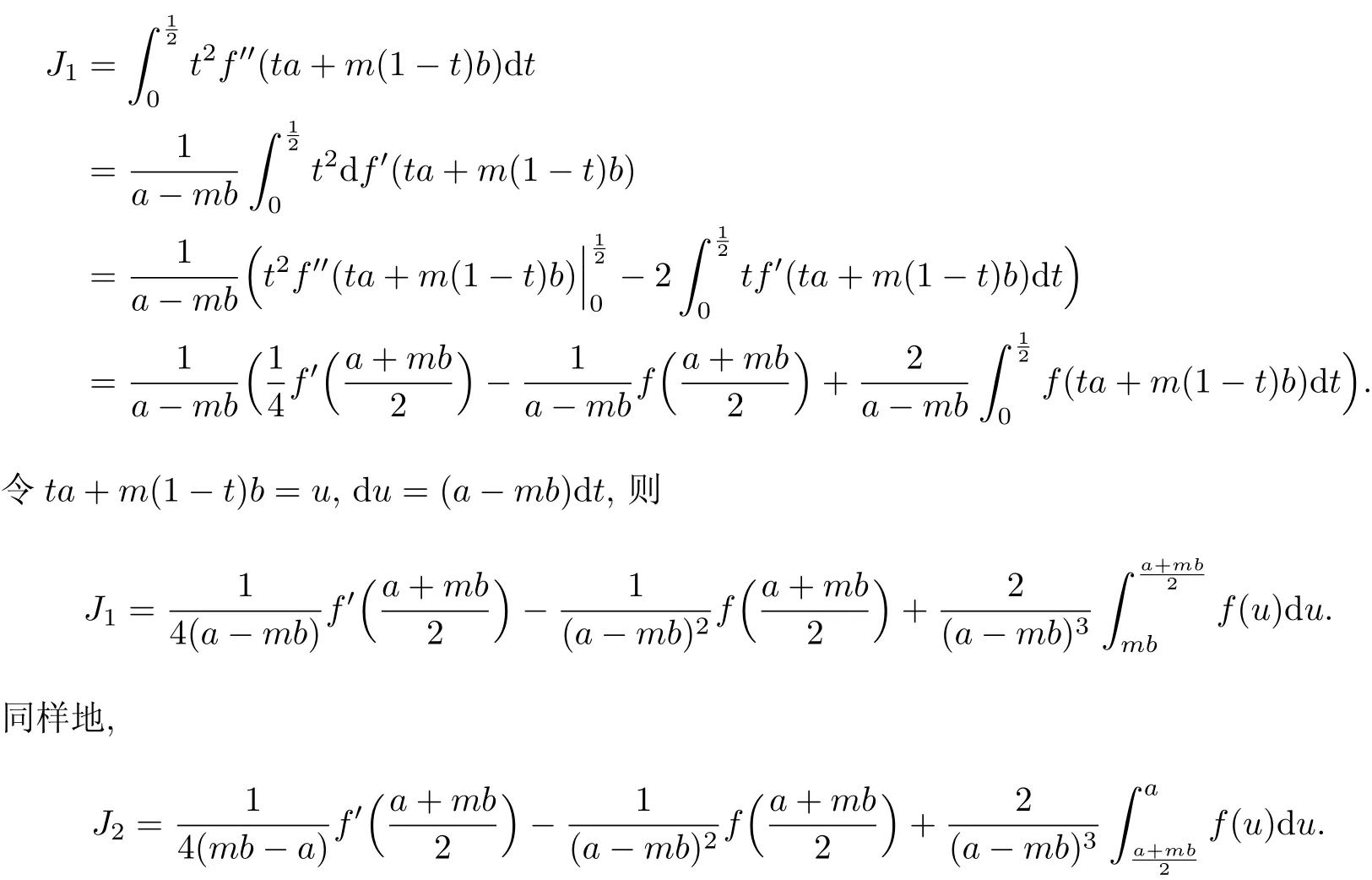
3 新的H ermite-H adamard型不等式





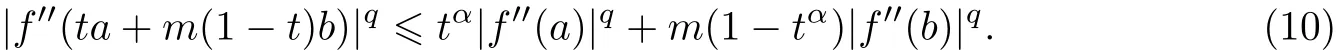

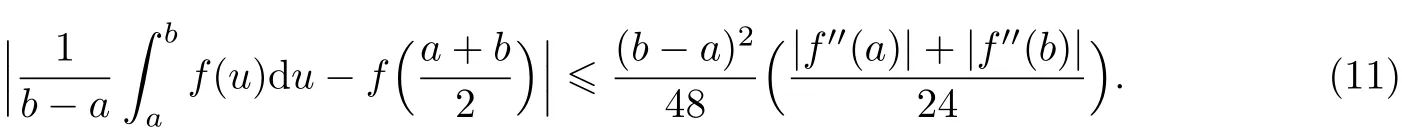



4 应用





(1.College of Science,China Three Gorges University,Yichang 443002,Hubei,China; 2.Hubei Province Key Laboratory of SystemScience in Metallu rgical Process,W uhan University of Science and Technology,W uhan 430081,China)

