基于LPZ谱分析法的非高斯脉动风压模拟

蒋磊,李春祥,邓莹

(上海大学土木工程系,上海200444)

基于LPZ谱分析法的非高斯脉动风压模拟

蒋磊,李春祥,邓莹

(上海大学土木工程系,上海200444)

提出一种基于线性预测和Z转换(linear prediction and Z-transform,LPZ)谱分析法的非高斯脉动风压模拟算法.运用Johnson变换系统实现高斯随机过程到非高斯白噪声的转换;再使用LPZ对其进行数字滤波,进而得到所需的非高斯脉动风压.采用基于LPZ谱分析法对单变量非高斯随机信号和非高斯脉动风压进行了数值模拟.通过对模拟的非高斯信号和脉动风压的统计参数(峰度和偏度)与目标统计参数,以及模拟的功率谱与目标功率谱进行比较,验证了基于LPZ谱分析法的非高斯脉动风压模拟算法的有效性.

非高斯脉动风压模拟;线性预测和Z转换谱分析法;Johnson变换系统;数字滤波

非高斯过程的模拟方法可以分为两类:第一类是根据任意指定的高阶特征统计参数(例如斜度与峰度)及其目标功率谱密度(power spectral density,PSD)函数来实现;第二类是通过任意指定的边缘概率分布函数(probability density function,PDF)及其目标功率谱密度(PSD)函数来实现.Gurley等[1]、Seong等[2]和Suresh等[3]等在20世纪90年代就开始了第一类非高斯过程的模拟研究.Seong等[4]采用指数峰值模型进行了单变量和多变量非高斯风压时程的模拟.Suresh等[3,5]基于快速傅里叶变换(fast Fourier transform,FFT)技术,采用参数较少的指数峰值模型模拟了一维单变量非高斯风压时程,并用于大跨低矮屋盖的风振分析.第一类模拟方法过于繁琐,建立的转换关系往往为非线性,且在建立过程中并没有考虑PSD,因而转换后的PSD可能出现负值.对于第二类非高斯模拟,主要有KLE(Karhunen-Loeve)法[6]和Hermite谱修正法[7-9]等.Yang等[9]通过Hermite PDF模型模拟出了多变量非高斯风压.Ma等[10]提出了基于增强现实(augmented reality,AR)模型与Johnson逆变换的风压模拟方法.第二类模拟通常需要采用迭代算法.然而,随着迭代次数的增加,模拟数值不一定会逐渐逼近目标值,且当迭代到一定次数时,反而可能出现发散现象.针对第一类模拟算法,本工作提出一种基于线性预测和Z转换(linear prediction and Z-transform,LPZ)谱分析法的非高斯脉动风压非迭代模拟算法,简化了已有算法,提高了运算效率与模拟精度.

1 LPZ谱分析法

根据随机过程理论,表征随机变量数学特征的统计参数如下:均值(一阶)µ=w=表∫示随机过程的摆动中心,其中p(w)表示随机过程w的概率密度函数;方差(二阶)表示随机过程在某时刻对于其均值的偏离程度;偏度(三阶)是定量描述独立随机过程与高斯分布偏离程度的基本量;峰表示分布曲线尖峭或平坦的程度.

高斯过程的偏度为0而峰度为3.偏度不为0或峰度不为3的随机过程即为非高斯过程.偏度反映了以其平均值为中心的分布的不对称程度,正偏度表示不对称部分的分布更趋向正值,负偏度表示不对称部分的分布更趋向负值.峰度能够表明时域信号峰值的概率大小,描述了概率密度函数中间部分的尖锐度或平滑度以及尾部的窄度或宽度.当峰度K>3时,表示分布呈高峰度,具有相对多的高峰值和低谷值,此时的非高斯过程称为超高斯随机过程(softening non-Gaussian processes).当K<3时,表示分布呈低峰度,具有相对较少的高峰值和低谷值,此时的非高斯过程称为亚高斯随机过程(hardening non-Gaussian processes).

把离散的随机脉动风压序列{wr|r=0,1,2,···,N-1}作为研究的随机过程,则表征该随机脉动风压的数学统计参数分别为

LPZ谱分析法是FFT的一种替代和改进[11].对于一个有限时间内无限数据序列的离散信号,运用LPZ谱分析法可以避免因FFT的局限性和数据截断所造成的缺陷和误差.尽管FFT被普遍认为是信号从时域转换到频域的最终机制,但LPZ谱分析法具有更为优良的频率分辨率和灵敏度.此外,LPZ谱分析法可降噪且不损失分辨率,这是FFT算法无法达到的.正因为优良灵敏度和高分辨率,LPZ谱分析法替代FFT可获得一些不容易获得的频谱信息,提高了模拟计算的准确性.

线性预测(linear prediction,LP)理论表明,每个复值数据点yn可由如下数值点yn+m的线性组合来求得其近似结果:

式中,am为未知线性系数,M为滤波长度,N为采样点总数.

由式(1)可以推导出无限的数据序列以及由Z转换定义的相应谱函数S(z):

式中,z=exp(-iωτ),1/τ为采样率,ω/2π为频率值.式(2)可以通过式(1)进行简化,得到LPZ谱分析法公式:

同时,式(1)的PSD函数可表示为

2 Johnson变换系统

Johnson变换系统可将高斯过程转变为拥有不同偏度和峰度的非高斯序列.基于统计参数算法,Johnson变换系统产生的频率曲线可用于计算已知四阶统计参数的随机分布.在这一系统中,主要有3种不同形式的频率曲线:无界系统(unbound system),即有界系统(bounded system),即为高斯随机序列,η′′为给定偏度与峰度的非高斯随机序列,γ,δ,ξ和λ为常数,可以通过拟合前四阶参数得到.Hill等[12]给出了求解这些常数的公式.

3 基于LPZ谱分析法的非高斯脉动风压模拟新算法

本工作采用LPZ数字滤波技术[13]和Johnson变换系统,建立基于LPZ谱分析法的非高斯脉动风压模拟新算法.本算法属于第一类模拟,即根据任意指定的高阶特征统计参数(如斜度与峰度)及其目标功率谱密度(PSD)函数来实现非高斯随机过程的模拟.

首先假设{ηr}为一组高斯随机序列,则这组高斯序列可通过有限脉冲响应(finite impulse response,FIR)滤波器表示为

对式(5)的两边分别进行LPZ转换,得到

式中,Ak为高斯序列{ηr}的LPZ转换形式,Wk为wr的LPZ转换形式,Hk为系统的转换方程(或频率特性),具体等式关系为

其中z=exp(-iωτ),r,k=0,1,2,···,N-1.Hk的逆LPZ转换形式,即为滤波因子h:

这二者之间的PSD函数存在如下转化关系:

式中,Sk为所求的非高斯随机序列PSD函数,而Sη为非高斯白噪声随机序列的PSD函数,为常数.随机生成的高斯序列{ηr},通过Johnson变换系统转化成拥有一定偏度SSkη和峰度Kη的非高斯白噪声输入序列.最后输出序列中的偏度SSk和峰度K与输入序列中SSkη和Kη的关系为

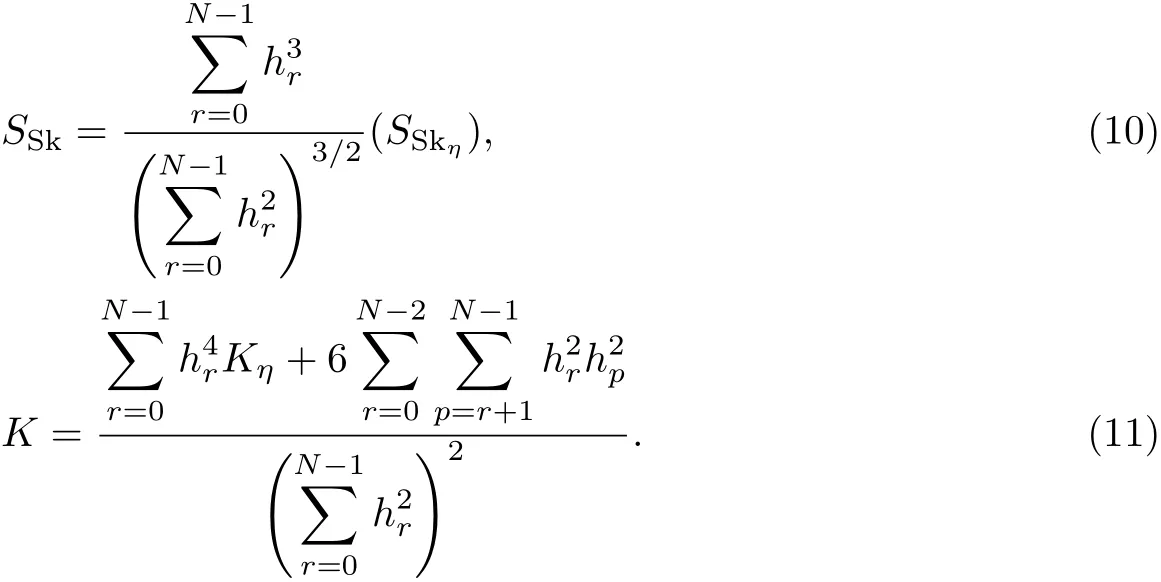
综上所述,为模拟指定偏度SSk、峰度K和PSD函数SSk的非高斯脉动风压,整个模拟过程如下.

步骤1已知Sk,并令Sη=C(C为常数),使用式(9)求解滤波方程

步骤2使用式(8)求解滤波系数hr.

步骤3已知非高斯序列的峰度K和偏度SSk,使用式(10)和(11)求解原输入序列,即求解非高斯白噪声风压时间序列η的偏度SSkη和峰度Kη.

步骤4通过Johnson变换系统,将随机生成的高斯序列{ηr}转换为具有指定偏度SSkη和峰度Kη的非高斯白噪声随机序列η.

步骤5已知η和hr,通过方程(5)对步骤4中求出的非高斯白噪声随机风压η进行降噪处理,求出拥有指定偏度SSk、峰度K和PSD函数SSk的非高斯随机风压.

4 数值验证

4.1 白噪声非高斯信号模拟

首先,对一维单变量白噪声非高斯信号进行模拟,以验证上述方法的有效性.选图1中的目标PSD曲线为所需模拟的非高斯信号目标功率谱密度函数Sk,该频谱为200～500 Hz上的平直谱,均方根值σ约为5.96 g.由于fu=2 000 Hz,根据采样定理确定fs= 5 120 Hz,N=4 096,Δf=1.25 Hz.模拟的目标PSD函数为Sk,目标峰度K=7.0,偏度SSk=-1.10.假设Sη=1,由式(10)得Hk=使用式(11)和(12),求得非高斯白噪声随机序列η的指定偏度SSkη=-2.33,峰度Kη=17.53.

图1 滤波输出后的非高斯白噪声随机序列PSD函数F ig.1 PSD function of the fi ltered non-Gaussian white noise randomsequences

通过Johnson变换系统,使随机生成的高斯序列{ηr}转换为具有指定偏度SSkη和峰度Kη的非高斯白噪声随机序列η,如图2所示.图3为非高斯白噪声随机序列η的PSD函数.

图2 Johnson变换系统产生的非高斯白噪声随机序列F ig.2 Non-Gaussian white noise randomsequences generated by Johnson translator system

经过FIR滤波器的降噪过滤,输出的非高斯脉动风压如图4所示,其偏度和峰度分别为-1.06与7.08,与目标偏度SSk=-1.10和峰度K=7.0相差很小.图1为滤波输出后的非高斯脉动风压的PSD函数与目标PSD函数的对比,发现二者吻合很好.值得指出的是,该信号模拟过程中的功率谱属于分贝频率坐标设置下的形式,与线性频率坐标下的PSD不为负数并不冲突.因此,本工作中非高斯脉动风压模拟将使用线性坐标.

图3 Johnson变换系统产生的非高斯白噪声随机序列PSD函数F ig.3 PSD function of the non-Gaussian white noise randomsequences generated by Johnson translator system

图4 滤波输出后的非高斯白噪声随机序列Fig.4 Filtered non-Gaussian white noise randomsequences

4.2 非高斯脉动风压模拟与算法对比

下面进行一维单变量非高斯脉动风压的模拟.使用李锦华等[14]推导出的脉动风压功率谱方程模拟符合目标脉动风压功率谱、偏度和峰度的非高斯风压.Davenport水平脉动风速功率谱为

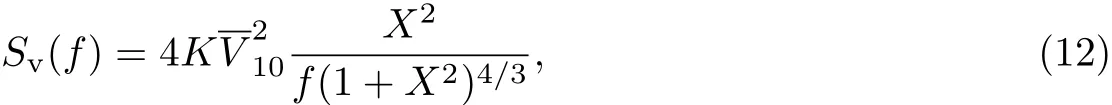
表1 相关模拟参数Tab le 1 Related simu lation parameters

图5为通过Johnson变换系统转换得到的非高斯白噪声风压.图6为非高斯白噪声随机风压的PSD函数.经过FIR滤波器的降噪过滤,输出的非高斯脉动风压如图7所示,其偏度和峰度分别为-2.49与4.77,与目标偏度SSk=-2.4和峰度K=4.8非常接近.图8为滤波输出后的非高斯脉动风压的PSD函数,与目标PSD函数吻合良好.

图5 Johnson变换系统产生的非高斯白噪声脉动风压Fig.5 Non-Gaussian white noise fluctuating w ind pressure generated by Johnson translator system

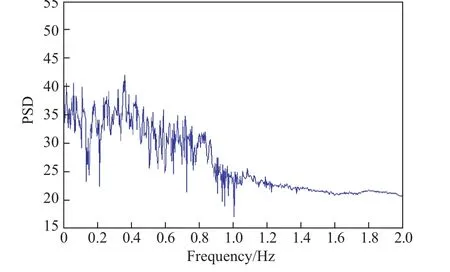
图6 Johnson变换系统产生的非高斯白噪声脉动风压PSD函数Fig.6 PSD function of the non-Gaussian white noise fluctuating w ind pressure generated by Johnson translator system

5 结束语

本工作提出了一种基于LPZ谱分析法的非高斯脉动风压模拟新算法,即运用Johnson变换系统实行高斯随机过程到非高斯白噪声的转换,再使用LPZ谱分析实现了非高斯白噪声谱到目标谱的转化.模拟谱与目标谱基本一致,偏度、峰度值与目标值近似,故而所模拟的非高斯脉动风压与目标风压趋于一致.

图7 滤波输出后的非高斯白噪声脉动风压Fig.7 Filtered non-Gaussian white noise fluctuating w ind pressure

图8 模拟非高斯白噪声脉动风压PSD函数与目标PSD函数的比较Fig.8 Comparisons of the PSD function of the simulated and the target non-Gaussian white noise fluctuating w ind pressure

通过MATLAB编程,使用本算法分别对非高斯随机信号和非高斯脉动风压进行了模拟.通过比较模拟非高斯脉动风压的统计参数(峰度与偏度)与目标统计参数,以及模拟功率谱与目标功率谱,验证了本算法的有效性.

[1]G URLEY K,K AREEMA.Analysis interpretation modeling and simu lation of unsteady w ind and pressure data[J].JournalofW ind Engineering and Industrial Aerodynamics,1997,69:657-669. [2]S EONG S H,P ETERKAJ A.Computer simulation of non-Gaussian mu ltiple w ind press time series[J].Journal ofW ind Engineering and Industrial Aerodynamics,1997,72(1):95-105.

[3]S URESH K K,S TATHOpOULOS T.Synthesis of non-Gaussian w ind pressure time series on low building roofs[J].Engineering Structures,1999,21(12):1086-1100.

[4]S EONG S H,P ETERKAJ A.D igital generation of surface-pressure fluctuations with spiky features[J].Journal of W ind Engineering and Industrial Aerodynamics,1998,73(2):181-192.

[5]S URESH K K,S TATHOpOULOS T.Computer simulation of fluctuating w ind pressures on low building roofs[J].Journal ofW ind Engineering and Industrial Aerodynamics,1997,69(1):485-495.

[6]V OˇRCHOVSK´Y M.Simulation of simply cross correlated randomfields by series expansion methods[J].Structural Safety,2008,30(4):337-373.

[7]Y ANG Q,T IAN Y.Amodel of probability density function of non-Gaussian w ind pressure with multiple samples[J].Journal of W ind Engineering and Industrial Aerodynamics,2015,140: 67-78.

[8]H UANG G,L UO Y,G URLEY K R,et al.Revisiting moment-based characterization for w ind pressures[J].Journal ofW ind Engineering and Industrial Aerodynamics,2016,151:158-168.

[9]Y ANG L,G URLEY K R.Effi cient stationary mu ltivariate non-Gaussian simulation based on a Hermite PDF model[J].Probabilistic Engineering Mechanics,2015,42(4):31-41.

[10]MAX L,X U F Y,K AREEMA,et al.Estimation of surface pressure extremes:hybrid data and simulation-based approach[J].Journal of Engineering Mechanics,2016,DOI: 10.1061/(ASCE)EM.1943-7889.0001127.

[11]T ANG J,N ORRIS J R.LPZ spectral analysis using linear prediction and the Z transform[J]. Journal of Chemical Physics,1986,84(9):5210-5211.

[12]H ILL ID,H ILL R,H OLDER R L.Fitting Johnson curves by moments[J].Applied Statistics, 1976,25:149-176.

[13]H U Y Z,T ONDER K.Simulation of 3-D randomrough surface by 2-D digital fi lter and Fourier analysis[J].International Journal of Machine Tools Manufacturing,1992,32(1/2):83-90.

[14]李锦华,李春祥.土木工程随机风场数值模拟研究的进展[J].振动与冲击,2008,19(9):116-125, 187.

Simu lation of non-Gaussian fl uctuating w ind pressu re based on LPZ spectral analysis

JIANG Lei,LIChunxiang,DENG Ying
(Department of Civil Engineering,Shanghai University,Shanghai 200444,China)

This paper presents an algorithmbased on linear prediction and Z-transform(LPZ)spectralanalysis to simulate non-Gaussian fluctuating w ind pressure.The Gaussian process is converted into a non-Gaussian white noise process by Johnson translator system. The non-Gaussian white noise process is then fi ltered with LPZ spectral analysis to obtain fluctuating w ind pressure.The univariate non-Gaussian randomsignals and non-Gaussian fluctuating w ind pressure are simulated using the algorithm.By comparing the statistical parameters including skewness,kurtosis and power spectral density of the non-Gaussian white noise process and fl uctuating w ind pressure with their target values,it is confi rmed that the algorithmbased on LZP spectral analysis can eff ectively simulate non-Gaussian fluctuating w ind pressure.

non-Gaussian fl uctuating w ind pressure simu lation;linear prediction and Z-transform(LZP)spectral analysis;Johnson translator system;digital fi lter

TU 311

A

1007-2861(2017)04-0600-09

DO I:10.12066/j.issn.1007-2861.1852

2016-09-30

国家自然科学基金资助项目(51378304)

李春祥(1964—),男,教授,博士生导师,博士,研究方向为结构振动控制、结构风工程、结构抗震.

E-mail:Li-chunxiang@vip.sina.com