三叠片压电复合换能器弯曲振动的比较研究

张宁宁



三叠片压电复合换能器弯曲振动的比较研究

张宁宁

(渭南师范学院数理学院，陕西渭南714099)

用瑞利法对三叠片弯振圆盘换能器在三种不同边界条件下的振动特性进行理论研究，推导了谐振频率及有效机电耦合系数的表达式，通过数值计算分析了复合换能器的谐振频率及有效机电耦合系数随换能器各结构参数的变化规律并进行比较研究，同时将计算结果与有限元模拟结果比较，结果表明不同边界条件下换能器的结构参数对谐振频率和有效机电耦合系数影响不同：在换能器结构参数一定时，自由边界条件下谐振频率最大，简支边界条件下最小，固定边界条件下次之；有效机电耦合系数随着金属片厚度、陶瓷片厚度和陶瓷片半径变化时，分别有一个最大值；其他参数一定时，有效机电耦合系数在简支边界条件下最大，自由边界条件下的值稍大于固定边界条件下的值。上述研究结果可为三叠片弯曲振动换能器的设计和实际应用提供一定的理论支持。

瑞利法；谐振频率；有效机电耦合系数；有限元模拟

0 引言

叠片式弯曲振动换能器结构比较简单，辐射面积较大，辐射阻抗较低，易与气体进行阻抗匹配，因此被广泛应用于各种超声领域。文献[1-4]对夹心换能器进行了比较全面的研究。近年来，对叠片式特别是三叠片型换能器的研究和应用受到很多研究人员的重视。文献[5-7]用ANSYS软件对三叠片型换能器在自由和固定边界条件下的振动模态和谐响应进行分析，结果与数值计算结果是一致的。文献[8]用瑞利法对两叠片压电振子在固定边界条件下的谐振频率和有效机电耦合系数进行了数值计算。目前对夹心纵弯模式的换能器研究已比较成熟[9-14]，为了对换能器的性能和机械耦合及结构安装问题进行改善，三叠片式弯曲压电换能器经常被应用，但其边界条件和结构尺寸对换能器的性能影响各不相同而且较大，因此有必要系统地研究叠片式弯曲振动换能器。

弯曲振动是由于同时存在伸长和缩短两种变形所产生，因此可认为弯曲振动是一种间接产生的振动模式，其振动模式相对传统伸缩振动模式和剪切振动模式更为复杂。目前对叠片式弯曲振动的主要研究方法有瑞利变分法和等效电路法，但等效电路法的数学过程相对比较麻烦，所以瑞利法普遍被采用。本文用瑞利法对三种不同边界条件下的三叠片弯振圆盘换能器进行理论研究，推导了谐振频率及有效机电耦合系数的表达式，通过数值计算分析了复合换能器的谐振频率及有效机电耦合系数随各结构参数的变化规律并进行比较，同时与有限元模拟结果比较，得出的结果为叠片式弯曲振动换能器的设计和进一步广泛应用提供理论支持。

1 三叠片弯振圆盘换能器在不同边界条件下频率方程的确定

三叠片弯振圆盘换能器的基本结构如图1所示，由一个金属基片和两个尺寸相同的压电陶瓷片组成，两块压电陶瓷片采用厚度方向极化，然后粘在金属圆盘两个外表面。在压电盘的厚度方向施加电压，压电陶瓷受到激励使上下两个表面产生弯曲振动。图中A为压电圆盘，B为金属圆盘。设是金属圆盘的厚度，为压电片厚度，/2为金属圆盘一半的厚度与压电圆盘厚度之和。为金属圆盘半径，(为半径比)为压电圆盘的半径。利用瑞利原理结合三叠片弯振圆盘换能器的不同边界条件，推导换能器的位移分布函数中的各项系数。设在极坐标中三叠片弯振圆盘换能器的振动位移分布曲线为[15]：

(2)

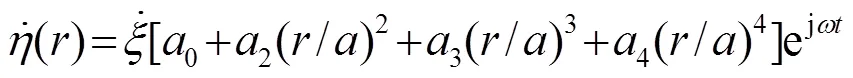
1.1 固定边界条件下频率方程的确定

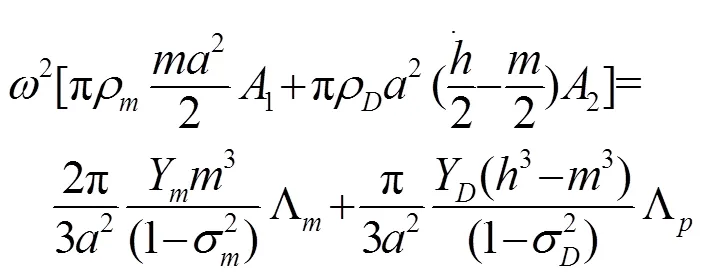
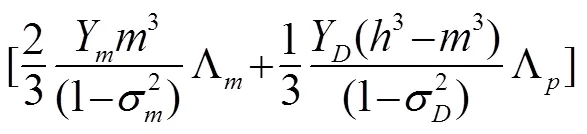
其中，

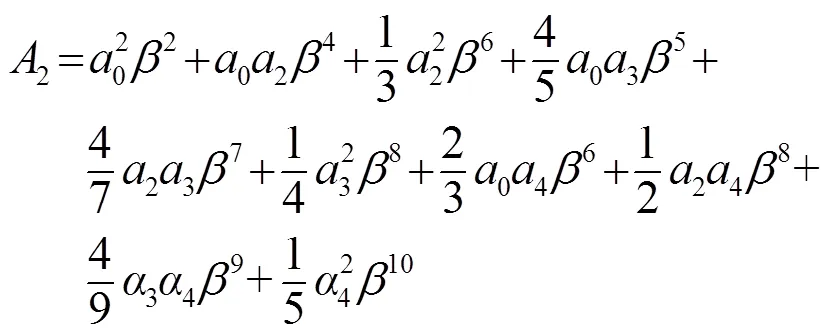
1.2 自由边界条件下频率方程的确定

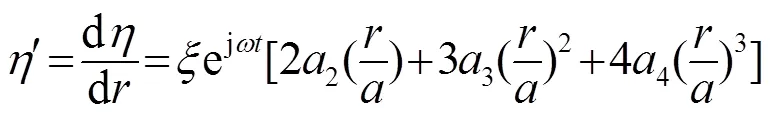
(7)

(8)

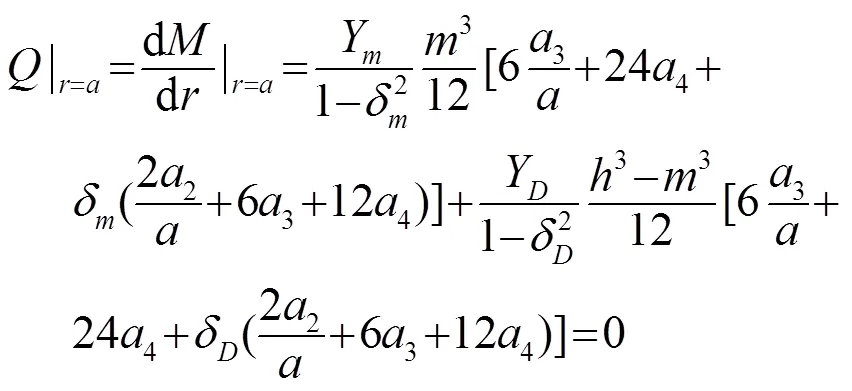
1.3 简支边界条件下频率方程确定

(11)

2 三叠片弯振圆盘换能器的有效机电耦合系数

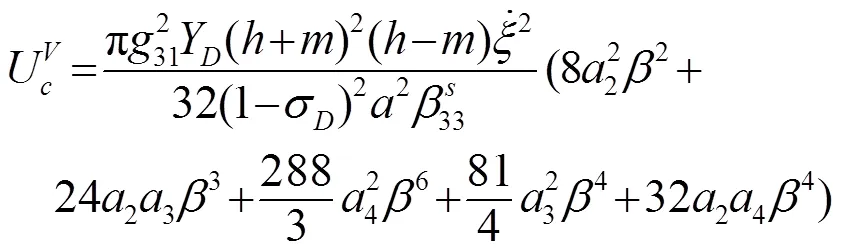
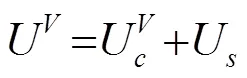
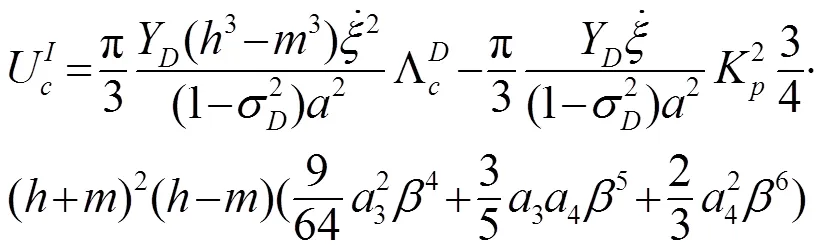
2.3 有效机电耦合系数

对于弯曲压电换能器有效机电耦合系数为[7]

将式(13)和式(15)代入式(16)，可得该换能器的有效机电系数具体表达式。当选定材料后，换能器的各结构尺寸决定了其谐振频率和有效机电耦合系数。谐振频率和有效机电耦合系数的方程比较复杂，解析解很难得到的，所以采用数值计算。以下研究中，取压电材料为PZT-4及金属材料为45号钢，主要材料参数是：

3 不同边界条件下三叠片弯振圆盘换能器谐振频率和有效机电耦合系数与结构尺寸的比较

3.1 不同边界条件下谐振频率的比较

由表1可以看出，三种边界条件下，三叠片弯振圆盘换能器的谐振频率都随着金属片厚度的增大而增大，且在相同的金属片厚度情况下，自由边界条件下频率最大，简支条件下最小，固定条件下次之。自由边界条件下，随着金属片厚度的增大谐振频率变化加快。简支条件下，谐振频率随着金属片厚度的增大，增加量先大后减小。固定边界条件下，谐振频率在金属片厚度的增大量较小时增长很快，约在1.25 mm后随着金属片厚度的增大基本呈线性增长。

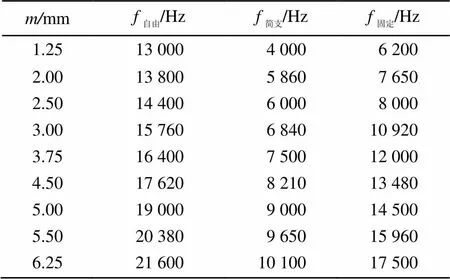
表1 谐振频率随金属片厚度变化

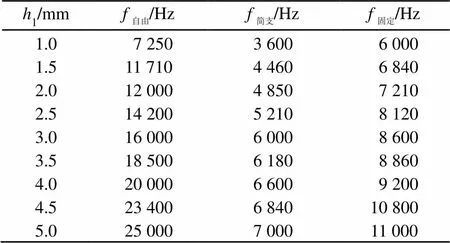
表2 谐振频率随压电片厚度变化

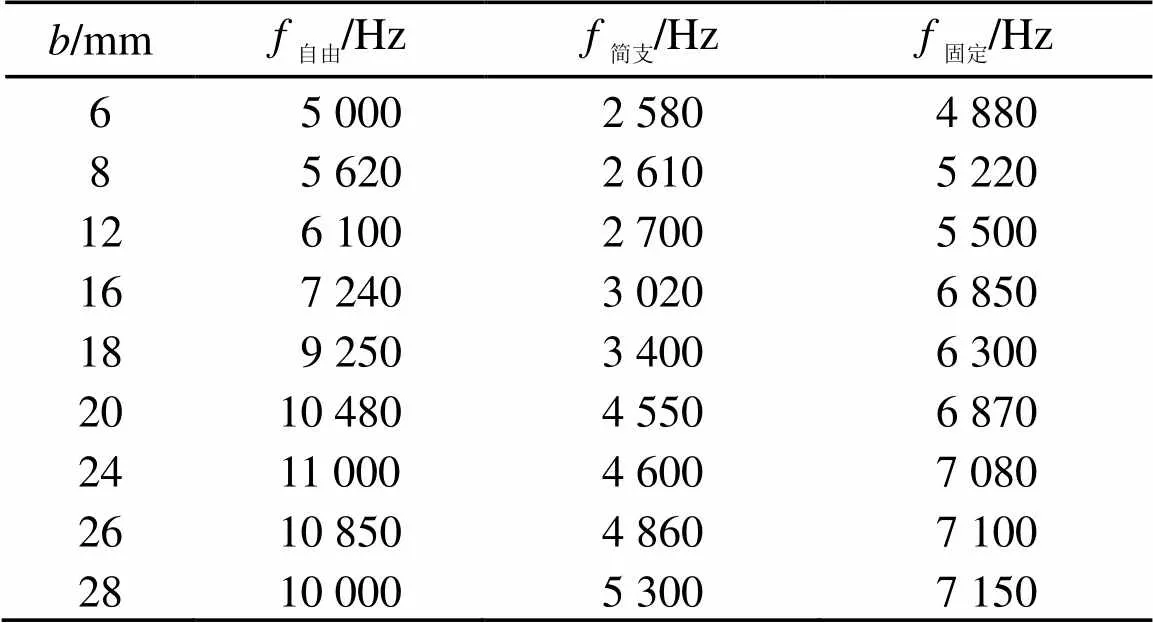
表3 谐振频率随压电片半径变化

由表2可以看出，自由边界条件下，谐振频率随着压电片厚度的增大而增大，且变化趋势不断加剧。简支边界条件下，谐振频率随着压电片厚度的增大也增大，开始变化较快，之后变化有所减缓。但在固定边界条件下，谐振频率一直随压电片厚度的增大而增大。由表3可得，自由边界条件下，谐振频率随着压电片半径的增加先增大后减小，在24 mm附近达到最大，之后有减小的趋势。简支和固定边界条件下的谐振频率都随压电片半径的增大而增大，增长速度越来越快。由表1～3可以看出，在三种边界条件下，若其他参数不变时，谐振频率都随三叠片弯振圆盘换能器结构参数的增大而增大，且都是自由边界条件下频率最大，简支边界条件下最小，固定边界条件下次之。

3.2 不同边界条件下有效机电耦合系数的比较

由图2可看以出，自由边界条件下的有效机电耦合系数先随金属片厚度的增大而迅速增大，之后缓慢减小，在2.5 mm附近达到最佳的机电转换效果，此时耦合系数为0.462。简支边界条件下的有效机电耦合系数在随金属片的厚度增大快速增加，到2.5 mm附近达到最佳的机电转换效果，耦合系数为0.480，之后随着金属片厚度的增大缓慢降低。而固定边界条件下的有效机电耦合系数随着金属片厚度的变化趋势与简支条件类似，但在1.65 mm附近有效机电耦合系数达到最大值，约为0.448。

由图3可看出，自由边界条件下有效机电耦合系数在压电片半径约为22.5 mm时达到最佳的机电转换效果，耦合系数为0.463，之后逐渐降低。简支边界条件下的有效机电耦合系数也随着压电片半径的增大而增大，在半径较小时增长比较缓慢，到达最大值之后增长迅速，在27 mm附近达到最佳的机电转换效果，耦合系数接近0.481。固定边界条件下的有效机电耦合系数随着压电片半径的增大先增大后迅速减小，在压电片半径约为 24 mm时达到最佳机电转换效果，耦合系数约为0.442。

由图4可以看出，自由边界条件下的有效机电耦合系数随着压电片厚度的增大而迅速增大，厚度约为2.0 mm时达到最佳的机电转换效果，耦合系数为0.454，其后又逐渐减小。简支边界条件下，有效机电耦合系数随着压电片厚度的增大而迅速增大，在陶瓷片厚度约为1.4 mm时达到最佳的机电转换效果，耦合系数为0.480。固定边界条件下，有效机电耦合系数随着压电片厚度的增大先快速增大然后缓慢减小，在压电片厚度约为2.8 mm时达到最佳的机电转换效果，耦合系数为0.430。

比较图2、3、4可以进一步得到不同边界条件下的有效机电耦合系数的比较情况。简支边界条件下最大，自由边界条件下次之，固定边界条件下最小。在同一边界条件下，当其他尺寸一定时，有效机电耦合系数随结构参数的变化不同，自由边界时压电片厚度的影响最大，压电片半径的影响最小，金属片厚度的影响次之；简支条件时三种结构参数的影响基本一样；固定边界时，三种结构参数的影响与自由边界时基本相同。

4 有限元分析

在有限元软件Ansys环境下建立换能器有限元模型并分析得到其频率特征和振动模态。在方向上加对称边界条件，相邻压电片之间极化方向相反，在压电片上表面加载荷 Volt=1，在下表面加载荷 Volt=0，然后利用Ansys分别对建立的有限元模型，在自由边界、固定边界和简支边界条件下的三叠片弯振圆盘换能器分别进行模态分析，谐振频率的理论值与模拟值比较结果如表4所示，结合有限元模拟，重点对自由边界条件下谐振频率随压电片半径的变化进行研究，结果如表5所示，表4、5中1为理论计算，2为模拟结果，为理论计算值与模拟值的误差百分比。图5为三种边界条件下的换能器的基频振动模态图。换能器尺寸为、、、。

由图5可看出，三种边界边界条件下，自由边界下中心位移最大，固定边界和简支边界相比固定边界，换能器中心位移相对大些，但边界处的横向位移为零，这些结论与板的振动理论是相符的。由表4可看出，在不同边界条件下，三叠片弯振圆盘换能器的理论计算频率与有限元模拟频率误差较小，仍在工程应用误差允许范围内。理论计算结果与有限元模拟结果存在误差的原因主要是：有限元方法是一个近似方法。有限元法分析一般包括四个步骤：物理模型的简化、数学模型的程序化、计算模型的数值化和计算结果的分析。每一个步骤在操作过程中都或多或少地引入了误差，这些误差的累积就形成最终的误差结果。比如有限元离散化：选不同类型单元 (在相同网格密度下) 所得结果的精度不同以及约束条件和网格划分的密度，都会产生一定误差。由表5可以看出，自由边界条件下，对于不同半径的压电片，其理论计算频率与有限元模拟频率误差较小，比较一致；随着压电片半径的增大即与金属片半径的接近，在＜24 mm范围内换能器的谐振频率一直在增大，当＞24 mm后反而减小，为了保证较高的谐振频率，压电片尺寸不宜选的过大，但是由图3可知，压电片尺寸过小会降低换能器的有效机电耦合系数，因此应综合考虑选择合适的尺寸。其原因是由于压电片半径的增大减小了金属片径向满足自由边界的长度，导致金属基片弯曲振动的有效长度减小，从而影响频率增大，其次压电片半径的增大导致三叠片弯振圆盘换能器的等效刚度增大，从而影响谐振频率升高，因此应综合考虑选择合适的尺寸。

(a) 自由边界

(b) 固定边界

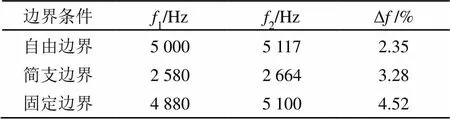
表4 谐振频率的理论计算与模拟值的比较

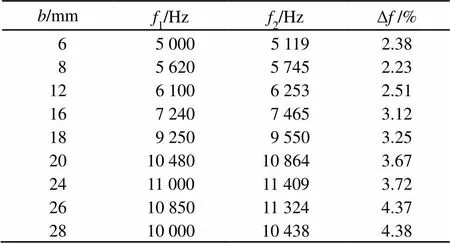
表5 自由边界条件下谐振频率比较

5 结论

用瑞利法对三叠片弯振圆盘换能器在三种不同的边界条件下进行了理论研究，分别推导其谐振频率及有效机电耦合系数表达式，通过数值计算分析了换能器谐振频率及有效机电耦合系数随换能器各结构尺寸参数的变化规律并进行比较，同时将理论计算结果与有限元模拟结果比较，结果表明：

不同边界条件下三叠片弯振圆盘换能器结构参数对谐振频率和有效机电耦合系数影响不同；但在不同边界条件下，换能器结构参数一定时可得到自由边界条件下频率最大，固定边界条件下次之，简支边界条件下最小；有效机电耦合系数随着金属片厚度、陶瓷片厚度和陶瓷片半径变化时，分别都有一个最大值，且进一步得到了不同边界条件下，结构参数对有效机电耦合系数的影响情况为简支边界时最大，自由边界时次之，固定边界时最小。在同一边界条件下，当其他尺寸一定时，有效机电耦合系数随结构参数的变化不同，自由边界时压电片厚度的影响最大，压电片半径的影响最小，金属片厚度的影响次之；简支边界条件时三种结构参数的影响基本一样；固定边界时，三种结构参数的影响与自由边界时的影响基本相同。

就谐振频率而言，三种边界条件中自由边界时频率较其他两种边界都大，就有效机电耦合系数而言，各种情况下的比较结果为简支边界时最大，因此在换能器尺寸一定时，兼顾频率和有效机电耦合系数选择自由边界最佳，而实际应用时应综合考虑不同材料的不同厚度和半径。

在不同边界下的理论计算频率与有限元模拟频率误差较小，比较一致，同时也表明本文理论的正确性，其结论为三叠片弯振圆盘换能器的设计和实际应用提供了一定的理论支持。

[1] 郭林伟, 林书玉, 许龙. 压电换能器静态匹配电路的研究[J]. 纺织高校基础科学学报, 2008, 21(30): 363-367. GUO Linwei, LIN Shuyu, XU Long. Study on the static matching circuit of piezoelectric transducer[J]. Journal of Basic Science in Textile Colleges and Universities, 2008, 21(30): 363-367.

[2] 林书玉. 压电陶瓷矩形薄板振子的弯曲振动研究[J]. 陕西师范大学学报(自然科学版), 1997, 25(1): 39-43. LIN Shuyu. Flexural vibration of piezoelectric ceramic rectangular thin plate[J]. Journal of Shaanxi Normal University (Natural Science Edition), 1997, 25(1): 39-43.

[3] 林书玉. 弯曲振动矩形薄板的辐射声场研究[J]. 声学与电子工程, 2000, 20(3): 13-18. LIN Shuyu. Study on the radiated acoustic field of rectangular thin plate with bending vibration[J]. Acoustics in Electronic Engineering, 2000, 23(3): 13-18.

[4] Piotr CuPial. Three-dimensional natural vibration analysis and consideration for a Piezoelectric rectangular Plate[J].Journal of Sound and Vibration, 2005, 283(10): 1093-1113.

[5] 丁少虎. 小功率弯曲振动换能器的理论及实验研究[D]. 西安: 陕西师范大学, 2008. DING Shaohu. Theoretical and experimental study on small power bending vibration transducer[D]. Xi’an: Shaanxi Normal University, 2008.

[6] 李丹, 卢贵武, 王东. 三叠片换能器的仿真与测试[J]. 内蒙古师范大学学报(自然科学版), 2013, 42(4): 417-423.LI Dan, LU Guiwu, WANG Dong. Simulation and test of three laminated transducer[J]. Journal of Inner Mongolia Normal University (Natural Science Edition), 2013, 42(4): 417-423.

[7] 阚君武, 吴一辉, 宣明, 等. 泵用圆形的分析[J]. 机械工程学报, 2005, 41(1): 54-59. KAN Junwu, WU Yihui, XUAN Ming, et al. Flexural vibration analysis of two laminated circular piezoelectric vibrator for pump[J]. Journal of Mechanical Engineering, 2005, 41(1): 54-59.

[8] 林书玉. 弯曲振动压电陶瓷换能器[J].压电与声光, 1994, 16(5): 27-30. LIN Shuyu. Flexural vibration piezoelectric ceramic transducer[J]. Piezoelectric and Sound Light, 1994, 16(5): 27-30.

[9] 林书玉, 张福成. 模式转换弯曲振动超声换能器的研究[J]. 应用声学, 1994, 13(1): 37-39. LIN Shuyu, ZHANG Fucheng. Study on mode conversion bending vibration ultrasonic transduce[J]. Applied Acoustics, 1994, 13(1): 37-39.

[10] 臧怀刚, 刘广, 李永川. 基于空间冲激响应的圆形换能器辐射声场研究[J]. 压电与声光, 2015, 32(5): 21-25. ZANG Huaigang, LIU Guang, LI Yongchuan. Research on radiation acoustic field of circular transducer based on spatial impulse response[J]. Piezoelectric and Sound and Light, 2015, 32(5): 21-25.

[11] ShuyuLin. Studyon the high Power ai-coupled ultrasonic compound transducer[J]. Ultrasonics, 2006, 44(8): 545-548.

[12] 林书玉. 弯曲振动超声换能器的振动特性及辐射声场研究[J]. 陕西师范大学学报(自然科学版), 2003, 31(3): 32-39. LIN Shuyu. Study on vibration characteristics and radiated sound field of flexural vibration ultrasonic transducer[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2003, 31(3): 32-39.

[13] 张光斌, 林书玉. 气介弯曲振动换能器的辐射声压及指向特性[J]. 陕西师范大学学报(自然科学版), 1999, 27(3): 26-49. ZHANG Guangbin, LIN Shuyu. Radiated sound pressure and directivity of a gas - induced bending vibration transducer[J]. Journal of Shaanxi Normal University (Natural Science Edition), 1999, 27(3): 26-49.

[14] 林书玉. 弯曲振动气介式超声换能器的振动特性及辐射声场研究[J]. 声学与电子工程, 2004, 24(6): 1-7. LIN Shuyu. Study on vibration characteristics and radiated sound field of flexural vibration air borne ultrasonic transducer[J]. Acoustics and Electronic Engineering, 2004, 24(6): 1-7.

[15] 张宁宁, 吴胜举, 凌小娜. 压电陶瓷三叠片复合换能器弯曲振动特性研究[J]. 压电与声光, 2015, 37(4): 620-624. ZHANG Ningning, WU Shengju, LING Xiaona. Study on flexural vibration characteristics of piezoelectric ceramic three composite transducer[J]. Piezoelectric and Sound and Light, 2015, 37(4): 620-624.

Research on flexural vibration characteristics of three laminated piezoelectric transducers

ZHANG Ning-ning

(Mathematics and Physics institute, Weinan Teachers University, Weinan 714099,Shaanxi,China)

Three laminated plate transducer is studied under three different boundary conditions and the expressions of the resonant frequency and the effective electromechanical coupling coefficient are derived by using Rayleigh method. Transducer resonant frequency and effective electromechanical coupling coefficient are analyzed and compared with the variation of the structure parameters of the transducer by means of numerical calculation, and the calculated results are compared with the results of finite element simulation. The results show that the effects of structural parameters under different boundary conditions of the transducer on the resonance frequency and the effective electromechanical coupling coefficient are different: for fixed structural parameters of the transducer, the resonant frequency is the greatest in free boundary condition, the next in fixed boundary condition and the minimum in simply supported boundary condition; the effective electromechanical coupling coefficient varies with the thickness of sheet metal and the thickness and radius of ceramic piece, and each has a maximum value; when other parameters are certain, the effective electromechanical coupling coefficient is the greatest in simply supported boundary condition, and the coefficient value in the free boundary condition is slightly larger than that in the fixed boundary condition. The above-mentioned results provide a theoretical support for the design and application of three laminated bending vibration transducer.

Rayleigh method; resonant frequency; effective electromechanical coupling coefficient; finite element simulation

TB556 P 631.5

A

1000-3630(2017)-04-0383-07

10.16300/j.cnki.1000-3630.2017.04.015

2016-12-19;

2017-03-30

国家自然科学基金资助项目(11074158)、陕西省军民融合研究基金项目(17JMR35)、渭南师范学院校级项目(17YKS08)、渭南师范学院校级教改项目(JG201648)

张宁宁(1978－), 女, 陕西西安人, 硕士, 讲师, 研究方向为功率超声及声学测量。

张宁宁, E-mail: zhangning7892@163.com