相关函数算法在超声导波计量管道内液体流速中的应用
张易农,张克,宋振华,程耀华,彭静,瞿蒙,姚敏,郑睿
相关函数算法在超声导波计量管道内液体流速中的应用
张易农1,张克1,宋振华2,程耀华1,彭静1,瞿蒙1,姚敏1,郑睿1
(1.北京市计量检测科学研究院,北京100029;2.北京工业大学,北京100124)
通过对超声导波技术在充液管道内流量计量的研究,提出了一种新的供热管路中热量表流量计量在线检测方法。试验中,因超声导波在充液管道内传播速度较快,为了准确地测量管道内液体流速对导波传播速度的影响,需要非常准确地提取导波的传播时间。分析了相关函数法在计算导波传播时间的应用原理,并通过理论分析和实验验证了相关函数法的准确性,为采用超声导波测量管道内液体流量提供理论基础。
超声导波;热量表;相关函数法
0 引言
管型结构被广泛应用于石油、化工、市政基础设施中,大多数管道内输送的液体作为载能工质,其实际流量需要精确计量。以市政供暖计量用的超声波热量表为例,流量计量的准确度直接影响热量的计算。因热量表所安装的传输管道内径恒定,所以流量的计算只与管道内液体流速及导波信号传播时间有关。Sato[1]等人对充液管道内液体流动时超声导波的传播特性进行了数值和实验分析,提出了采用超声导波测量管道内液体流量的方法。刘洁[2]从理论与实验两方面研究了基于超声导波技术的小管径管道流量测量方法,初步研究表明,管中水的流速会引起超声导波传播速度的线性变化。然而超声波在水中的传播速度为1500m/s,而充液管道中超声导波非频散段的传播速度可以达到5000m/s[3]。因此采用超声导波纵向模态对流体流量进行测量时,如何准确地提取导波在充液管道的传播时间成为问题的关键所在。本文采用相关函数法计算导波的传播时间,可以更加精确地确定充液管道中导波传播速度与液体流速的关系。
1 充液管道中的导波模态
管道中的导波有三种传播模态:纵向轴对称(L模态)、非轴对称弯曲模态(F模态)和轴对称扭转模态(T模态)。这三种模态的导波分别用(0,)、(,)和(0,)表示,其中代表周向阶次,代表径向模态参数,且均为整数。L模态和T模态是轴对称,F模态是非轴对称模态。
充液管道柱坐标理论模型如图1所示。液体沿管道中心线轴方向传播,和分别代表管道的内径与外径,表示径向距离。
在位移分量表达式中,=0对应轴对称模态的位移,这时,有无限多个扭转模态和无限多个纵向模态。纵向模态中质点的位移偏振向量在(,)平面内,因此,质点位移的周向分量为零。由于在试验中比较容易激发纵向模态,因此只讨论研究这种纵向轴对称模态的超声导波。
2 实验研究
2.1 实验装置
本次实验在北京市计量检测科学研究院能源所的热能表检定装置上完成。该装置不仅可以在一定范围内调节管道内液体的流速,还可以在一定范围内控制液体的温度和压力。
实验用管道为304不锈钢管,长为1800mm,外径为26.38mm,壁厚为2.52mm。为了产生沿管道轴向传播的纵向模态,采用的探头是长度伸缩型的压电陶瓷片,沿着周向方向,均匀粘贴在管壁上。周向均布的压电陶瓷片可以有效地抑制非轴对称模态,产生轴对称模态。每组阵列含有8片压电陶瓷片,每片的长、宽、高分别为12、3mm和0.5mm。激励及接收用的压电阵列间的中心距离为1092mm。实验装置如图2所示。整套实验装置还包括DPO4054示波器、AFG3021B函数发生器、计算机。
实验选取由Hanning窗调制的5个周期的正弦信号作为激励信号,激励出特定频率的纵向模态。该信号由任意波形发生器输出,激励阵列传感器,在管道中产生沿轴向方向传播的纵向模态,并由另一端的传感器阵列接收,通过多通道示波器进行显示并储存。
2.2 超声导波纵向模态群速度计算
计算导波在介质中传播时间的常用方法是通过提取激励与接收信号波包峰值点进行推导,即将激励信号幅值的最高点作为初始时间,接收信号的第一次回波最大幅值作为接收信号的截止时间点,两点之间的时间间隔即为导波的传播时间。导波在充液管道内的传播速度可以达到5000km/s,而常用管道内液体的流速一般不会超过10m/s。因此采用波包幅值法计算液体流速对于超声导波传播速度误差大、精度低,而且充液管道内信噪比低,对于波包峰值的提取也存在很大的难度。
采用相关函数法计算信号时间延迟,其基本思路是将激励信号以Δ为时间增量,沿时间轴进行平移,并将平移后的信号与接收信号做互相关运算,从而获得激励信号与接收信号随Δ变化的相关函数。当相关系数最大时,激励信号的平移量即为激励信号与接收信号之间的时间延迟。相关函数法计算时间延迟具有较强的抗噪音干扰,因而得到了广泛的应用[4]。公式(1)为两信号互相关系数计算公式[5]:
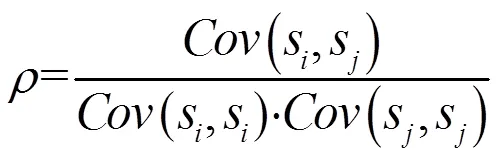
为了避免每次激励信号有所偏差,所以采用相关函数法计算每次接收信号的直达波与激励信号之间的时间差,以此作为导波在激励端与接收端的传播时间。
在管道未充水状态下,激励中心频率为100、110、120、140、150、160kHz和170kHz的由Hanning窗调制的5个周期正弦信号,分别采用波包幅值法与相关函数法计算导波在空心管道内的传播时间,推算导波的传播速度并与理论值做对比,计算结果如表1所示。群速度分布曲线如图3所示,其中实线是空心管道中(0,2)模态理论群速度曲线,正方形为采用相关函数法计算所得(0,2)模态的传播速度,三角形代表采用波包幅值法计算所得导波的传播速度。可以看出,两种算法计算出的群速度变化趋势与理论结果相一致,但采用波包幅值法计算的结果相对于理论值浮动大;通过相关函数法计算的结果与理论值相比,波动相对较小,更接近于导波传播的理论值。
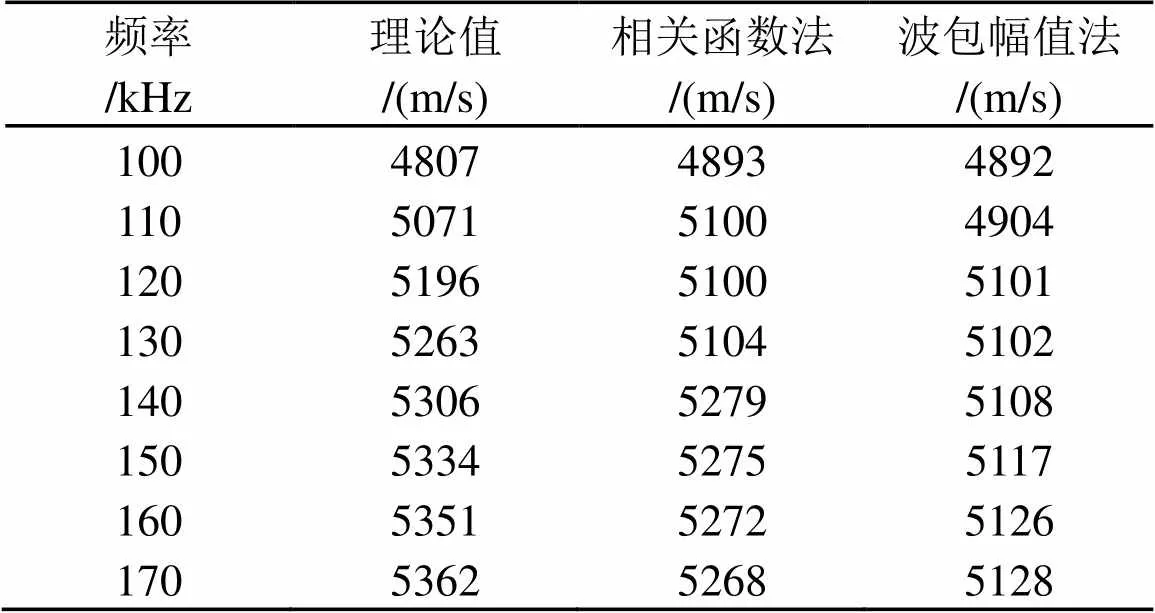
表1 波包峰值法和相关函数法测得空心管道L(0,2)模态群速度值
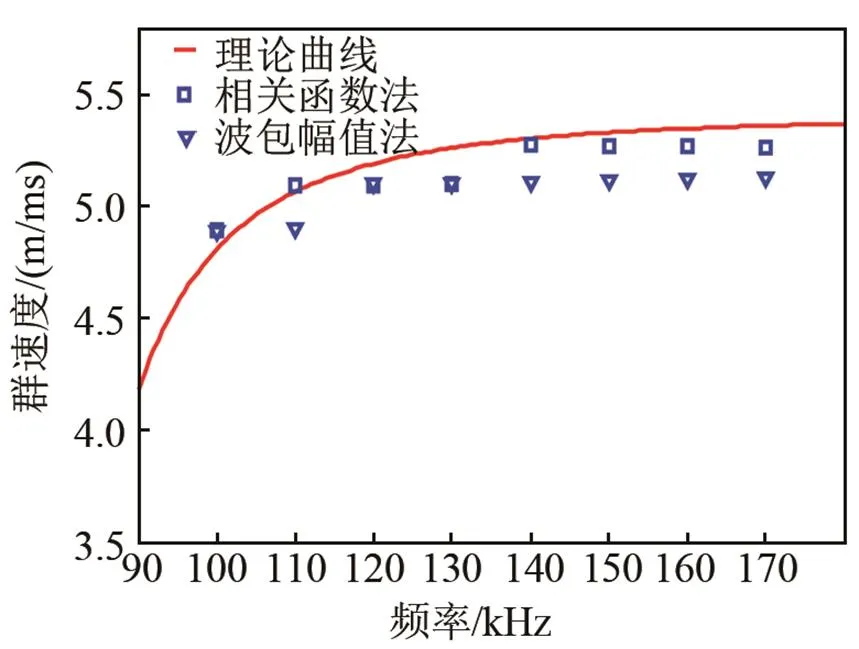
图3 峰值法和相关函数法测得空心管道L(0,2)模态群速度分布曲线
2.3 实验结果分析
实验时,水温控制在42℃,管道内的流量为0.518m3/h。激励信号是中心频率为250kHz的由Hanning窗调制的5个周期正弦信号,接收信号与激励信号作归一化降噪处理,结果如图4所示。可以看出,该激励频率下导波传播频散性不严重,接收信号首次抵达波的波形完整。然而接收信号作降噪处理后存在干扰现象,对采用波包幅值法提取导波传播时间带来很大不便,甚至无法直接获得信号传播时间的信息。
将激励信号与接收信号进行相关处理,结果如图5所示,可以看到相关处理后信号的信噪比更高,波形平整度好,可以直接读取峰值信息。相关函数首次抵达波峰值所对应的时间即为超声导波在激励与接收端的传播时间。调节流量值为典型流量值、、,采用相关算法可以计算导波的传播时间分别为、、。
为了避免声延时对实验结果的影响,以流量5.000m3/h为例计算液体流速对超声导波传播速度的影响,采用相差法计算超声导波在流动液体中的传播时间:
由此可见,管道内的流动液体会对超声导波的传播速度产生一定影响,而采用相关函数法计算波包时间延迟的方法可以获得更可靠、精度更高的结果,为采用超声导波测量管道内液体流量提供理论基础。
3 小结
本文采用相关函数算法计算超声导波在充液管道中的传播时间,相比于常用的波包幅值法精度更高,同时解决了信号信噪比低而无法直接读取波包峰值对应时间点的问题。通过该算法计算管道内不同流量下超声导波的传播时间,可以看出,导波在充液管道内的传播时间与液体的流速有关,为采用超声导波测量液体流量提供基础。
[1] Sato H, Lebedev M, Akedo J. Theoretical investigation of guide wave flowmeter[J]. Japanese Journal of Applied Physics, 2007, 46(7S): 4521-4528.
[2] 刘洁. 基于超声导波技术的小管径管道流量测量方法研究[D]. 北京: 北京工业大学, 2011. LIU Jie. Investigation of flow measurement of small-diameter pipe filled with fluid based on ultrasonic guided wave technique[D]. Beijing:Beijing University of Technology, 2011.
[3] Rose J L著. 固体中的超声波[M]. 何存富译, 北京:科学出版社, 2004.
[4] Cepel R, Ho K C, Rinker B A, et al. Spatial correlation coefficient images for ultrasonic detection[J]. Ultrasonics, Ferroelectricsand Frequency Control, IEEE Transactions on, 2007, 54(9): 1841-1850.
[5] 何存富, 刘岳鹏, 刘增华, 等. 空气耦合 Lamb 波在单晶硅中的传播特性和缺陷检测研究[J]. 机械工程学报, 2015, 51(12): 1-7. HE Cunfu, LIU Yuepeng, LIU Zenghua, et al. Air-coupled lamb waves propagation characteristics and defect detection in monocrystalline silicon[J]. Chinese Journal of Mechanical Engineering, 2015, 54(9):1841-1850.
Application of correlation function method toultrasonic guided wave measurement of liquid flow rate in cylindrical pipeline
ZHANG Yi-nong1,ZHANG Ke1,SONG Zhen-hua2,CHENG Yao-hua1,PENG Jing1, QU Meng1,YAO Min1,ZHENG Rui1
(1.The Measurement Test Research Institute of Beijing, Beijing100029, China; 2. Beijing University of Technology, Beijing 100124, China)
Ultrasonic guided wavepropagation in fluid-filled cylindrical pipeline is investigated in order to put forward a new method of on-line flow measurement for calorimeter in heat-supply pipeline. The propagation speed of ultrasonic guided wave in liquid-filled pipeline is fast. In order to measure the influence of liquid flow rate on the propagation speed of ultrasonic guided wave, it is necessary to extract the propagation time of ultrasonic guided wave accurately. The application of correlation function method to calculating the propagation time of ultrasonic guided wave is introduced, and the accuracy is verified by numerical analysis and experiment. This provides a theoretical basis for applying ultrasonic guided wave to measuring the liquid flow rate in pipeline.
ultrasonic guided wave;ultrasonic heat meter;correlation function
TB95
A
1000-3630(2017)-04-0353-04
10.16300/j.cnki.1000-3630.2017.04.010
2016-08-21;
2016-10-23
张易农(1981-), 男, 北京人, 硕士, 高级工程师, 研究方向为流量及温度计量。
张易农, E-mail: zhangyinong@126.com

