快速预估水下圆形角反射体散射声场的修正声束弹跳方法
梁晶晶,于洋,陈文剑,胡思为,王珲,王艺哲
快速预估水下圆形角反射体散射声场的修正声束弹跳方法
梁晶晶1,于洋2,陈文剑2,胡思为2,王珲2,王艺哲2
(1.中国人民解放军91918部队,北京 100230;2.哈尔滨工程大学水声工程学院,黑龙江哈尔滨 150001)
针对水下圆形角反射体散射声场计算速度问题,在声束弹跳法基础上,提出了一种快速预估散射声场的修正声束弹跳法。对组成圆形三面角反射体的弧形边缘进行离散化,相邻离散点与角反射体顶点构成板块元,并与声源点构成入射声束,利用几何声学计算每条声束在角反射体反射面上的反射,同时得到反射面上每条声束“照射”后再次构成的板块元,用物理声学方法计算所有板块元的散射声场,叠加求和得到整个角反射的散射声场。通过与原始的声束弹跳法计算结果的对比,两者计算结果一致,修正声束弹跳法降低了计算量。
圆形角反射体;多次散射;声束弹跳方法;物理声学方法;几何声学
0 引言
角反射体分为二面和三面角反射体,其中由三个互相垂直的平面组成的角反射体称为三面角反射体,当三个互相垂直的平面为相同的1/4圆面时称为圆形三面角反射体或圆形角反射体。三面角反射体具有在较大空间方位角范围内有较大目标强度的特性,在光学、电磁学和声学中都有广泛的应用。在水声学领域中,角反射体可作为声反射器或水下声学标记物使用,也可作为标准反射体来标定水下目标强度,或作为模拟水下目标回波的声诱饵及实验靶标等[1]。
声波(或电磁波)在角反射体上存在多次散射,目前解决多次散射问题的主要思路之一是把入射波划分为大量入射声束(或射线管),计算每个入射声束的多次散射,然后叠加求和作为整个目标的散射场[2],如电磁波散射领域中的结合等效射线管模型和用物理光学法计算复杂目标高频电磁波多次散射[3],结合射线追踪和电磁流迭代的波束追踪算法[4],以及在图形硬件计算平台上实现的射线弹跳方法[5-6]等;水声学领域中考虑二次散射的修正板块元方法[7]和考虑多次散射的声束弹跳方法[8]。以上方法在计算角反射体散射声场时,都需要利用计算机辅助软件(ANSYS等)划分网格进而划分入射声束,其计算量较大、计算速度较慢。文献[9]中提到了计算角反射体电磁散射的快速算法,但其算法是以角反射体反射面边缘为直线的条件为基础,因此只能计算三角形角反射体或方形角反射体,不能计算角反射体反射面边缘为弧形的圆形角反射体。
本文在声束弹跳法基础上,针对圆形角反射体的特点,提出了一种对角反射体反射面的弧形边缘离散划分的修正声束弹跳法。该方法不需要利用计算机辅助软件进行网格划分,并且具有计算量小、计算速度快的优点。
1 基本理论
计算散射问题的Helmholtz公式为[10]
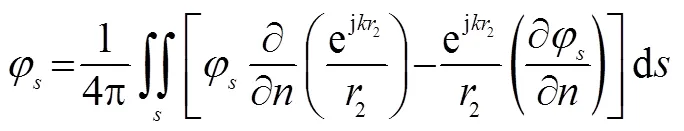
其中:是散射体表面;是表面外法线;是散射点矢径。
在物体表面满足刚性边界条件时,可以得到远场散射势函数:
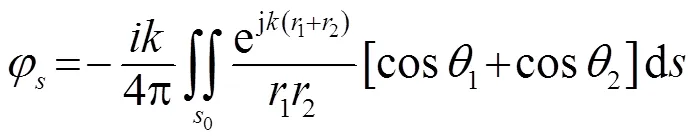
收发合置时变为
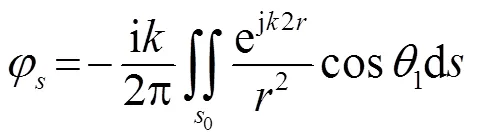
板块元方法是以物理声学方法为基础的高频近似计算方法[11-12]。对于实际的积分曲面,可以将其看作由一定数目的曲面面元叠加而成,对于每个曲面面元,可用一个平面多边形(即板块元)去近似,则该面元的积分值可以用该平面多边形的积分值去近似,而整个曲面的积分值则可以用各平面多边形积分值的累加之和近似。因此有
(4)
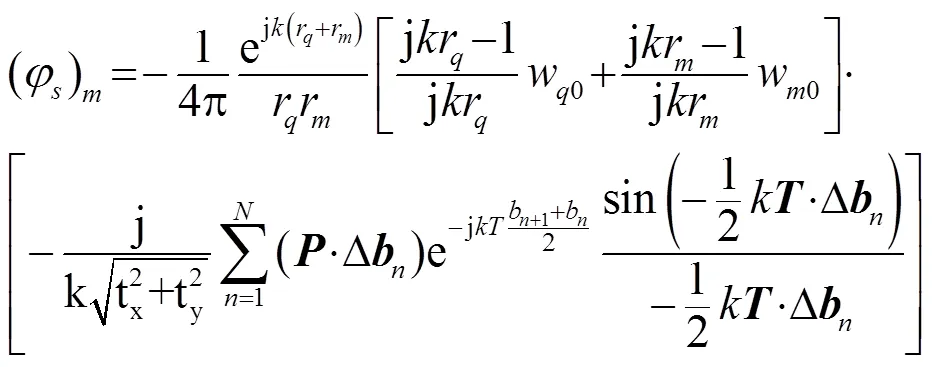
其中,为板块元的边的数目,为第个顶点的位置矢量,且,,,。
声束弹跳法是在板块元法的基础上提出的一种计算多次散射问题的数值计算方法[8]。具体是把入射声波划分为若干声束,根据几何声学理论计算每条声束在目标表面的反射方向和能量损失,经过次反射后,第次反射的声束不与目标表面相交,然后再根据物理声学理论计算产生第次反射声束的目标表面的散射场,将所有声束经过以上计算后的散射场的叠加近似作为整个目标的散射场。声束弹跳法首先需要对目标进行板块元划分,由板块元顶点和声源点确定入射声束;计算产生第次反射声束的目标表面的散射场时,这里的目标表面是重新划分的板块元,需要用到式(5)计算其散射声场。
2 修正声束弹跳方法
声束弹跳法在计算多次散射问题时需要对目标进行多次的板块元划分,即用板块元近似代替曲面面元。对于角反射体目标,其反射面为平面,不存在曲面面元。因此对于角反射体某一反射面的一次散射情况,可直接对平面进行Gordon面元积分计算;对于角反射体各反射面之间的多次散射情况,可由三个反射面和声源点确定三个入射声束,计算声束与反射体相交面的散射声场。由于Gordon面元积分法只能计算反射面边缘为直线情况的散射声场,因此上述方法只能计算反射面边缘为直线的三角形和方形角反射体。这里针对反射面边缘为弧形的圆形角反射体,在声束弹跳法基础上,提出一种对角反射体弧形边缘离散划分的修正声束弹跳法,具体方法如下:
(1) 对组成圆形三面角反射体的弧形边缘(1/4圆弧)进行离散化,即在圆弧上取一些离散点,两点之间的距离取声波波长的1/6或更小,用直线依次连接相邻两点,这样就用一系列相连的线段代替了圆弧,如图1所示。相邻的两个离散点与角反射体顶点(角反射体的三个面相交的点)组成一个三角形面,称之为“一次划分面元”,如图2所示。
(2) 声源点依次与“一次划分面元”的三个顶点相连,连接的三条线为入射声线,三条入射声线组成了入射声束。由三条入射声线计算可得其在“一次划分面元”上的反射声线,即得到“一次反射声束”。同时可用Gordon面元积分法计算得到“一次划分面元”在接收点的散射声场。用镜像法得到声源相对于一次划分面元的“一次反射镜像点”。如图3所示。
(3) 计算“一次反射声束”中通过“一次划分面元”上非角反射体顶点的两个点上的声线与角反射体其它面所在平面的交点。如果没有交点,不计算。当两个交点都在一个平面上时,判断交点与顶点的连线是否小于圆弧半径,当小于或等于圆弧半径时,两交点和角反射体顶点组成的三个点依次相连组成的三角形面称为“二次划分面元”,如图4(a)所示;大于圆弧半径时,两交点分别与角反射体顶点相连的直线与圆弧相交的点,与顶点组成的三个点依次相连组成的三角形面称为“二次划分面元”,如图4(b)所示。当两个交点分别在两个平面上时,同样需要判断交点与顶点的连线是否小于圆弧半径,小于或等于圆弧半径时,计算由“一次反射镜像点”和两个交点组成的平面与两交点所在平面的交线(轴)的交点(称为“轴上交点”),“轴上交点”分别与上面所述平面上的两个交点、以及角反射体顶点一起组成两个三角形面,称为“二次划分面元”,如图5(a)所示;大于圆弧半径时,两个平面上的交点分别与角反射体顶点相连的直线与对应圆弧相交的点,与对应两圆弧连接处的点、以及顶点一起组成两个三角形面,称为“二次划分面元”,如图5(b)所示。
(4) “一次反射镜像点”依次与“二次划分面元”的三个顶点相连,连接的三条线为“一次反射声线”,由三条反射声线计算可得其在“二次划分面元”上的再次反射声线,即得到“二次反射声束”,如图3中所示。把“一次反射镜像点”作为入射声源,利用Gordon面元积分法计算得到“二次划分面元”在接收点的散射声场。同时用镜像法得到“一次反射镜像点”相对于“二次划分面元”的“二次反射镜像点”。
(5) 计算“二次反射声束”中通过“二次划分面元”上非角反射体顶点的两个点上的声线与角反射体其它面所在平面的交点。如果没有交点,不计算。当两个交点都在一个平面上时,判断交点是否小于圆弧半径,小于或等于半径时,两交点和角反射体顶点组成的三个点依次相连组成的三角形面称为“三次划分面元”;大于半径时,两交点分别与角反射体顶点相连的直线与圆弧相交的点,与顶点组成的三个点依次相连组成的三角形面称为“三次划分面元”。当两个交点分别在两个平面上时,同样需要判断交点是否小于圆弧半径,小于或等于半径时,计算由“二次反射镜像点”和两个交点组成的平面与两交点所在平面的交线(轴)的交点(称为“轴上交点”),“轴上交点”分别与上面所述平面上的两个交点、以及角反射体顶点一起组成两个三角形,称为“三次划分面元”;大于半径时,两个平面上的交点分别与角反射体顶点相连的直线与对应圆弧相交的点,与对应两圆弧连接处的点、以及顶点一起组成两个三角形面,称为“三次划分面元”。
(6) 把“二次反射镜像点”作为入射声源,利用Gordon面元积分法计算得到“三次划分面元”在接收点的散射声场。
(7) 把以上计算的散射声场叠加求和,即为一个“一次划分面元”多次散射后的散射声场。
(8) 通过以上步骤,计算角反射体上所有“一次划分面元”多次散射后的散射声场,叠加求和即得到角反射体的总散射声场。
3 计算实例
利用修正声束弹跳法计算了声波频率为800 kHz、圆形角反射体直角边长为0.1 m,刚性边界条件下,收发合置时圆形角反射体在空间不同方位角时的目标强度。在利用修正声束弹跳法计算时,对组成圆形角反射体的弧形边缘进行离散化的两点之间的距离取声波波长的1/6,在利用原始声束弹跳法计算时,对角反射体反射面进行板块元划分的板块元边长也取声波波长的1/6。图6为修正声束弹跳法的计算流程图,图7为计算结果,同时给出了利用原声束弹跳法计算的结果,如图8所示,图9给出了方位角45°时,不同俯仰角时两种方法计算的目标强度值。对比图7、图8以及图9中的计算结果,验证了修正声束弹跳法的正确性。
利用修正声束弹跳法计算时,对组成圆形角反射体的弧形边缘进行离散化,相邻两点与角反射顶点组成一个板块,其与入射声源点组成了一个入射声束,因此我们可以把入射到角反射体上的声波划分为若干声束,角反射体总的散射声场是这些声束的多次散射之后叠加的结果。同样原声束弹跳法利用ANSYS软件进行板块元划分,每一个板块元与入射声源点组成了一个入射声束,总散射场是这些声束的多次散射之后叠加的结果。因此可以比较两种方法所划分的板块数即入射声束数来分析其计算量大小。
以直角边边长为0.1 m的圆形角反射体为例,计算了不同声波频率时两种方法分别划分的入射声束数。其中原声束弹跳法中利用ANSYS软件划分的板块元边长和修正声束弹跳法中弧形边缘进行离散化的相邻两点的距离均为声波波长的1/6。表1为两种方法划分的入射声束数比较结果。由表1可以看出,修正声束弹跳法划分的声束数远小于原声束弹跳法划分的声束数,并且随着频率的增加,声束数减小的程度越大。
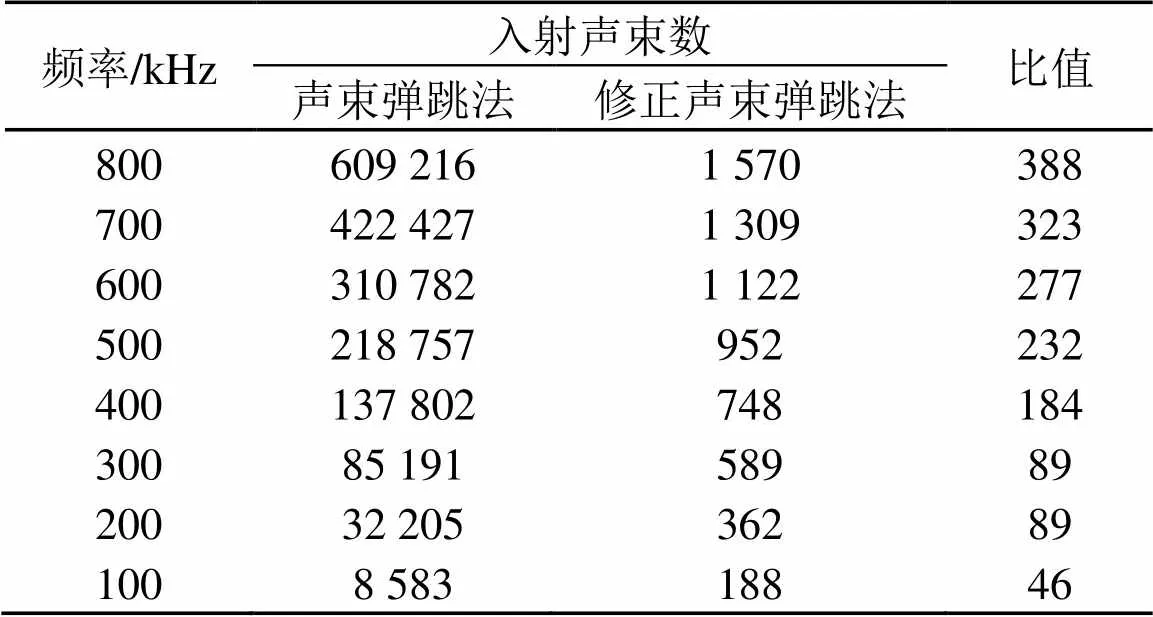
表1 两种方法划分的入射声束数比较
4 结论
针对圆形角反射体的特点,在声束弹跳法基础上提出了一种对角反射体弧形边缘离散划分的修正声束弹跳法。该方法不需要利用计算机辅助软件对角反射体进行建模和板块元划分,其划分的板块是由角反射体顶点和圆弧边缘上的两相邻离散点构成,而非对整个角反射体反射面进行板块元划分,板块数量大大降低。分别采用了原声束弹跳法和修正声束弹跳法计算圆形角反射体散射声场,两种方法计算结果一致,验证了修正之后方法的正确性;两种方法所划分的声束数的比较结果表明,修正声束弹跳法可以减小计算量,并且随着频率的增高,计算量减小的程度越大。
[1] 陈文剑. 水下角反射体声学标记物反向声散射特性研究[D]. 哈尔滨: 哈尔滨工程大学水声工程学院, 2012. CHEN Wenjian. Research on underwater acoustic corner reflector properties[D]. Harbin: College of underwater acoustic engineering, Harbin Engineering University, 2012.
[2] Ling H, Chou R C, Lee S W. Shooting and bouncing rays: calculating the RCS of an arbitrarily shaped cavity[J]. IEEE Transactions on Antennas and Propagation, 2002, 37(2): 194- 205.
[3] 李运周, 史庆藩, 王琪. 高频电磁波多次散射的数值求解[J]. 物理学报, 2006, 55(3): 1119-1125. LI Yunzhou, SHI Qingfan, WANG Qi. Numerical calculation of multiple scattering of high frequency electromagnetic wave[J]. Acta Physica Sinica, 2006, 55(3): 1119-1125.
[4] 王晓冰, 吴振森, 梁子长, 等. 超低空目标与粗糙面复合散射的波束追踪算法[J]. 物理学报, 2012, 61(24): 235-239. WANG Xiaobing, WU Zhensen, LIANG Zichang, et al. Beam- tracking algorithm for composite scattering between low altitude targets and rough surface[J]. Acta Physica Sinica, 2012, 61(24): 235-239.
[5] Tao Y B, Lin H, Bao H J.GPU-Based shooting and bouncing ray method for fast RCS prediction[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(2): 494- 502.
[6] Gao P C, Tao Y B, Lin H. Parallel shooting and bouncing ray method on GPU clusters for analysis of electro- magnetic scattering[J]. Progress in Electromagnetics Research, 2013, 137(1): 87-99.
[7] 郑国垠, 范军, 汤渭霖. 考虑遮挡和二次散射的修正板块元算法[J]. 声学学报, 2011, 36(4): 377-383. ZHENG Guoyin, FAN Jun, TANG Weilin. A modified planar elements method considering occlusion and secondary scattering[J]. Acta Acustica, 2011, 36(4): 377-383.
[8] 陈文剑, 孙辉. 计算水下凹面目标散射声场的声束弹跳法[J]. 声学学报, 2013, 38(2): 147-152. CHEN Wenjian, SUN Hui. A shooting and bouncing beams method for calculating the acoustic scattering field of concave targets[J]. Acta Acustica, 2013, 38(2): 147-152.
[9] 赵维江, 葛德彪. 三面角反射器的高频电磁散射分析[J]. 电波科学学报, 1998, 13(3): 301-303. ZHAO Weijiang, GE Debiao. High-frequency electromagnetic scattering by a square trihedral corner reflector[J]. Chinese Journal of Radio Science, 1998, 13(3): 301-303.
[10] 汤渭霖. 用物理声学方法计算非硬表面的声散射[J]. 声学学报, 1993, 18(1): 45-53. TANG Weilin. Calculation of acoustic scattering of a nonrigid surface using physical acoustic method[J]. Acta Acustica, 1993, 18(1): 45-53.
[11] 范军, 汤渭霖. 声呐目标强度(TS)计算的板块元方法[J]. 声学技术, 1999, 18(增刊): 31-32. FAN Jun, TANG Weilin. The planar element method for computing target strength(TS) of sonar[J]. Technical Acoustics, 1999, 18(Suppl.): 31-32.
[12] 宋君才, 卓琳凯, 范军. 特定形状小目标的回波特性分析[J]. 声学技术, 2010, 29(3): 323-326. SONG Juncai, ZHUO Linkai, FAN Jun. Research on the echo characteristics of small target with special shape[J]. Technical Acoustics, 2010, 29(3): 323-326.
A modified shooting and bouncing beams method for fast calculating the acoustic scattering field of circular trihedral corner reflector
LIANG Jing-jing1, YU Yang2, CHEN Wen-jian2, HU Si-wei2, WANG Hui2, WANG Yi-zhe2
(1.Unit 91918, PLA, Beijing 100230, China; 2. The College of Underwater Acoustic, Harbin Enginnering University, Harbin 150001, Heilongjiang, China)
A modified shooting and bouncing beam method is proposed in this paper, which can calculate the acoustic scattering field of circular trihedral corner reflector quickly. A lot of discrete points are selected on the arc edge of circular trihedral corner reflector. The adjacent two discrete points plus the vertex of corner reflector form a planar element, and the planar element together with the sound source position form an incident sound beam. The reflection of each sound beam is calculated based on geometrical acoustic method; at the same time, the new planar element forms after getting the "radiation" of each sound beam on the reflecting surface. The acoustic scattering field of every planar element is calculated based on physical acoustic method. The superposition of all planar elements’ scattering fields is the corner reflector’s scattering field. The comparison between the results of the original shooting and bouncing beam method and the modified one shows that the two calculations are consistent. However, the modified shooting and bouncing beam method decreases the computational complexity greatly.
circular trihedral corner reflector; multiple scattering; shooting and bouncing beams method; physical acoustic method; geometrical acoustics
TB566
A
1000-3630(2017)-04-0303-06
10.16300/j.cnki.1000-3630.2017.04.002
2016-11-7; 修回时间:2017-02-10
国家自然科学基金青年科学基金项目(11404077)
梁晶晶(1982-), 男, 湖北宜城人, 工程师, 研究方向为通信工程。
陈文剑, E-mail: chwjchwj@163.com

