水声信号动态阈值正交匹配追踪降噪方法

周士贞，曾向阳，王璐



水声信号动态阈值正交匹配追踪降噪方法

周士贞，曾向阳，王璐

(西北工业大学航海学院，陕西西安710072)

为了对实时采集的水声信号进行数据压缩的同时实现信号降噪，提出了一种动态阈值正交匹配追踪方法(Dynamic Threshold Orthogonal Matching Pursuit，DTOMP)。该方法将稀疏分解原理应用于水声信号的预处理，通过在正交匹配追踪算法中引入阈值约束，并根据噪声分布特性将其分为两部分，用以控制预设置的参数。通过对加噪正弦信号、实测鲸鱼叫声和舰船辐射噪声信号的降噪实验，表明该方法能够在对原始水声信号进行压缩的同时提高信噪比，且在较宽的信噪比变化范围内比小波方法具有更好的降噪性能。

降噪；稀疏表示；动态阈值；正交匹配追踪

0 引言

水声信号在采集和传输的过程中受到其他目标、海洋环境干扰以及仪器的影响，导致接收信号不可避免地含有一定的噪声，不利于目标的检测、定位和识别等工作。传统的傅里叶变换可以很好地对稳态信号进行降噪处理，但面对非稳态含噪水声信号时却心有余而力不足。由于水声目标本身的复杂性和海洋信道的多途畸变影响，采用常规的滤波、相关处理等手段，也往往难以实现微弱目标信号的提取。因此，水声信号降噪是一个关键的技术环节。

文献[1]利用统计分析手段对归一化白噪声的经验模态分解结果进行研究，该方法对主要噪声为白噪声的低频水声信号有一定的效果，但当信号频率较高时，去噪效果不明显。文献[2]利用离散子波变换求取相较于传统傅里叶变换方法有更高频率分辨率的功率谱，并通过滑动取值、统计平均的方法保留了稳定信号成分，再配合子波门限实现水声信号去噪。但是该方法可能丢失原始信号相位信息，造成信号恢复上的一些困难。文献[3]通过子波奇异性检测实现水声信号降噪，当选择的信号频谱不完备时，可能造成去噪信号的信息缺失。文献[4]结合小波滤波估计模型和阈值滤波模型对水声信号去噪，但对去噪后小波系数的估计可能会带来误差。总体来看，现有的水声信号降噪方法出发点几乎都是根据噪声和信号分布的差异性，通过寻找信号和噪声的区分域，以某种方式进行筛选。但是筛选方式通常受限于噪声的先验信息。因此，如何基于水声信号的时频分布特性，建立更加有效的噪声与目标信号的分离方法，仍然是值得探索的课题。

文献[5]提出的匹配追踪算法促使稀疏方法在图像、语音、乐音等多个领域得到了广泛的应用，该方法在水声通信、目标定位、声呐图像处理等领域也受到了关注[6-10]。

由于水声信号主要通过振动系统、物理冲击或两者的共同作用产生。其中，共振声信号通常只含少量频率成分，即在频域分布上具有稀疏性；而物理冲击产生的声信号在时域上比较集中，也适用于稀疏分解。文献[11]的研究工作验证了稀疏理论对水声信号进行压缩和重构的可行性。文献[12]将稀疏理论成功用于对水声信道进行估计。本文尝试将稀疏分解原理应用于水声信号降噪，在匹配追踪算法的基础上提出一种新的水声信号降噪方法。通过加入动态阈值控制稀疏分解过程，在减少传输信号数据量的同时能有效提高信噪比。

1 动态阈值正交匹配追踪降噪方法

1.1 水声信号的稀疏分解

水声信号的稀疏分解就是将其映射到稀疏域的过程。稀疏域取决于字典的选择，传统的方法是选用傅里叶变换、小波变换、Gabor变换等已知的变换基来构造稀疏分解字典。在待处理水声信号数据中, 也可以通过利用K-MEANS、K-SVD等算法[13]训练和学习获得相应的字典。

卡洛变换(Karhunent-Loeve Transform，KLT)是最优的信息压缩变换[14]，但其变换性能依赖于待变换数据。离散余弦变换(Discrete Cosine Transform，DCT)作为最接近卡洛变换的正交变换[15]，同时还具有和离散傅里叶变换相似的频率特性和快速算法，因此本文针对水声信号进行稀疏变换时首先考虑离散余弦变换，序列的离散余弦变换为[15]：

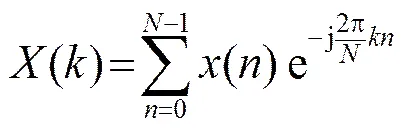
另外，稀疏分解算法的选择也影响信号分解的效率，已有的方法包括匹配追踪算法(Matching Pursuit，MP)[5]、正交匹配追踪算法(Orthogonal Matching Pursuit，OMP)[16]、CoSaMP算法[17]等。

1.2 动态阈值正交匹配追踪降噪方法

本文结合匹配追踪算法[5]的特点，提出基于稀疏分解的水声降噪方法——动态阈值正交匹配追踪降噪方法(DTOMP)。其核心思想是先使用DCT字典实现水声信号的稀疏分解，再根据水声信号中噪声的分布特性，通过设计动态阈值滤除属于噪声的系数，最后重构降噪后的水声信号。算法流程如图1所示。

使用字典矩阵对带噪水声信号进行稀疏表示[8]：

(4)

由于残差是已匹配原子加权求和与信号之差，因此可以通过残差来反映信号中的高斯噪声水平，进而通过控制残差来控制高斯分布对应的阈值。结合每次迭代的残差，可求得：

(6)

另一部分噪声没有确定的数学模型，本文给出一种建模方法，用带噪信号能量减去已选出的确知信号分量，再用控制剩余噪声所占的比例，因此

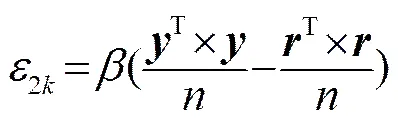
通过阈值筛选后，将该次迭代找到的全部原子索引并入索引集合中，即

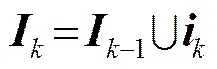
再计算稀疏系数，其元素为：

(9)

(10)

上述迭代过程持续，直至达到最大迭代次数或者残差小于预先设置的残差阈值。最后，经过稀疏重构得到降噪后的信号为[16]：

该算法从一系列残差中选出有用的信号成分，每次迭代匹配出大于阈值的至少一个原子，提高了匹配速度，相比OMP每次选择最匹配的原子的策略，总体计算量有所降低，也不需要额外的空间来存储因式分解结果，解决了OMP算法不适用于大数据量计算的问题。

2 实验分析

为了检验前述降噪算法的性能，使用小波降噪方法进行对比实验[18]。控制变量为门限阈值小波降噪法中的四种阈值规则：无偏似然估计(rigrsure)、启发式阈值(heursure)、固定阈值(sqtwolog)和极值阈值(minimaxi)。采用Matlab自带的wden函数进行降噪，选用具有较好正交对称紧支撑特性的Symlets小波基，小波分解层数和尺度系数均为3，设置小波降噪为软阈值模式，没有重新缩放。

为定量描述降噪效果，定义信噪比为[18]

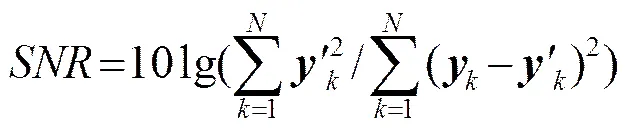
五种方法的降噪效果如图2所示，由图2可以看出，当信噪比较低时小波降噪能起到较好的效果；当原信号信噪比高于某值时，小波降噪后信号信噪比维持在一定的范围内。小波降噪后信噪比曲线和原信号信噪比曲线存在交叉点，说明对于不同信噪比的声信号，小波降噪过程中筛选出的小波系数都相近，该原理导致原信号信噪比较大时，几乎没有降噪效果。经DTOMP算法降噪后的正弦信号，其信噪比曲线处于小波降噪信噪比曲线和原带噪信号信噪比曲线的上方，对每次信号降噪结果求和取平均可以看到，无论何种情况都有一定的降噪效果，明显优于小波降噪方法。

进一步对两类实测水中目标声信号进行降噪，信号波形如图3(a)鲸鱼声信号以及图3(b)舰船噪声信号所示，降噪结果见图4～7所示。与此同时，记录针对鲸鱼声信号的降噪时间见表1。

(a) 鲸鱼声信号

(b) 舰船噪声信号

图3 水中目标(鲸鱼和舰船)声信号

Fig.3 Underwater target (a. whale; b. ship) radiated acoustic signal

表1 DTOMP稀疏降噪和小波降噪两类方法降噪时间对比(s)

(a) 原信号

(b) 带噪信号

(c) DTOMP去噪后信号

(d) 小波去噪后信号

图5 鲸鱼声信号降噪前后波形对比

Fig.5 De-noising consequence of whale acoustic signal

(a) 原信号

(b) 带噪信号

(c) DTOMP去噪后信号

(d) 小波去噪后信号

图7 舰船噪声信号降噪前后波形对比

Fig.7 De-noising consequence of ship noise signal

图4、图6展现了各方法对鲸鱼声信号和舰船噪声降噪后信噪比的变化情况。为更清楚地展现去噪结果，取信噪比为5 dB时的原干净信号波形图、带噪信号波形图、小波降噪后波形以及DTOMP稀疏降噪后波形图进行对比，见图5、图7。通过对比图5、图7可以发现，与正弦信号的结果类似，当信噪比较低时，本文方法和小波降噪方法都具有良好的降噪效果，但随着输入信噪比的增加，采用DTOMP方法得到的输出信号信噪比能稳定提高，且在较低信噪比时，仍有一定的降噪效果，因此具有更宽的作用范围。将本文方法应用于舰船噪声信号时，信噪比改善效果有所下降，分析其原因可能是字典不匹配，导致舰船噪声信号没有被准确地表示，因此稀疏分解的效果逊于同等条件下对鲸鱼声信号和正弦信号的稀疏表示。

由表1可以看出，小波降噪方法依据不同的降噪策略所需的计算时间不同，与本文方法相比，无偏式、固定式、极值式小波降噪方法计算速度更快，而启发式小波降噪稍慢。但总体来看，这几种降噪方法均可满足实际工作需要。

3 结论

本文在正交匹配追踪算法的基础上提出了一种水声信号降噪方法，实验证明该方法能够有效地提高水声信号的信噪比，且输入信噪比越低，提升效果越明显，当输入0 dB信号时，输出信噪比能提高约10 dB，信噪比提升程度依据输入信号类型不同、稀疏表示的准确性而有所差异。相较于小波去噪方法而言，本方法具有更宽的信噪比适用范围，更稳定的降噪效果，因而在水声信号处理中具有一定的应用前景。下一步将针对字典优选和阈值参数学习等问题继续开展研究。总之，将稀疏分解应用于水声信号降噪是一个新的尝试，也是一项有价值的研究课题。

[1] 王剑, 梁斌, 薛飞. 一种基于白噪声EMD分解统计特性的水声信号去噪方法[J]. 四川兵工学报, 2015, 36(6): 131-134. WANG Jian, LIANG Bin, XUE Fei. Method of underwater Acoustic signal de-noising based on characteristics of empirical mode decomposition of white noise[J]. Journal of Sichuan Ordnance, 2015, 36(6): 131-134.

[2] 杨日杰, 何友, 林洪文. 基于子波变换的水声信号去噪方法研究[J]. 系统仿真学报, 2003, 15(7): 1040-1042. YANG Rijie, HE You, LIN Hongwen. The research of underwater acoustic signal de-noising method based on wavelet transform[J]. Journal of System Simulation, 2003, 15(7): 1040-1042.

[3] 杨日杰, 何友, 林洪文. 基于子波奇异性检测的水声信号去噪方法研究[J]. 系统仿真学报, 2003, 15(9): 1328-1330. YANG Rijie, HE You, LIN Hongwen. Research of underwater acoustic signal de-noising method based on singularity detection with wavelet[J]. Journal of System Simulation, 2003, 15(9): 1328- 1330.

[4] 吴光文, 王昌明, 张爱军. 基于小波变换的水声信号滤波方法[J]. 测试技术学报, 2015, 29(4): 299-302. WU Guangwen, WANG Changming, ZHANG Aijun. Underwater acoustic signal de-noising method based on wavelet transform[J]. Journal of Test and Measurement Technology, 2015, 29(4): 299-302.

[5] Mallat S, Zhang Z. Matching Pursuit with Time-frequency Dictionaries[J]. IEEE Trans on Signal Processing, 1993, 41(12): 3397- 3415.

[6] Wang Z, Zhou S, Preisig J C, et al. Per-cluster-prediction based sparse channel estimation for multicarrier underwater acoustic communications signal processing[C]//2011 IEEE International Conference on Communications and Computing (ICSPCC), 2011: 1-6.

[7] Akshaya.B., Narmadha.V., Sree Sharmila.T, et al. Sparse representation to localize objects in underwater acoustic images electrical[C]//2015 IEEE International Conference on Computer and Communication Technologies (ICECCT), 2015, 1-5.

[8] Jinu Joseph, N. Suresh Kumar, Rema Devi M, et al. CS based acoustic source localization and sparse reconstruction using greedy algorithms[C]//2015 Fifth International Conference on Advances in Computing and Communications (ICACC), 2015, 403-407.

[9] Marapulets Y V, Tristanov A B, Lukovenkova O O, et al. The sparse approximation with combined dictionary of the acoustic signals[C]//2014 International Conference on Computer Technologies in Physical and Engineering Applications (ICCTPEA), 2014, 102-103.

[10] Shi C, Nian R, He B, et al. Underwater image sparse representation based on bag-of-words and compressed sensing[C]//OCEANS 2015-MTS/IEEE Washington, 2015, 1-4.

[11] 李佩, 杨益新. 基于压缩感知的水声数据压缩与重构技术[J]. 声学技术, 2014, 33(1): 14-20. LI Pei, YANG Yixin. Compressed sensing based acoustic data compression and reconstruction technology[J]. Technical Acoustics, 2014, 33(1): 14-20.

[12] 伍飞云, 周跃海, 童峰, 等. 可适应稀疏度变化的非均匀范数约束水声信道估计算法[J]. 兵工学报, 2014, 35(9): 1503-1509. WU Feiyun, ZHOU Yuehai, TONG Feng, et al. Non-uniform norm constraint estimation algorithm for underwater acoustic channels at the presence of varying sparsity[J]. Acta Armamentarii, 2014, 35(9): 1503-1509.

[13] Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[14] 周炳. 基于K-L变换的权威页面挖掘的算法[D]. 武汉: 华中科技大学, 2006: 1-2. ZHOU Bing. Authoritative page mining algorithm based on K-L transformation[D]. Wuhan: Hua zhong University of Science and Technology, 2006: 1-2.

[15] Ahmed N, Natarajan T, Rao K R. Discrete cosine transform[J]. IEEE Transactions on Computers, 1974, C-23(1), 90-93.

[16] Pati Y C, Rezaiifar R, Krishnaprasad P S. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition[C]//Proceedings of the 27th Annual Asilomar Conference in Signals, Systems, and Computers. Los Alamitos: IEEE, 1993, 1(11): 40-44.

[17] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301-321.

[18] 钟建军, 宋健, 由长喜, 等. 基于信噪比评价的阈值优选小波降噪法[J]. 清华大学学报(自然科学版), 2014, 54(2): 259-263. ZHONG Jianjun, SONG Jian, YOU Changxi, et al. Wavelet de- noising method with threshold selection rules based on SNR evaluations[J]. J Tsinghua Univ(Sci & Technol), 2014, 54(2): 259-263.

Dynamic threshold orthogonal matching pursuit method for underwater acoustic signal de-noising

ZHOU Shi-zhen, ZENG Xiang-yang, WANG Lu

(School of Marine Science and Technology,Northwestern Polytechnic University,Xi’an710072, Shaanxi,China)

In order to achieve data compression and denoising of realtime collected underwater acoustic signal, this paper presents a dynamic threshold orthogonal matching pursuit (DTOMP) method. This method uses sparse representation for underwater signal pre-processing by applying threshold to greedy algorithm, meanwhile divides noise into two parts according to its characteristics to control preset parameters. Experimental researches on noise reduction of sinusoidal signal plus Gaussian noise, whale blows and ship radiated noise signal indicate that this method could improve the SNR and meanwhile compress original signal. Moreover, this method has better performance over wavelet denoising in wider dynamic range of SNR.

de-noising; sparserepresentation; dynamic threshold; orthogonal matching pursuit

TN911.7

A

1000-3630(2017)-04-0378-05

10.16300/j.cnki.1000-3630.2017.04.014

2016-10-10;

2017-02-21

周士贞(1994－), 女, 湖南衡阳人, 硕士研究生, 研究方向为声信号处理。

周士贞, E-mail: zszltj@163.com