一种基于声压和加速度的矢量水听器定向方法

彭承彦，马树青，熊水东，黄良金，孟洲



一种基于声压和加速度的矢量水听器定向方法

彭承彦，马树青，熊水东，黄良金，孟洲

(国防科学技术大学海洋科学与工程研究院，湖南长沙410073)

根据远场条件下水中声波的加速度和振速方向相同、相位相差π/2的特点，给出了一种加速度型矢量水听器的目标定向方法。基本原理是先计算声压与水平加速度和垂直加速度的互谱，再将互谱的虚部相除，最后求反正切得到目标的方位。相比于常规的复声强器，该方法省略了从加速度转变成振速的积分过程，降低了对滤波器的要求、减少了计算量，具有简单、易于工程实现等优点。光纤矢量水听器的湖上试验数据表明，基于声压和加速度的定向方法与复声强器具有相似的定向性能。

矢量水听器；目标定向；加速度；复声强器

0 引言

近20年来，矢量水听器受到国内外水声界的广泛关注。相比于传统的声压水听器，矢量水听器可以同步共点地测量声场的声压和矢量参数(质点振速、振动加速度和声压梯度等)，为水声信号处理提供了更大的空间和更丰富的内容。同时，矢量水听器的矢量通道具有与频率无关的物理指向性，采用小孔径的传感器即可实现低频弱目标的探测和定向[1]，这些优点使得矢量水听器特别适合于尺度受限载体的声呐系统，具有广阔的军事应用前景[2]。

在利用矢量水听器进行目标定向时，常用的方法有平均声强器、复声强器两种，它们的原理类似，都是利用目标声强在不同矢量通道的投影，通过三角函数关系解算出目标的方位。相比于直接用声场矢量投影的定向方式，声压和质点振速乘积构成的声强器具有相关处理的效果，对噪声的抑制能力更强，在各向同性干扰背景中，声强处理的抗干扰增益为，其中为声信号的时间带宽积，3～4.8 dB为矢量传感器的指向性增益[3]。平均声强器是在时域进行的，它对辐射连续谱噪声的单目标具有很好的效果，但在多目标情况下只能得到合成声强流方向，不能分辨多目标方位；复声强器是在频域进行的，它对接收信号的各个频点做互谱处理，得到各个频率上目标的方位，因此当不同目标辐射噪声的频谱不同时，复声强器便能分别区分这些目标的方位，实现多目标的定向[3]。

根据矢量通道所测的基本物理量不同，矢量水听器可以分为振速型、压力梯度型、位移型和加速度型等，其中加速度型矢量水听器传感的是质点加速度，相应的质点振速可以通过积分运算从加速度间接获得[4]。实际应用中，积分操作可以通过模拟电路(模拟积分)或者可编程器件(数字积分)实现，前者是目前矢量水听器普遍采用的方法。相比于模拟积分，数字积分具有易于实现、灵活性大等优点。此外，对于光纤矢量水听器，其解调出的加速度直接为数字信号，此时只能采用数字积分。理想情况下，积分器的频率响应为双曲线形式()，这意味着信号经过积分器后，低频分量将被大大增强或累积。实际中，低频噪声经过积分器的增强或累积后，会形成很强的干扰，以至于淹没有用的目标信号，因此通常在积分前通过滤波降低低频噪声的影响。然而滤波会增加电路的复杂度或者增大算法的计算量，增加了工程实现的难度。

本文直接从加速度出发，利用声压与加速度的互谱得到目标方位。相比于传统的复声强器，本文提出的方法避开了积分过程，降低了对滤波器的要求，具有简单、易于实现等优点。本文先介绍新方法的原理，并与传统的复声强器进行对比，最后利用光纤矢量水听器的试验数据验证新方法的性能。

1 算法原理

为了简单起见，考虑二维矢量水听器的情况，并假设积分操作由可编程器件实现。

设接收到的声压信号、水平加速度信号和垂直加速度信号分别为

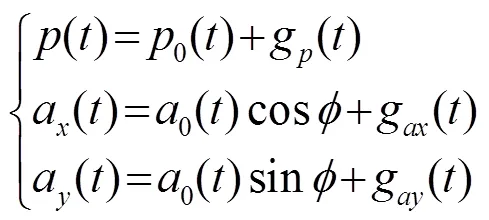
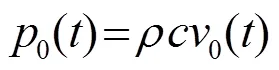
(3)

利用振速与加速度的积分关系，可以得到目标声压与目标加速度的关系满足

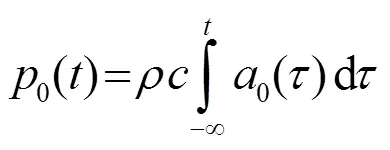
频域形式为

(5)

式(3)和式(5)表明：(1)远场条件下，声压和振速的相位相同，幅度相差一个比例因子，且该比例因子与频率无关，恒等于声阻抗；(2)声压与加速度的相位相差，幅度也成比例关系，但比例因子与频率呈双曲线关系。从式(5)可以看到，加速度的低频分量增强后即得到声压。

1.1 复声强器

为了说明本文方法的优越性，先给出复声强器的定向原理。

于是可以得到水平方位角的估计值为

(7)

式(7)是频率的函数，因此复声强器得到的是一条随频率变化的水平方位曲线。

对于宽带目标，声压和振速在信号频带内是相干的，因此水平方位曲线在信号频带内基本平坦，然而噪声会在该平坦区域引入起伏，影响方位估计的准确性。为了解决这个问题，可以对信号频带内各频点方位角的估计值作统计，得到各个方位角出现的频数，最后将它们的统计平均值作为目标的方位，这种方法称为直方图法[3]，它尽可能多地利用了宽带相干目标的频域信息，对抑制窄带噪声有很好的效果。

对于窄带目标，考虑到信号频率处声压和振速是相关的，并且它们的强度要远高于附近噪声的强度，因此在知道窄带目标频率的前提下，可以直接用该频点处方位角的估计值作为目标的方位。如果接收信号中存在多个窄带目标，只要它们的频率不同，那么可以分别得到它们的方位，从而实现多目标的定向，该方法利用了信号和噪声强度的差异，对宽带噪声中窄带目标的方位估计有较好效果[5]。

实际中，声压信号和加速度信号都会受到环境噪声和自噪声的干扰，造成方位估计的不准确，特别是对加速度通道，平台振动或运动带来的低频噪声是影响其应用的最大问题[6]。这种低频干扰在时域表现为幅度很大的慢变波动，而目标辐射噪声通常是叠加在该波动上强度较小的快变信号。此外，光纤水听器受温度等外界环境的影响，其解调出的相位还将出现低频漂移，形成低频自噪声，进一步影响了目标方位的估计。

考虑了声压和加速度噪声的复声强器框图如图1所示。为了简单起见，图1中省略了对互谱取平均的环节。与前述不同的是，图1中在积分前后分别加入了前滤波和后滤波。由于积分器是一个低通滤波器，低频噪声会在积分过程中被累积，形成幅度很大的低频输出，从而淹没有用信号，因此需要通过前滤波抑制加速度中的低频分量；如果前滤波器的低频衰减不够，则还需通过后滤波进一步降低低频噪声的影响，极端情况下，还需要在前滤波中加入去除直流和线性趋势项的操作(图1中未画出)。

前滤波和后滤波会引入额外的计算量，一般这些计算量是相当可观的，例如当采用有限冲激响应(Finite Impulse Response，FIR)滤波器时，为了获得较大的带外衰减，前后滤波器的阶次需要上百阶，相应的计算量通常为FFT的数十倍，这对许多实时系统提出了更高的要求。一方面系统的计算能力要足够强，以满足滤波、积分和FFT等操作的需要，另一方面，额外的计算要消耗更多的功耗，缩短了自主系统的工作时间，而更多的算法步骤也增加了工程实现的复杂性。

除了计算量增大外，在实际应用中，还需要考虑前后滤波器截止频率、阶次的选择问题，通常最佳滤波器是由信号和噪声的统计特性决定的，但一般情况下，无法获得这些信息，因此需要根据方位估计效果不断调整滤波器的参数，这在实时系统中也是不允许的。

1.2 基于声压和加速度的定向

从式(4)中可以看到，加速度转变成振速的积分运算是对时间变量进行的，在这个过程中目标方位没有发生改变，即加速度信号和振速信号包含的方位信息是相同的，它们的数学表达式也相同；从物理概念上理解，这是因为远场情况下，水中声波的加速度与振速具有相同的方向，因此可以直接从加速度出发，利用互谱处理得到目标的方位。

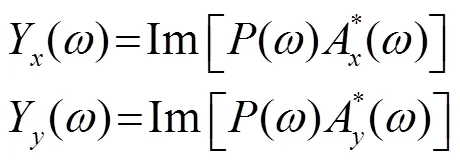
类似地，水平方位角的估计式可以写为

(9)

对比式(7)和式(9)可以发现，基于加速度和基于复声强的目标定向算法具有相同的数学表达式，计算过程也基本相同，只需将图1中虚线框内的步骤去掉，并且将取实部改为取虚部即可。此外，易知对复声强适用的直方图法和窄带处理同样适用于基于声压和加速度的定向方法。由于加速度和振速具有相同的偶极子指向性，因此在各向同性噪声背景下，基于声压和加速度的互谱处理和复声强器有相同的空间处理增益。然而，基于声压和加速度的处理方法无需将加速度转换成振速，避免了低频噪声在积分过程中的累积、进而淹没有用信号的问题；并且无需前后滤波，节省了大量的计算资源，易于工程实现。实际中，为了减小大幅度低频噪声分量的频谱泄漏对信号频段的影响，仍需适当地滤除低频噪声，然而这种情况下对滤波器的要求已经降低了。

2 湖试结果

通过湖上试验数据验证基于声压和加速度的目标定向算法的有效性。

将光纤矢量水听器布放于水下30m处，并使渔船以100m的半径绕着水听器转圈，水听器接收渔船的辐射噪声。图2中蓝线给出了声压和水平加速度的时域波形图(垂直加速度的波形与水平加速度的波形类似，此处未给出)，其中采样率为8 000Hz，信号总长度约250 s。图中还给出了信号的慢变趋势，如红线所示，它们分别对应声压通道和加速度通道的低频成份，而需要的渔船辐射噪声则叠加于该低频波动上，是快变分量。图3给出了声压信号和水平加速度信号的时频图，从图中可以看到，光纤水听器的输出具有较强的低频噪声，特别是对于加速度通道。对加速度的谱分析表明，30 Hz以内线谱信号的强度比100 Hz以上连续谱的强度高50 dB左右。

图4给出了两种方法的方位历程图，处理条件为：复声强器的前后滤波器均为256阶的高通滤波器，截止频率为100Hz，基于声压和加速度的定向采用相同的前滤波器，FFT长度都为8 000点，对每个FFT结果利用直方图法进行方位估计，统计频段为100～3000Hz。从图4可以看到，两种方法得到的结果几乎相同，对其他湖试数据，也得到了类似的结果，因此基于声压和加速度的定向方法与复声强器的效果相当，但是省略了一个滤波器和积分操作，更加简单直接。

(a)声压信号

(b)水平加速度信号

图2 光纤矢量水听器的声压和水平加速度(通道)的时域波形

Fig.2 Time domain waveforms of pressure and horizontal acceleration for optical fiber vector hydrophone

(a)声压信号

(b)水平加速度信号

图3 光纤矢量水听器的声压和水平加速度(通道)的时频图

Fig.3 Time-frequency distributions of pressure and horizontal acceleration for optical fiber vector hydrophone

(a)声压和加速度方法

(b)复声强器方法

图4 基于声压-加速度方法的方位历程图和复声强器的方位历程图

Fig.4 Orientation course maps of the pressure-acceleration based method and the complex intensity processor

3 结论

实际应用中，受低频自噪声和环境噪声的影响，复声强器的积分输出会出现幅度很大的低频分量，淹没了有用信号，影响了复声强的定向性能。多级滤波是解决该问题的一个方法，但是却存在计算量大、滤波参数难以确定等问题，增加了工程实现的难度。本文根据水中声波加速度与振速方向相同的特点，直接利用声压和加速度的互谱，实现了目标的定向，光纤水听器的湖上试验数据也验证了该方法的有效性。本文提出的定向方法避开了积分环节，降低了计算量，更加简单直接，有望成为工程应用中更合适的一种定向方法。

[1] 陈晓昭, 陈建峰, 王绪虎, 等.矢量水听器工程局限性剖析[J]. 声学技术, 2012, 31(5):490-496. CHEN Xiaozhao, CHEN Jianfeng, WANG Xuhu, et al. Limitations of acoustic vector sensor in engineering application[J]. Technical Acoustics, 2012, 31(5):490-496.

[2] 吴艳群, 胡永明. Pekeris波导中矢量水听器定向性能分析[J]. 兵工学报, 2009, 30(11):1484-1487. WU Yanqun, HU Yongming. Directional performance of acoustic vector sensors in Pekeris waveguide[J]. Acta Armamentarii, 2009, 30(11):1484-1487.

[3] 惠俊英. 矢量声信号处理基础[M]. 北京: 国防工业出版社, 2009. HUI Junying. Fundamentals of vector acoustic signal processing [M]. Beijing: National Defense Industry Press, 2009.

[4] 朱良明. 基于矢量水听器的浅海矢量声场特性及其应用研究[D]. 北京:中国科学院大学, 2015. ZHU Liangming. Research on properties and applications of vector acoustic field in shallow water by vector hydrophone[D]. Beijing: University of Chinese Academy of Sciences, 2015.

[5] 姚直象. 单矢量水听器信号处理研究[D]. 哈尔滨: 哈尔滨工程大学, 2005. YAO Zhixiang. Signal processing for single vector acoustic sensor [D]. Harbin:Harbin Engineering University, 2005.

[6] D’Spain G L, Luby J C, Wilson G R, et al. Vector sensors and vector sensor line arrays: Comments on optimal array gain and detection[J]. J. Acoust. Soc. Am., 2006, 120(120):171-185.

A pressure-acceleration based orientation method for vector hydrophone

PENGCheng-yan, MAShu-qing, XIONGShui-dong, HUANGLiang-jin, MENGZhou

(Marine Science and Engineering Research Institute,National University of Defense Technology,Changsha410073,Hu’nan,China)

Based on the fact that the acceleration and velocity of underwater acoustic wave in far field has the same direction and aπ/2 phase difference, this paper proposes a target orientation method for acceleration type vector hydrophone. The basic principle is: first to calculate the cross-spectrum between pressure and horizontal acceleration as well as the cross-spectrum between pressure and vertical acceleration; then to divide the imaginary part of the first cross-spectrum by the imaginary part of the next one, and finally to find the target direction by taking the arctangent of the quotient. Compared to conventional complex intensity processor, the new method is simple and easy to implement since the integration from acceleration to velocity is no longer needed, which reduces the requirement of filtering. Lake experiment data of optical fiber vector hydrophone show that the new method has similar orientation performance in comparison with the complex intensity processor.

acoustic vector sensor; target orientation;acceleration; complex intensity processor

TN911.7

A

1000-3630(2017)-04-0394-05

10.16300/j.cnki.1000-3630.2017.04.017

2016-10-20;

2017-03-09

863项目(2013AA09A412-1)、国防科学技术大学重大应用基础研究项目(ZDYYJCYJ20140701)资助

彭承彦(1987－), 男, 湖南长沙人, 博士研究生, 助理研究员,研究方向为水声信号处理。

马树青, E-mail: mashuqing@nudt.edu.cn