基于部分散射系数矩阵的缺陷识别方法研究

周进节，郑阳，张宗健，谭继东



基于部分散射系数矩阵的缺陷识别方法研究

周进节1，郑阳2，张宗健2，谭继东2

(1. 中北大学机械与动力工程学院，山西太原030051；2.中国特种设备检测研究院国家质量监督检验检疫总局无损检测与评价重点实验室，北京100029)

为了在相控阵超声成像检测时实现缺陷的定性分析，采用部分散射系数矩阵表征传感器采集到的部分散射场信息，并利用部分散射系数矩阵图进行缺陷识别。以相控阵超声全阵列采集获取到的全矩阵数据为基础，结合声波传播过程的衰减性，采用逆向补偿的方法将全矩阵数据补偿到以缺陷为中心的同一圆周上，以此获取缺陷的部分散射信息，并采用部分散射系数矩阵来表征。通过分析缺陷的部分散射系数矩阵图特征，对缺陷进行定性分析和判别。采用此方法对两种典型的缺陷进行仿真实验，结果显示，部分散射系数矩阵图不仅对圆孔和裂纹两类不同缺陷表现出差异性，对同类型不同尺寸和不同角度的裂纹也有明显的不同之处，表明利用该方法可实现缺陷的定性识别。

超声；散射；散射系数矩阵；缺陷识别；相控阵

0 引言

相控阵超声通过对阵元晶片设置一定的激励法则，可实现声束的偏转和聚焦，在缺陷检测中因其具有分辨率高、扫查方式灵活、形象直观等特点而得到广泛应用[1-4]。随着硬件技术和成像后处理技术的发展，相控阵超声在成像精度上得到了极大提高，但目前仍然不能实现对缺陷的准确定性定量分析。为此，近年来国内外很多学者致力于研究相控阵超声检测缺陷的定性定量分析方法。Zhang J等采用相控阵超声测量缺陷处的散射矩阵，并用此表征缺陷特征[5]，随后其又采用散射矩阵和全聚焦成像两种不同方法对裂纹类缺陷进行定性定量分析，表明两种方法均可获取到裂纹的长度和方向信息，但信噪比是影响测量结果的关键[6]。Wilcox[7]等人利用矢量全聚焦方法对相控阵采集到的全矩阵数据进行处理，通过裂纹缺陷的矢量场方向确定其方向。焦敬品[8]等人也进行了类似的研究，从相控阵子阵列中提取散射系数进行裂纹方向识别，并研究了子阵列参数及探头位置对裂纹方向识别的影响。Bai L[9]等人采用相关系数和结构相似性指数作为散射矩阵定性缺陷的指标，研究了在两种不同噪声水平下散射矩阵对小裂纹缺陷的定性分析。

纵观对缺陷定性定量方法的研究，多是在已知缺陷类型的情况下，判断缺陷的方向和测量缺陷的大小，而在实际检测中缺陷的类型是未知的。在未知缺陷的情况下，分析识别缺陷的类型对实际检测具有重要意义，特别是对裂纹类缺陷的识别。本文以相控阵超声检测全矩阵数据为基础，提出了基于部分散射系数矩阵的缺陷识别方法，并对比研究了不同类型缺陷的定性分析效果。

1 基于部分散射系数矩阵的缺陷识别方法

1.1 全矩阵数据

全矩阵数据是在相控阵超声检测时，通过全矩阵采集(Full Matrix Capture，FMC)的数据获取方式得到的，记录了传感器阵元所有的激励-接收组合信号。FMC是指单次激励相控阵换能器的一个阵元晶片，利用所有阵元来接收信号，按照此方式顺次激励所有阵元并完成信号采集，便可获得相控阵超声传感器所有阵元发射-接收组合的信号，即全矩阵数据。全矩阵数据包含了所有激励阵元和接收阵元的信息。

如图1所示，以具有个阵元的相控阵超声传感器为例，展示FMC的具体过程：单独激励一个阵元，然后设置所有阵元全部接收，便可获取到一组发射-接收组合信号，其中=1,2,…,，代表激励阵元，=1,2,…,，代表接收阵元。依次激励所有阵元，便可获得×组检测信号数据。

按照矩阵的形式组织所有的相控阵超声检测信号P，便形成了全矩阵数据，元素P记录的是时间幅值信息，的表达方式为

式中，下角表示激励，表示接收。

1.2 部分散射系数矩阵提取

超声与缺陷交互作用后会形成新的散射场分布，为了描述超声在缺陷处的散射特性，常采用散射系数矩阵(矩阵)来表达。矩阵描述了远场散射位移场幅值与入射角、散射角的关系，同时矩阵还是频率、入射及散射模态的函数，可表达为。矩阵的物理意义为模态超声波以角度θ入射到缺陷处时，在角度上散射的模态的权重系数，实际检测中常采用散射位移场和入射位移场来表示散射矩阵，求解方法如下：

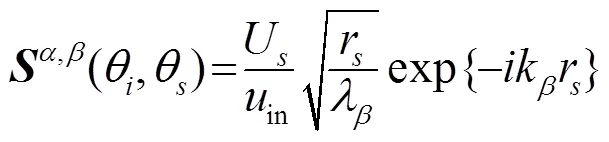
其中：上标和表示入射及散射模态；为散射位移场；in为入射位移场；为散射信号采集点到缺陷的距离；λ为散射模态的波长；为散射模态的波数。

由于相控阵超声传感器的尺寸和阵元数有限，检测时传感器只能接收到缺陷处散射的部分信号。检测过程中采用FMC方式进行信号采集，得到的全矩阵数据可最大限度地包含缺陷的散射信息，且从全矩阵数据中可提取出部分散射系数矩阵，具体的提取方法如下：

相控阵超声换能器的晶元排布形式有多种，在此只讨论一维线阵探头检测缺陷时的情况，如图2所示。为了提取到纯净的散射信号，采用缺陷信号减去没有缺陷的参考号信来获取散射信号，并采用部分散射系数矩阵来记录从全矩阵数据中提取到的散射信息。部分散射系数矩阵记录了相控阵入射声场、入射角以及散射角，还包含了入射波和散射波的模态信息，可表示为，其中代表入射模态；是声波散射模态；为入射角；是散射角；为入射波的角频率。对于相控阵超声而言，和取纵波L或横波S。

定义如图2所示的角度坐标系，为了便于计算，固定传感器位置不变，对于同一激励阵元而言，通过改变缺陷角度达到阵元声波从不同角度入射到缺陷时的效果，在计算散射矩阵时通过角度变换，把缺陷角变换为相应的声波入射角即可。

此外，由于一维线阵探头的晶元排布方式为直线排布，各阵元采集到的信号并不在以缺陷为中心的同一信号圆上，因此从全矩阵数据中提取缺陷散射信息时，需要把各通道的信号进行衰减补偿，转换到同一信号圆上。相控阵超声入射到缺陷后将会形成新的声场分布，相当于把缺陷看作新的声源，在忽略传播介质对声波衰减的情况下，声波能量将按衰减[10]，其中表示声程，据此把从全矩阵数据中提取出散射系数逆向补偿到同一信号圆上，得到缺陷的部分散射系数矩阵。把部分散射系数矩阵绘制成图谱，用于缺陷定性识别分析。

2 典型缺陷识别的仿真实验

2.1 建立仿真模型

为了获取到相控阵超声检测的全矩阵数据，建立相控阵传感器检测缺陷的二维有限元模型，仿真全矩阵采集(FMC)过程，如图3所示。考虑在实际检测中，总可以移动探头使缺陷位于传感器的正下方，因此在传感器的正下方设置缺陷。

其中传感器选择阵元数为=32、激活孔径为19.2 mm、阵元中心间距为0.6 mm的一维线阵相控阵传感器。为了便于提取缺陷的部分散射信息，采用阻尼层法在模型边界处设置一总层数为25层、单层宽度0.2 mm、总宽5 mm的吸收边界，用于吸收边界回波，其中阻尼层与被检材料相同，只增加了Rayleigh阻尼系数，且阻尼系数值从里到外逐层呈指数递增[11]。相关仿真参数如表1所示。

表1 有限元仿真参数表

2.2 圆孔缺陷的部分散射系数矩阵

在模型中设置不同大小的系列圆孔缺陷，直径分别取0.5、1、1.5和2，其中为纵波波长，通过仿真获取它们的全矩阵数据，并利用1.2节中所述方法提取圆孔的L-L模态部分散射系数矩阵，并绘制为散射矩阵图，如图4所示。图中横坐标为相控阵超声入射角度，纵坐标为散射角度，色彩颜色值代表散射能量幅值。部分散射系数矩阵图中，入射角为相控阵各阵元激励超声入射到缺陷时的角度；散射角表示相控阵超声传感器所有阵元能接收到散射场信号所对应的角度。

(a) 圆孔直径为0.5(b) 圆孔直径为1

(c) 圆孔直径为1.5(d) 圆孔直径为2

图4 不同直径圆孔缺陷的部分散射系数矩阵图

Fig.4 Partial scattering coefficient matrices of the holes with different diameters

图4中相控阵各阵元激励超声入射到圆孔的入射角范围在70°～110°内，传感器接收到的散射场信号对应角度在70°～110°内。部分散射系数矩阵图中包含了阵元激励的超声以一定角度范围入射至圆孔时，传感器能接收到的所有部分散射信息。从图中任取一入射角，其对应的纵轴散射信息代表了该入射角下传感器接收到的圆孔散射场的部分信息。分析图4可以看出：对于圆孔缺陷，提取到的部分散射能量主要集中在散射系数矩阵的副对角线上；整体分布趋势沿副对角线方向，有明显的方向性；随着圆孔直径的增加，脊区(能量明显高于周围的区域)在变长变宽，散射的能量在增加。

2.3 裂纹缺陷的部分散射信息

在模型中设计椭圆表征的裂纹缺陷，椭圆的短轴长固定为0.2 mm，长轴分别为0.5、1、1.5和2，为超声纵波波长。通过仿真获取不同长度裂纹的全矩阵数据，提取L-L模态部分散射系数矩阵。

如图5所示，绘制了裂纹角度为0°时不同长度裂纹的部分散射系数矩阵图，图中相控阵各阵元激励的超声入射到裂纹的入射角范围在70°～110°内，传感器接收到的散射场信号对应角度在70°～110°内。从图中任取一入射角，其对应的纵轴散射信息代表了该入射角下传感器接收到的裂纹散射场的部分信息。分析图5可以直观地看出：在裂纹长度为0.5时，散射系数矩阵图能量主要集中在中心区域，没有明显的方向性，但是当裂纹长度增加后，可以看出散射能量集中在主对角线上及周围区域，表现出明显的方向性；裂纹缺陷的部分散射系数矩阵图有唯一的脊区，其外形为椭圆形并且随着裂纹长度的增加，脊区变窄变长。

(a) 裂纹长度为0.5(b) 裂纹长度为1

(c) 裂纹长度为1.5(d) 裂纹长度为2

图5 不同长度裂纹的部分散射系数矩阵图

Fig.5 Partial scattering coefficient matrices of different length cracks

为了分析不同角度裂纹的部分散射系数矩阵的区别与联系，对同一长度的裂纹在90°范围内等间隔设置5个裂纹角度，仿真获取不同角度下裂纹缺陷的全矩阵数据，并提取部分散射系数矩阵。图6是长度为2的裂纹在不同缺陷角度下的部分散射系数矩阵图。

(a) 裂纹角度为22.5°    (b) 裂纹角度为45°

(c) 裂纹角度为67.5°    (d) 裂纹角度为90°

图6 不同角度裂纹的部分散射矩阵图

Fig.6 Partial scattering coefficient matrix of the crack at different angles

结合图6和图5 (d)，可以直观地看出，不同角度下裂纹的部分散射系数矩阵图形态不同。裂纹角度为0°时部分散射系数矩阵图有唯一的脊区，其外形为椭圆，主要分布在主对角线上，随着角度的增加，散射矩阵图的脊区向右上角移动，呈三角状且逐渐变小，如图6(a)和6(b)所示。裂纹角度进一步增大，脊区开始转移到副对角线上，呈现状区域且随着角度增大自右上角向左下角延伸，如图6(c)和6(d)所示。

对比分析图4和图5可看出，当缺陷的长度或直径大于0.5时，圆孔缺陷和裂纹缺陷在部分散射系数矩阵图的形态上有明显的差异，主要表现为脊区的分布形态和朝向不同。裂纹的脊区外形轮廓为椭圆形，朝向为主对角线方向，分布范围随裂纹长度增加而减小；而圆孔的脊区外形不规则，朝向为副对角线方向，分布范围随圆孔直径增加而增大，且中心脊区能力增强。因此，可以通过分析部分散射系数矩阵图的分布、形态和朝向来分辨圆孔大小和裂纹长度。此外，对比分析图5和图6可发现，部分散射系数矩阵中包含有裂纹的大小、方向等特征信息，可以采用矩阵图谱辅助分析和识别位于探头正下方裂纹的大小和方向。

3 结论

本文采用部分散射系数矩阵表征传感器采集到的部分散射场信息，并利用部分散射系数矩阵图进行缺陷识别。通过仿真研究了该方法对典型的圆孔缺陷和裂纹缺陷的识别效果，得出以下结论：

(1) 当缺陷的长度或直径大于0.5且裂纹方向为0°时，圆孔缺陷和裂纹缺陷在部分散射系数矩阵图的形态上有明显的差异，可以通过分析部分散射系数矩阵图脊区的分布形态和朝向来分辨圆孔和裂纹。

(2) 部分散射系数矩阵中包含有裂纹的大小、方向等特征信息，可以采用矩阵图谱辅助分析和识别位于探头正下方裂纹的大小和方向。

[1] 施克仁, 郭寓岷, 霍健, 等. 相控阵超声成像检测[M]. 北京: 高等教育出版社, 2010: 31-47. SHI Keren, GUO Yumin, HUO Jian, et al. Phased array utrasonic imaging and testing[M]. Beijing: Higher Education Press, 2010: 31-47.

[2] Gueudre C, Marrec L L, Moysan J, et al. Direct model optimisation for data inversion. Application to ultrasonic characterisation of heterogeneous welds[J]. NDT & E International, 2009, 42(1): 47-55.

[3] GUAN X, ZHANG J, RASSELKORDE E M, et al. Material damage diagnosis and characterization for turbine rotors using three-dimensional adaptive ultrasonic NDE data reconstruction techniques[J]. Ultrasonics, 2014, 54(2): 516-525.

[4] SONG S J, SHIN H J, JANG Y H. Development of an ultrasonic phased array system for nondestructive tests of nuclear power plant components[J]. Nuclear Engineering and Design, 2002, 214(1): 151-161.

[5] ZHANG J, DRINKWATER B W, WILCOX P D. Defect characterization using an ultrasonic array to measure the scattering coefficient matrix[J]. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on, 2008, 55(10): 2254-2265.

[6] ZHANG J, DRINKWATER B W, WILCOX P D. The use of ultrasonic arrays to characterize crack-like defects[J]. Journal of Nondestructive Evaluation, 2010, 29(4): 222-232.

[7] WILCOX P D, HOLMES C, DRINKWATER B W. Advanced reflector characterization with ultrasonic phased arrays in NDE applications[J]. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on, 2007, 54(8): 1541-1550.

[8] 焦敬品, 马婷, 李光海, 等. 用于裂纹方向识别的超声散射系数分析方法研究[J]. 声学学报, 2016, 41(1): 13-24. JIAO Jingpin, MA Ting, LI Guanghai, et al. Characterization of the directivity of crack-like defects based on the distribution of scattering coefficient and its influencing parameters[J]. Acta Acustica, 2016, 41(1): 13-24.

[9] BAI L, VELICHKO A, DRINKWATER B W. Ultrasonic characterization of crack-like defects using scattering matrix similarity metrics[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2015, 62(3): 545-559.

[10] 郑阳. 基于散射系数矩阵法的超声兰姆波与典型缺陷交互作用研究[D]. 北京：北京工业大学, 2012. ZHENG Yang. Interaction of lamb wave with typical defects using scattering parameter matrix[D]. Beijing: Beijing University of Technology, 2012.

[11] 吴斌, 张也弛, 郑阳, 等. 超声导波有限元仿真中吸收边界设置及参数[J]. 北京工业大学学报, 2013, 39(12): 1777-1783. WU Bin, ZHANG Yechi, ZHENG Yang, et al. Modeling and parameters of absorbing boundary for ultrasonic-guided wave in fe simulation[J]. Journal of Beijing University of Technology, 2013, 39(12): 1777-1783.

Research on defect recognition method based on partial scattering coefficient matrix

ZHOU Jin-jie1, ZHENG Yang2, ZHANG Zong-jian2, TAN Ji-dong2

(1. School of Mechanical and Power Engineering, North University of China, Taiyuan 030051,Shanxi,China；2. China Special Equipment Inspection and Research Institute, Key Laboratory of Nondestructive Testing and Evaluation of General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Beijing 100029, China)

In order to realize the qualitative analysis of defects in ultrasonic imaging of phased array, partial scattering coefficient matrix is used to characterize the partial scattering field information collected by the sensor, and the defect identification is performed by the partial scattering coefficient matrix chart. Based on the full matrix data acquired by full matrix capture of phased array ultrasound and combined with acoustic attenuation of the propagation process, the partial scattering information of defects is obtained by using the inverse compensation method to compensate the fullmatrix data to the same circle with the defect asthe center, and the partial scattering coefficient matrix is used to represent the partial scattering information. By analyzing the characteristics of the partial scattering coefficient matrix graph of the defect, the defect can be qualitatively analyzed and distinguished. Simulation experiment is carried out by using this method for two typical defects, and results show that obvious differences not only exist in the partial scattering coefficient matrices of both hole and crack defects, but also exist in cracks with different sizes and different angles. It is therefore proven that the method can realize the qualitative identification of defects.

ultrasonic; scattering; scattering coefficient matrix; defect recognition; phased array

TB553 TG115.28+5

A

1000-3630(2017)-04-0335-05

10.16300/j.cnki.1000-3630.2017.04.007

2016-08-08;

2016-11-10

质检公益性行业科研专项(201410026、201510068)、质检总局科技计划项目(2014QK252)资助

周进节(1981－), 男, 湖北天门人, 博士, 讲师, 研究方向为超声无损检测与评价、传感器与检测仪器开发、自动化检测系统研究等。

郑阳, E-mail: zhengyangchina@126.com