开圆洞钢板剪力墙的承载力与耗能性能研究

刘佳伟，李启才

（苏州科技大学 土木工程学院，江苏 苏州215011）

开圆洞钢板剪力墙的承载力与耗能性能研究

刘佳伟，李启才

（苏州科技大学 土木工程学院，江苏 苏州215011）

对开圆洞钢板剪力墙进行改进，提出了一种新型的侧边带有竖向加劲但不与柱连接的开圆洞钢板剪力墙。通过分析其受力机理，假设钢板出现塑性铰的区域并推导了新型开圆洞钢板剪力墙的弹性初始刚度和极限承载力理论计算公式。采用ABAQUS有限元软件对钢板剪力墙进行数值模拟分析，采用新的初始缺陷考虑方法，研究开圆洞钢板剪力墙的受力性能并验证理论公式的正确性。结果表明，开圆洞钢板剪力墙的塑性铰位置假设正确；理论公式与有限元模拟结果符合；开圆洞钢板剪力墙在后期进入弹塑性阶段的耗能性能良好。

开圆洞钢板剪力墙；弹性初始刚度；极限承载力；耗能性能

钢板剪力墙的内嵌钢板一般使用薄钢板，利用其屈曲后形成的拉力带作用继续抵抗层间剪力，利用沿着拉力场方向屈服来耗散地震能量[1-2]。但是薄钢板可能因大风作用而提前发生屈曲，屈曲后的平面外变形可能会相对较大，甚至会大于其平面内侧移，使钢板剪力墙因平面外凸曲过大并产生不必要的噪音而引起居住者的恐慌。开圆洞钢板剪力墙[3]是通过在内嵌钢板上有规律地交错开圆孔来减弱拉力带作用并减小钢板屈曲时产生的面外变形（见图1），从而增强钢板的变形能力，它是钢板剪力墙的一种改进形式，在地震作用下作为主要的抗侧力构件和耗能器，能够先于主体结构发生塑性破坏，通过塑性变形来耗散地震输入的能量。

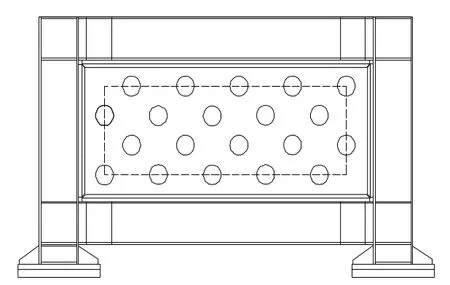
图1 开圆洞钢板剪力墙示意图

传统钢板剪力墙结构的拉力带作用十分强，框架柱很容易先于整体结构发生破坏。为了避免内嵌薄钢板拉力场对柱子的不利影响，出现了内嵌钢板不与柱连接的钢板剪力墙[4-5]。新型的改进开圆洞钢板剪力墙的内嵌钢板开有圆洞，且钢板只与框架梁连接，两侧边用冷弯槽钢加劲以增强内嵌钢板的抗侧刚度，如图2所示，这样能够更好地实现“强框架、弱钢板”的设计理念。

图2 新型开圆洞钢板剪力墙示意图

文中将通过分析开圆洞钢板剪力墙的受力机理来提出其刚度和承载力理论计算公式，然后对不同几何尺寸开圆洞钢板剪力墙进行ABAQUS有限元模拟分析，最后通过对模拟得到的数值与理论公式计算值进行对比分析，从而验证其是否正确。

1 开圆洞钢板剪力墙的理论分析

1.1 圆洞的受力分析

开圆洞钢板剪力墙会因圆孔的存在而使其拉力场作用减弱，原因在于钢板开圆洞打断了钢板拉力带的传力路径[6]，如图3所示，会使得应力重新分布。

开圆洞钢板剪力墙能通过使圆环变形为椭圆环来减轻钢板的面外屈曲。图4（a）为开圆洞钢板剪力墙拉力带上圆孔在拉应力下变形分析，图4（b）为未开圆洞钢板剪力墙的拉力带上应力单元在拉应力下变形分析。图4（a）中圆的周长为Pcircle，圆孔半径为r，椭圆的周长Pellipse；图4中的δ1为沿拉力带纵向的伸长量；δ2为沿拉力带横向的缩短量。文献[7]推出圆孔的纵向伸长量δ1和横向收缩量δ2的关系见公式（1）～（2）。假设圆的周长与椭圆的周长相等，则可推出公式（3）。图5是文献[7]给出的圆孔和正方形的纵向伸长量δ1与横向收缩量δ2关系曲线，下面的直线代表了未开洞钢板的δ1与δ2关系曲线，上面的曲线代表了开圆洞钢板的δ1与δ2关系曲线。在弹性区范围，δ1=0.28δ2（0.28为材料的泊松比），而开圆洞钢板的材料泊松比数值增加到 0.5。假设公式（3）中的圆孔半径 r=200mm 或者 400mm 时，令 δ1=5mm，按公式（3）可求得 δ2，发现 δ1与 δ2近似相等，并由图5中圆的δ1与δ2关系曲线可知，圆孔压力带的缩短量与拉力带的伸长量绝对值相差更小，这就极大缓解了压力方向的面外失稳并减轻了平面外屈曲。圆的这种独特的变形方式使得开圆洞的钢板剪力墙与非加劲的薄钢板相比，具有更好的面内刚度，滞回曲线也变得更为饱满。

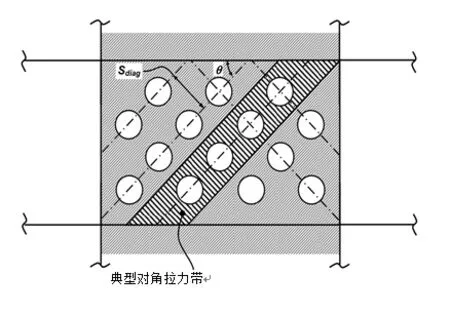
图3 开圆洞钢板剪力墙拉力带示意图

图4 变形图

图5 δ1与 δ2关系曲线

图6为文献[3]运用ABAQUS有限元软件对开圆洞钢板剪力墙拟静力位移加载结果的应力云图，从图6可以发现，应力最大值主要集中在沿对角线方向的圆孔边缘，在拉压应力转换的情况下，圆孔的两个方向的对角线交点最容易发生应力集中从而截面屈服并形成塑性铰，最终发生撕裂破坏。从文献[8]中拉力带的平面内最大主应力和应变云图分析（见图7）可知，应力应变的最大值集中在圆孔边缘并沿45°的方向向外辐射。研究发现，开圆洞钢板剪力墙在一些情况下能够减少钢板发生屈曲的范围并发现潜在的两种屈曲模式，其中一种是类似于实心钢板的拉力带屈曲的整体剪切屈曲，另一种则是圆孔的侧向扭转屈曲。

图6 开圆洞钢板剪力墙拟静力位移加载的应力云图

图7 典型拉力带平面内最大应力应变云图

图8 开圆洞钢板剪力墙塑性铰位置假设分析

假设塑性铰会出现在对角拉力带相交的位置（见图8），推测内嵌钢板的屈服应力会出现在图8（a）中灰色阴影部位，最有可能在这个区域发生破坏；假设塑性铰会出现在两条对角拉力带中心线的交点位置附近区域（图8（b）中的e、h、k、b）；或者假设应力辐射范围有一定宽度，所以塑性铰可能会出现在整个辐射范围（图8（c）中点d与f、g与i、j与l、a与c之间的区域）；也可以假设圆受到剪切变形而不是沿对角线拉伸，塑性铰出现在辐射范围某个边缘点的附近区域（图8（d）中d、i、j、c）。钢板剪力墙的剪切强度公式[8]

式 （4）中，tw为板厚；Fy为钢板屈服强度；Vsolid为非加劲钢板的剪切强度；Lcf为钢板的净宽；θ为拉力带的角度。式（5）中V为开圆洞钢板的剪力；α为退化因子；（1-α·D/Sdiag）是钢板开洞后剪切强度的折减公式，Sdiag为钢板的对角拉力带间距，D为钢板上圆孔直径，开洞率D/Sdiag在0.12到0.71时，α的值取0.7。

1.2 开圆洞钢板剪力墙的整体受力分析

开洞钢板剪力墙的整体受力性能不同于未加劲钢板剪力墙，墙板在水平荷载作用下的变形形式包括钢板和加劲肋的整体剪切变形和弯曲变形。边缘冷弯竖向加劲槽钢会对钢板的边界起到约束作用，随着层间侧移角的变大，边缘竖向加劲肋加大了对钢板的初始刚度的影响，对钢板的面外屈曲起到约束作用，确保新型开洞钢板的延性破坏。假定钢板发生塑性变形前不屈曲或者屈曲很小，不会对钢板的面内受力产生影响，借鉴文献[9]对蝴蝶形钢板墙的分析，推导开洞钢板剪力墙的初始刚度和极限承载力的理论计算公式。

1.2.1 弹性初始刚度 边缘冷弯竖向加劲槽钢与钢板完全刚接，应将钢板和槽钢作为一个整体的组合，组合截面如图9（a）所示，截面可看作为工字型截面进行类比计算。图中的组合加劲肋截面为双轴对称截面，则几何中心在y轴与z轴的交点O，中性轴为z轴。图9（b）为冷弯槽钢与钢板连接的局部图。

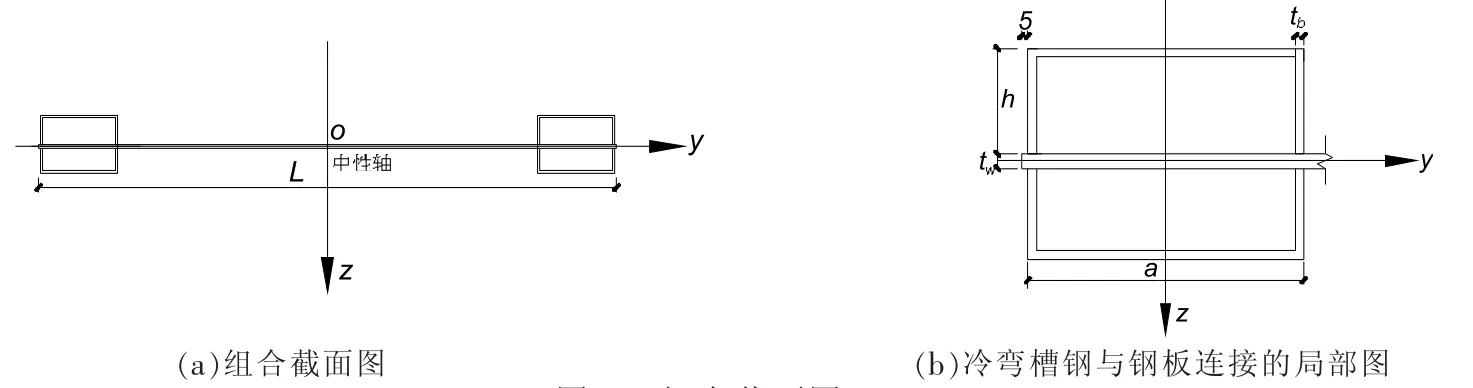
图9 组合截面图

（1）组合截面的剪切变形。假设边缘冷弯竖向加劲槽钢与钢板在荷载作用下主要发生剪切变形而不屈曲，忽略受弯变形，产生的柔度为

式（6）中，κ为组合的截面剪切形状系数，规范采用截面面积与腹板面积的比值A/Aplate来定义，κ取1.34；L为钢板剪力墙的宽度；tw为钢板剪力墙的厚度；β为钢板开圆洞面积折减系数，采用开洞后的钢板面积与钢板开圆洞前面积比值来定义；H为钢板剪力墙的高度；A0为加劲肋截面的面积；G为钢材的剪变模量。

（2）组合截面的弯曲变形。钢板两侧加劲肋与钢板一起协同工作，受力时相当于下端固定，上端滑动，端部作用有水平荷载时发生弯曲变形，按单位荷载法通过公式（7）计算得到竖向加劲钢板剪力墙的弯曲变形对钢板的总的柔度贡献为

式（7）中，H为钢板剪力墙的高度；E为钢板的弹性模量。式（8）中，IZ为组合截面绕Z轴的截面惯性矩；a为槽钢截面长。两侧冷弯槽钢加劲组合钢板剪力墙在单位荷载作用下产生的总变形是由剪切变形和弯曲变形叠加而成的，称为钢板剪力墙的柔度。则钢板剪力墙的弹性初始刚度

1.2.2 极限承载力 （1）加劲肋的极限承载力。边缘竖向冷弯加劲槽钢参与到钢板的受力，与钢板一起组成组合截面，新型开圆洞钢板剪力墙的极限承载力为加劲肋与钢板的承载力之和。

按式（10）计算组合加劲肋的截面塑性抵抗矩。

式中，ymax到z轴的最大距离，值等于L/2,则组合加劲肋的极限弯矩为

（2）总体的极限承载力。当圆孔边完全形成塑性铰时，钢板达到其极限承载力，综合考虑边缘冷弯竖向加劲槽钢的承载力可得

式（12）中，右端第一项代表组合加劲肋的抵抗贡献，它相当于只考虑一半的塑性弯矩，这由于加劲槽钢两端的边界约束复杂，加劲肋截面不可能完全进入塑性；后一项代表开圆洞钢板剪力墙的贡献，由公式（4）和公式（5）得来。

2 Base试件有限元模拟

为了进一步研究分析开圆洞钢板剪力墙的受力机理并验证上述推导的理论是否具有正确性，设计了以下试件，应用ABAQUS有限元软件对试件的刚度、承载力和耗能能力进行数值分析。

2.1 有限元试件

BASE试件采用足尺试件，高2 800 mm，宽为2 800 mm，板厚取8 mm，如图10所示。试件的高厚比λ=350（略大于300），跨高比γ=1.0。试件侧边边缘采用截面尺寸为160mm×60mm×3.5mm的冷弯槽钢加劲，正反面都设置。在钢板上沿45°对角方向交错开圆孔，圆孔直径D=200mm，对角拉力带间距Sdiag=424.26mm，开孔率D/Sdiag=0.471，圆孔间距为600 mm。冷弯加劲槽钢与内嵌钢板都选取Q235钢，Fy=235 MPa，Fu=376 MPa。材料本构关系为理想弹塑性，弹性模量E=2.06×105MPa，强化模量为0.02E，泊松比ν=0.3，图11为钢材的应力应变关系。模型为足尺钢板剪力墙，内嵌薄钢板在实际情况中施加荷载前就会因自重而产生较大的面外凹凸，在受力前就存在着微小弯曲变形（初弯曲或几何缺陷）。在钢板的几何中心施加一定大小的横向扰动荷载P来模拟其初始缺陷（主要是钢板的平面外变形）[10]。所以在模拟文中设计的试件承载力和耗能性能研究中采用该方法，对开洞钢板剪力墙施加50 kN的初始荷载以模拟其变形。

图10 开圆洞钢板剪力墙试件图

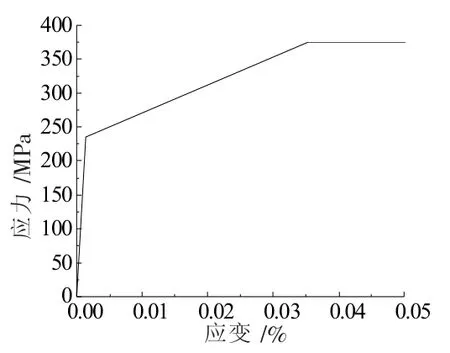
图11 钢材的应力应变关系图

2.2 试件有限元模拟分析

2.2.1 滞回曲线 采用美国ATC-24加载准则的加载方式，如表1所示。

表1 加载制度表

开圆洞钢板剪力墙有限元模拟所得滞回曲线如图12所示。由此可知，滞回曲线在加载初期具有较大的刚度，曲线呈直线，斜率大，表明钢板剪力墙处于弹性阶段。随着位移的增加，钢板发生面外屈曲变形，钢材进入弹塑性，钢板的刚度降低，表现在滞回曲线上为曲线斜率减小。由于钢板存在塑性变形，所以当荷载卸载到零时，位移并没有回到零。钢板剪力墙在零位移处表现出结构的刚度软化，滞回曲线因此出现了明显的“捏缩”现象。加载位移越大，钢板剪力墙的滞回曲线越发“饱满”。钢板剪力墙开圆洞后承载力能够在1 500 kN的大小保持稳定，并且略有提高，未出现承载力劣化的现象。

图12 开洞钢板剪力墙滞回曲线

2.2.2 骨架曲线 开圆洞钢板剪力墙的骨架曲线如图13。从图13可以看出，骨架曲线经历了弹性阶段和弹塑性阶段，钢板大约在层间位移0.125%处进入塑性耗能，直到3%层间位移时荷载都呈上升的趋势，表明钢板剪力墙在开圆洞后改善了钢板因面外变形过大而导致整体结构的承载力迅速下降，其延性性能得到改善，耗能能力也因此提高。因为钢板开圆孔后刚度虽然降低了，但圆孔分布较广，刚度削弱的范围广并且比较均匀，各应力之间的差值变小了，板中部与边缘部的变形差减小，整体的耗能性能得到增强。

图13 开圆洞钢板剪力墙骨架曲线

2.2.3 能量耗散系数 如图14所示，能量耗散系数E即每个往复加载周期内滞回环所围成的面积与卸载端至横坐标之间形成的三角形面积的比值[11]，E=SBCD+DAB/SOCF+OAE。

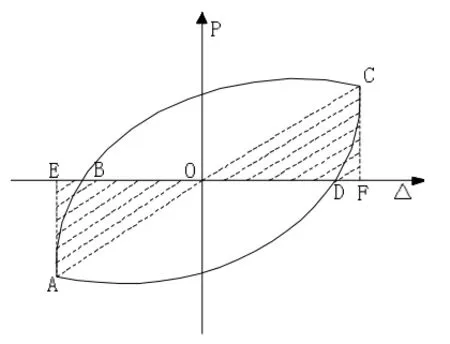
图14 能量耗散系数计算方法

开圆洞钢板剪力墙滞回环的面积随着层间位移的增加呈线性增长趋势（见图15）。开圆洞钢板剪力墙的能量耗散性能稳定，能量耗散系数呈上升趋势（见图16）。在层间位移达到2%后能量耗散系数E趋势较之前明显，表明钢板剪力墙在后期进入弹塑性耗能阶段具有更好的耗能能力。

图15 各层间位移滞回环面积

图16 各层间位移能量耗散系数

2.2.4 应力和平面外变形发展及分布 开圆洞钢板剪力墙在循环荷载作用下的各层间位移应力发展云图和平面外变形发展分布见图17和图18。圆洞打断了拉力带的传力路径，应力会集中在圆孔边缘而产生较大应力，但圆洞会使应力分布范围较广，使钢板开始屈服时应力分布均匀。钢板在各层间位移下的最大应力都出现在了在对角拉力带的圆孔边缘，并呈现出向外辐射的姿态；钢板的变形最大值也出现在了圆孔边缘，很容易在该处形成塑性铰并发生钢板的撕裂破坏。这证明了开圆洞钢板剪力墙的塑性铰位置假设理论的正确性。2.2.5 理论分析与有限元验证对比 开圆洞钢板剪力墙承载力的有限元验证值与公式（12）的计算值分别为1 570.59、1 676.44 kN，有限元值与计算值之比为0.94；初始弹性刚度的有限元验证值与公式（9）的计算值分别为310.37.59、362.32 kN·mm-1，有限元值与计算值之比为0.86。总体来看，理论值与有限元数值非常接近。对于承载力值，误差小于10%；对于初始弹性刚度，误差不超过15%。

承载力理论值偏大，理论公式是在圆孔周边形成塑性铰之前钢板不发生屈曲或者屈曲比较小的前提下成立的，它直接考虑了组合加劲肋截面1/2的塑性强度。对于第一个前提，可以通过控制圆孔的直径、圆孔的几何排列规律和钢板的宽厚比，较容易满足。而对于只考虑组合加劲肋截面1/2的塑性强度，受人为的主观臆断较严重。图17（c）和图18（c）分别给出了开圆洞钢板剪力墙在3%层间位移时的应力云图和平面外变形图，开洞钢板剪力墙中圆孔周边的应力较为集中，但冷弯侧边加劲槽钢的高应力区域主要在两端，中间部位的应力却相对小很多，这说明边缘加劲肋参与受力的程度并不清楚，造成了理论值偏小。

初始弹性刚度理论值偏大。一则文中只进行了一组开圆洞钢板剪力墙有限元模拟，模拟数据存在偶然性；二则主要借鉴文献对钢板开圆洞后刚度进行修正[9]，并不能保证其准确性；三是理论公式并没有考虑钢板剪力墙的初始面外变形。

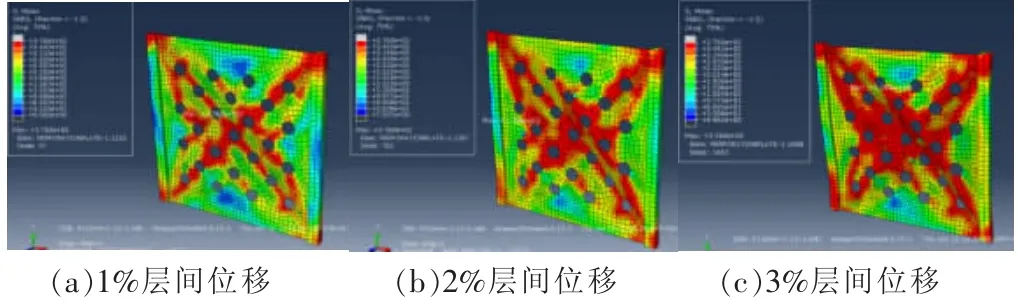
图17 开圆洞钢板剪力墙各层间位移应力发展图

图18 开圆洞钢板剪力墙各层间位移平面外变形云图

3 结论

（1）证实了开圆洞钢板剪力墙的屈服应力分布形式，其屈服分布范围广。（2）开圆洞钢板剪力墙的滞回曲线稳定饱满，在后期进入弹塑性阶段也表现出良好的耗能性能，是一种良好的耗能构件。（3）开圆洞钢板剪力墙在层间位移为0.125%时进入塑性耗能，可以先于框架梁柱发生塑性变形，作为结构的耗能构件，能够极大地减轻整体结构的破坏。（4）开圆洞钢板剪力墙的塑性铰位置假设与有限元模拟符合，证明了假设的合理性。（5）承载力和初始弹性刚度理论公式与有限元模拟比较吻合，说明理论公式具有较高的可行性。

[1]MONTGOMERY C J,MEDHEKAR M,LUBELL A S.Unstiffened steel plate shear wall performance under cyclic loading[J].Journal of Structural Engineering,2000,126（4）：453-460.

[2]Lubell A S,Prion H G L,Ventura C E.Unstiffened steel plate shear wall performance under cyclic loading[J].Journal of Structural engineering,2000,126（4）：453-460.

[3]VIAN D,BRUNEAU M.Steel plate shear walls for seismic design and retrofit of building structures[C].Multidisciplinary Center for Earthquake Engineering Research,State University of New York,Buffalo New York,2005.

[4]缪友武.两侧开缝钢板剪力墙结构性能研究[D].北京：清华大学，2004.

[5]郭彦林，缪友武，董全利.全加劲两侧开缝钢板剪力墙弹性屈曲研究[J].建筑钢结构进展，2007，38（3）：58-62.

[6]AISC341-10.Seisimic provisions for structural steel buildings[S].AISC Committee on Specifications，2010.

[7]PURBA R,BRUNEAU M.Design recommendation for perforated steel plate shearwalls[R].MCEER Report-07-0011,2007.

[8]PURBA R,BRUNEAU M.Finiteelement investigation and design recommendations for perforated steel plate shear wall[J].Journal of Structural Engineering,2009,135（11）：1367-1376.

[9]马磊，李启才.蝴蝶形钢板剪力墙的抗侧刚度和承载力研究[J].苏州科技学院学报（工程技术版），2015，28（1）：30-36.

[10]兰涛，郭彦林，郝际平，等.焊接应力对开洞钢板剪力墙极限承载力的影响[J].施工技术，2011，40（11）：62-65.

Energy dissipation capacity and bearing capacity of perforated steel plate shearwalls

LIU Jiawei,LIQicai
（School of Civil Engineering,SUST,Suzhou 215011,China）

A new perforated steel plate shear wall only connected with frame beams and stiffeners connected on two free sideswas proposed to improve the steel plate shear wall with perforation.Mechanical behavior of perforated steel plate shear walls was discussed,the plastic hinge area of the steel plate was assumed,and the initial elastic stiffness and ultimate bearing capacity theory formula of the new perforated steel plate shearwallwas proposed.To better understand themechanical properties of perforated steel plate shear wall and verify the correctness of the theoretical formula,the finite element software ABAQUSand a new method of the initial defects consideration were used.The results show that plastic hinge location assumption of perforated steel plate shear walls was verified correct;the theoretical formula greatlymatched the result from the finite element analysis;and when the steel plate got into the elastic-plastic stage,perforated steel plate shear walls showed good energy dissipation capacity.

perforated steel plate shear walls;initial elastic stiffness;ultimate bearing capacity;energy dissipation capacity

TU391

：A

：2096-3270（2017）03-0020-06

（责任编辑：秦中悦）

2016－02-17

国家自然科学基金项目（51378326）；江苏省结构工程重点实验室开放课题（ZD1204）

刘佳伟（1992-），男，江苏苏州人，硕士研究生。

李启才（1969-），男，博士，副教授，从事钢结构的新型结构体系和抗震设计研究，Email：ustsgjg@163.com。