双重介质油藏注水井试井解释模型的建立及应用*

姜 永 别旭伟 刘洪洲 王 迪 吴浩君

(中海石油(中国)有限公司天津分公司 天津 300459)

双重介质油藏注水井试井解释模型的建立及应用*

姜 永 别旭伟 刘洪洲 王 迪 吴浩君

(中海石油(中国)有限公司天津分公司 天津 300459)

姜永,别旭伟,刘洪洲，等.双重介质油藏注水井试井解释模型的建立及应用[J].中国海上油气，2017,29(4)：98-103.

JIANG Yong,BIE Xuwei,LIU Hongzhou,et al.Establishment and application of a well test interpretation model for injection wells in dual porosity reservoir [J].China Offshore Oil and Gas,2017,29(4):98-103.

针对双重介质油藏注水开发特征，基于Buckley-Leverett饱和度分布方程建立了注水井压降试井解释模型，通过Laplace变换和Stehfest数值反演对模型进行了求解，利用无因次压力降落解获得了注水井的压力降落典型图版。分析图版可知，两相区对注水井压力响应特征较大，油水黏度差异会导致双对数压力导数曲线上翘，并且两者差异越大，两相区双对数压力导数曲线上翘幅度越大，因此在试井解释时应区别储层物性变化或不渗透边界造成的压力导数曲线上翘。选取JZ油田1口注水井进行了实例应用，结果表明本文解释图版拟合结果与现场测试数据吻合较好，并且解释所得的储层参数合理。本文建立的试井解释模型可以计算注水前缘的位置，分析注水井周围地层信息及边界情况，对评价双重介质油藏注水井的动态及注水方案的设计具有重要的指导意义。

双重介质油藏；注水井；试井；解释模型；压力降落典型图版

注水井试井可以获取油相和水相渗透率、注水井周围污染情况、注水前缘距离、油藏边界等信息，为注水井措施提供依据。关于注水井试井解释方法，国内外许多学者开展了相关研究[1-4]。于九政 等[5]针对低渗透油藏注水开发特点，在考虑启动压力梯度方向性和时效性的情况下，提出了低渗储层注水井井下关井试井压力响应机理，建立了低渗储层井下关井条件下注水井的试井解释模型。刘佳洁 等[6]针对注水井试井未考虑含水率、水驱前缘等参数的问题，根据质量守恒原理，结合注水井岩心归一化相渗曲线，在油水两相区运用油水两相流渗流理论，建立了三区流体复合注水井试井模型。李乃华[7]建立了多层均质定压边界灌注试井数学模型，针对适于现场应用的折线型灌注函数，获得了层间及井底压降的实空间精确解析表达式。张艳玉 等[8]假设测试时间内地层压力均匀分布，油藏为两区复合储层模型，不考虑每个区中饱和度梯度，建立了单一介质注水井压降试井解释模型。但目前有关双重介质油藏注水井压降试井解释方法的研究较少。

为了更好地掌握双重介质地层渗流动态信息，为注水井的增注措施提供依据，本文考虑地层中饱和度梯度和注水阶段对压力降落试井的影响，建立了双重介质油藏注水井压降试井解释模型，并进行了实例应用，结果表明本文解释图版拟合结果与现场测试数据吻合较好，解释所得的储层参数合理可靠。

1 模型的建立及求解

1.1 注水阶段的物理模型

注水井物理模型见图1。

图1 注水井物理模型示意图Fig .1 Schematic of water injection well model

为研究方便，对模型作如下基本假设：

1) 地层水平等厚，油藏由裂缝系统和基质系统组成；

2) 注水井以恒定速率注水；

3) 流体和岩石微可压缩，且压缩系数为常数；

4) 流体在地层等温流动，渗流满足达西定律；

5) 忽略重力和毛细管力影响；

6) 考虑井储和表皮系数影响；

7) 水驱油为非活塞式的，裂缝系统和基质系统饱和度分布满足Buckley-Leverett方程。

1.2 注水井试井解释模型

注水阶段的物理模型假设考虑了油藏内油水饱和度的分布，为方便求解，将油水两相区剖分为N个圆环(图2)，即将连续的饱和度分布用阶梯型分布的饱和度代替，当圆环个数趋近于无限大时，阶梯型饱和度分布趋于连续的饱和度分布(图3)。

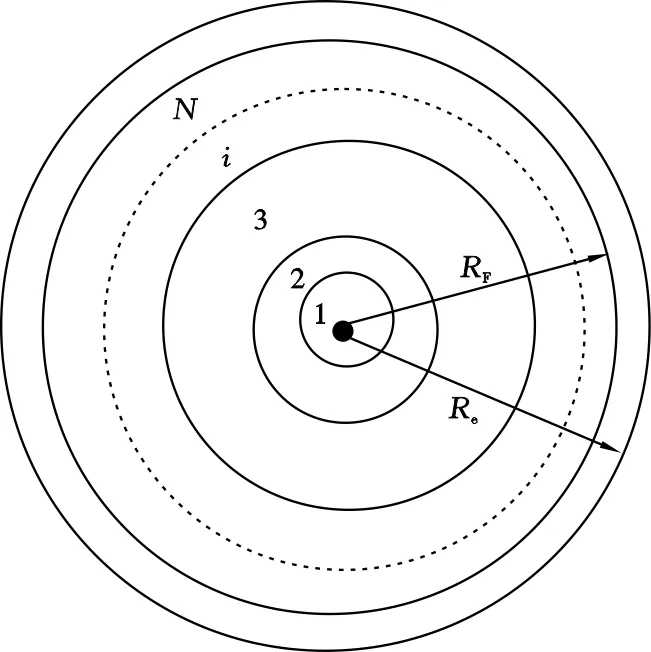
图2 油水两相区剖分为N个圆环的模型示意图Fig .2 Schematic of the post split model with Ncircular rings

图3 饱和度分布示意图Fig .3 Schematic of saturation distribution

剖分后每一圆环内的饱和度为一定值，即可认为每一圆环内的水驱油是活塞式的，其饱和度分布可由Buckley-Leverett方程确定，即

(1)

每一圆环内的饱和度为

(2)

(3)

(4)

将每个圆环内的Swi代入Buckley-Leverett方程，则可计算出每一圆环无因次半径rDi。

对于每一圆环，其扩散方程为

裂缝系统

(5)

基质系统

(6)

初始条件

(7)

内边界条件

(8)

(9)

外边界条件

1) 无限大外边界

(10)

2) 定压外边界

(11)

3) 封闭外边界

(12)

衔接条件

(13)

(14)

1.3 数学模型的求解

定义拉普拉斯变换

(15)

则数学模型可化为

裂缝系统

(16)

基质系统

(17)

整理得

(18)

内边界条件

(19)

(20)

衔接条件

(21)

(22)

外边界条件

1) 定压外边界

(23)

2) 封闭外边界

(24)

3) 无限大外边界

(25)

对于上述数学模型，其方程为一组零阶的虚宗量Bessel方程，通解为

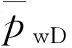
(27)

zi=(ln2/t)i

(28)

(29)

2 典型试井曲线图版分析

通过求解数学模型可以获得无因次井底压力pwD与无因次时间tD的关系。假设关井测试阶段水驱前缘不再发生变化，利用叠加原理得到关井阶段的压力降落解为

(30)

利用无因次压力降落解可获得注水井的压力降落典型图版，如图4所示，计算参数为CD=50、S=5、λ=0.000 01、ω=0.02。根据导数曲线特征可划分7个流动段,分别对应井筒储集效应阶段、表皮效应阶段、基质向裂缝窜流阶段、水区径向流阶段、油水两相区响应阶段、总系统径向流段和边界响应阶段。从图4可以看出，在窜流阶段结束后出现第1条水平直线段，表征的是井周围水区的响应；之后由于油水黏度的差异，压力导数曲线呈逐渐上翘的特征，反映的是油水两相区的响应，并且油水黏度差异越大，两相区双对数曲线上翘幅度越大(图5)。另外，水驱前缘距离越远，油水两相区时间越长，双对数曲线上到达前缘压力响应时间越晚(图6)，但不影响由于流体性质差异导致的曲线上翘幅度。因此，在试井解释时应区别储层物性变化或不渗透边界造成的压力导数曲线上翘，在到达水驱前缘后导数曲线上出现一个凸起，接着导数曲线出现第2条水平直线段，反映油区的压力响应特征。

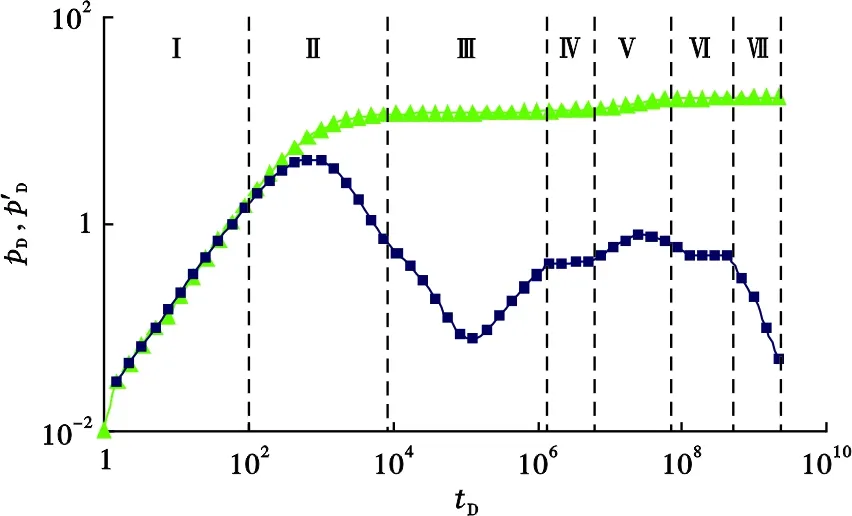
图4 双重介质油藏注水井压力降落典型曲线Fig .4 Typical pressure drop curves of an injection well in fractured reservoir

图5 油水黏度差异对双重介质油藏注水井压力降落 典型曲线的影响Fig .5 Effect of oil viscosity difference on typical pressure drop curves of an injection well in fractured reservoir

图6 水驱前缘对双重介质油藏注水井压力降落 典型曲线的影响Fig .6 Effect of water flooding front on typical pressure drop curves of an injection well in fractured reservoir

3 实例应用

JZ油田一口注水井X井，在进行压力降落测试前平均日注水256 m3，注水2个月累注水1.54×104m3。该注水井及油藏基本参数见表1，地层流体的相对渗透率曲线及地层分流率曲线见图7。

该注水井实测压力数据与本文典型图版拟合情况见图8，可以看出，两者吻合较好。根据压力拟合可计算出残余油饱和度下的水相渗透率，根据时间拟合可计算出前缘的位置[8]。该注水井最终解释参数值见表2，可以看出，储层物性较好，注水井存在一定程度污染，水驱波及距离达到183 m。

表1 注水井X井及油藏基本参数Table 1 Basic parameters of the injection Well X and the reservoir

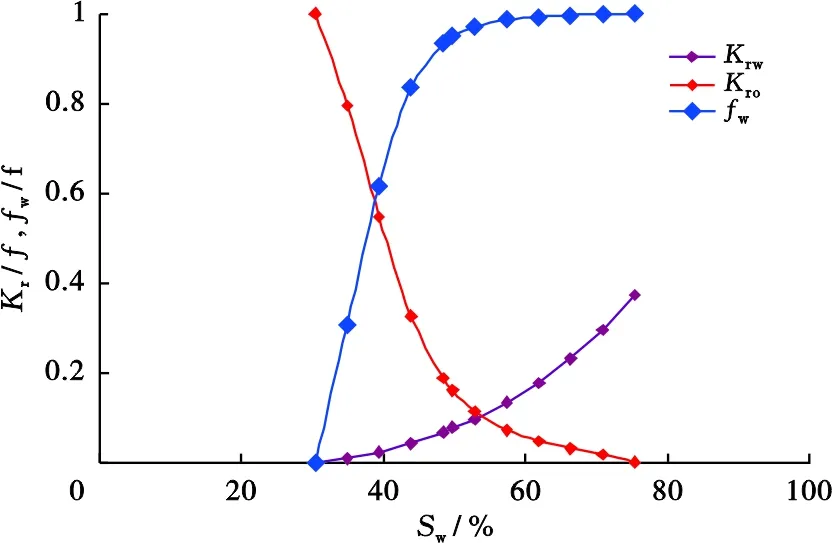
图7 注水井X井相对渗透率曲线和地层分流率曲线Fig .7 Relative permeability curve and water diversion rate curve of the injection Well X

图8 注水井X井压降曲线与典型图版拟合图Fig .8 Fitting chart of pressure drop curves of the injection Well X with typical curves表2 注水井X井试井解释结果Table 2 Well test interpretation results of the injection Well X

参数数值参数数值地层渗透率/mD382井储系数/(m3·MPa-1)0.15油相渗透率/mD163窜流系数0.0003水相渗透率/mD206弹性储能比0.16前缘距离/m183地层压力/MPa15.0表皮系数6.3

4 结论

1) 基于Buckley-Leverett饱和度分布方程建立了双重介质油藏注水井压降试井解释模型，通过Laplace变换和Stehfest数值反演对模型进行了求解，得到了注水井的压力降落典型图版。分析图版可知，两相区对注水井压力响应特征较大，油水黏度差异会导致双对数曲线上翘，并且油水黏度差异越大，两相区双对数曲线上翘幅度越大，因此在试井解释时应区别储层物性变化或不渗透边界造成的压力导数曲线上翘。

2) 利用本文建立的试井解释模型可以计算注水前缘的位置，分析注水井周围地层信息及边界情况。实例应用表明，本文解释图版拟合结果与现场测试数据吻合较好，解释所得的储层参数合理可靠。

符号注释

Sw—含水饱和度，%；

rD(Sw)—Sw所对应的无因次距离；

q—注水量，m3/d；

tp—注水时间，h；

h—油藏厚度，m；

rw—井半径，m；

Sor—残余油饱和度，%；

SwF—水驱油前缘饱和度，%；

Kf—裂缝渗透率，D；

K—地层平均渗透率，D；

λ—窜流系数；

φf—裂缝孔隙度,%；

φ—地层孔隙度,%；

Ctf—裂缝系统压缩系数,1/MPa；

Ct—地层综合压缩系数,1/MPa；

μ—流体黏度,mPa·s；

re—油藏半径，m；

B—体积系数,m3/m3；

t—时间，h；

S—表皮系数,无因次；

CD—无因次井筒储存系数；

pi—原始地层压力,MPa；

z—拉普拉斯变量；

I0、K0—第1类、第2类零阶修正贝塞尔函数；

Ai、Bi—待定常数；

rDf—水驱油前缘无因次距离。

[1] 尹洪军,付春权,万贵春，等.多重复合低渗透油藏注水井压力动态分析[J].石油学报,2002,23(4):70-74.YINHongjun,FUChunquan,WANGuichun,etal.Pressuretransientanalysisofwaterinjectionwellinmultiplecompositelowpermeabilityreservoir[J].ActaPetroleiSinica,2002,23(4):70-74.

[2] 巨亚锋，于九政，郭方元，等.低渗两区复合油藏注水井试井解释模型[J].石油天然气学报(江汉石油学院学报),2012,34(7):109-113.JU Yafeng，YU Jiuzheng，GUO Fangyuan，et al.Well-test interpretation model for water injection wells in two-regional low permeability composite reservoirs [J].Journal of Oil and Gas Technology(J.JPI),2012,34(7):109-113.

[3] 尹洪军，曾昭英，刘义坤，等.合理利用典型曲线分析注水井试井资料的方法[J].大庆石油学院学报,1993,17(2):112-114.YIN Hongjun,ZENG Zhaoying，LIU Yikun，et al.A method for analyzing well test data of water injection wells by using type curves reasonably [J].Journal of Daqing Petroleum Institute,1993,17(2):112-114.

[4] 刘佳洁,孟英峰,李皋，等.基于油水两相渗流的地层流体复合注水井试井模型[J].石油天然气学报(江汉石油学院学报),2014,36(2):128-132.LIU Jiajie,MENG Yingfeng，LI Gao，et al.Composite well test model based on oil-water two-phase flow for injection wells[J].Journal of Oil and Gas Technology(J.JPI),2014,36(2):128-132.

[5] 于九政，晏耿成，巨亚锋，等.低渗油藏注水井试井压力响应机理及解释模型[J].断块油气田,2013,20(1):92-95.YU Jiuzheng，YAN Gengcheng，JU Yafeng，et al.Response mechanism and interpretation model of water injection well testing pressure in low permeability reservoir [J].Fault-Block Oil and Gas Field,2013,20(1):92-95.

[6] 刘佳洁,孟英峰,李皋，等.三区流体复合注水井试井模型研究[J].石油天然气学报(江汉石油学院学报),2013,35(2):120-125.LIU Jiajie,MENG Yingfeng,LI Gao，et al.Three-zone fluid composite well test model of injection wells[J].Journal of Oil and Gas Technology(J.JPI),2013,35(2):120-125.

[7] 李乃华.多层定压边界灌注井数学模型[J].河北工业大学学报,2006,35(5):32-35.LI Naihua.Mathematical model of the injection well testing for layers with constant pressure[J].Journal of Hebei University of Technology,2006,35(5):32-35.

[8] 张艳玉,姚军.现代试井解释原理与方法[M].北京:中国石油大学出版社,2006.

[9] 贾永禄,聂仁仕,王永恒，等.二次梯度非线性渗流问题求解[J].石油天然气学报(江汉石油学院学报),2008,30(4):119-123.JIA Yonglu,NIE Renshi,WANG Yongheng,et al.Solution for the problem of quadratic gradient nonlinear percolation[J].Journal of Oil and Gas Technology(J.JPI),2008,30(4):119-123.

[10] 刘永良,刘彬，刘大伟，等.三重介质气藏单井生产动态分析模型研究[J].石油天然气学报(江汉石油学院学报)，2011,33(2):123-127.LIU Yongliang,LIU Bin，LIU Dawei，et al.Analytic model of single well production performance in triple porosity medium reservoirs [J].Journal of Oil and Gas Technology(J.JPI),2011,33(2):123-127.

[11] 胡建国.圆形定压边界油藏试井分析方法[J].中国海上油气(地质),1997,11(5):355-363.HU Jianguo.A method of well-test analysis for a circular reservoir with a constant pressure outer boundary [J].China Offshore Oil and Oas(Geology),1997,11(5):355-363.

[12] 廖新维,陈钦雷.均质油藏斜井试井模型研究[J].中国海上油气(地质),1998,12(5):332-338.LIAO Xinwei,CHEN Qinlei.Discussion on well test model of homogeneous reservoir in slanted well[J].China Offshore Oil and Gas(Geology),1998,12(5):332-338.

[13] 贾永禄,赵必荣.拉普拉斯变换及数值反演在试井分析中的应用[J].天然气工业,1992,12(1):60-64.JIA Yonglu,ZHAO Birong.Application of Laplace transform and numerical inversion to well test analysis [J].Natural Gas Industry,1992,12(1):60-64.

(编辑：杨 滨)

Establishment and application of a well test interpretation model for injection wells in dual porosity reservoir

JIANG Yong BIE Xuwei LIU Hongzhou WANG Di WU Haojun

(TianjinBranchofCNOOCLtd.,Tianjin300459,China)

Based on water flooding characteristics of dual porosity reservoir and Buckley-Leverett equation, the injection pressure drop testing interpretation model is established.Laplace transform and Stehfest numerical inversion are used to solve the model and a pressure drop typical plate of injection well is obtained with dimensionless pressure drop solution.Results show that oil-water two-phase region has large pressure response characteristics, oil-water viscosity difference causes double logarithmic curve upward.The larger the difference of oil-water viscosity, the more two-phase double logarithmic curve upturns.So the upward curve caused by reservoir change or impermeability boundary should be distinguished.The application in an injection well of JZ oilfield shows that the interpretation results agree with field test data.The proposed model can be used to calculate the position of water flood front, and to analyze the formation around the injection well and boundary condition, thus guiding water injection well evaluation and the design of injection scheme.

dual porosity reservoir; water injection well; well test; interpretation model; typical chart of pressure drop

*国家自然科学基金重点项目“储层裂缝形成机理(编号：40772089)”部分研究成果。

姜永，男，工程师，硕士，主要从事试井、油藏工程方面的研究工作。地址：天津市滨海新区海川路2121号渤海石油管理局B座(邮编：300459)。E-mail：jiangyong198786858@163.com。

1673-1506(2017)04-0098-06

10.11935/j.issn.1673-1506.2017.04.012

TE344

A

2017-01-12 改回日期：2017-03-31