螺旋射孔多孔眼起裂裂缝形态有限元模拟*

单清林 金 衍 王亚军 张 翔 张儒鑫 吴 越 娄尔标 周华波

(1.中国石油大学(北京)油气资源与工程国家重点实验室 北京 102249； 2.中国石油长庆油田分公司 陕西西安 710016；3.中国石油塔里木油田分公司 新疆库尔勒 841000； 4.中国石油集团渤海钻探工程有限公司 天津 300457)

螺旋射孔多孔眼起裂裂缝形态有限元模拟*

单清林1金 衍1王亚军2张 翔2张儒鑫1吴 越1娄尔标3周华波4

(1.中国石油大学(北京)油气资源与工程国家重点实验室 北京 102249； 2.中国石油长庆油田分公司 陕西西安 710016；3.中国石油塔里木油田分公司 新疆库尔勒 841000； 4.中国石油集团渤海钻探工程有限公司 天津 300457)

单清林,金衍,王亚军，等.螺旋射孔多孔眼起裂裂缝形态有限元模拟[J].中国海上油气，2017,29(4)：123-130.

SHAN Qinglin,JIN Yan,WANG Yajun,et al.Finite element simulation of fracture initiation from multiple perforation channels of spiral pattern[J].China Offshore Oil and Gas,2017,29(4):123-130.

采用螺旋射孔完井时，准确模拟不同孔眼周围裂缝的起裂形态能够有效指导射孔参数的优化。基于渗流-应力耦合方法建立螺旋射孔井有限元数值模型，引入损伤变量描述岩体破坏后的弹性参数、强度和渗透率随损伤的变化规律，进一步追踪模拟岩体损伤裂隙的演变过程，借此预测近井筒周围的水力裂缝起裂和扩展形态。模拟结果表明：采用耦合损伤变量的有限元模型能够模拟出沿井筒面和射孔方向扩展的两种水力裂缝的起裂及其随液压加载的扩展趋势；针对不同井筒方向条件可模拟出不同孔眼处水力裂缝的起裂差异，以此评估孔眼间水力连接性，并预测近井筒裂缝形态。室内物理模拟实验与数值模拟结果一致，表明建立的有限元数值模型可用于分析近井筒裂缝起裂的复杂性问题，对现场射孔压裂优化设计具有指导意义。

螺旋射孔完井；有限元模型；损伤变量；近井筒水力裂缝；物理模拟实验

水力压裂技术是开发非常规油气藏的常用技术，压裂之前通常采用固井加射孔的技术以保持井壁稳定，并实现井筒与地层的水力沟通。由于存在对储层地应力特征把握不准的可能性，现场多采用螺旋射孔技术增加孔眼方向与最优射孔方向吻合的概率。对于射孔井水力压裂，除起裂压力为压裂设计的重要参数之外，井眼周围的裂缝复杂程度也是影响压裂效果的重要因素。因此，建立数值模型实现对近井水力裂缝起裂和扩展的模拟，对于射孔井压裂的优化设计，减少近井筒裂缝复杂形态具有重要意义。前人对水力裂缝起裂和裂缝形态也进行了理论分析、物理模拟实验和数值模拟方法等多方面的研究。大多数理论分析是将井筒与射孔简化为2个正交的圆柱，采用平面应变假设计算井筒周围应力分布，在此基础上对射孔周围应力分布进行计算，其中Hossain[1]采用该方法建立了射孔斜井破裂压力的预测模型，实现了对斜井不同井斜、走向和射孔方位条件下破裂压力的预测，但由于射孔与井筒相交的部位并不满足平面应变假设，该方法对应力分布的计算并不准确；Fallahzadeh等[2]采用同样的方法，进一步考虑了套管和水泥环对裂缝起裂的影响。物理模拟实验方法可以在实验室尺度条件下直观地对裂缝的形态进行模拟，如Behrmann等[3]采用室内实验模拟了现场钻井、固井和压裂的施工流程，并对不同地应力条件和射孔方位条件下的裂缝形态进行了分析。数值模拟方法多集中于有限元方法和边界元方法的应用，该方法可以避免理论分析方法中由于假设所带来的计算误差，其中Papanastasiou等[4]采用三维边界元方法计算了射孔井孔眼周围的应力分布，对井眼破裂压力和出砂的可能性进行了预测；Quattlebaum等[5]采用三维有限元方法计算了射孔孔眼孔径不同对水平井起裂压力分布的影响，并针对近井筒裂缝复杂性问题提供了工程优化建议。近年来，Aidagulov等[6]对传统最大拉应力准则在预测复杂井筒模型起裂压力的准确性时提出了疑问，采用平均应力方法(SAMTS)取得了较好的预测效果。相比理论分析和物理模拟实验，数值模拟方法不受几何形状和尺寸因素的限制，有很大灵活性。但传统基于最大拉应力准则的有限元方法模拟射孔压裂时，仅对射孔与井筒壁面的应力分布进行计算，无法实现对近井筒裂缝形态的准确预测，其结果具有局限性。笔者在前人研究基础上，引入损伤变量建立了耦合损伤变量的有限元模型来模拟岩石力学与渗流性质随岩体损伤变化的规律，以此追踪岩体在水力致裂后的损伤演变过程，考察近井筒水力裂缝的起裂和扩展规律，并采用物理模拟实验对模型的有效性进行验证，以期为现场压裂设计提供借鉴。

1 耦合损伤变量的有限元模型建立

模型中岩石材料假设为均质硬脆性孔弹性介质，考虑流固耦合作用对模型应力场的影响以提高结果的准确性，有限元计算中控制方程与连续性方程如式(1)所示[7]。

(1)

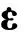
为预测裂缝起裂后的扩展形态，对模型引入损伤变量。Okubo等[8]进行的岩石单轴拉伸实验表明，岩石破坏后依然保留一定的残余强度，并且岩石的单轴拉伸曲线形态与单轴压缩曲线形态相似。参照前人的实验结果，为预测岩石的拉伸或剪切破坏，采用Drucker-Prager强度准则(D-P准则)，屈服方程如式(2)所示[9]。

(2)

式(2)中：q为偏应力；K为材料参数，表示材料三轴拉伸与三轴压缩的强度之比；r为第三应力不变量；σm为平均应力；φ和d分别为摩擦角和黏聚力。

采用强度和刚度衰减方法模拟岩石达到强度极限后软化过程，如式(3)所示[10-11]。

(3)

式(3)中：D为损伤变量；E和E0分别为岩石损伤后的弹性模量和初始弹性模量；f和f0分别为岩石损伤后的强度和初始强度。

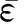
(4)

同时，由于损伤，岩石的渗透性也会发生变化，按照渗流的立方体定律[13]，损伤后岩石的渗透系数为

(5)

2 数值模拟分析

2.1 模型参数设置

基于ABAQUS软件平台建立有限元模型，模型以正断层地应力条件下深度4 000 m假想致密砂岩储层为研究对象。模型计算过程中，井筒附近应力模拟的准确性可影响到每个射孔部位的应力计算，而井筒周围应力计算结果受模型尺寸影响，因此取半径为3 m、厚度为2 m的圆盘状块体建模(模型半径超过井筒半径20倍，经试算该模型尺寸足以消除边界对井筒周围应力及渗流范围等计算结果的影响)。为简化计算，仅设置6个射孔位于模型中央(图1)，取常用的60°相位，并保证其中2个孔眼位于过井筒轴线的竖直平面内，以消除射孔方向对模型结果的影响。套管、井筒和射孔尺寸参数均参考现场实际情况(表1)，模型中材料参数如表2所示，表征岩石损伤的参数参考前人实验及数值模拟参数进行设定[8,11](表3)。假定水平井方位与最小水平主地应力方向一致(图1)，三向地应力分别为σv=100 MPa、σH=75 MPa、σh=65 MPa。孔隙压力为pp=50 MPa。采用有限元方法建模，并进行二次开发将损伤变量及其对材料力学和渗流性质的影响引入模型中。

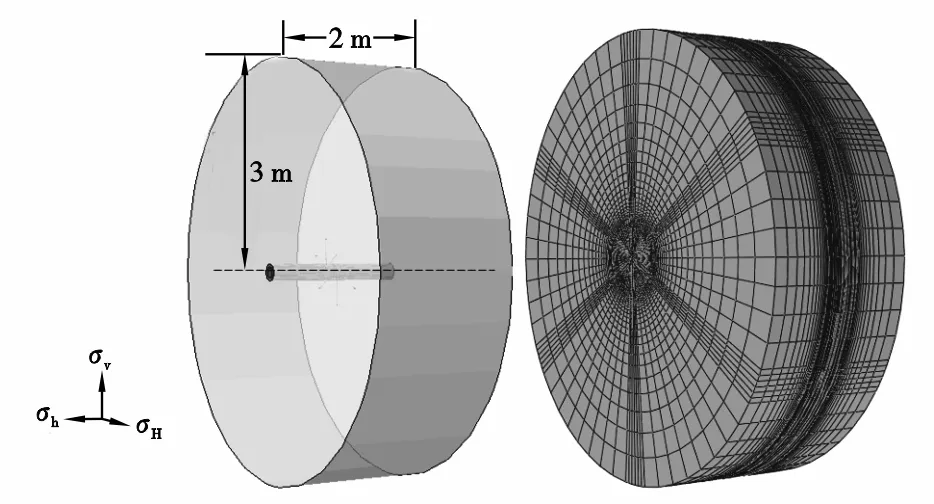
图1 有限元几何模型与网格划分Fig .1 Finite element mesh configuration表1 模型主要几何参数Table 1 Model geometric parameters

参数数值井眼直径/mm215套管外径/mm139.7射孔密度/(孔·m-1)16射孔相位/(°)60射孔长度/mm350射孔孔径/mm14

表2 模型材料参数Table 2 Model material parameters

表3 岩石材料的损伤表征参数Table 3 Rock damage relative parameters

2.2 结果分析

图2为随井底流压增加，井筒周围岩体损伤发生和演变过程，可以看出：井底压力增至70 MPa时，与水平面呈30°夹角的射孔孔眼根部优先起裂(图2a)；之后所有射孔孔眼的根部均起裂，但裂缝并没有沿射孔方向扩展，而是沿井筒壁面发展(图2b)；井底压力增至91 MPa时，井筒顶部与底部的孔眼优先发展出由射孔根部起裂，并沿射孔方向发展的水力裂缝(图2c)；井底压力为92 MPa时，井筒侧面的孔眼也起裂出沿射孔方向发展的水力裂缝(图2d)；井底压力为96 MPa时，由于模型中出现大变形，无法收敛而停止计算，从而得到最终的近井筒初始水力裂缝形态(图2e)。

从图2结果分析可以得出，裂缝扩展模式有2种，一种是沿井筒壁面发展的裂缝，另一种是后出现的沿射孔方向扩展的裂缝。第一种裂缝形态可为微环隙的产生提供解释，如Behrmann和Warpinski的实验观测结果[3,14]；第二种裂缝相比于第一种更有机会扩展生成主水力裂缝面，即压裂过程中首先产生的裂缝不一定为能够突破近井筒应力集中区域的水力裂缝，可能仅为沿井筒壁面发展的微环隙裂缝。图2中，井底压力为70～91 MPa时裂缝形态为沿井筒壁面发展的水力裂缝产生和扩展阶段，真正产生沿射孔方向扩展并能突破近井筒应力集中区域的主水力裂缝起始于井底压力升至91 MPa时，因此真实起裂压力应为91～96 MPa。可见，本文方法较传统有限元方法可实现对螺旋射孔井起裂压力的合理预测。

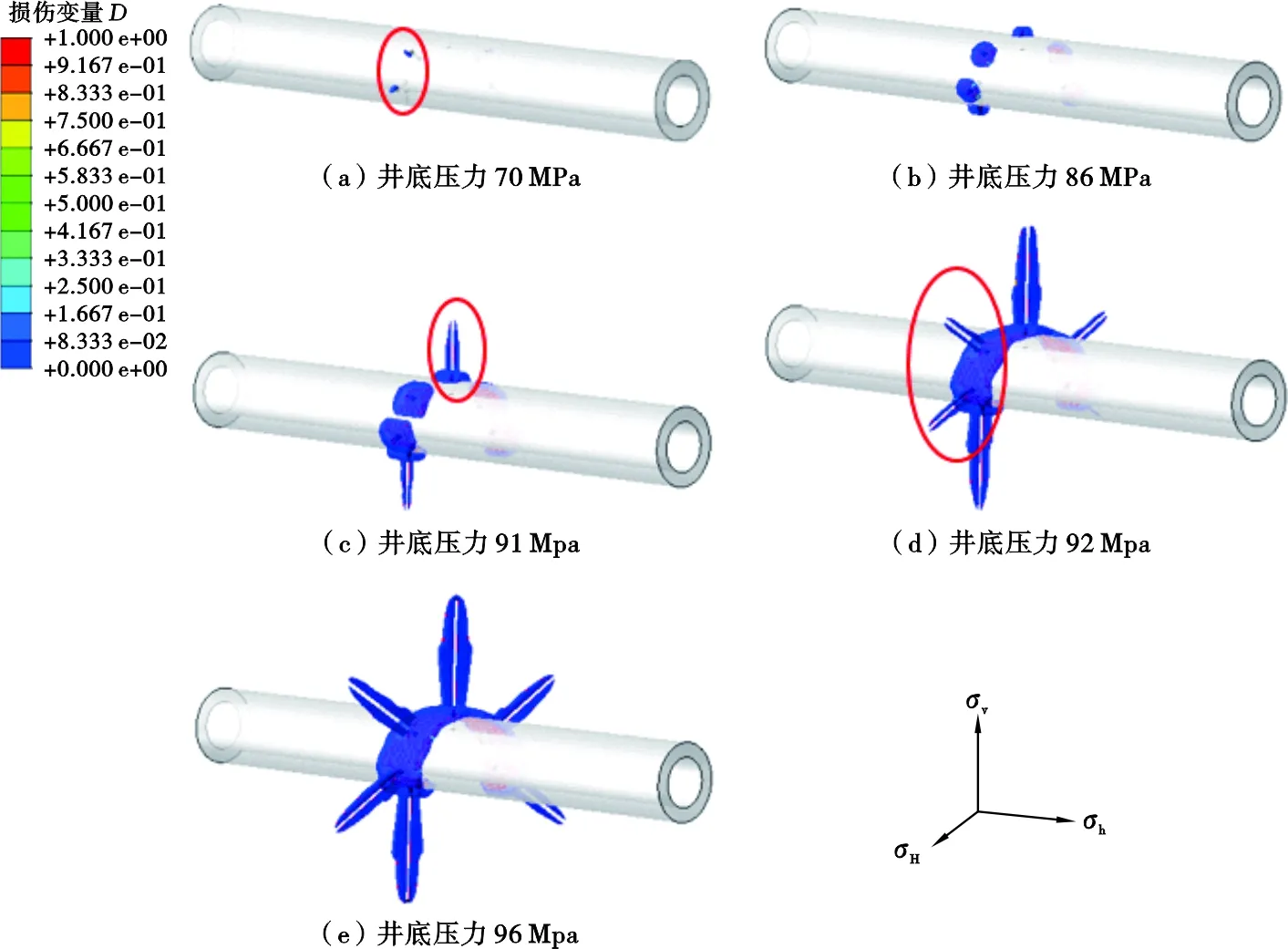
图2 井底压力不断增加条件下井筒周围岩体损伤发生与发展过程Fig .2 Evolution of damage around the wellbore and perforations with increasment of BHP

图2中每个射孔的初始裂缝面相互平行，裂缝尺寸相近，裂缝面法向均与最小水平地应力方向一致。因此，当射孔密度比较低时，射孔间的相互作用弱，水力裂缝从射孔起裂后会倾向独立扩展，或者在优先起裂的裂缝对其他裂缝抑制作用下形成单一裂缝面，或者形成分层的裂缝面；如果射孔密度足够高，相邻射孔孔眼起裂的水力裂缝面会相互融合并形成螺旋式的裂缝面。

图3为不同井眼走向和倾角条件下近井筒初始水力裂缝形态的有限元模拟结果，可以看出：当保持井眼水平，增大井眼方向与最小水平地应力的夹角时，井筒两侧的射孔孔眼倾向于不发生起裂，当井筒与最小水平地应力夹角为60°时，只有井筒顶部和底部的射孔发生起裂，裂缝面法向相对井筒方向发生偏转并保持与最小水平地应力方向一致(图3a—c)。保持井眼沿最小水平地应力方位不变，改变井筒与水平面的夹角时，井筒顶部与底部的射孔倾向于不起裂，井筒侧面射孔起裂的裂缝面法向相对井筒方向发生偏转，且裂缝面保持竖直(图3d—f)。

根据图3所示的2种变化条件下的裂缝形态，可推测极限情况下(α=90°且β=0°，α=0°且β=90°)，两者均将产生沿井筒轴线方向扩展的裂缝面。其中，起裂孔眼射孔方向与垂直井筒两主地应力的较大者一致或呈较小夹角，即α=90°且β=0°条件下原井筒顶部和底部的孔眼起裂；α=0°且β=90°条件下原井筒侧向的孔眼起裂，这与前人有关最优射孔方位及裂缝形态预测的分析结果一致[3,15]，说明有限元方法的结果是合理的。

在非极限情况条件下(0°<α<90°或 0°<β<90°)，由于存在起裂不完全或不起裂的孔眼，会影响邻近孔眼水力裂缝之间的相互沟通。如在图3a—c情况中，井筒顶部与底部的射孔起裂，而侧向的射孔倾向不起裂，则可预测顶部与底部射孔处裂缝起裂后，两者之间由于缺少侧向孔眼裂缝的过渡连接作用，不容易产生如图3a所预测的螺旋裂缝面，2条裂缝倾向于独立扩展而在近井筒产生分层的裂缝面，如图4a所示。而在图3d—f情况中，裂缝倾向于从侧面的射孔孔眼起裂，在近井筒产生裂缝重叠区域，若两孔眼相邻，则两裂缝最终会发生融合，如图4b所示。

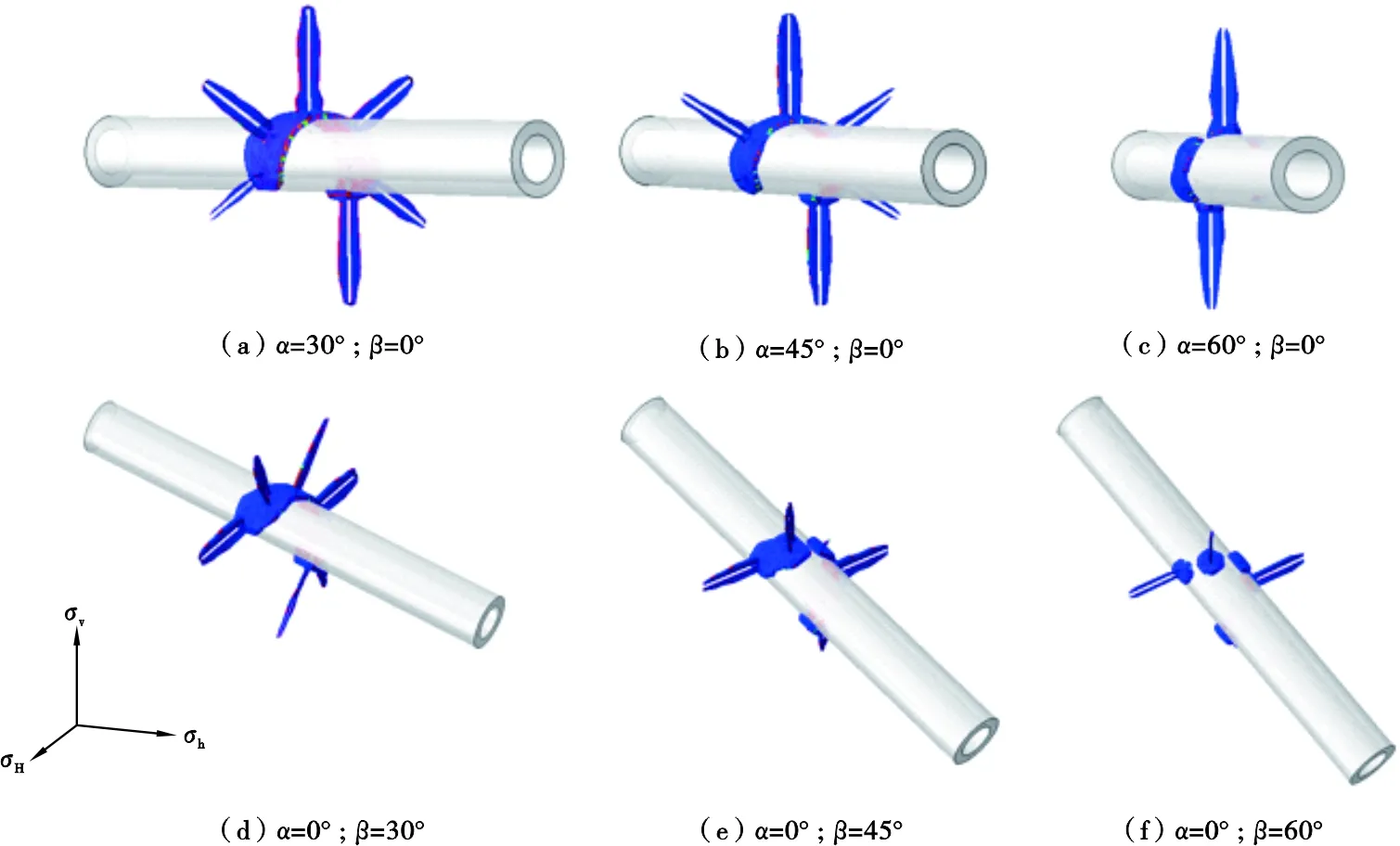
图3 不同井眼倾向与走向条件下近井筒初始裂缝形态(α表示井眼轴线在水平面上的投影与最小水平地应力 方向的夹角，β表示井筒与水平方向夹角)Fig .3 Initial fracture geometry around wellbores with different wellbore directions(α indicates the angle between the projection of wellbore and the minimum horizontal stress onto a horizontal plane,β indicates the angle between the wellbore and the horizontal stress)

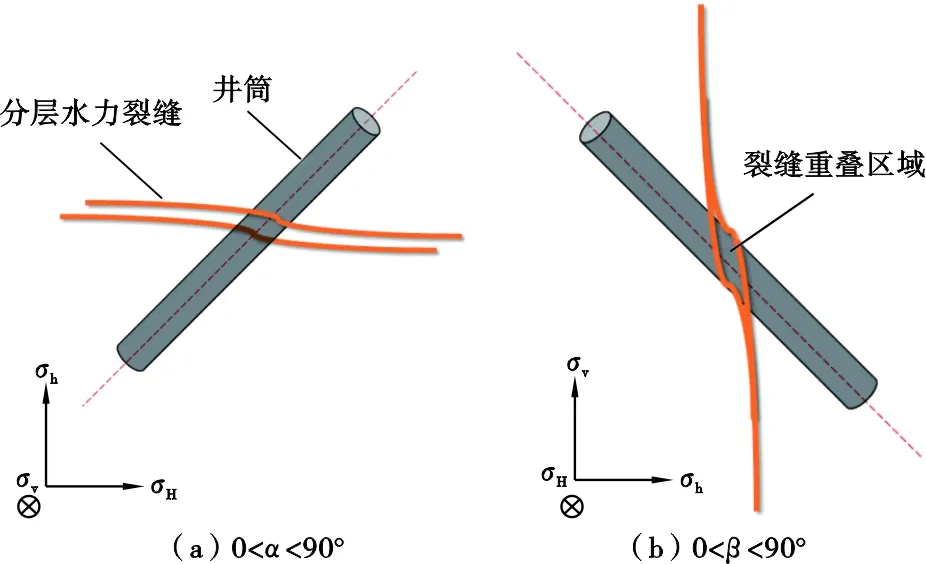
图4 基于数值模拟结果预测不同井眼方向条件下的 近井筒裂缝形态Fig .4 Initial fracture geometry around the wellbores with different orientations speculated by numerical model

3 物理模拟实验验证

为进一步验证有限元方法的有效性，进行了4组物理模拟实验。实验采用大尺寸真三轴模拟试验系统，该系统由大尺寸真三轴试验架、MTS伺服增压泵、稳压源、油水隔离器及其他辅助装置组成[16]。由于有限元模型针对现场尺度建模，需依据相似准则将地应力及液压加载速率等参数转换至实验室尺度，以便于实验后将物理模拟结果与数值模拟结果进行对比。

3.1 实验参数设置

采用外径14 mm、内径10 mm的钢管模拟井筒，在井筒上钻孔并塞入纸轴以模拟射孔，如图5所示。表4为实验方案，实验参数基于数值模型数据，采用相似理论转化至实验室尺度[17]。实验所用的混凝土试件尺寸为300 mm×300 mm×300 mm，采用325号水泥与石英砂按质量比1∶1浇筑凝固而成，试件基本参数如表5所示。

3.2 实验结果分析

实验结果见表6，实验裂缝形态如图6所示。实验1与实验2井眼均沿着最小水平地应力方向，射孔密度不同造成裂缝面形状的差异(图6a、b)。实验1中射孔密度低(模拟现场螺旋射孔密度为10孔/m的情况)，射孔间初始水力裂缝无法有效沟通，水力裂缝从其中一个孔眼起裂后迅速扩展至试件边界，形成平整的裂缝面；实验2的射孔密度是实验1的1.6倍(模拟现场螺旋射孔密度为16孔/m的情况)，射孔密度的增加促进了射孔间初始水力裂缝的相互连接，从而形成围绕井筒的螺旋式射孔面。这说明，当井眼方位与最小水平地应力方向一致时，各射孔孔眼起裂几率相当，裂缝面形状与射孔密度相关，适当增加射孔密度会增加裂缝融合的几率，这一结果与有限元方法分析结果一致。此外，根据Veeken等[18-22]的观点，为减小近井筒裂缝复杂性，应尽量使主水力裂缝沟通尽量多的射孔孔眼，并尽量减少裂缝重叠现象。因此，根据实验1与实验2的结论，现场压裂施工采用60°相位螺旋射孔方式时，射孔密度不宜过低，至少不应低于10孔/m。

图5 井筒及模具组合(左为直井筒，右为斜井筒)Fig .5 Assembly of wellbore and cast model(the left one with a straight wellbore,and the right one with the deviated wellbore)表4 螺旋射孔水力压裂实验参数Table 4 Experiment parameters of spiral perforating hydraulic fracturing experiments

实验编号地应力/MPa射孔参数σvσHσh孔长/cm孔径/mm孔密/(孔·cm-1)井眼方位(α;β)/(°)压裂液黏度/(mPa·s)排量/(mL·s-1)11 0;02282219321.6 0;01200.3331.645;041.6 0;45

表5 螺旋射孔水力压裂实验试件基本参数Table 5 Basic parameters of spiral perforating hydraulic fracturing experiments samples

表6 螺旋射孔水力压裂实验结果Table 6 Experiment results of spiral perforating hydraulic fracturing experiments

实验3和实验4所得裂缝形态(图6c、d)与Van Ketterij等[19]进行的射孔对裂缝形态影响的部分实验结果类似，即若起裂孔眼间存在空间距离，由于裂缝间水力连通性降低，易导致裂缝重叠现象。实验3中，由于射孔孔眼起裂不均匀，造成了多层裂缝的近井筒复杂裂缝形态。实验4中，水力裂缝从井筒侧向的两孔眼分别起裂后，2条裂缝合并形成主裂缝面并与井筒顶部的一个孔眼相交，在近井筒形成了局部裂缝重叠区域。实验3和实验4结果与有限元分析结果大体一致，进一步验证了耦合损伤变量的有限元模型对近井筒初始裂缝形态预测结果的有效性。由于有限元模型不受几何模型复杂程度的限制，本文模拟方法可以推广至其他井眼轨迹及射孔方式下初始水力裂缝形态的模拟，从而为射孔方式的优选优化，避免近井筒复杂裂缝形态提供参考。

图6 螺旋射孔水力压裂实验中井筒周围裂缝形态Fig .6 Fracture patterns around the wellbores of spiral perforating hyclraulic fracturing experiments

4 结论

1) 在有限元方法基础上，引入损伤变量对岩石破坏后的强度、弹性参数和渗透率特征进行描述，可实现对射孔井近井筒岩体损伤演化过程进行追踪。与传统有限元方法相比，采用耦合损伤变量的有限元模型能够模拟出近井筒岩体损伤的动态扩展过程，可方便地辨别出不同类型裂缝的起裂规律。

2) 针对相位角为60°的螺旋射孔方式，采用耦合损伤变量的有限元模型模拟了不同井筒方向的近井筒初始水力裂缝，并根据不同孔眼位置裂缝的起裂次序和裂缝形态，对近井筒裂缝复杂性进行分析预测，而且物理模拟实验结果验证了该数值模拟方法的有效性。

3) 由于有限元方法几何建模方面的灵活性，本文模拟方法可推广至不同井型和射孔方式条件下初始裂缝的模拟，可针对特定储层、地应力和井眼轨迹条件，对不同射孔方式所产生的近井筒水力裂缝形态进行预测，优选优化射孔参数，为避免近井筒复杂裂缝形态提供参考。

[1] HOSSAIN M M,RAHMAN M K,RAHMAN S S.Hydraulic fracture initiation and propagation:roles of wellbore trajectory,perforation and stress regimes[J].Journal of Petroleum Science and Engineering,2000,27(3):129-149.

[2] FALLAHZADEH S A H,SHADIZADEH R S,POURAFSHARY P,et al.Dealing with the challenges of hydraulic fracture initiation in deviated-cased perforated boreholes[R].SPE 132797,2010.

[3] BEHRMANN L A,ELBEL J L.Effect of perforations on fracture initiation[J].Journal of Petroleum Technology,1991,43(5):608-615.

[4] PAPANASTASIOU P,ZERVOS A,OTHERS.Three-dimensional stress analysis of a wellbore with perforations and a fracture[R].SPE 47378,1998.

[5] QUATTLEBAUM C,BORGEN K L,XUE Z,et al.Optimizing perforating charge design for stimulation[R].SPE 159085,2012.

[6] AIDAGULOV G,ALEKSEENKO O,CHANG F F,et al.Model of hydraulic fracture initiation from the notched open hole[R].SPE 178027,2015.

[7] XU B,WONG R C K.A 3D finite element model for history matching hydraulic fracturing in unconsolidated sands formation[J].Journal of Canadian Petroleum Technology,2010,49(4):58-66.

[8] OKUBO S,FUKUI K.Complete stress-strain curves for various rock types in uniaxial tension[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1996,33(6):549-556.

[9] HIBBITT D,KARLSSON B,SORENSEN P.Abaqus/CAE user’s guide,ABAQUS 6.11[M].Dassault Systèmes Simulia Corp.:Providence,RI,USA,2013.

[10] ZHU W C,TANG C A.Numerical simulation of Brazilian disk rock failure under static and dynamic loading[J].International Journal of Rock Mechanics and Mining Sciences,2006,43(2):236-252.

[11] TANG C A,THAM L G,LEE P,et al.Coupled analysis of flow,stress and damage (FSD) in rock failure[J].International Journal of Rock Mechanics and Mining Sciences,2002,39(4):477-489.

[12] LUBLINER J,OLIVER J,OLLER S,et al.A plastic-damage model for concrete[J].International Journal of Solids and Structures,1989,25(3):299-326.

[13] WITHERSPOON P A,WANG J S Y,IWAI K,et al.Validity of cubic law for fluid flow in a deformable rock fracture[J].Water Resources Research,1980,16(6):1016-1024.

[14] WARPINSKI N R,OTHERS.Investigation of the accuracy and reliability of in situ stress measurements using hydraulic fracturing in perforated cased holes[C]∥ARMA-83-0773 presented at the 24th US Symposium on Rock Mechanics (USRMS).Texas:American Rock Mechanics Association,1983.

[15] HOSSAIN M M,RAHMAN M K,RAHMAN S S.A comprehensive monograph for hydraulic fracture initiation from deviated wellbores under arbitrary stress regimes[R].SPE 54360,1999.

[16] 陈勉,庞飞,金衍.大尺寸真三轴水力压裂模拟与分析[J].岩石力学与工程学报,2000,19(增刊1):868-872.CHEN Mian,PANG Fei,JIN Yan.Experiments and analysis on hydraulic fracturing by a large-size triaxial simulator[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(S1):868-872.

[17] 柳贡慧,庞飞,陈治喜.水力压裂模拟实验中的相似准则[J].石油大学学报(自然科学版),2000,24(5):45-48.LIU Gonghui,PANG Fei,CHEN Zhixi.Development of scaling laws for hydraulic fracture simulation tests[J].Journal of the University of Petroleum,China(Edition of Natural Science),2000,24(5):45-48.

[18] VEEKEN C,DAVIES D R,WALTERS J V,et al.Limited communication between hydraulic fracture and (deviated) wellbore[R].SPE 18982,1989.

[19] Van KETTERIJ R G,PATER C J D.Impact of perforations on hydraulic fracture tortuosity[J].SPE Production & Facilities,1999,14(2):117-130.

[20] ABASS H H,HEDAYATI S,MEADOWS D L,et al.Nonplanar fracture propagation from a horizontal wellbore:experimental study[J].SPE Production & Facilities,1996,11(3):133-137.

[21] DANESHY A A.A study of inclined hydraulic fractures[J].Society of Petroleum Engineers Journal,1973,13(2):61-68.

[22] DANESHY A A.True and apparent direction of hydraulic fractures[R].SPE 3226,1971.

(编辑：孙丰成)

Finite element simulation of fracture initiation from multiple perforation channels of spiral pattern

SHAN Qinglin1JIN Yan1WANG Yajun2ZHANG Xiang2ZHANG Ruxin1WU Yue1LOU Erbiao3ZHOU Huabo4

(1.StateKeyLaboratoryofPetroleumResourcesandEngineering,ChinaUniversityofPetroleum,Beijing102249,China;2.PetroChinaChangqingOilfieldCompany,Xi’an,Shaanxi710016,China; 3.PetroChinaTarimOilfieldCompany,Korla,Xinjiang841000,China; 4.CNPCBohaiDrillingEngineeringCo.,Ltd.,Tianjin300457,China)

The accurate simulation of the fracture initiation around perforation channels can help guide the optimization of perforation design when spiral perforation is used.A finite element model (FEM) has been developed based on the flow-stress coupling theory to simulate the fracture initiation around perforation channels.A damage variable was employed in the model to describe the changes in stiffness, strength and permeability of the rock material, in order to track the initiation and propagation of the hydraulic fractures from the perforation channels and the wellbore.The simulation result shows that two patterns of the hydraulic fractures can be observed to occur successively with the increasing bottom-hole pressure (BHP) with the damage-coupled FEM model (D-FEM), which are the fractures propagating along the borehole wall and those propagating along the perforation axis.In addition, the initial hydraulic fractures of perforation channels for various wellbore orientations have also been investigated based on the D-FEM.By analyzing the hydraulic communication possibility and propagation trends of different initial fractures, the pattern of near-wellbore hydraulic fractures can be predicted.A set of physical simulation experiments has been performed, proving the validity of the D-FEM model.This model can be used to analyze the hydraulic fracture complexity in the near-wellbore region and provide guidance to field operations.

spiral perforation; finite element model; damage variable; near-wellbore hydraulic fracture; physical simulation experiment

*国家杰出青年科学基金项目“石油工程岩石力学(编号：51325402)”、国家自然科学基金重大项目“页岩油气高效开发基础理论研究(编号：51490651)”、国家自然科学基金重点项目“页岩气开采岩石力学(编号：51234006)”部分研究成果。

单清林，男，中国石油大学(北京)油气井工程专业在读博士研究生，主要从事石油工程岩石力学方面研究。地址：北京市昌平区府学路18号 中国石油大学(北京) 中油大厦 903室(邮编：102249)。E-mail：shanqinglin2000@163.com。

金衍,男，教授，博士生导师，主要从事油气井岩石力学与工程方面的研究。地址：北京市昌平区府学路18号中国石油大学(北京)石油工程学院(邮编：102249)。E-mail:jinyan_cup@163.com。

1673-1506(2017)04-0123-08

10.11935/j.issn.1673-1506.2017.04.016

TE257+.1

A

2017-03-10 改回日期：2017-04-03