平面五杆并联机器人滑模控制

刘新乐，唐予军，王 霞,2

（1.河北大学 电子信息工程学院，保定 071002；2.河北省数字医疗重点实验室，保定 071002）

平面五杆并联机器人滑模控制

刘新乐1，唐予军1，王 霞1,2

（1.河北大学 电子信息工程学院，保定 071002；2.河北省数字医疗重点实验室，保定 071002）

本文基于平面五连杆机器人的动力学模型, 把滑模控制理论应用于平面五连杆机器人的轨迹控制,为五连杆机器人设计轨迹跟踪滑模控制器。给出了驱动力矩的控制表达式，并证明了系统的渐近跟踪性能。对五连杆机器人进行Matlab/Simulink仿真，结果表明该方法能够使跟踪误差趋于0。

滑模控制；平面五连杆机构；Matlab/simulink

0 引言

平面并联机构是一种典型的并联机构，利用它可以综合出许多性能优良的机构，同时它也是研究空间并联机构的基础，最具代表性的平面并联机构是平面二自由度机构和平面三自由度机构。平面五杆机构是一种单闭环机构，具有结构简单、便于应用的特点，在不少领域中得到应用.它不仅可以作为机器人的本体结构，还可以作为机器人的部件使用，如作为步行机器人的步行机构，因此该机构得到了国内外许多学者的重视[1]。国内外关于并联机器人的研究主要集中于机构学、运动学、动力学和控制策略研究等几个领域。动力学主要研究驱动器作用在并联机构关节上的力或力矩与其产生的运动之间的关系，是进行并联机构运动控制和动态特性研究的基础。并联机器人在许多方面有十分重要的应用，如航天航海、机电工业、医疗器械、微型微动机械等[11]。但是，并联机器人作为一个结构复杂、多变量、多自由度、多参数耦合的非线性系统,其控制策略、控制方法的研究及其复杂。最初设计控制系统时，大多把并联机器人的各个分支当作完全独立的系统来进行控制，控制策略为传统的PID控制，控制效果很不理想。模糊控制方法可以在不要求机器人模型精确的情况下来实现机器人的控制，但是模糊控制方法的模糊规则设计比较重要，规则设计的好坏将会直接影响到控制的效果[2～4]，而且该规则的设计需要具有专家知识或是经过多次试验得到，因此在没有相应的条件下，该方法可能无法起到较好的控制效果。

滑模控制其本质上是一类特殊的非线性控制，其非线性表现为控制的不连续性。由于滑动模态可以进行设计且与对象参数及扰动无关，这就使得滑模控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点[3]。这种控制方法通过控制量的切换使系统状态沿着滑模面滑动，使系统在受到参数摄动和外干扰的时候具有不变性，正是这种特性使得滑模控制方法在机器人控制中得到广泛的应用[14]。

本文主要把滑模控制理论应用于平面五连杆机器人的轨迹控制，滑模控制系统主要目的是通过给定各关节的驱动力矩，使得机器人的位置能够跟踪给定的理想轨迹，从而保证关节位置的稳态误差为零。文中利用MATLAB/Simulink对机器人运动学进行仿真[11]。仿真结果表明，该方法对并联机器人消除位置稳态误差具有良好的控制效果。

1 问题描述

1.1 平面五连杆并联机器人的动力学模型

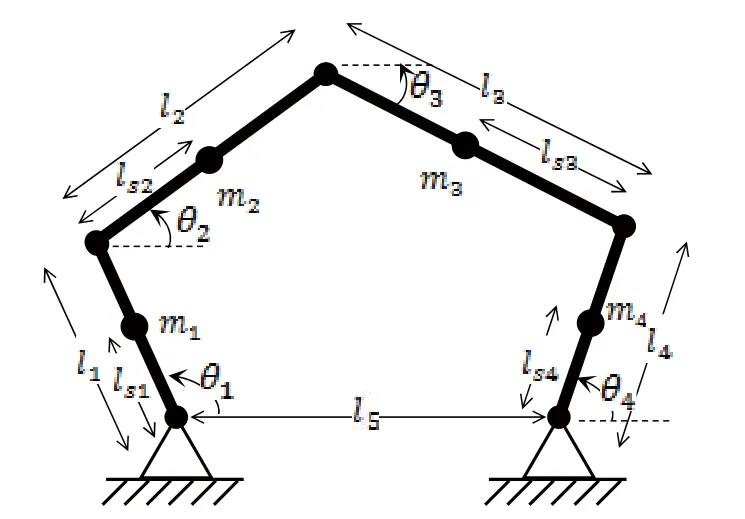
图1 平面五连杆的机构示意图

平面五连杆机构如图1所示，它由4个自由连杆和一个固定连杆组成。各个杆件长度分别为为各个连杆的质量，各杆件的质心位置位于图示处。各个连杆与轴x正向的夹角分别为，其中为主动角，为从动角，由决定：

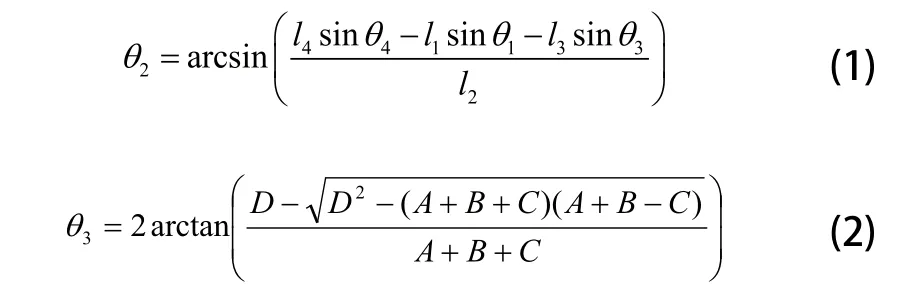
拉格朗日法求得平面五连杆并联机器人的动力学模型为[5.6]：

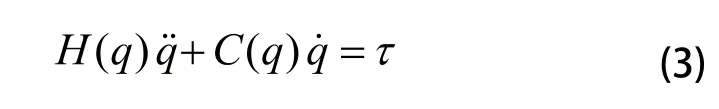
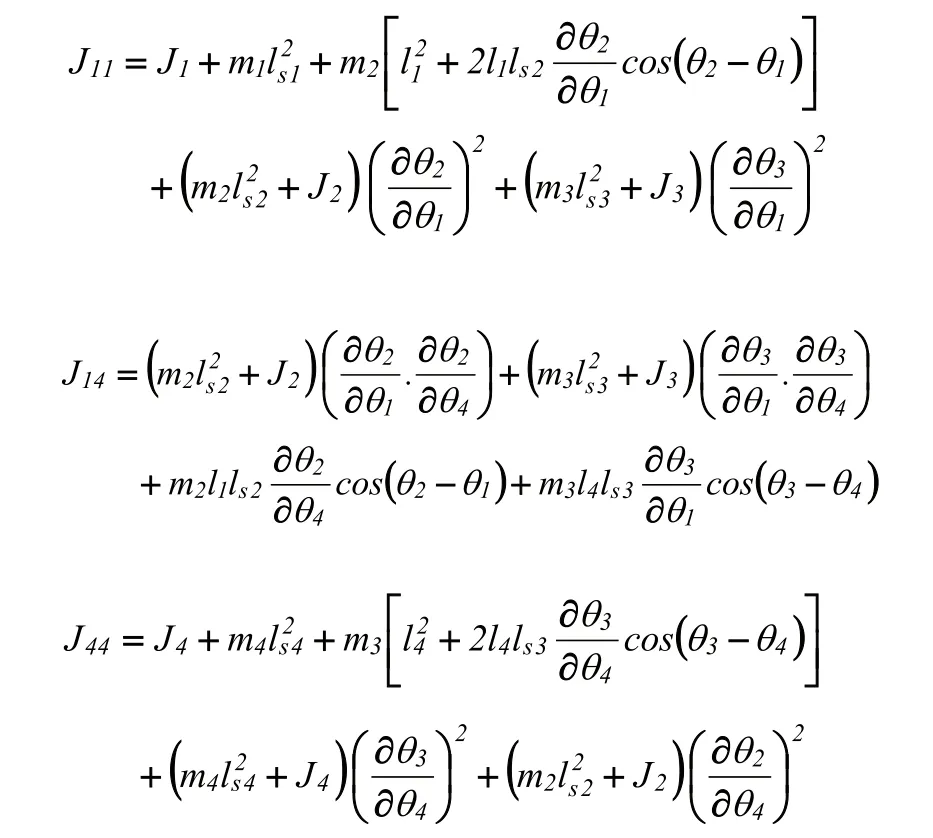
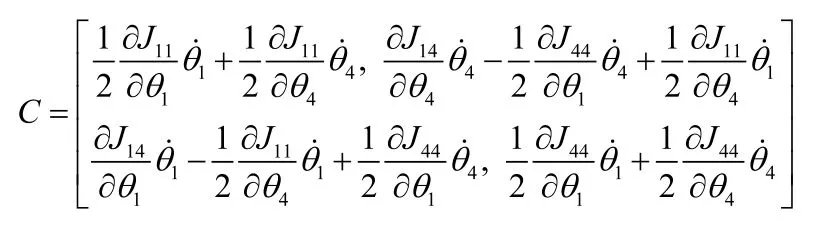
本文将会用到以下性质[4,6]：

性质1：(q)是正定矩阵，对任意的x满足：

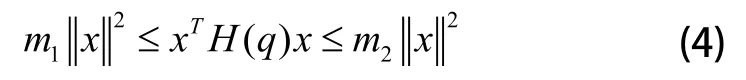
其中，m1和m2都是正的常数。

性质3：根据机器人动力学方程的线性特性：

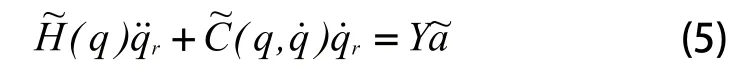
控制目标是为平面五连杆并联机器人设计滑模控制器，使得关节轨迹q能够渐近跟踪期望轨迹qd，也就是在该控制器作用下，跟踪误差~在尽可能短时间内收敛到零。

2 主要结果

根据文献[4]的方法，可以针对连杆机构设计一个滑模跟踪控制器，定义滑模平面[7]：

其中， 是一个常数矩阵。

构造：

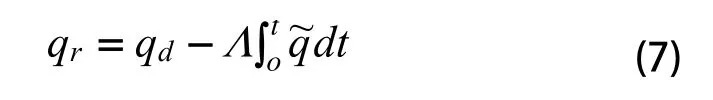
能够得到：

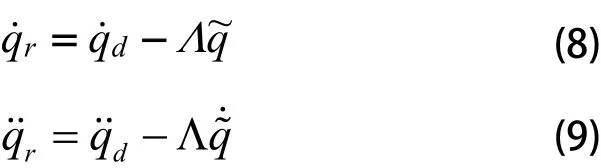
定义误差函数为：

该系统的滑模控制律为[10]：

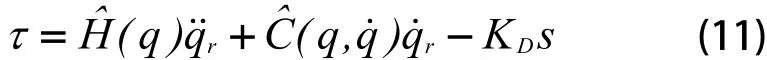
其中，KD是一个正定矩阵。

定理：针对平面五连杆并联机器人系统式(3)，如果采用控制律式(12)，则跟踪误差收敛于零。

证明：

构造Lyapunov函数：

对V求导数，得：

将式(11)带入(14)，得：

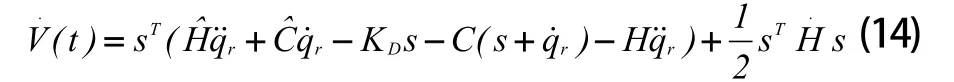
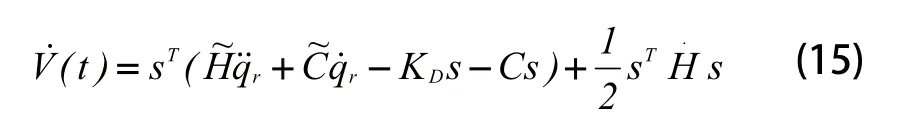
将式(6)带入式(16)，得：

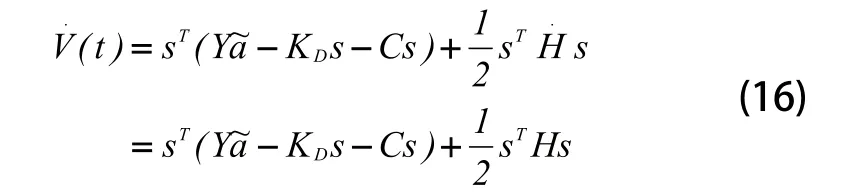
将式(2)带入式(17)，得：

3 仿真实例分析

为了证明滑模控制器的有效性和可行性，我们进行了平面五杆并联机器人的仿真实验。如表1给出了平面五杆并联机器人各杆件质量、各杆件质心位置和绕质心的转动惯量等特性参数：

对于系统(3)，使用滑模控制器(12)进行控制。关节的位置指令为滑模控制律中，取在Matlab/Simulink中搭建该控制器和五连杆的控制框图。

表1 平面五杆并联机器人参数

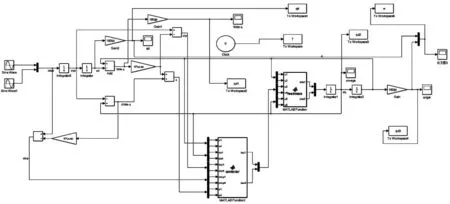
图2 平面五连杆滑模控制框图

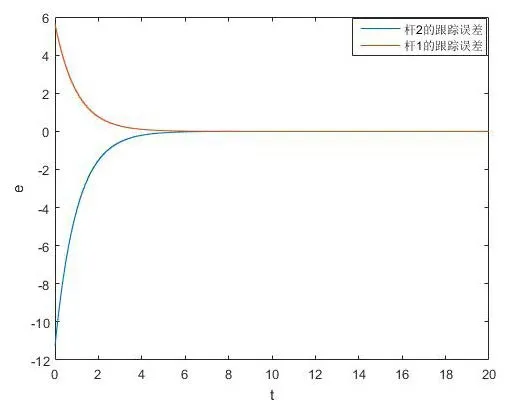
图3 跟踪误差

图4 角速度轨迹

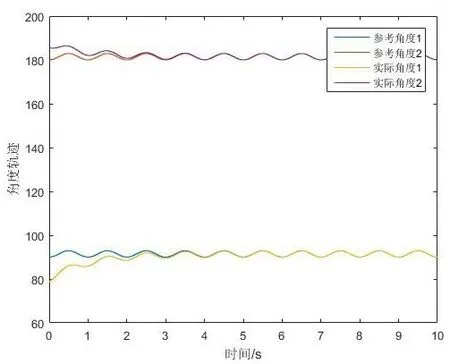
图5 角度轨迹

从图2中可以看出在短时间内关节的跟踪误差就能保持在很小的范围之内。图3为角速度运动轨迹，图4为角度轨迹，图像表明系统可以在很短的时间内跟踪上参考轨迹，并且能使稳态误差为零。

4 结论

本文针对平面五杆并联机器人的动力学模型设计了一种滑模控制策略,并进行了实验仿真。仿真结果显示，关节的实际运动轨迹可以快速的跟踪上指令轨迹，并使得后续跟踪误差被控制在很小的范围之内，从而保证了关节位置的稳态误差为零，验证了所设计控制器对于平面五杆并联机器人关节轨迹跟踪控制的有效性，提高了系统的控制性能。

[1] 陈美钰,辛洪兵.平面五杆并联机器人动力学分析[J].北京工商大学学报,2009,27(6):7-8.

[2] 牛雪梅,高国琴,鲍智达,等.基于滑模变结构控制的温室喷药移动机器人路径跟踪[J].农业工程学报,2013,29(2):11-13.

[3] 杨洁,王庆林,李原.滑模变结构研究综述[C].第三十一届中国控制会议,国际会议,2012.

[4] J. Liu. Design and MATLAB simulation of robot control system[M].Peking:Tsinghua University Press, 2008.

[5] T.L. Shen.Robust Conrrol of Robot Manipulators[M].Peking:Tsinghua,2000.

[6] 曹建斌,訾斌.混合驱动平面五连杆机构优化设计与迭代学习控制[J].机械传动,2011,35(6):2-3.

[7] 马千惠.多关节机器人的滑模控制策略研究[D].东北石油大学,2014.

[8] Chyi-Tsong chen. A Sliding Mode Control Strategy for Temperature Trajectory Tracking in Batch Processes[J].IFAC Proceedings Volumes, 2012,Vol.45(15).

[9] Petr Husek. Adaptive sliding mode Control with moving sliding surface [J].Applied Soft computing, 2016,Vol.42.

[10] 刘永慧.滑模变结构控制的研究综述[J].上海电机学院学报,2016,19(2):91-92.

[11] 王锡霖,严日明,李举,等.基于MATLAB的平面五连杆的运动学分析[C].第十三届沈阳科学学术年会,中国会议,2016.

[12] 杨博,吴伟.基于滑模变结构控制的轮式机器人控制系统设计仿真[J].长春工业大学学报(自然科学版),2011,32(3):273-274.

[13] 秋夷,王洪瑞.滑模变结构控制策略在机器人控制中的应用研究[D].燕山大学,2010.

[14] 姜寅令.滑模控制方法在机器人轨迹跟踪中的应用[D].东北石油大学,2011.

[15] 胡峰,骆德渊,雷霆,等.基于Simulink/SimMechanics的三自由度并联机器人控制系统仿真[J].自动化与仪器仪表,2012,27(5):221-223.

Simulation of sliding mode control for planar fi ve-bar parallel manipulator

LIU Xin-le1, TANG Yu-jun1, WANG Xia1,2

TP273

：A

：1009-0134(2017)08-0039-04

2017-06-21

国家自然科学基金（61403118，11271106）；河北省自然科学基金（F2015201088）；河北大学科研基金资助项目（2010Q04）；河北大学中西部提升综合实力——高层次创新人才培养和引进计划项目

唐予军 （1979 -），男，讲师，硕士，主要从事切换系统研究。