改进遗传算法PID参数优化在流浆箱总压控制中的应用
莫卫林 杨 浩 熊智新 胡慕伊
(南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037)
·流浆箱总压控制·
改进遗传算法PID参数优化在流浆箱总压控制中的应用
莫卫林 杨 浩 熊智新*胡慕伊
(南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037)
稀释水水力式流浆箱的总压控制直接关系到纸张质量的好坏,传统的PID方法对于非线性、参数时变性和模型不确定性的对象控制精度较低。虽然传统遗传算法可以优化PID参数,提高精度,但是收敛速度慢,整定时间长,限制其在高速纸机控制中的应用。针对这些问题,本课题以纸机流浆箱总压控制为研究对象,采用改进的遗传算法来整定PID参数,通过优化交叉和变异算子、增加当前最优追踪策略以及改进收敛准则等方法来提高遗传算法的全局寻优能力和收敛速度。仿真结果表明,用改进的遗传算法整定后的流浆箱总压控制PID具有更快的响应速度和更好的鲁棒性。
流浆箱总压;PID参数优化;改进遗传算法
(*E-mail: leo_xzx@njfu.edu.cn )
流浆箱被称为纸机的心脏,是连接备浆流送和纸张成形两部分的关键枢纽,随着纸机车速的提高,从流浆箱喷出浆料,再到网上定形的时间变得非常短,为了保证浆料分布均匀一致,其总压的控制就至关重要,决定着上浆流量和流速,也影响着纸张成形的质量[1-3]。
流浆箱的压力控制通常采用PID控制,然而在实际应用中,总压控制存在一定的非线性、参数时变性和模型不确定性,所以一般的PID控制难以实现总压的精确控制[4]。因此有很多文献[5-7]报道了采用现代优化算法来整定PID参数,并取得了较好的效果。其中遗传算法(Genetic Algorithms,GA)具有很强的全局搜索能力,通用性强,鲁棒性好,并已被证实基于遗传算法的控制器参数整定优于传统的整定方法,因而被广泛应用于很多领域[8-10]。其中在造纸过程控制方面,王艳华等人[11]在以往的CMAC与PID复合控制中引入遗传算法,实现了对纸浆蒸煮温度的优化控制;胡康等人[12]引入遗传算法对人工神经网络进行优化,可以实现对废水处理过程更有效的控制。但是,传统的遗传算法存在一定的不足,容易产生早熟收敛,同时收敛的速度较慢,搜索时间过长[13],所以将遗传算法用于造纸控制领域的研究并不多。近年来,国内外学者对遗传算法进行了各种各样的改进,总的来说主要有两个方面:一是改进自身基因的遗传算法[14],二是与其他算法相结合的混合遗传算法[15],但所有的改进都是为了克服“早熟”问题,提高遗传算法的全局寻优能力以及加快算法的收敛速度。
本课题对传统遗传算法的交叉算子、变异算子以及收敛准则进行改进,并增加了当前最优追踪策略,得到一种改进遗传算法,并针对稀释水水力式流浆箱总压PID控制器参数自整定模型进行仿真实验,通过和传统遗传算法以及Z-N整定法的仿真对比,以验证改进遗传算法的良好效果。
1 基本原理
1.1 流浆箱总压控制
流浆箱的主要任务是沿纸机幅宽方向均匀地分布浆料,同时保证速度、压力、浓度、流量、以及纤维定向等因素的稳定和均匀。本课题研究的满流式稀释水水力式流浆箱,其特点是可以根据纸机的车速情况,通过控制冲浆泵的输浆压力来调节浆料的上网速度[16]。这种流浆箱对应的纸机车速相对较高,并且它的液位和压力之间没有耦合关系,所以总压就变成影响纸张质量的最重要因素。总压控制着流浆箱的喷浆速度,它的稳定与否直接影响着纸张的纵向定量分布情况,因此必须保证总压控制回路在最佳工作状态。总压控制的示意图如图1所示。

图1 流浆箱总压控制结构图
稀释水水力式流浆箱通过PLC来控制冲浆泵的变频器实现总压控制。总压设定值直接在上位机给定,通过通信接口送给PLC。冲浆泵把浆料打到布浆系统的同时,对总压产生了很大的冲击,此时来自冲浆泵的浆料需要经过脉冲衰减作用稳定后,再以一定的流量从流浆箱喷射到网部。计算机根据总压的设定值和测量值,经过相应的处理后,给出4~20 mA的控制信号,通过变频器控制冲浆泵的转速[17]。
1.2 遗传算法简介
遗传算法(GA)最早由美国的J.H.Holland教授于1975年提出,是模仿生物进化过程而形成的一种自适应全局优化概率搜索算法。遗传算法的基本思想是把待优化参数进行编码(通常是二进制编码),然后由若干个位串形成初始种群作为待求问题的候选解,通过选择(select)、交叉(crossover)、变异(mutation)进行操作,不断迭代优化,直到满足最优为止。作为一种全局优化、并行搜索的寻优方法,遗传算法只依赖于适应度函数,即使在对象模型不确定的情况下,它仍可根据对象的输出情况进行优化,但简单遗传算法存在早熟问题,不能保证收敛于全局最优[5]。本课题探索用改进的遗传算法对PID参数进行整定。基本遗传算法的流程如图2所示。
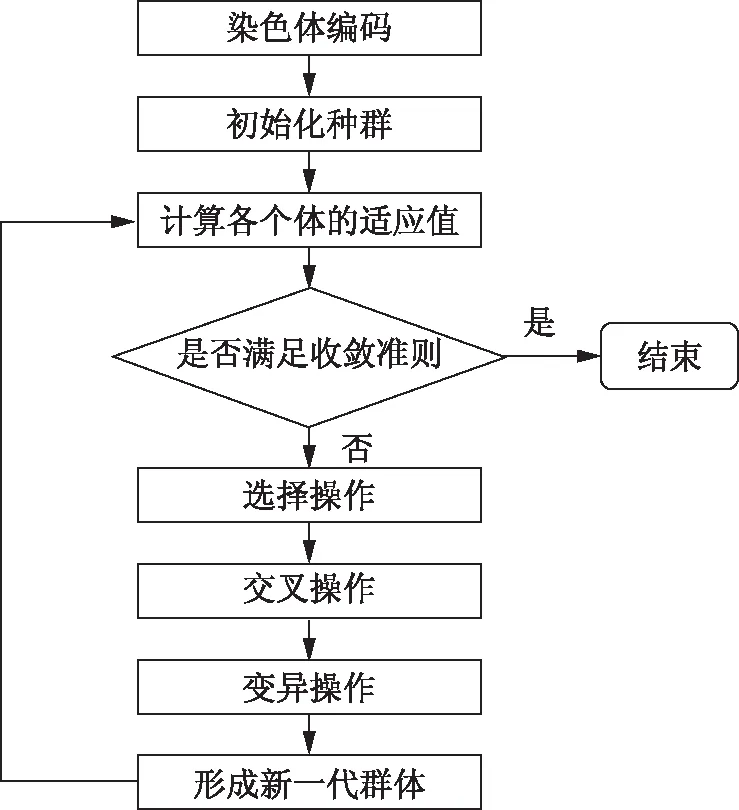
图2 基本遗传算法流程图
2 基于改进遗传算法PID参数整定
2.1 适应度函数的确定
利用遗传算法优化PID 参数的基本思想就是利用遗传算法较强的全局寻优能力,选出最佳Kp、Ki、Kd参数组合以使控制系统的某一性能指标达到最佳。现今常用的4种系统性能评价指标为:平方误差积分(ISE)、绝对误差积分(IAE)、时间乘平方误差积分( ISAE) 、时间和绝对误差乘积积分(ITAE)等[18]。考虑到要兼顾动态与静态性能,本课题选用 ITAE作为性能评价指标,ITAE值越小,PID整定效果越好,其定义为式(1)。
(1)
2.2 选择方法的改进
本课题结合文献[19]的方法,对遗传算法交叉算子,变异算子改进的同时,又增加了当前最优追踪策略,最后改进了收敛准则,从而使遗传算法在PID整定优化中获得更好的效果。
2.2.1 改进交叉算子
交叉操作是遗传算法与其他进化算法的重要区别,是产生新个体的主要途径。交叉算子既关系着遗传算法的收敛性,也对遗传算法的收敛速度有着关键的影响。传统的交叉概率通常取一个固定的值,然而在进化初期,需要扩大父代之间的交叉操作来增强群体的多样性,而在进化后期,群体逐渐搜寻到最优解附近,这时,如果再继续采用大的交叉率,则会产生很多发散分布在搜索空间的新个体,反而会破坏原先优良个体所占的比例,延缓收敛。因此,本课题采用式(2)来确定交叉概率的值。
Pc=Pc0-(Pc0-Pcmin)·d/D
(2)
式中,Pc0是初始交叉率;Pcmin是允许的最小交叉率值;d代表当前进化次数;D代表总的进化次数。
2.2.2 改进变异算子
变异操作是指将个体染色体的某些基因位进行改变,是增大种群多样性的另一重要途径。在设计变异算子时,有以下几点需要注意:
(1)要在其允许的范围内进行基因变异,保证突变个体满足约束条件。
(2)在进化前期希望加大变异率,使新个体能够在整个搜索空间迅速扩散,而在进化后期靠近最优解时,又希望降低变异率,防止父代中优良基因的丢失,以加快收敛进程。
(3)在群体平均适应值较差时,应加大突变量,以增强产生优良个体的概率,而在群体平均适应值到达最优解附近时,则应该减少突变量。综合以上因素,本课题采用式(3)作为自适应变异率值。
(3)

2.2.3 增加当前最优追踪策略
通过改进遗传算法内部交叉和变异算子,可以增加种群的多样性,从而更快找到最优解,然而一定程度上也破坏了优良种群。采用当前最优追踪策略,通过保存每一代的当前最优解,可以对每次进化的结果进行修正,避免优良基因的丢失。
2.2.4 改进收敛准则
通常遗传算法采用总的进化次数D为收敛依据,当进化次数达到D,就终止程序。然而,在算法运行过程中,如果初始种群以及其他参数选取非常理想时,那么遗传算法可能很快就寻找到最优解。这时,如果继续采用总进化次数D为收敛准则,即便已经找到最优解,也要继续进化操作直到运行完总进化次数,这样就增加了不必要的运算时间。
根据以上增加的当前最优追踪策略,记录每代的最优Kp、Ki、Kd参数,构成三维决策向量V,为了研究决策向量在迭代过程中的收敛性,引进范数的概念[20]。通过相邻向量差的范数‖ΔV‖2可以反映决策向量V在每次迭代时的变化情况,有‖ΔV‖2=‖Vj+1-Vj‖2,其中Vj和Vj+1分别表示第j代和第j+1代的决策向量,这里笔者采用2-范数,即欧式范数。
因此,在算法运行过程中,笔者采用双重收敛准则。
(1)总的进化次数D。
(2)相邻决策向量差的范数‖ΔV‖2连续15代进化结果小于某一提前设定值。
在遗传进化过程中,只要满足上述其中一个条件,都判定满足收敛条件。这种双重收敛约束可以适当减少不必要的运算时间。
2.3 遗传算法优化流浆箱PID参数
在流浆箱总压PID控制系统中,要确定的是Kp、Ki、Kd这3个参数。采用遗传算法进行参数调节,其中种群的适应度值对应控制系统的性能指标ITAE。首先由遗传算法产生初始种群,并将种群信息赋予PID参数,然后根据适应度函数计算每一组参数的适应度值,接着对种群进行遗传操作,不断进化,直到找到群体中的最优个体,输出PID控制器的最优参数。优化过程如图3所示。
遗传算法优化PID的流程如下。
(1)编码。采用二进制编码,对Kp、Ki和Kd这3个参数进行编码,即成为一条染色体。
(2)初始化群体生成。作为进化初始种群,根据设置的群体大小而随机产生。
(3)遗传参数的确定。遗传算法在寻优时不需要外部信息,但是需要确定群体规模,初始变异概率,最小变异概率,初始交叉概率,最小交叉概率以及选择概率。
(4)计算个体适应度值。按照式(1)定义的适应度函数来对群体中的每个个体计算适应度值,并找出这一代的最优种群和最优值。
(5)进行遗传操作。进行选择、改进交叉和改进变异操作,产生新的种群。
(6)计算新种群的适应度值(如步骤4)。若满足收敛条件,则输出最优PID参数,否则,重新回到步骤(5),进行新的遗传操作,直到满足终止条件。

图3 遗传算法优化PID的过程示意图
3 仿真实验与分析
本课题运用MATLAB中的Simulink进行仿真实验,根据文献[17,21]所述,对稀释水水力式流浆箱总压控制系统,采取简化一阶惯性加延时的环节,通过阶跃响应作图法来获取其数学模型为式(4)。
(4)
下面采用Z-N整定法、传统遗传算法、改进遗传算法等3种方法来对PID参数进行整定仿真对比实验。其中Kp、Ki、Kd这3个待优化参数的取值范围为[0,10]。两种遗传算法中,种群规模均设为100,最大迭代次数均为100次。传统遗传算法中,Pc0=0.7,Pm0=0.1,改进遗传算法中,另外引进Pcmin=0.4,Pmmin=0.001。3种方法整定后的参数及性能指标如表1所示。
图4为ITAE指标在两种遗传算法分别整定下的优化曲线。对比两条曲线可以看出,两种算法最后优化的指标值几乎一致,虽然传统遗传算法在第40代已经接近最优,但收敛极慢,直到进化至第98代才达最优,而改进遗传算法在第13代已经接近最优,在第 53 代就达到了最优,表明改进遗传算法的收敛速度大大提高。PID参数在优化过程中的变化曲线如图5所示。
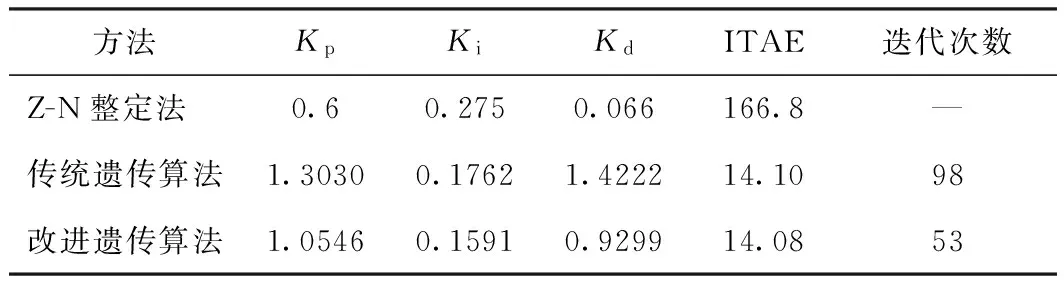
表1 3种方法整定后的PID参数和性能指标

图4 两种遗传算法优化的指标变化曲线

图5 改进遗传算法的Kp、Ki、Kd优化曲线
图6为相邻决策向量差的范数‖ΔV‖2在改进遗传算法优化过程中的变化曲线。从图5中可以看出,Kp、Ki、Kd3个参数在第13代时基本趋于稳定,而图6也更直观地显示出,当进化到第13代时,范数‖ΔV‖2开始接近于0,并从第53代开始恒等于0,代表决策向量V不再变化,满足了提前收敛的条件,可以提前终止程序,说明改进遗传算法有效减少了运算时间。

图6 范数‖ΔV‖2在改进遗传算法中的变化曲线

图7 不同方法所对应的单位阶跃响应曲线
图7为在总仿真时间为120 s下的不同方法整定曲线,由图7可知,经两种遗传算法优化后的PID模型,在调节时间和超调量上都得到了很大的改善;而改进遗传算法优化的比传统遗传算法优化的调节时间缩短了7.5 s,响应速度更快,总运行时间上减少了30 s,而且几乎无超调,显然改进遗传算法能够更有效地优化出较好的参数,并且减少了运算时间,可以有效地解决PID控制器参数整定难的问题。
在实际的控制过程中,流浆箱压力的数学模型会受干扰、噪声和非线性等因素的影响而发生变化[22]。假设模型失配时的传递函数为式(5)。
(5)
采用上述调整好的仿真模型来对此时模型失配的情况进行仿真,并在第100 s时给系统加入30%的干扰。图8为在Z-N整定法、传统遗传算法以及改进遗传算法优化下的响应曲线。从图8中可以看出,当模型参数发生变化以及出现较大干扰时,3种控制方法的控制效果都比模型匹配时要减弱。但是两种遗传算法都比Z-N整定法具有更强的鲁棒性,并且改进遗传算法比传统遗传算法响应速度要更快。

图8 模型失配时的阶跃响应曲线
4 结 论
通过对遗传算法的改进,既保证了前期遗传算法种群的多样化和进化质量,也提升了后期遗传算法的收敛速度,并减少了整个算法的运行时间。MATLAB仿真结果表明,改进遗传算法优化的PID比传统方法优化的控制精度更高;比传统遗传算法的收敛速度更快,运算时间更少,系统鲁棒性也更好。说明这种改进遗传算法能有效提高流浆箱总压PID控制系统的动态特性和稳态特性,这对于提高造纸生产中高速流浆箱的总压控制质量有一定的理论指导意义。
[1] CHEN Hang, TANG Wei, LIU Wen-bo, et al. Structure and Control of a Hydraulic Headbox with Dilution Water[J]. China Pulp & Paper, 2013, 32(12): 38. 陈 航, 汤 伟, 刘文波, 等. 稀释水水力式流浆箱结构与控制[J]. 中国造纸, 2013, 32(12): 38.
[2] TANG Wei, WANG Meng-xiao, LI Ming-hui. A Survey on the Development of Headbox[J]. Journal of Shaanxi University of Science & Technology, 2005, 23(5): 132. 汤 伟, 王孟效, 李明辉. 纸机流浆箱的发展综述[J]. 陕西科技大学学报, 2005, 23(5): 132.
[3] LIN Mei-chan. Research & Development of the Key Technology of MC Dilution Hydraulic Headbox[J]. China Pulp & Paper, 2010, 29(3): 56. 林美婵. MC稀释水型水力式流浆箱关键技术的开发[J] . 中国造纸, 2010, 29(3): 56.
[4] YU Hai-bo. Application of Fuzzy PID in Air-cushioned Headbox Control System [J]. China Pulp & Paper, 2015, 34(9): 55. 于海波. 模糊PID在气垫式流浆箱控制系统中的应用[J]. 中国造纸, 2015, 34(9): 55.
[5] NIU Xiang-jie, WANG Yu-jie, TANG Jian. Optimization Parameters of PID Controller Parameters Based on Genetic Algorithm[J]. Computer Simulation, 2010, 27(11): 180. 牛芗洁, 王玉洁, 唐 剑. 基于遗传算法的PID控制器参数优化研究[J]. 计算机仿真, 2010, 27(11): 180.
[6] ZHANG Jia-jun. Optimization Parameters of PID Controller Parameters Based on Particle Swarm Optimization[J]. Computer Simulation, 2010, 27(10): 191. 张家骏. 基于粒子群算法的PID控制器参数优化研究[J]. 计算机仿真, 2010, 27(10): 191.
[7] Li Ling-yu, Guo Gui-fa, Xu Jin-biao. Optimizing and Adjusting the Parameter of PID Based on Simulated Annealing Genetic Algorithms[J]. Journal of Guangdong University of Technology, 2010, 27(2): 80. 李凌宇, 郭贵法, 许锦标. 基于模拟退火遗传算法的PID参数整定与优化[J]. 广东工业大学学报, 2010, 27(2): 80.
[8] Yuan Man, Liu Yaolin. Land use optimization allocation based on multi-agent genetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(1): 191. 袁 满, 刘耀林. 基于多智能体遗传算法的土地利用优化配置[J]. 农业工程学报, 2014, 30(1): 191.
[9] LI Liyi, TANG Yongbin, LIU Jiaxi, et al. Application of the Multiple Population Genetic Algorithm in Optimum Design of Air-core Permanent Magnet Linear Synchronous Motors [J]. Proceedings of the CSEE, 2013, 33(15): 69. 李立毅, 唐勇斌, 刘家曦, 等. 多种群遗传算法在无铁心永磁直线同步电机优化设计中的应用[J]. 中国电机工程学报, 2013, 33(15): 69.
[10] LI Hui, WANG He-sheng, SHI Xu-yang, et al. Study on equivalent model of wind farms based on genetic algorithm[J]. Power System Protection and Control, 2011, 39(11): 1. 李 辉, 王荷生, 史旭阳, 等. 基于遗传算法的风电场等值模型的研究[J]. 电力系统保护与控制, 2011, 39(11): 1.
[11] WANG Yanhua, WANG Zhi, DING Jianjun. Application of CMAC and PID Com Pound Control Based on Genetic Algorithm for Pulp-Cooking Heating Control[J]. Microcomputer Information Journal, 2007, 23(4): 48. 王艳华, 王 直, 丁建军. 遗传算法复合控制在纸浆蒸煮中的应用[J]. 微计算机信息, 2007, 23(4): 48.
[12] HU Kang, WAN Jin-quan. Intelligent Control System Based on Genetic Neural Network for Wastewater Treatment[J]. Computer Technology and Development, 2011, 21(2): 18. 胡 康, 万金泉. 基于遗传算法的控制系统在废水处理中的应用[J]. 计算机技术与发展, 2011, 21(2): 18.
[13] ZHANG Wei, LU Yu-qing. Optimized and Adjust the Parameter of PID Based on On-line Adaptive Genetic Algorithms[J]. Computer Simulation, 2011, 28(12): 154. 张 巍, 卢宇清. 基于在线自适应遗传算法的PID参数整定和优化[J]. 计算机仿真, 2011, 28(12): 154.
[14] LEE C H, CHANG F K. Fractional-order PID Controller Optimization via Improved Electromagnetism-like Algorithm[J]. Expert Systems with Applications, 2010, 37(12): 8871.
[15] WANG Xian-fang, DU Zhi-yong, PAN Feng. Tuning PID parameters based on chaotic immune genetic algorithms[J]. Computer Engineering and Applications, 2010, 46(13): 242. 王鲜芳, 杜志勇, 潘 丰. 基于混沌免疫遗传算法整定PID参数[J]. 计算机工程与应用, 2010, 46(13): 242.
[16] LU Qian-he. Papermaking principles and Engineering[M]. Beijing: China Light Industry Press, 2006. 卢谦和. 造纸原理与工程[M]. 北京: 中国轻工业出版社, 2006.
[17] NIU Xu-zhong. Research and Implementation of Dilution Hydraulic Headbox Ontology Control System[D]. Xi’an: Shaanxi University of Science & Technology, 2012. 牛绪钟. 稀释水水力式流浆箱本体控制系统的研究与实现[D]. 西安: 陕西科技大学, 2012.
[18] ZENG Cheng, ZHAO Xi-jun. Application of improved quantum genetic algorithm in PID parameter tuning[J]. Electric Power Automation Equipment, 2009, 29(10): 125. 曾 成, 赵锡均. 改进量子遗传算法在PID参数整定中应用[J]. 电力自动化设备, 2009, 29(10): 125.
[19] Cui Shanshan. Some Improvements of the Genetic Algorithm and Their Applications[D]. Hefei: University of Science and Technology of China, 2010. 崔珊珊. 遗传算法的一些改进及其应用[D]. 合肥: 中国科学技术大学, 2010.
[20] Li Qing-yang. Numerical Analysis[M]. Beijing: Tsinghua University Press, 2012. 李庆扬. 数值分析[M]. 北京: 清华大学出版社, 2012.
[21] CHEN Shuai-shuai, ZHAO Qian-mei, XIONG Zhi-xin, et al. Application of the PID Parameters Self-tuning Based on IPSO in Headbox Total Pressure Control[J]. China Pulp & Paper, 2015, 34(11): 37. 陈帅帅, 赵倩梅, 熊智新, 等. 基于IPSO的PID参数自整定在流浆箱总压控制中的应用[J]. 中国造纸, 2015, 34(11): 37.

(责任编辑:常 青)
Application of the PID Parameters Optimization Based on Improved Genetic Algorithm in Total Pressure Control of Headbox
MO Wei-lin YANG Hao XIONG Zhi-xin*HU Mu-yi
(JiangsuProvincialKeyLabofPulpandPaperScienceandTechnology,NanjingForestryUniversity,Nanjing,JiangsuProvince, 210037)
The total pressure control of the diluted water hydraulic headbox is directly related to the quality of the paper. The traditional PID method has low control precision for the object which is nonlinear, parameter time-varying and model uncertainty. Although the traditional genetic algorithm can optimize the PID parameters and improve the precision, it has a slow convergence speed and a long dynamic response time, which limit its application in the control of high speed paper machine. Aiming at these problems, an improved genetic algorithm, which optimize the operators of crossover and mutation, take the optimal tracking strategy and inprove convergence criterion to enhance theorenall optimization ability of genetic algorithm and speed up the convergence rate, was employed in this paper to tune the PID parameters in total pressure control of headbox of the paper-making machine. The simulation results showed that the proposed method had faster response speed and better robustness than the Z-N tuning and traditional genetic algorithm.
total pressure of headbox; PID parameter optimization; improved genetic algorithm
莫卫林先生,在读硕士研究生;主要研究方向:制浆造纸过程控制与信息智能处理。
2017- 03- 28(修改稿)
国家林业局948项目“农林剩余物制机械浆节能和减量技术引进” (2014- 4-3)。
TS736
A
10.11980/j.issn.0254- 508X.2017.08.007
*通信作者:熊智新,博士,副教授;主要从事过程控制和信息智能处理方面的研究。

