基于部分线性回归的红外光谱多元校正方法

郭露，彭江涛，付辉敬

(湖北大学数学与统计学学院, 湖北 武汉 430062)

基于部分线性回归的红外光谱多元校正方法

郭露，彭江涛，付辉敬

(湖北大学数学与统计学学院, 湖北 武汉 430062)

对于红外光谱数据而言，光谱-浓度关系常表现为一种复杂的混合线性关系. 本文中提出一种部分线性回归算法，将复杂的光谱-浓度目标回归函数分解为线性和非线性决策函数之和. 具体地，采用一序列的线性和非线性核函数来构建回归模型，分别用于逼近目标函数中的线性和非线性成分. 本文中所提出的的方法与偏最小二乘回归算法和正则化最小二乘回归算法在3个实例数据集上进行实验对比.实验结果表明，本文中提出的算法具有更高的预测精度.

部分线性回归; 红外光谱; 多元校正

多元校正是化学计量学中的一个非常有力的工具.多元校正能够在光谱和对应的浓度之间建立一个回归模型，揭示物质成分之间的定量关系.传统的多元校正通常假定回归模型是呈线性关系的，例如多元线性回归(MLR)、 主成分回归(PCR)以及偏最小二乘回归(PLS)[1-3].在这些方法中，PLS在化学计量学中的应用最为广泛.

PLS将高维预测变量投射到低维的、不相关的潜在变量集合中，并要求潜在变量与响应之间有最大的协方差.当变量数量远超过样本数量或者数据中存在共线性预测变量时，PLS是非常有效的方法[1-3]. 然而，当数据表现出很强的非线性特征时，传统的线性PLS方法不能完全描述光谱与相应的浓度之间的关系，因而会产生较大的误差.

为了更好地描述光谱和浓度之间的非线性关系，正则化最小二乘回归算法(RLS)[4]用核函数来表示决策函数. 由于核函数可完全由训练集中的输入样本决定，选择一个合适的非线性核(例如高斯径向基核)，RLS就能很好地实现非线性回归.但是，单核RLS的能力是非常有限的，对于复杂的非线性光谱数据，单核RLS并不适用.如果回归函数由多种不同成分组成，例如，既包含线性成分又含有非线性成分，既包含平坦成分又包含陡变成分，此时RLS会造成过拟合或者欠拟合现象.因此，采用多种不同类型的核函数组会比单核更加有效，线性核和非线性核分别能够处理目标函数中的线性部分和非线性部分.

在本文中，我们提出一种部分线性回归算法(PLR)，用于多元校正.在PLR 中，目标回归函数表示为线性和非线性核决策函数的和，每个核函数能够逼近目标函数中的不同成分.

1 算法

学习理论中回归问题的目的是从样本中学习到回归函数或者得到其好的逼近.在最小二乘回归问题中，寻找回归函数的最小二乘正则化算法是与Mercer核K相联系的. 设K:X×X→R是一连续、对称且正定的函数，称为Mercer核[5].由核K生成的再生核希尔伯特空间HK定义为由函数集{Kx:=K(x,·):x∈X}所张成的闭包，其中内积〈·,·〉HK=〈·,·〉K定义为〈Kx,Kx′〉K=K(x,x′)，再生性表现为

〈Kx,Kx′〉K=K(x,x′)

(1)

与Mercer核K相联系的回归问题的最小二乘正则化算法定义为：根据一个训练样本集z={(x1,y1),(x2,y2),…,(xn,yn)}，寻找与z相关联的最小二乘优化问题的最小化函数：

(2)

其中，λ≥0是正则项参数.根据表示理论[6]，问题(2)的解可表示为：

(3)

同时，α=(α1,…,αn)T也是适定线性问题(4)的唯一解.

(nλI+K[x])α=y

(4)

在(4)式中，K[x]是n×n的矩阵，第(i,j)个元素为K(xi,xj)，以及y=(y1,y2,…,yn)T. 问题(2)的正则项满足

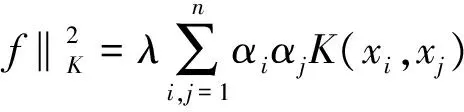
(5)

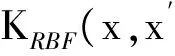
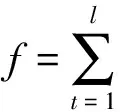
(6)

(7)

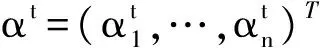
(8)

在(8)式中，Kt[x]是n×n的矩阵，第(i,j) 个元素为Kt(xi,xj)，以及y=(y1,y2,…,yn)T.

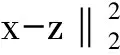
(24)

2 实验

2.1 数据集 选取3个公共数据集来进行测试分析.

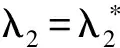
对于不同算法，均采用均方误差根(RMSEP)来衡量其预测性能.RMSEP衡量测试集样本的预测值与实际值之间的差异程度，定义为：

(25)

3 结果分析

3.1Corn数据集Corn数据集包含水分、油脂、蛋白质和淀粉这4种成分的校正问题.对训练数据进行数据归一化，采取交叉验证的方法对各个算法寻找最优参数，得到的最优参数结果见表(1)中的第一行.利用最优参数建立回归模型，代入测试数据得到预测结果见表(2).结果显示，对于Corn数据集4种成分，PLR方法预测结果的均方误差RESEP均低于PLS和RLS. 总体而言，PLR算法的预测能力更强.

表1 不同算法的最优参数——不同数据集

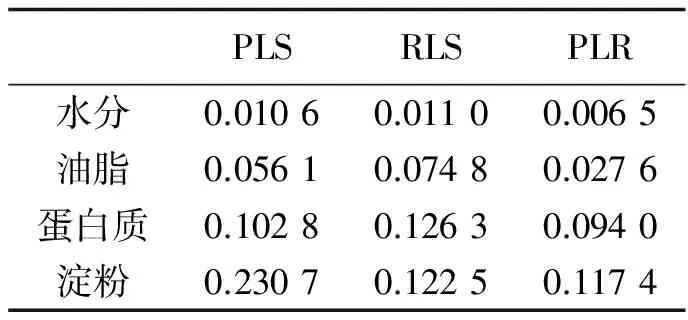
表2 不同算法的预测结果——Corn

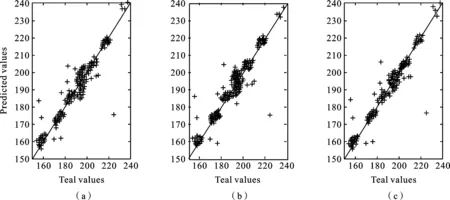
图1 真实值与预测值的对比图

3.2 Tablet 2002数据集 对训练数据进行数据归一化，采取交叉验证的方法对各个算法寻找最优参数，得到的最优参数结果见表(1)中的第二行.利用最优参数建立回归模型，代入测试数据得到预测结果.3种方法预测结果的均方误差分别为4.693 7、4.581 3和4.126 5. 可以看出，本文中算法可使预测精度得到提高，性能优于PLS 和RLS算法. 为了更好地看出各个算法的拟合效果，图1中显示各算法的预测

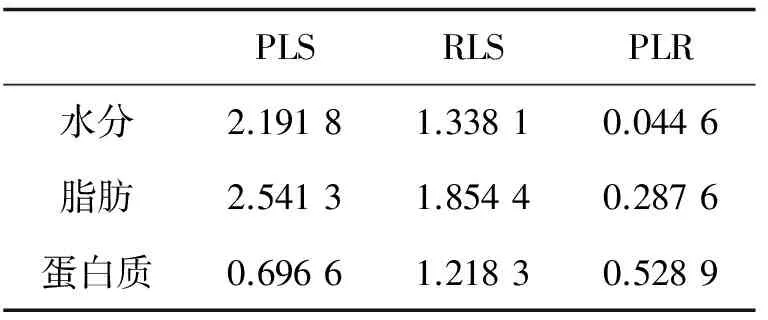
表3 不同算法的预测结果——Meat

值与真实浓度值之间的拟合效果图.从图中可以看出， PLR算法具有更好的拟合精度.

3.3 Meat数据集 同样地，Meat数据集的最优参数结果见表1中的最后一行.利用最优参数建立回归模型，针对测试数据得到预测结果见表3.从结果可以看出，对于水分、脂肪、和蛋白质这3 种成分，PLR方法的预测结果均优于PLS和RLS.

4 结论

针对复杂光谱数据的多元校正问题，本文中提出一种部分线性回归算法(PLR)，其决策函数被表示为多核组合形式. 由于多核(多类型核、多尺度核)决策函数具有更强的预测能力，能够逼近光谱回归函数中的不同成分， 本文中所提出的PLR算法在3个公共数据集上都展现出了比传统算法(如偏最小二乘回归和正则化最小二乘回归)更优的预测性能.

[1] Wold B S, Ruhe A, Wold H, et al. III, The collinearity problem in linear regression: The partial least squares approach to generalized inverses[J]. Siam Journal on Scientific & Statistical Computing, 2013, 5(3):735-743.

[2] Wold H.Soft modelling by latent variables: the nonlinear iterative partial least squares approach[M].Perspectives in Probability and Statistics, London:Academic Press:1975, 520-540.

[3] Haaland D M, Thomas E V, Chem A. Partial Least-Sqares Methods for Spectral Analyses.1. Relation to Other Quantitative Calibration Methods and the Extraction of Quantitative Information[J]. Analytical Chemistry, 1988, 60(11):1193-1202.

[4] Xu Y L, Chen D R, Li H X, et al. Least square regularized regression in sum space.[J]. IEEE Transactions on Neural Networks & Learning Systems, 2013, 24(4):635-646.

[5] Aronszajn A. Theory of reproducing kernels. Trans Am Math Soc[J]. Transactions of the American Mathematical Society, 1950, 68(3):337-404.

[6] Cucker F, Smale S. On the mathematical foundations of learning[J]. Bulletin of the American Mathematical Society, 2001, 39(1):332.

(责任编辑 赵燕)

Partially linear regression for multivariate calibration of spectroscopic data

GUO Lu, PENG Jiangtao, FU Huijing

(Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062, China)

Spectra-concentrate relation is usually a very complex and mixed linear relation.In this paper,a partially linear regression (PLR) algorithm is proposed for multivariate calibration of spectroscopic data.In PLR,the target regression function is represented as the sum of several linear and nonlinear kernel decision functions, where each single kernel function with specific type and scale can approximate certain component of the target function. The proposed method is compared, in terms of RMSEP, with partial least squares regression (PLS) and regularized least-squares regression (RLS) method on three real spectroscopic data sets.Experimental results demonstrate that the proposed PLR method shows superiority over PLS and the single kernel RLS.

partially linear regression; infrared spectroscopy; multivariate calibration

2017-06-01

湖北省教育厅中青年人才项目(Q20161003)资助

郭露(1992-)，女，硕士生；付辉敬，通信作者，讲师，E-mail: fxy0204@126.com

1000-2375(2017)05-0546-04

X36

A

10.3969/j.issn.1000-2375.2017.05.020