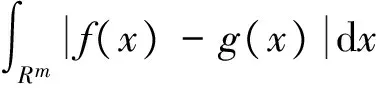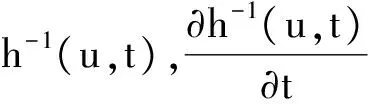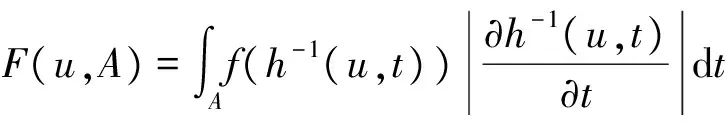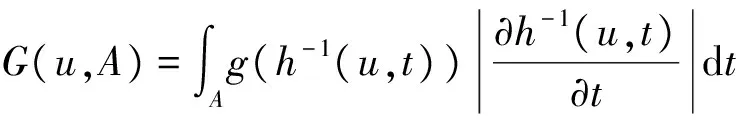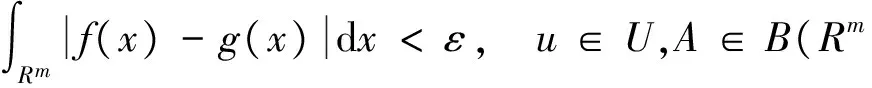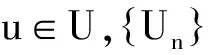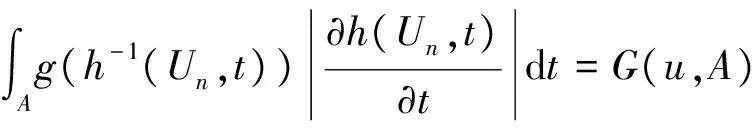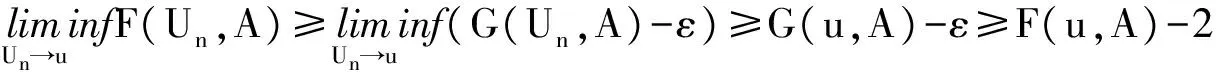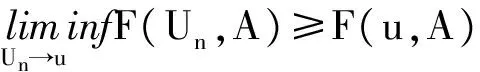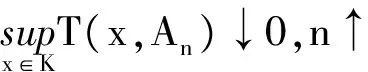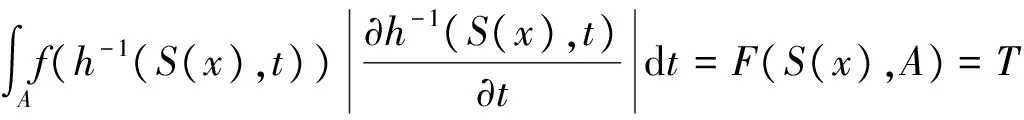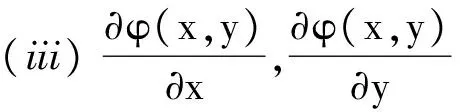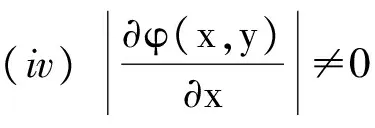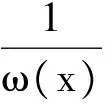非线性自回归序列一致可数可加性的一个充分条件

陈芬，张韧

(1.武汉学院信息及传播学院，湖北 武汉 430212; 2. 武汉华夏理工学院信息工程学院，湖北 武汉 430223)

非线性自回归序列一致可数可加性的一个充分条件

陈芬1，张韧2

(1.武汉学院信息及传播学院，湖北 武汉 430212; 2. 武汉华夏理工学院信息工程学院，湖北 武汉 430223)

讨论一类自回归序列满足一致可数可加性的一个充分条件.此时，自回归序列所对应的马氏链不具有不可约性.

非线性自回归；一致可数可加；马氏链

非线性时间序列，即使是很简单的非线性时间序列，它们显示出来的特点，也会令人们感到很新奇.由于非线性时间序列强大的应用性，目前它已被广泛地应用在经济、环境、生物和气候等领域[1].近年来，对非线性时间序列的研究取得了丰富的成果，见参考文献[2-3].众所周知，在对非线性时间序列模型进行统计性质研究时，模型的平稳性及其高阶矩的存在性是非常重要的指标，因此，众多学者专家对模型的平稳性及其高阶矩的存在性进行了广泛和深入的研究.

对非线性时间序列的研究方法，与线性时间序列有很大的差别.马氏链的理论方法是目前研究非线性时间序列的重要工具之一，大部分情况下，非线性时间序列都不是马氏链，但是通过扩大状态空间的方法，可以将其转化为马氏链.当非线性时间序列满足一定条件时，此时所对应的马氏链具有不可约性.而当非线性时间序列所对应的马氏链不具有不可约性时，一致可数可加条件是研究非线性时间序列的另一个有力的工具，见参看文献[4-6].

本文中利用马氏链的理论方法，找到判别一种应用广泛的非线性自回归序列满足一致可加性的一个充分条件，此时模型所对应的马氏链不具有不可性.

1 马氏链的基本知识及几个重要的模型

设Φ是定义在状态空间(X,B(X))上的一个马氏链，其中(X,B(X))是一个可分的可测空间，P(x,A)为Φ的一步转移概率核，Pn(x,A)为n步转移概率核，

为P的抽样链，其中a(k)为Z+上的概率测度.

定义1.1 称一步转移概率P满足一致可数可加条件，如果对任意的紧集K，有

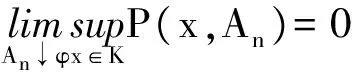
在非线性时间序列中，非线性自回归模型是线性自回归模型的自然推广，因其广泛的适用性而占有重要的位置.

考虑如下的p阶函数型随机方差非线性自回归模型，即存在Rp→R上的可测函数φ和Rp→[0,∞]上的可测函数ω，使得

Yn=φ(Yn-1,…,Yn-p)+εnω(Yn-1,…,Yn-p)

(1)

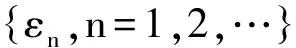
事实上，当p=1时，模型(1)是时齐马氏链，当p≥2时，模型(1)不是马氏链.此时令

则(1)式可记为

Xn=Φ(Xn-1)+εnω(Xnpn-1)e,n≥p

(2)

下面考虑更一般的自回归序列，存在Rm×Rm→Rm上的可测函数φ，使得

(3)

模型(3)是一个取值于状态空间(Rm,B(Rm))上的时齐马氏链，我们借助马氏链的理论，来研究模型(3)的平稳遍历性及其高阶矩的存在性，得到了模型(1.3)具有一致可数可加性的一个充分条件.

2 主要结果及证明

定理2.1 若模型(3)满足：

(i) 对∀i≥1，εi关于m维Lebesgue测度μ的绝对连续部分的密度函数f存在，且

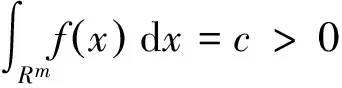
(ii) 函数φ满足：

(1) 存在开集U⊂Rn，函数h(z,y):U×Rm→Rm连续，

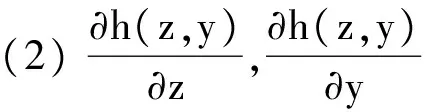
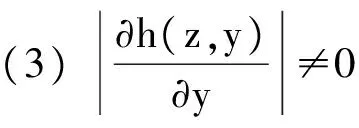
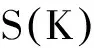
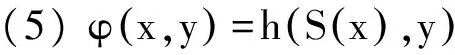
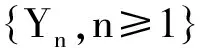
(a)Ka(x,A)≥T(x,A),x∈Rm,∀A∈B(Rm)，

(b)T(x,A)=c,x∈Rm，

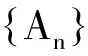
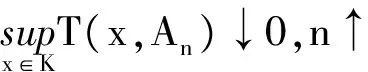
定理2.1的证明 由f∈L(Rm)可知，对∀0<ε

∀u∈U,A∈B(Rm)，令

则有

因此

(4)

由上式可知，对任意的A∈B(Rm)，有F(u,A)=F(u,Rm)-F(u,Ac)=c-F(u,Ac),

于是F(u,Ac)关于u是连续的.由Dini定理知对U中的任意紧集B，有

(5)

令

T(x,A)=F(S(x),A),x∈Rm,A∈B(Rm).

(6)

对Rm中的任意紧集K，由条件(4)中映射S的定义知，存在U中的紧集R，使得S(k)⊂R，结合(6)式，有

(7)

再由(5)式和(7)式有

此即结论(c)成立.

又由(4)式和(6)式知

T(x,Rm)=c, ∀x∈Rm.

此即结论(b)成立.

而Ka(x,A) ≥P(x,A)=P(x1∈A|x0=x)=P(φ(x,ε)∈A)=P(h(S(x),ε)∈A)≥

即结论(a)成立，从而定理2.1成立.

注： 定理2.1是一个应用广泛的定理，文献[5]中命题2.2.1可作为定理2.1的推论.

推论2.2 设模型(3)满足条件：

(i) {εn,n=1,2,…}有下半连续的密度函数f(t)存在，且f(t)>0，μm-a.s.,

(ii)φ(x,Rm)=Rm,∀x∈Rm,

则定理2.1结论成立.

推论2.2的证明 在定理2.1中取S(x)=x,U=Rm，则满足定理(2.1)中条件，从而结论成立.

最后，考虑模型(8)在p=1时的情形，即

Yn=φ(Yn-1)+εnω(Yn-1)

(8)

推论2.3 设模型(2.5)满足

那么定理2.1的结论成立.

推论2.3的证明 在定理2.1中令U=R×(0,∞)，h(z,y)=z1+z2y，Z=(z1,z2)∈U,y∈R，映射T:R→U，T(x)=(φ(x),ω(x))，记Φ(x,y)=h(T(x),y)，易验证Φ(x,y)满足定理2.1的条件，故推论2.3的结论成立.

[1] An H Z, Chen M. Nonlinear time series analysis[M]. Shanghai:Shanghai Science and Technology Press,1998.

[2] An H Z, Chen S G. A note on the ergodicity of nonlinear autoregressive models[J]. Statist Probab Lett, 1997,34:365-372.

[3] Brockwell P J, Povis R A. Time series analysis: theory and methods[M]. New York: Springer-verlag, 1998.

[4] Fonseca G,Tweedie R L. Stationary measure for mon-irreducible non-continuous markovchains with time series applications[J]. Statist Sini,2001,12(1):651-660.

[5] 盛昭瀚 .非线性时间序列模型的稳定性分析遍历性理论与应用[M]. 北京：科学出版社,1993.

[6] 张韧, 张绍义. 非线性自回归序列的平稳解及其矩阵的存在性[J]. 数学物理学报,2013(2): 260-266.

(责任编辑 赵燕)

A sufficient condtion for uniformly countable additiveof nonlinear autoregressive sequences

CHEN Fen1，ZHANG Ren2

(1. School of Information and Communication,Wuhan College, Wuhan 430212,China;2. School of Information Engineering, Wuhan Huaxia Institute of Technology, Wuhan 430223,China)

We study a sufficient condition of a class of autoregressive sequences for uniformly countable additive, and the corresponding Mokov chains don’t possess irreducibility.

nonlinear autoregressive; uniformly countable additive; Mokov chains

2017-06-01

湖北省自然科学基金(2016cfc747)资助

陈芬(1980-),女，硕士，讲师

1000-2375(2017)05-0539-03

O.211

A

10.3969/j.issn.1000-2375.2017.05.018