一类非带限信号的采样定理

周盼盼, 付应雄

(湖北大学数学与统计学学院, 湖北 武汉 430062)

一类非带限信号的采样定理

周盼盼, 付应雄

(湖北大学数学与统计学学院, 湖北 武汉 430062)

基于已有的一类多项式型阶梯滤波器, 构造一类有理函数型阶梯滤波器, 并给出对非带限信号的采样定理.

有理函数型阶梯滤波器; 广义Sinc函数; 采样定理

0 引言

对连续线性时不变系统而言, 其脉冲响应为h(t),当输入信号为fin(t) 时, 输出信号为fout(t), 且为h(t) 和fin(t)的卷积

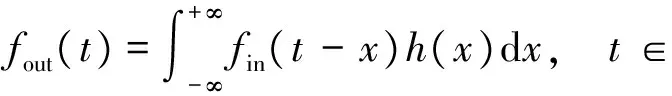
其在频域上等价表示为

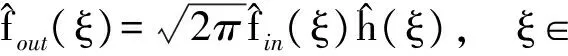
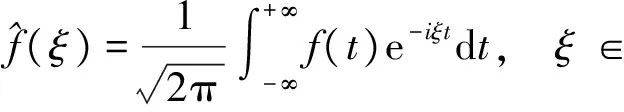
其脉冲响应为

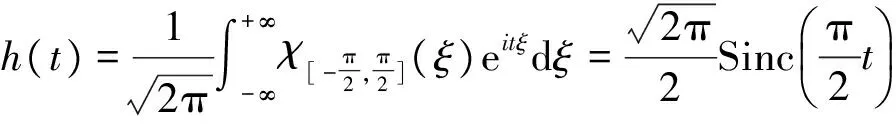
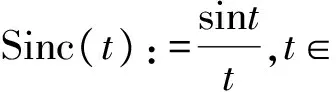
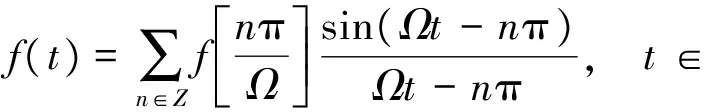
(1)

近年来, 众多文献关注非带限信号的采样定理, 其与广义 Sinc 有关, 其中广义 Sinc 函数

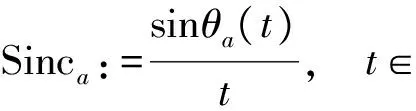
(2)

函数 eiθa(t) 是一个单位解析信号,其中

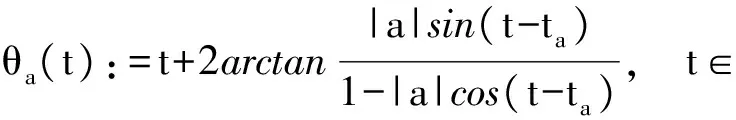
且满足

H(cosθa(t))=sinθa(t),

其中, Hf表示Hilbert变换

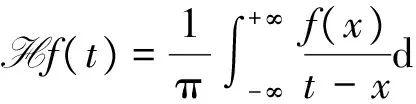
在文献[8]中利用一类多项式型阶梯滤波器给出非带限信号的采样定理. 对于 |a|<1, a∈,其滤波过程如下：

得到采样公式

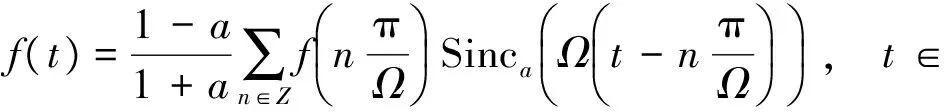
在文献[10]中提到了有理函数型阶梯滤波器,借鉴此思想, 本文中构造一类与文献[10]中不同的有理函数型阶梯滤波器并提出了对于非带限信号的采样定理. 为此,先将频率区间R 划分成对称区间：

In=[-(n+1)π,-nπ]∪[nπ,(n+1)π],n=0,1,2,….

对 |a|<1,a∈R,利用一类有理函数, 构造滤波器如下：

由此可得衰减的脉冲响应的频谱

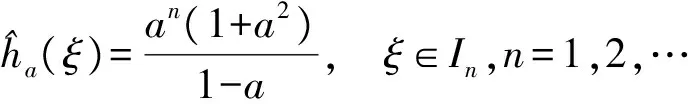
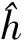
其在时间域上的表示为

(3)

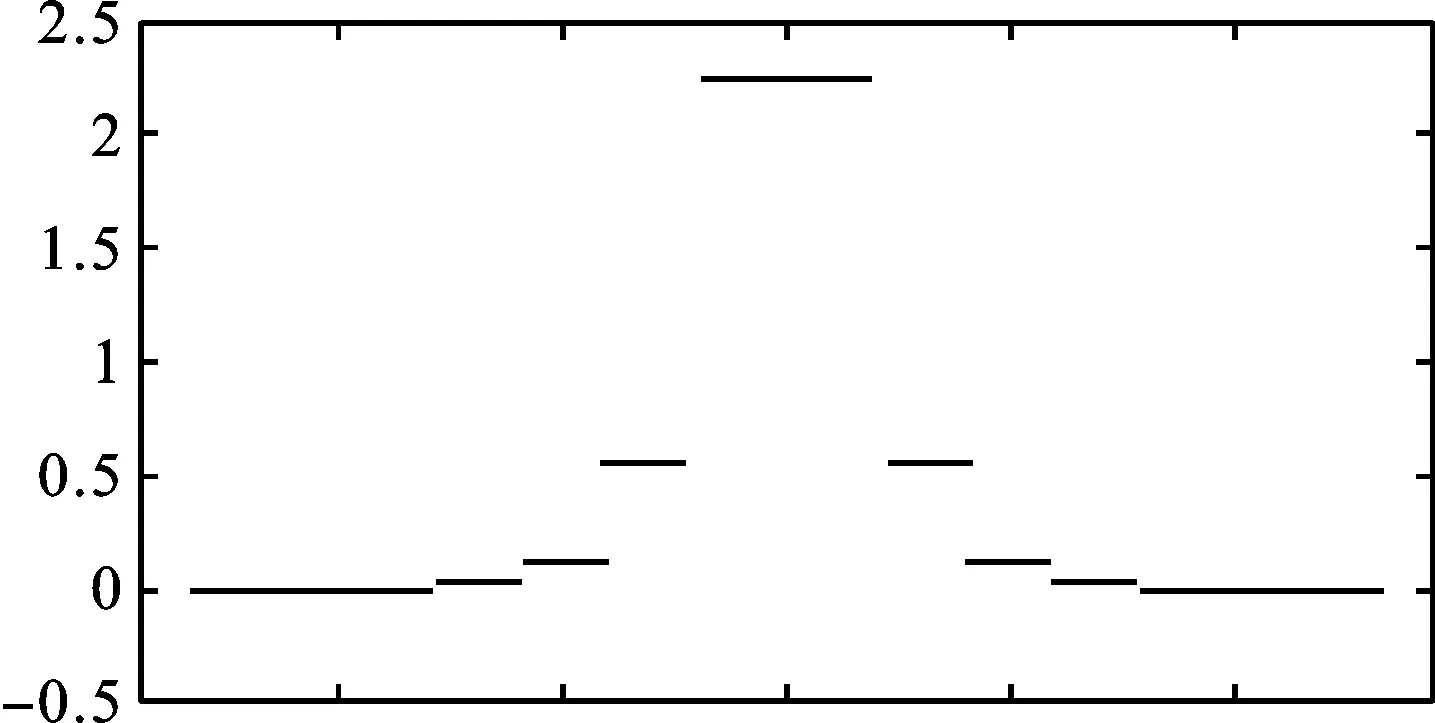
图1 有理函数形阶梯滤波

在文献[1-5]中指出

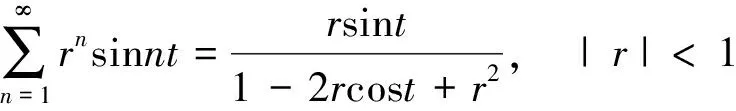
简单计算可得

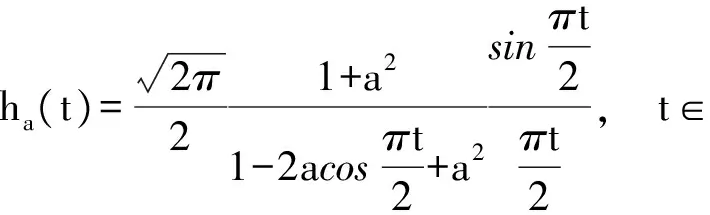
文献[5-7]中已经证明对于a∈, 得到

从而得到

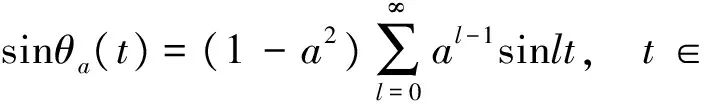
(4)

1 对非带限信号的采样定理

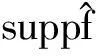
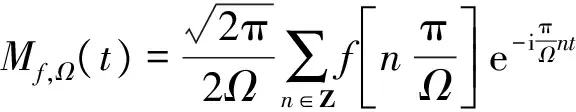
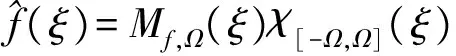
由此可定义空间

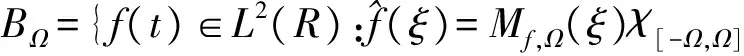
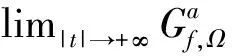
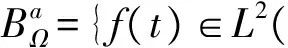
(5)

特别的，对于a=0,有

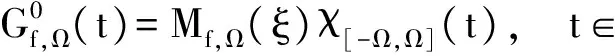
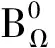
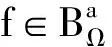
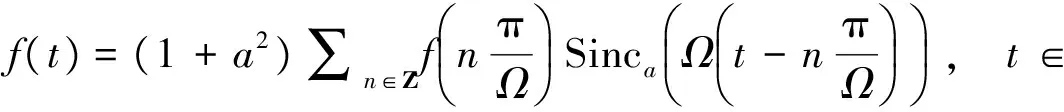
其中Sinca(·)为(2)式所定义.

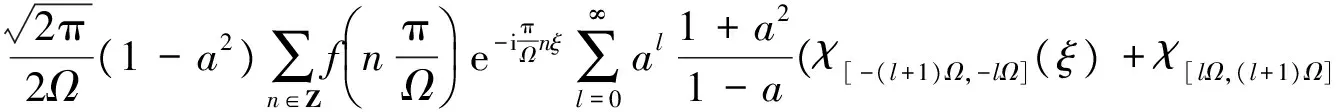
简单计算可得

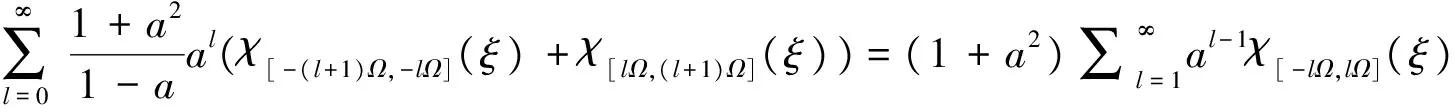
从而

(6)

由于

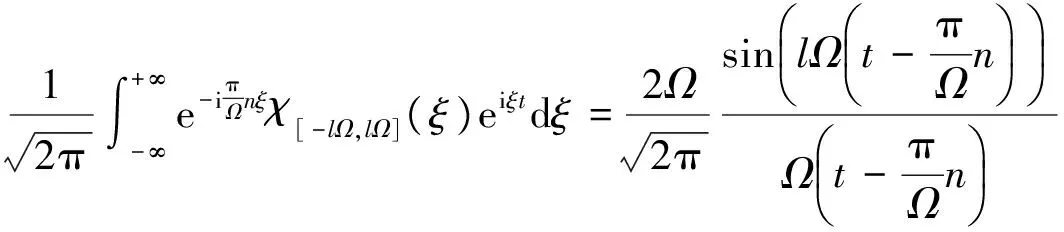
对(6)式两边应用傅立叶反变换得到

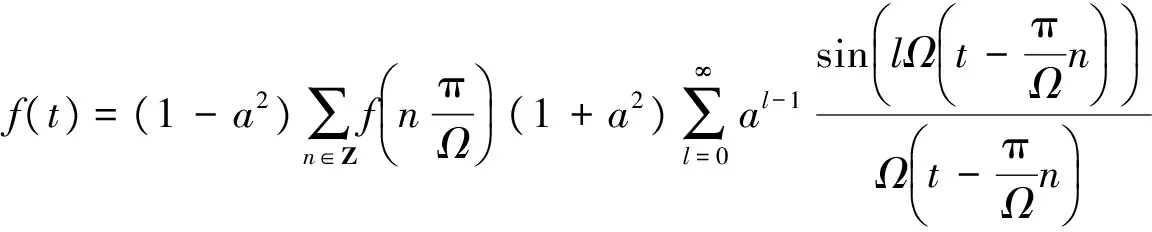
进而由 (4)式可得

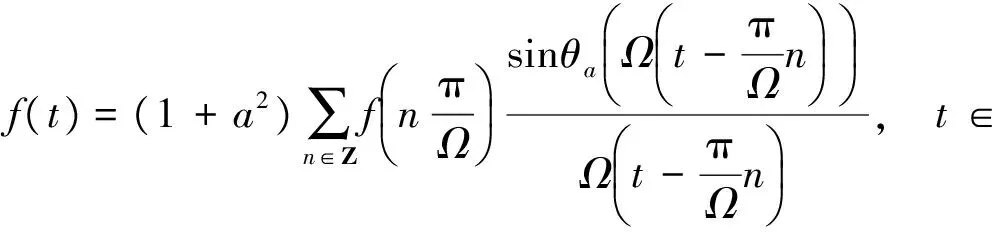
即

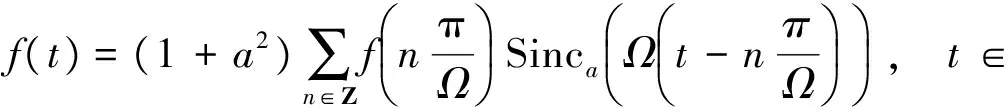
反之即得充分性, 证毕.

2 结论

经典采样定理仅对带限信号成立. 文献[8]中得到一类基于多项式型阶梯波谱的非带限信号采样定理. 笔者将多项式型阶梯波谱推广到一类有理函数型阶梯波谱, 其次将带限信号空间推广到非带限信号空间上, 进一步得到相应的非带限信号采样定理.

[1] Qian T, Chen Q H, Li L Q. Analytic unit quadrature singnals with nonlinear phase[J]. Physica D: Nonlinear Phenmena, 2005, 203(1): 80-87.

[2] Qian T. Unit analytic signals and harmonic measures[J]. Math Anal Appl, 2006, 314(1): 526-536.

[3] Chen Q H, Li L Q, Qian T. Time-frequency aspects of nonlinear fourier atoms[M]. In Wavelet Analysis and Applications, 2007, 2(1): 287-297.

[4] Chen Q H, Li L Q, Qian T. Two families of unit analytic signals with nonlinear phase[J]. Physica D, 2006, 221(1): 1-12.

[5] Qian T. Characterization of boundary values of functions in Hardy spaces with applications in signal analysis[J]. Journal of Integral Equations and Applications, 2005, 17(1): 159-198．

[6] Huang N E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proc R Soc Lond, 1998, 454(1): 903-995．

[7] Qian T, Huang N E, Riemenschneider S, et a1. A B-rspline approach for emperical mode decomposition[J]. Advances in Computational Mathematics, 2006, 24(1) : 171-195．

[8] Chen Q H, Qian T. Sampling theorem and multi-scale spectrum based on non-linear Fourier atoms[J]. Applicable Analysis, 2009, 88(6): 903-919.

[9] 赵春晖, 陈立伟, 马惠珠, 等. 数字信号处理[M].北京: 电子工业出版社, 2011.

[10] Liu Y L, Kou K I, Ho I T. New sampling formulae for non-bandlimited signals associated with linear canonical transform and nonlinear Fourier atoms[J]. Signal Processing, 2010, 90(3): 933-945.

(责任编辑 赵燕)

Sampling theorem for a class of non-bandlimited signals

ZHOU Panpan, FU Yingxiong

(Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062, China)

Based on the ladder-shape filter of polynomial, we construct a kind of ladder-shape filter of rational function and give a sampling theorem for non-bandlimited signal.

ladder-shape filter of rational function; generalized Sinc function; sampling theorem

2017-01-01

国家自然科学基金(11371007)资助

周盼盼(1991-), 女, 硕士生; 付应雄, 通信作者, 副教授

1000-2375(2017)05-0542-04

X36

A

10.3969/j.issn.1000-2375.2017.05.019