抓住根本，融会贯通

柯春红

摘要：数学习题课的教学要注重精选精练精评，教学教材的习题往往注重基础，但内涵丰富，可塑性强，要树立立足教材，深挖根本，融会贯通的习题教学观念，对典型习题积极展开研究，注重一题多解，一题多变，避免习题训练低水平的重复，是提高数学习题教学质量，培养学生发散思维，锻炼学生思维品质的重要途径。

关键词：习题；精选；变式；发散关于数学习题教学，著名数学家波利亚有一名名言：中学数学的首要任务就是加强习题训练，掌握数学就意味着解题。因此，习题课的教学历来被重视为数学课堂教学的一种重要课型。探究如何提高数学习题课的教学实效，显得更加有必要性与迫切性。纵使如此，我们的数学习题课还是存在诸多的弊端。第一，对于课堂习题课的教学往往会被认为是正课的一种补充与延伸而缺乏计划性。第二，习题课的备课往往没有正课的认真规范，缺乏目标与重难点。第三，习题课的课堂教学容易流入自由散漫的放羊式的教学，经常出现两个极端，要么是教师满堂灌，要么就是学生满堂练，题海战术。第四，也是最值得我们教师反思的一点，就是教师对于习题课题型的选择与加工缺乏研究，随意性很大。有人说，复习课与习题课最能显示教师的水平，我想，习题课的水平，最关键的就是教师的选题水平。有教师认为，现在网络这么发达，教学参考书多如牛毛，选题根本就不是问题，一搜索一下载复印就行了，其实问题就出现在这里，铺天盖地的题海耗费了学生教师的大量时间与精力，严重影响了教学的实效。数学习题的教学要注重基础性，系统性，可行性，针对性，更要通过习题的教学揭示知识的内在联系，使学生通过习题的练习与点评，完善知识的认知结构，掌握数学技能，归纳数学思想方法，发展数学思维，提高综合能力，达到这样的教学目标，精心挑选的典型的、有针对性的、有启发研究价值的习题，成为高质量习题课的硬件。减负，培优是教学的重任，选好题，就是最好的负责。

以下就八年级数学教材的选题、变式及其意图作几点例谈：

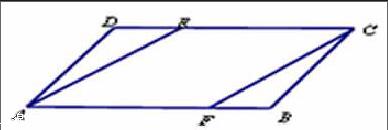
【选题例一】：已知：如图，在平行四边形ABCD中，BF=DE，求证：四边形AFCE是平行四边形。（原题出自教材P87习题2）

选题意图：

（1）平行四边形的性质与判定是本章的重要内容之一，此题题意简练，但综合了平行四边形的性质与判定的应用。

（2）本题可作以下变式，成为平行四边形性质与判定应用的巩固题型，且都是教材的题型。

变式①：图形不变，交换原题目条件与结论：已知：如图，在平行四边形ABCD中，AE∥CF，

求证：DE=BF。

变式②：

已知：如图，在平行四边形ABCD中，AC是对角线，E、F是对角线上的两点，且AF=CE，

求证：DF∥BE。

【选题例二】：已知，如图，在平行四边形ABCD中，∠ABC的平分线与AD相交于点P。

求证：（1）△ABP是等腰三角形。

（2）PD+CD=BC。（教材P88习题2）

变式①：已知，如图，在平行四边形ABCD中，∠ABC的平分线

与AD相交于点P，过点P作PQ∥AB。

求证：四边形ABQP是菱形。

变式②：已知，如图，在平行四边形ABCD中，∠ABC的平分线与AD相交于点P，过点P作PQ∥AB，连结PC，若PC平分∠BCD。

（1）求证：BP⊥PC；

（2）如果AD=8cm，AP=5cm，那么AB的长是多少？

△APB的面积是多少？

（原题型来自于教材P97知识技能1）

变式③：已知，如图，在平行四边形ABCD中，∠ABC的平分线与AD相交于点P，∠BDC的平分线与AD相交于点F

求证：AP=DF（原题型来自于教材P108习题12）

变式④：已知，如图，在平行四边形ABCD中，∠ABC的平分线与AD相交于点P，∠ADC的平分线与BC相交于点F。求证：DP=BF（原题型来自于教材P85习题3）。

变式⑤：已知：如图，平行四边形各角的平分线分别相交于点E，F，G，H。

求证：四边形EFGH是矩形。

选题意图：

（1）本题题意简练，但隐含平行四边形、等腰三角形、角平分线等重要性质。

（2）本题有广阔的拓展空间，且拓展题型也都来自于教材的习题。

（3）本题及其变式题的训练，充分体现了几何图形的生成、类比、转化、归纳的数学思想，对于发展学生的空间想象能力、逻辑推理能力、题型归纳能力，提高教学效率有重要的意义。

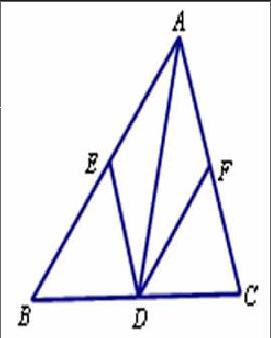
【选题例三】：已知：如图，AD是△ABC的角平分线，过点D分别作AC和AB的平行线，交AB于点E，交AC于点F。

求证：四边形AEDF是菱形。（教材P107习题6）

变式①：已知△ABC是等腰三角形，D，E，F分别是三角形三边的中点。

求证：（1）四边形AEDF是菱形。

（2）原条件上添加怎样的条件时，四边形AEDF是正方形。

变式②：已知D，E，F分别是三角形三边的中点，四边形AEDF是菱形。

求证：△ABC是等腰三角形（教材P104课堂练习题1）

选题意图：

（1）本题融合了特殊平行四边形、等腰三角形、角平分线、三角形中位线性质等重要性质。

（2）本题及其变式题的训练，充分体现了几何图形的生成、类比、转化、归纳的数学思想，对于发展学生的题型归纳能力，提高教学效率有重要的意义。

【选题例四】：

1.把以下△ABC通过适当的剪拼，组成一个平行四边形，请画出剪拼后的平行四边形，并说出你的发现。

2.把以下三角形，梯形，平行四边形通过适当的剪拼，組成一个矩形。并说出你的发现。

选题意图：

1.通过图形变换与操作，让学生领会三角形与四边形，四边形与特殊四边形之间的相互区别与内在联系，从而有效帮助学生构建合理的知识结构。

2.三角形的中位线是三角形中重要的相关线段，通过以上两题的类比训练，不仅可以让学生深刻领会三角形中位线性质与作用，还可以自然推广至梯形中位线的性质与作用（也是八年级上册教材中的一道习题）。

华南师范大学教授郭思乐教授一再强调数学教学一定要抓住文本的“根本”，文本的“根本”就在于深入挖掘教材，抓住知识生成的“根”，如此课堂教学就变得很简单。任何复杂的数学问题，我们都可以通过研究它的“根本”而追根溯源，教者能有这样一种指导思想来带领学生研究数学的话，正确有效的数学思维品质就植了“根”，数学学习一定会变得生机盎然，不再枯燥无味，这不正是我们要追寻的绿色课堂吗？（作者单位：佛山市南海区西樵镇樵北初级中学528200 ）endprint