关于B-Nekrasov矩阵线性互补问题最优误差界的注记
杨绍蓉,甘梦婷,李朝迁
(云南大学数学与统计学院,云南 昆明 650500)
关于B-Nekrasov矩阵线性互补问题最优误差界的注记
杨绍蓉,甘梦婷,李朝迁
(云南大学数学与统计学院,云南 昆明 650500)
研究了B-Nekrasov矩阵线性互补问题的含有参数误差界的最优值问题,利用函数的单调性,在的情况下,得到了该误差界的最优值.
B-Nekrasov矩阵;线性互补;误差界
1 引言
设
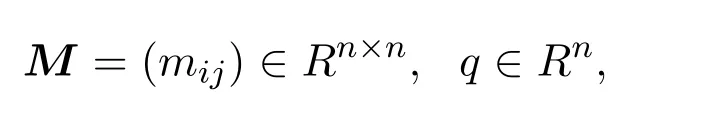
寻找解x∗∈Rn,使其满足:
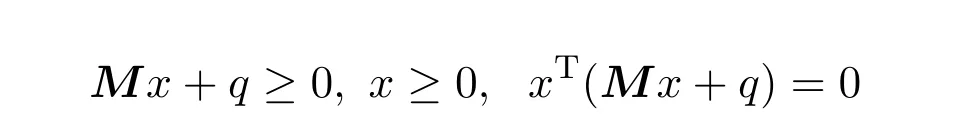
的问题称为线性互补问题,记为LCP(M,q)[14].其在经济学,对策论以及数学规划中起到重要的作用,是一类应用广泛的优化问题[5].LCP(M,q)解的存在性,唯一性,灵敏度以及求解算法的收敛性都与矩阵的结构和性质有关[6].当M 为P-矩阵时,LCP(M,q)存在唯一解[79].目前,该领域的热门研究课题之一是LCP(M,q)解的误差界估计,即给出的上界[7].
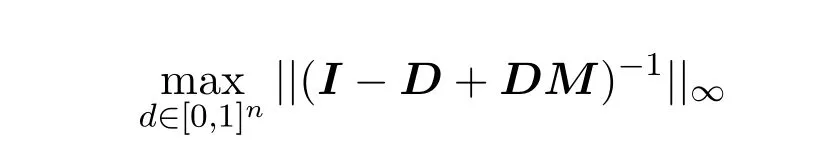
在文献[5]中提出了P-矩阵的子类矩阵B-Nekrasov矩阵,并给出其线性互补问题的误差界.对给定的矩阵
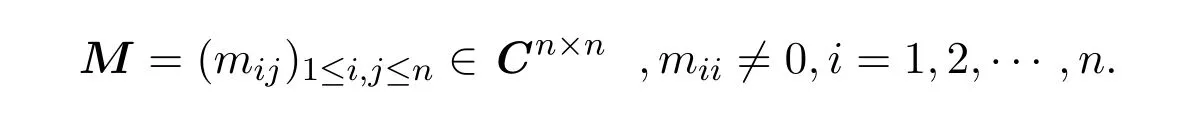

则称M为Nekrasov矩阵[8].
定义 1.1[10]设 A=(aij)1≤i,j≤n∈Rn×n,且 A 分解为 A=B++C 的形式,其中

若B+是对角元为正数的Nekrasov矩阵矩阵,则称A为B-Nekrasov矩阵.
定理 1.1[10]设 A=(aij)1≤i,j≤n,n≥2是 B-Nekrasov矩阵,并存在 m>i,使得
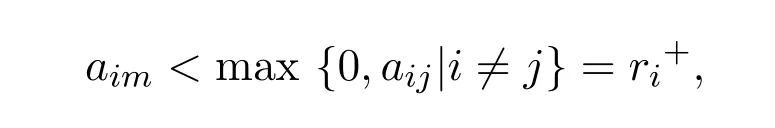
B+是定义1.1中所定义.对角矩阵
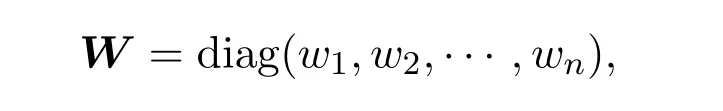
其中
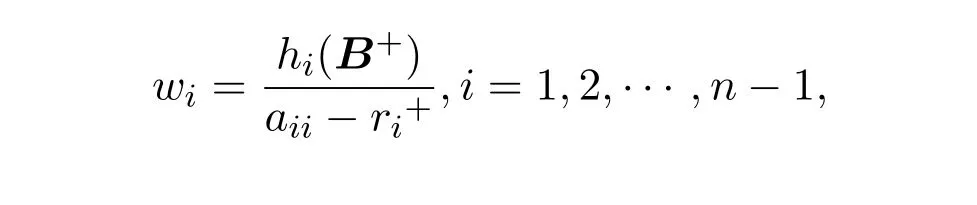

然而,在实际应用中往往取不同的ε计算f(ε)作为(1)式的近似值.
例1.1给定B-Nekrasov矩阵
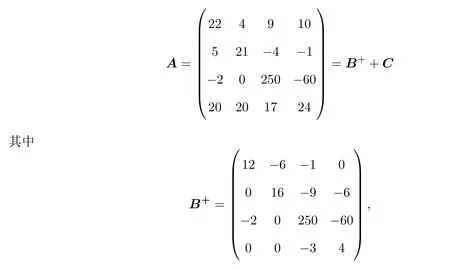
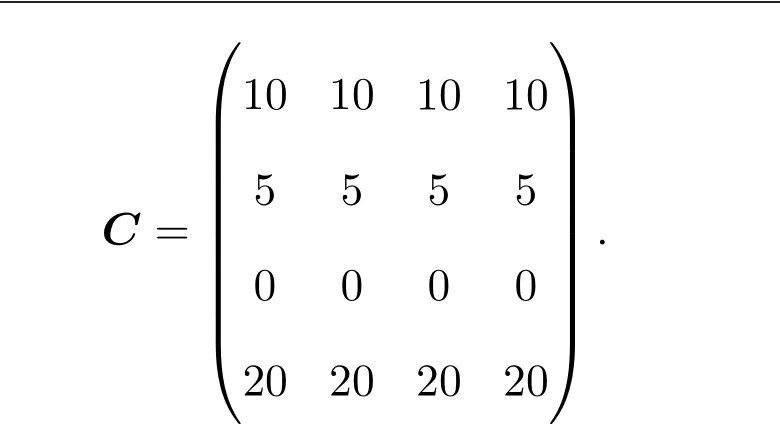
由定理1.1知,
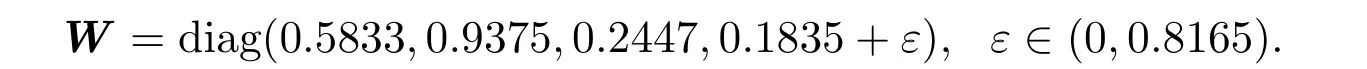
故可得定理1.1中的界f(ε),如图1所示.
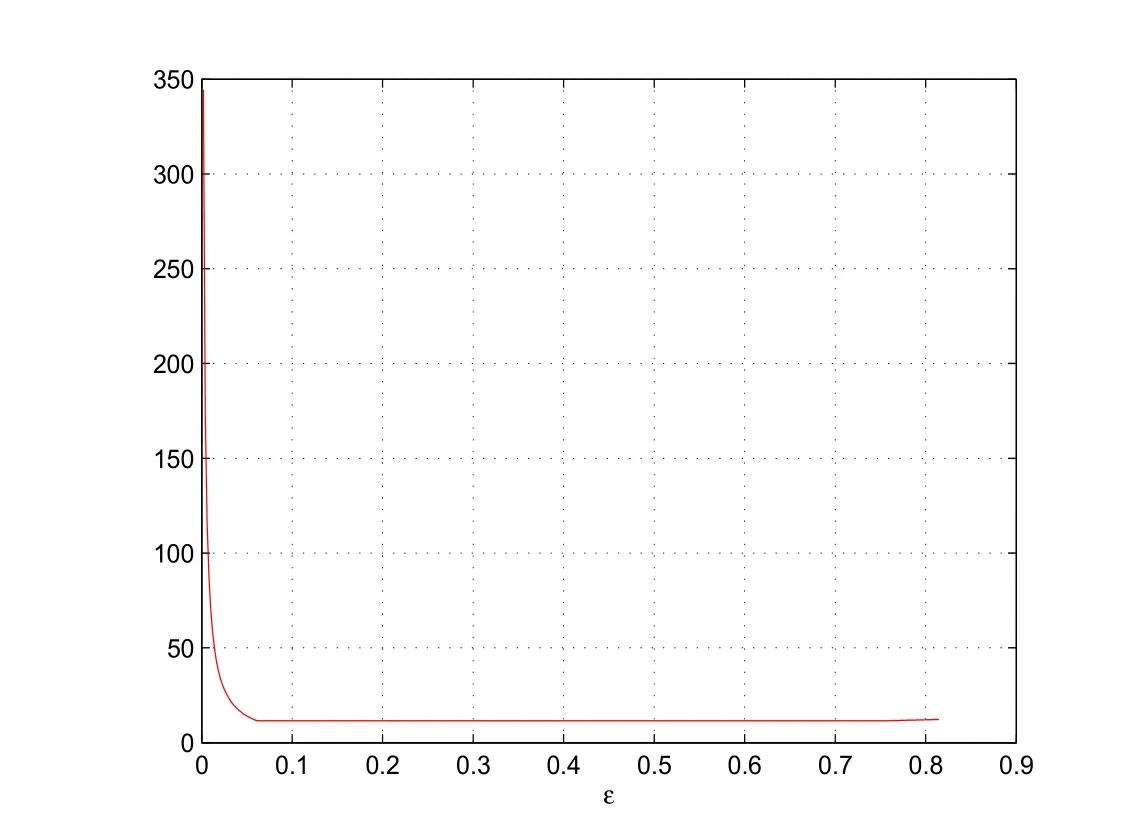
图1 例1的误差界
容易看出,当ε取值很小时(如ε=0.001,0.005),f(ε)的值很大,即ε的取值会导致界f(ε)非常大.另一方面,观察图1知
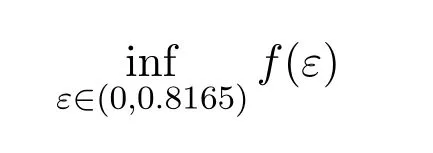
是存在的.然而,到目前为止,如何确定该值并没有相关结果?这将是本文的主要研究工作,即在给定的条件(δi>1,i=1,2,...,n-1)下,讨论了最优值问题,并确定(1)式的值.
2 B-Nekrasov矩阵的线性互补问题误差界的最优值
对满足定理1.1中的条件B-Nekrasov矩阵A,令
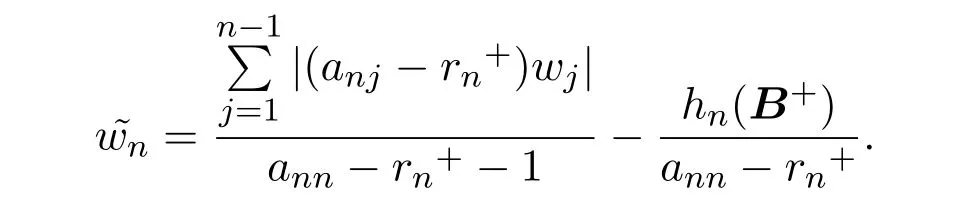
命题2.1设矩阵A,W,为定理1中所定义,且设 δi>1,i=1,2,...,n-1.
证明注意到
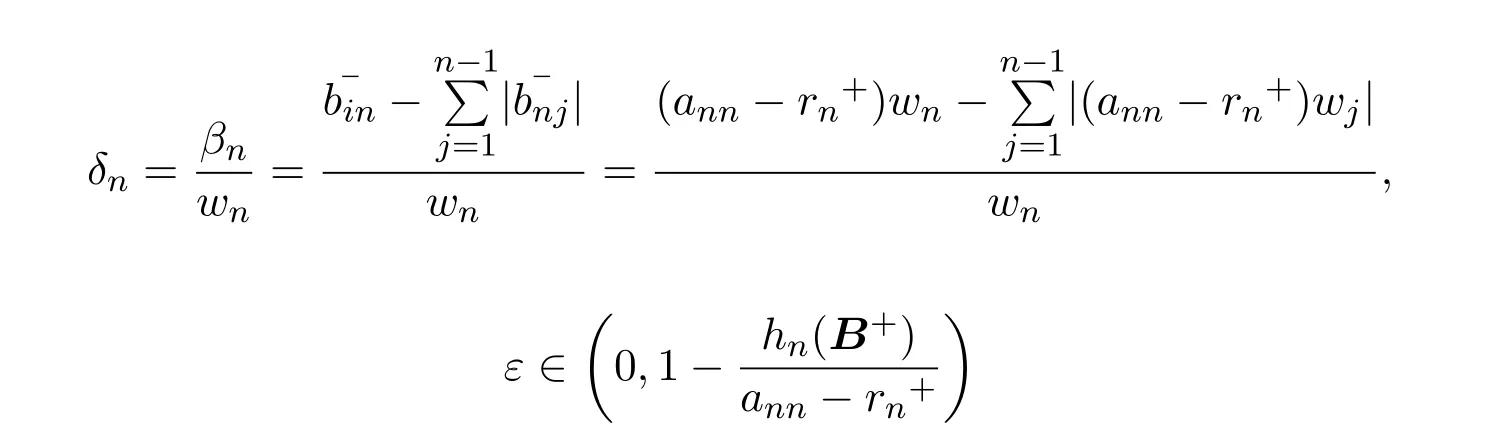
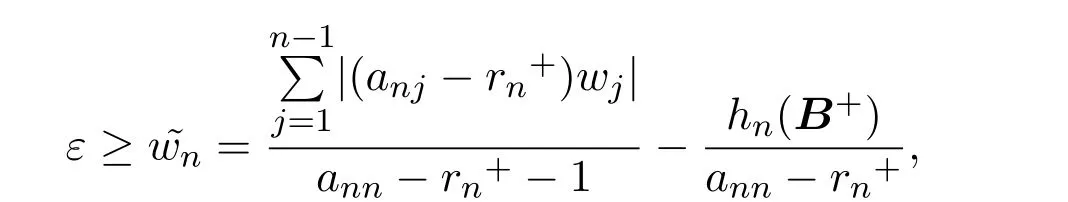
即
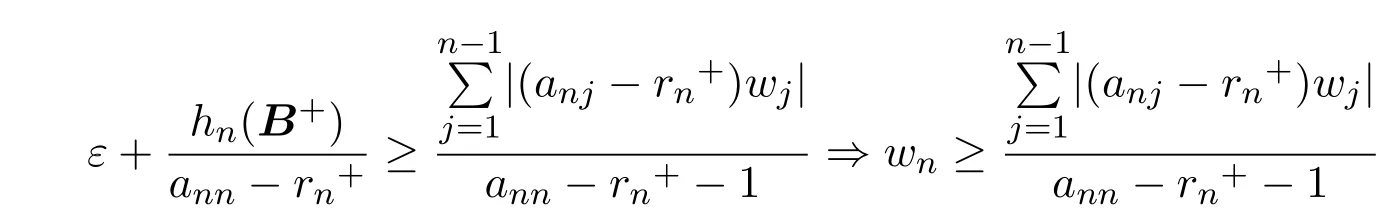
从而推出
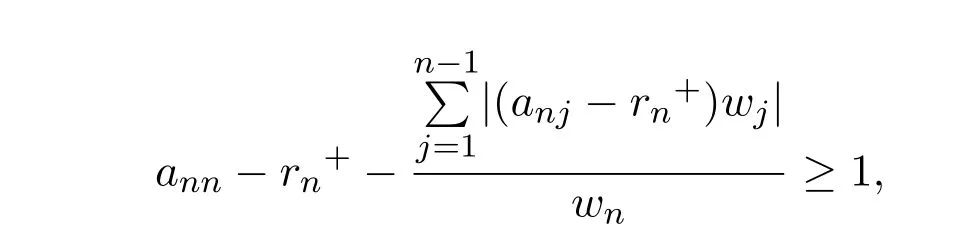
所以 δn≥1.故
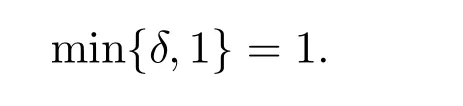
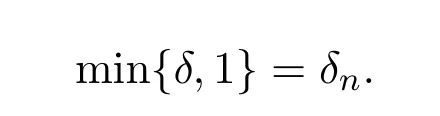
证毕.
进一步,对
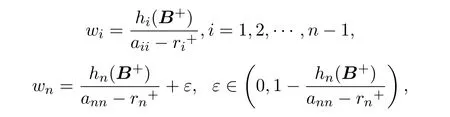
进行分析.不是一般性,设
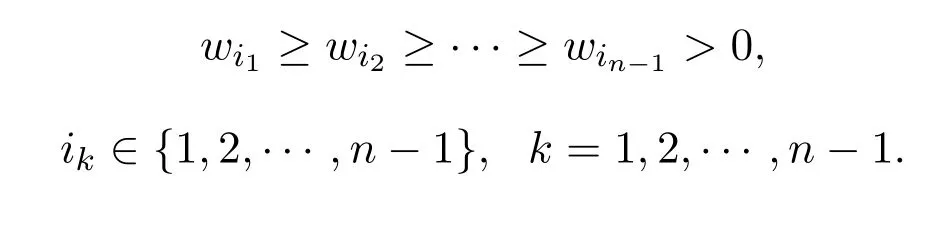


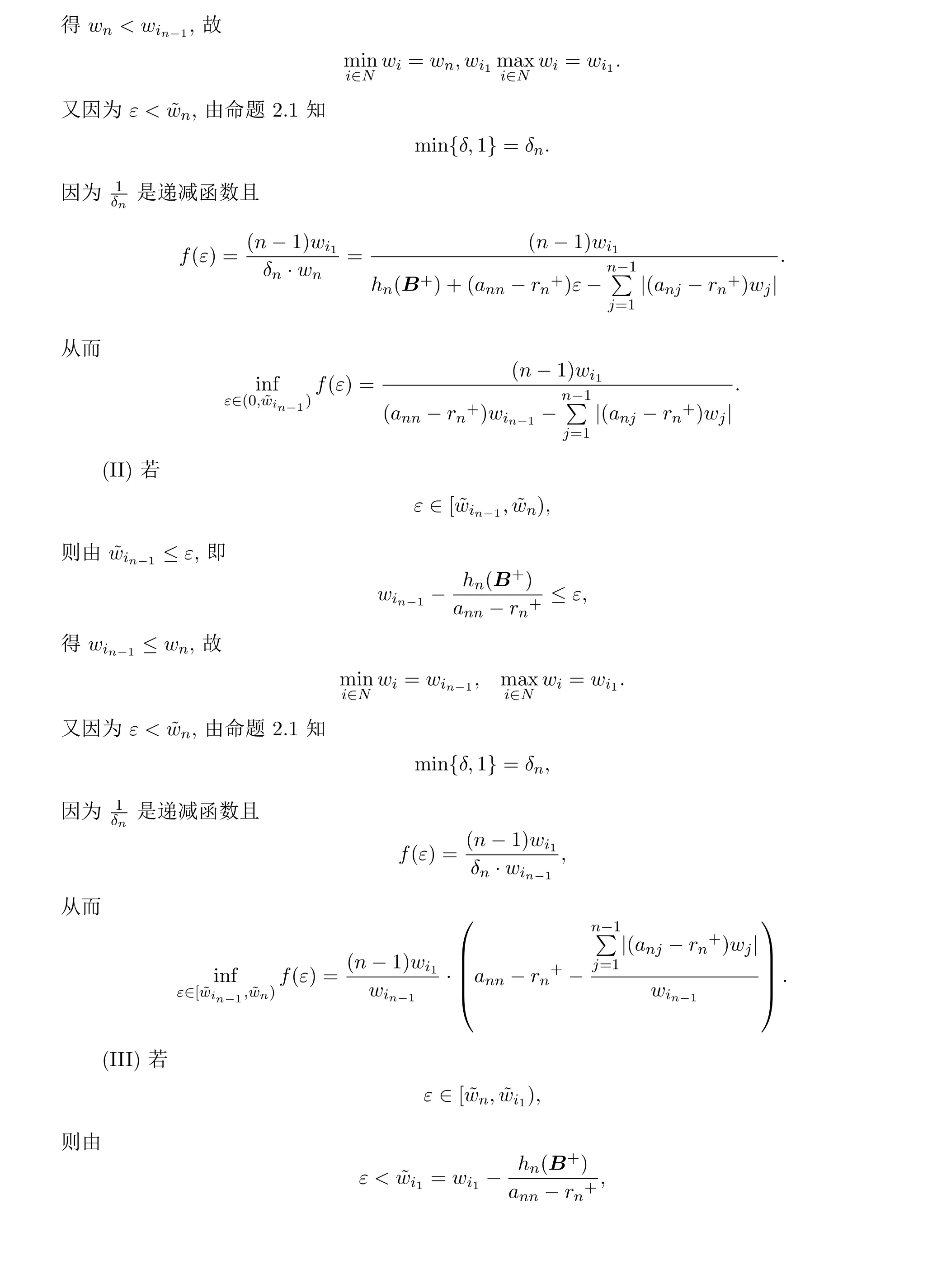


见图2.
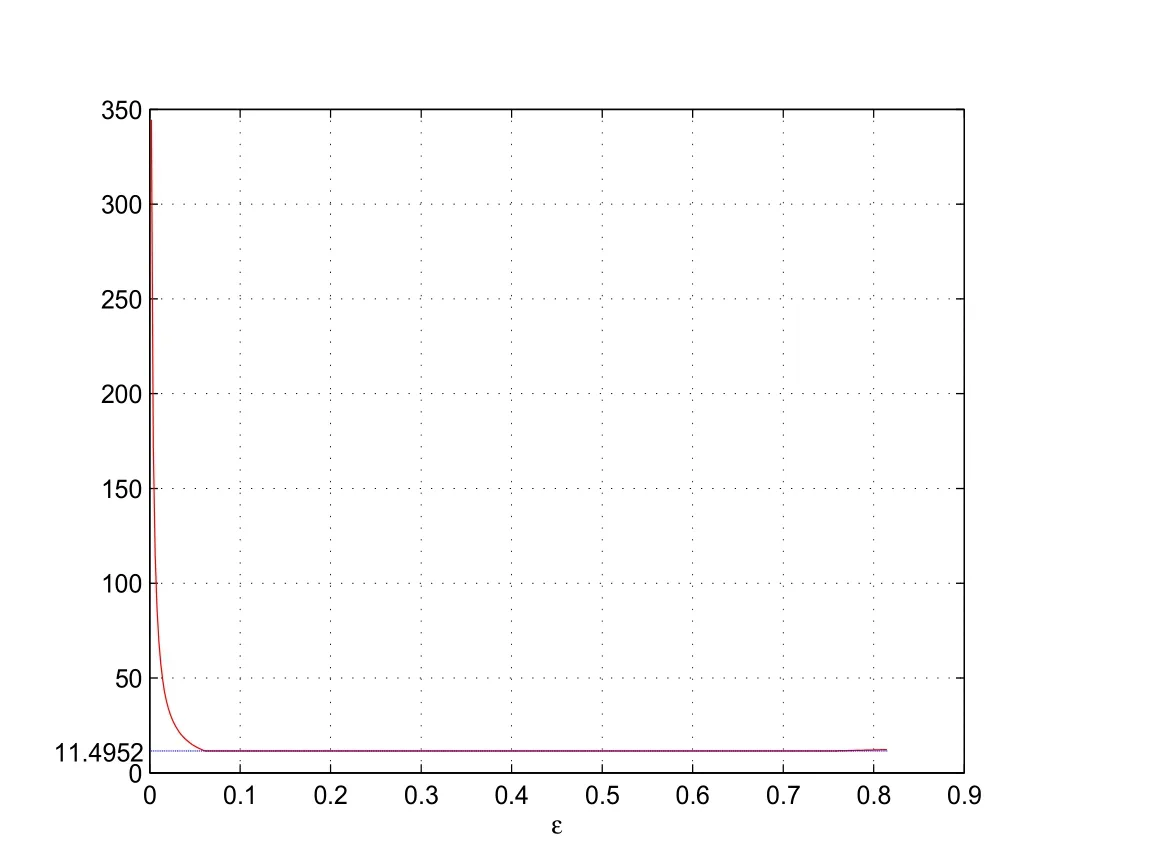
图2 误差界及其最优值
3 总结
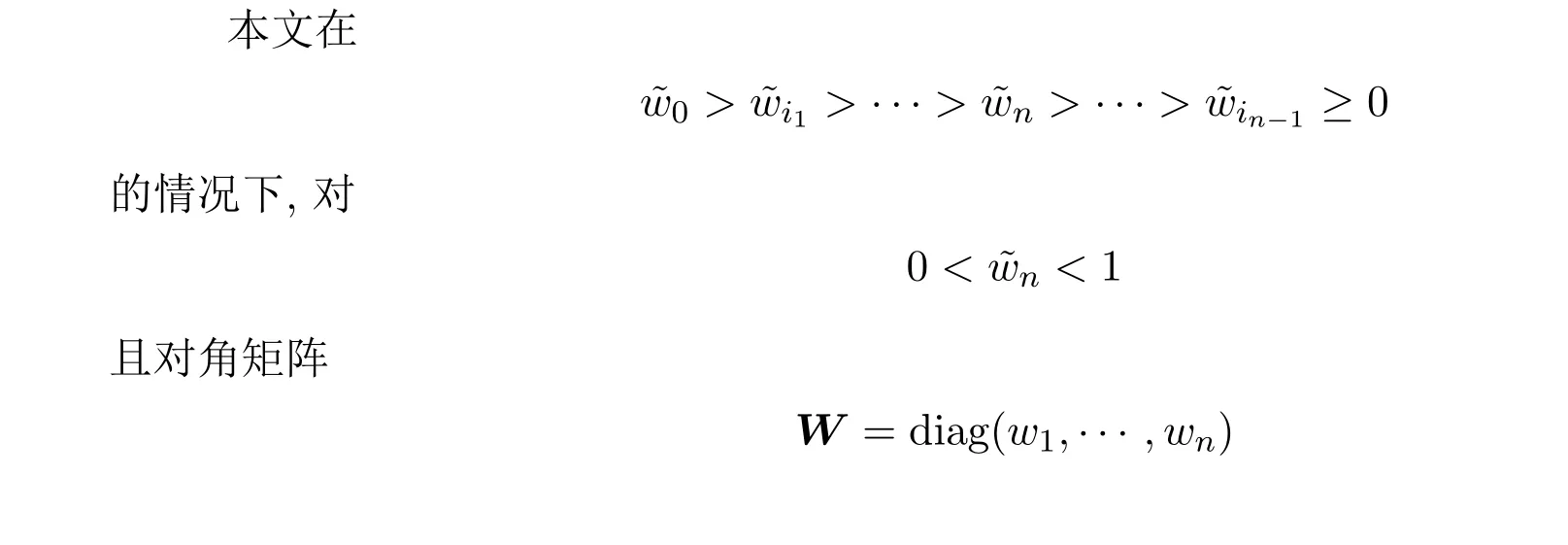
的元素均为正数进行讨论,讨论了f(ε)的最优值,这个最优值是存在且可计算的.对满足其它情况B-Nekrasov矩阵所对应的误差界f(ε)的最优值问题仍有待研究.
[2]Dai pingfan.Error bounds for linear complementarity problems of DB-matrices[J].Linear Algebra,2011,434:830-840.
[3]Li chaoqian,Gan mengting,Yang shaorong.A new error bound for linear complementarity problems for B-matrices[J].Electronic Journal of Linear Algebra,2016,31:476-484.
[4]Li chaoqian,Li yaotang.Note on error bounds for linear complementarity problems for B-matrices[J].Applied Mathematics Letters,2016,57:108-113.
[5]孙艳波.线性互补问题解的存在性及其相关矩阵的研究[D].南京:南京航空航天大学,2006.
[6]彭凌.几类特殊矩阵线性互补问题的误差界[D].吉首:吉首大学,2015.
[7]Chen xiaojun,Xiang shuhuang.Computation of error bounds for P-matrix linear complementarity problems[J].Math.Program,2006,106:513-525.
[9]Cottle R W,Pang J S,Stone R E.The Linear Complementarity Problem[M].New york:Academic Press,1992.
2010 MSC:60B12
《纯粹数学与应用数学》稿约
1本刊是经国家科委、新闻出版署批准公开发行的数学及其应用的综合性学术刊物,主要刊登数学学科中有创造性的研究论文和具有重要经济价值的应用性论文,以繁荣数学理论,推进应用数学研究.本刊2000年荣获《CAJ-CD规范》执行优秀奖,2004年入选全国中文核心期刊,2006年获陕西省出版编辑良好奖.2012年11月获陕西省科技期刊编辑学会2011-2012年度优秀科技期刊奖.
2本刊只接收中文稿件,2010起为双月刊,每年一卷,共6期,国内外公开发行.
3来稿要求和注意事项
3.1 来稿必须包括:题目、作者姓名、作者单位(全称)、作者简介(性别、年龄、职称、学位及主要研究方向)、中文摘要(200字左右)、关键词(3-5个)、中图分类号、2000年美国《数学评论》主题分类号、英文摘要、正文、参考文献.如有基金项目资助,请在文稿首页注明批准文号.
3.2 节段序号分别用1;1.1;1.1.1表示,稿件内容力求精炼充实,表述正确.摘要应说明论文的目的、方法、结果,结论和作用等.英文摘要必须与中文摘要一致,摘要中不出现公式与参考文献标识,尽量用语言叙述所得主要结果.摘要正文请用第三人称表述.
3.3 外文字母必须分清大小写、黑体(黑正体、黑斜体)、白体(白正体、白斜体)、花体;上下标的字母、数字和符号,其位置要区分明显,文中不要用同一个符号表示不同的意思.务请注明作者的联系电话和电子信箱.
3.4 文中插图请用描图纸黑墨绘制或由计算机打出,插图要清楚,线条均匀,要有图题;表格用三线表,要有表题;图、表要有中英文对照的图题和表题.
3.5 参考文献按文中引用的先后顺序编号,未公开发表的资料请勿引用.文献书写格式如下:
(1)书籍:作者(姓在前).书名[M].版次(初版不写).出版地:出版社,出版年.
(2)书籍中的析出文献:作者(姓在前).论文题名[M]//专著责任者.专著题名.出版地:出版社,出版年:起止页码.
(3)译著:原作者 (姓在前).书名 [M].版次 (初版不写).译者姓名.出版地:出版社,出版年:起止页码.
(4)期刊论文:作者(姓在前).论文题名[J].期刊名,年,卷(期):起止页码.
(5)论文集中的析出文献:作者(姓在前).论文题名 [C]//论文集责任者.论文集名.出版地:出版社,出版年.
(6)学位论文:作者(姓在前).学位论文题目[D].收藏地:收藏单位,答辩年份.
(7)电子文献:作者 (姓在前).题名 [EB/OL].出版地:出版社,出版年 [引用日期].获取或访问路径.
4来稿经审查后,编辑部有权对来稿作适当文字修改.来稿不退,请作者自留底稿.稿件刊登后,赠送该期刊2册.作者如需改投它刊,可通知本刊编辑部.
5本刊不刊登已发表过的文章,请勿一稿多投.
6本刊采用网上投稿,敬请关注本刊网站(http://puremathe.paperonce.org/).
A note on the optimal error bounds for linear complementarity problems of B-Nekrasov matrices
Yang Shaorong,Gan Mengting,Li Chaoqian
(College of Mathematics and statistics,Yunnan University,Kunming 650500,China)
The optimal error bound with a parameter of linear complementarity problems of B-Nekrasov matrix is studied.By using the monotonicity,in the case of,the optimal value of the error bound is obtained.
B-Nekrasov matrix,linear complementarity,error bounds
O241
A
1008-5513(2017)04-0430-11
10.3969/j.issn.1008-5513.2017.04.010
2017-04-26.
国家自然科学基金(11601473).
杨绍蓉(1993-),硕士,研究方向:数值代数.
李朝迁(1986-),博士,副教授,研究方向:数值代数.

