一个模恒等式的新证明

朱军明， 胡廷锋

(洛阳师范学院数学科学学院， 河南洛阳 471934)

一个模恒等式的新证明

朱军明， 胡廷锋

(洛阳师范学院数学科学学院， 河南洛阳 471934)

本文利用Jacobitheta函数构造椭圆函数，并利用椭圆函数的性质证明了模恒等式

Jacobitheta函数；椭圆函数；模恒等式；留数

1 引言及说明

等式

(1)

本文目的在于给出等式(1)的一个新证明. 为此, 假定q=eπiτ且lmτ>0.

为了方便, 定义

(a,b,…,c;q)∞=(a;q)∞(b;q)∞…(c;q)∞.

直接验证易得

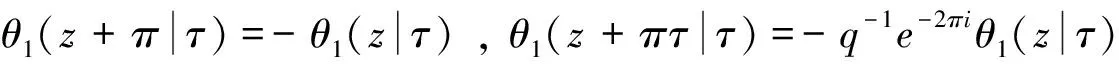
2 等式(1)的证明

我们的证明基于椭圆函数的如下性质(见文献[3]第15页 ).

引理 设P是椭圆函数f(x) 的基本平行四边形,f(x) 在P的边界∂P上没有奇点,那么f(x) 在P内的留数之和等于零.

证明 令

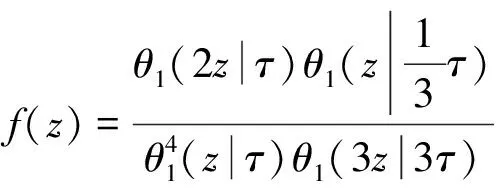
f(z+π)=f(z) ,f(z+πτ)=f(z) .

从而f(x) 是以π和πτ为周期的椭圆函数.

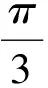
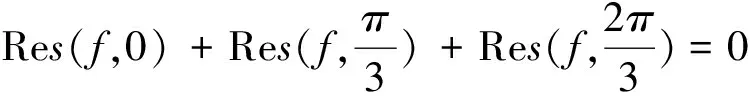
(2)

以下只要分别计算f(x)在这三点的留数即可.

为了计算Res(f,0),令F(z)=z3f(z),则

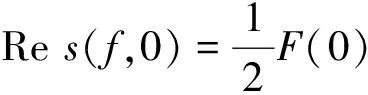
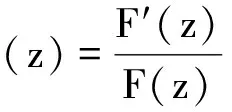
通过求对数导数可得

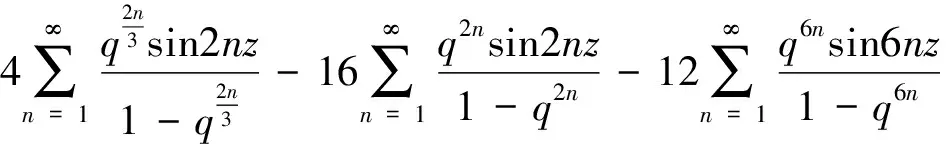
于是

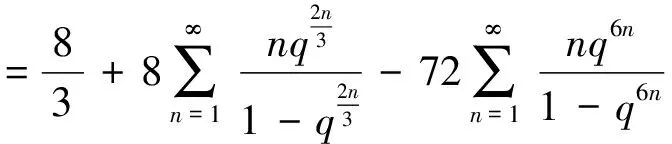
又

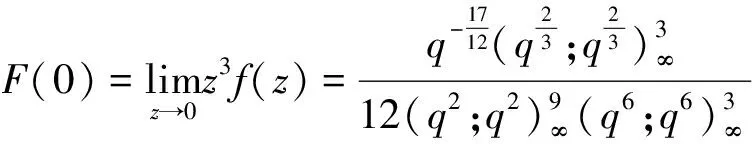
从而

把三点的留数值代入(2),整理得到

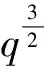
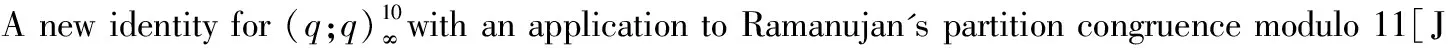
[2] Borwein J M, Garvan F G. Approximations toπvia the Dedekind eta function, in Canadian Mathematical Society Conference Proceedings[J]. American Mathematical Society, Providence, RI, 1997, 20：89-114.

[3] 阿西泽尔 Н И. 椭圆函数论纲要[M]. 刘书琴, 纪琁， 译. 北京： 商务印书馆, 1956.

[责任编辑 胡廷锋]

A New Proof of a Modular Identity

ZHU Jun-ming, HU Ting-feng

(College of Mathematics and Science, Luoyang Normal University, Luoyang 471934, China)

Jacobithetafunction;ellipticfunction;modularidentity;residue

2017-05-05

国家自然科学基金项目(11371184)

朱军明(1973—)， 男， 湖水应城人， 博士， 副教授. 研究方向：q一级数和theta函数.

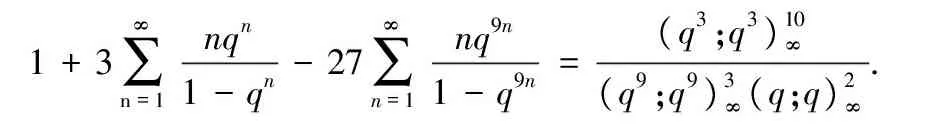
O156

A

1009-4970(2017)08-0001-02