系泊系统的优化设计

谭 兵， 黄辉红， 陈桂糖

(西南石油大学理学院， 四川成都 610500)

系泊系统的优化设计

谭 兵， 黄辉红， 陈桂糖

(西南石油大学理学院， 四川成都 610500)

系泊系统是近浅海观测网的重要组成部分，如何设计最优的系泊系统从而促进信号的传播具有重要的意义．本文围绕着系泊系统的设计问题展开讨论，通过三力汇交平衡理论和力矩平衡方程确定系泊系统中各个参数之间的联系，利用悬链线方程解得锚链的受力、形状，解决了在确定锚链的型号、长度和重物球的质量的情况下，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小的问题，给出了最优系泊系统设计的方案．

系泊系统；三力汇交平衡；悬链线方程；多目标规划

0 引言

近浅海观测网的传输节点由浮标系统、 系泊系统和水生通讯系统组成. 系泊系统具有成本低、 结构简单、 方向性好等显著优点， 因此在海洋工程中获得了广泛的应用[1]. 目前系泊系统在海上油田开发、 船舶防风以及援救打捞作业场布置中都有十分广泛的应用. 本文基于2016年全国大学生数学建模竞赛A题， 对系泊系统的设计问题进行了分析研究.

系泊系统的设计问题就是确定锚链的型号、 长度和重物球的质量， 使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小，本文需解决如下三个问题.

问题1 某型传输节点选用Ⅱ型电焊锚链22.05m， 选用的重物球的质量为1200kg. 现将该型传输节点布放在水深18 m、 海床平坦、 海水密度为1.025×103kg/m3的海域. 若海水静止， 分别计算海面风速为12 m/s和24m/s时钢桶和各节钢管的倾斜角度、 锚链形状、 浮标的吃水深度和游动区域.

问题2 在问题1的假设下， 计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域. 调节重物球的重量，使得钢桶的倾斜角度不超过5度，锚链在锚点与海床的夹角不超过16度.

问题3 由于潮汐等因素的影响， 布放海域的实测水深介于16～20m之间. 布放点的海水速度最大可达到1.5m/s、 风速最大可达到36 m/s. 给出考虑风力、 水流力和水深情况下的系泊系统设计，分析不同情况下钢桶、 钢管的倾斜角度、 锚链形状、 浮标的吃水深度和游动区域.

说明 近海风荷载可通过近似公式F=0.625×Sv2(N)计算， 其中S为物体在风向法平面的投影面积(m2)，v为风速(m/s). 近海水流力可通过近似公式F=374×Sv2(N)计算， 其中S为物体在水流速度法平面的投影面积(m2)，v为水流速度(m/s).

1 模型的假设与符号说明

1.1 模型假设

1.假设系泊系统中各个连接部件不存在摩擦力的损耗.

2.假设没有人为的外力来影响系泊系统.

3.假设不考虑海水的侵蚀等对钢管锚链等质量的影响.

4.假设海水中没有其他生物来影响系泊系统.

1.2 符号的说明

符号说明见表1.

表1 符号说明

2 模型的建立与求解

2.1 问题1的模型建立与求解

首先采用整体隔离法， 对浮标、 钢管、 钢桶、 锚链和所参考的整体进行受力分析， 通过三力汇交平衡理论和力矩平衡方程建立各变量之间的函数关系. 再引入悬链线模型并根据需求对其进行合理改进， 得到锚链满足的函数关系. 对水深的约束和系泊系统各部分在法向方向上的高度， 建立目标函数并进行求解.

2.1.1 受力分析与关系式的建立

系统的受力分析见图1.

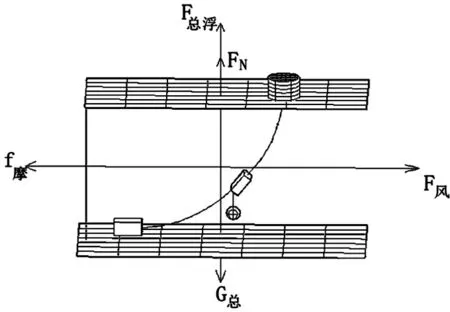
图1 整个系统的受力分析

通过三力汇交平衡理论可以得到水平方向与竖直方向的关系式：

然后分别对各个单个的物体进行受力分析.

针对浮标的受力分析(图2).

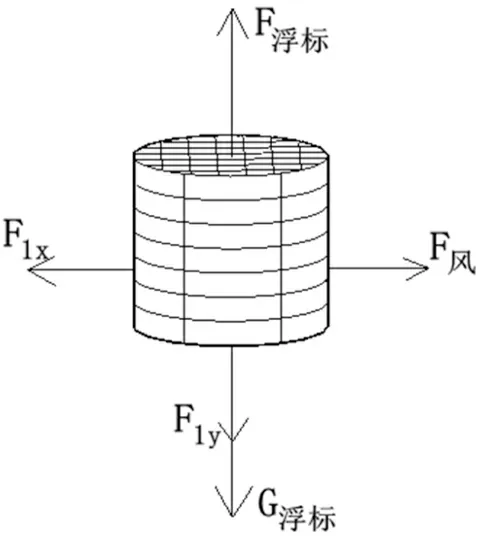
图2 浮标的受力分析

其中F1x，F1y分别为钢管1对于浮标的拉力在水平方向以及竖直方向上的分解. 同时为了求解各个钢管以及钢桶的倾角， 需要考虑力矩平衡. 针对后面钢管的分析同理. 可以分别得到水平方向与竖直方向上的关系式：

针对钢管1的受力分析(图3).

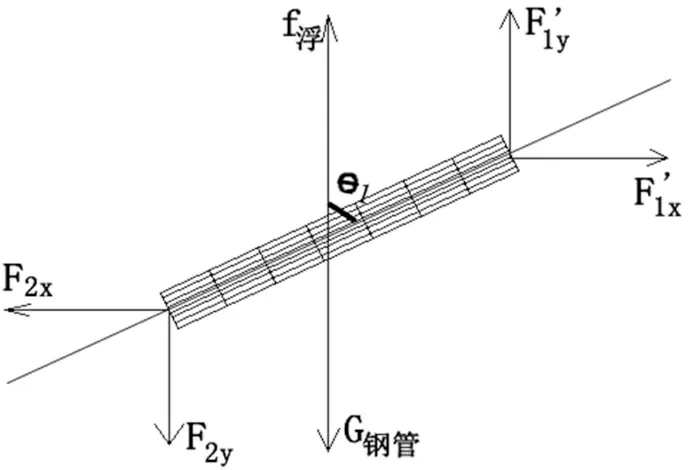
图3 钢管1的受力分析

其中θ1即为钢管1的倾斜角度. 水平方向以及竖直方向上的关系式满足

其力矩平衡的方程为

F1ysinθ1+f浮sinθ1×0.5=G钢管sinθ1×0.5+F1xcosθ1

对其余钢管受力分析方法类似， 我们可得到各钢管的力矩平衡方程

Fiysinθi+f浮sinθi×0.5=G钢管sinθi×0.5+

Fixcosθi(i=1， 2,3,4)

针对钢桶进行受力分析(图4).

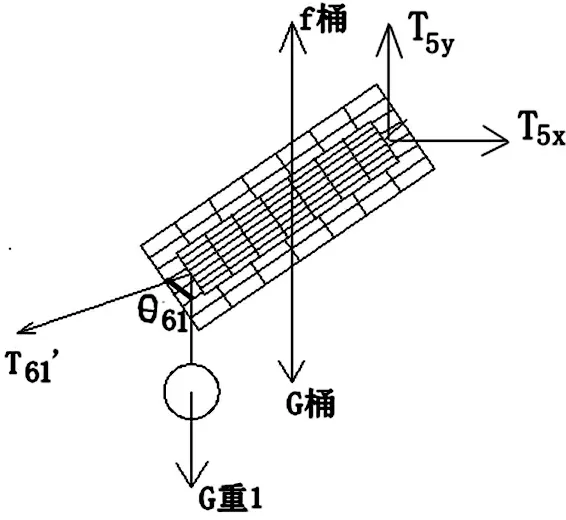
图4 对钢桶进行受力分析

根据图4可以分别得到水平方向与竖直方向上的关系式

以重物链接的点作为支点的力矩平衡方程为

F5ysinθ5+f桶sinθ5×0.5=G桶sinθ5×0.5+F5xcosθ5

2.1.2 锚链的相关模型建立

通过查找资料可以了解到锚链的相关计算[2]， 即悬链线方程的计算， 需要用到微分的思想.

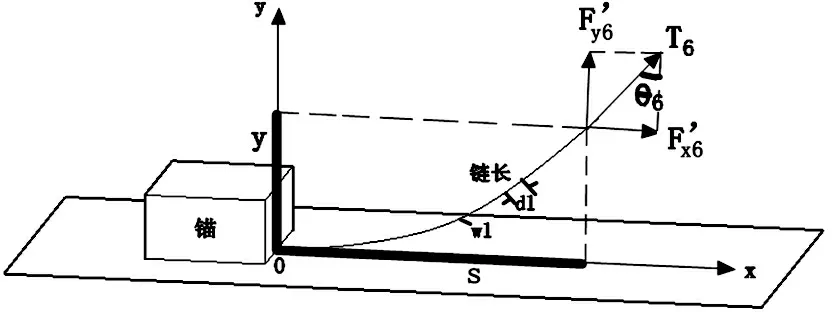
图5 悬链线示意图

图5为锚链上任意一缆索元的静力[3],其中w是缆索的单位长度重量,dl为悬链线长度，T6为张力,dT为张力在dl上的增量,θ为的方向锚链下端切线方向与水平线的夹角,dθ为θ在dl上的增量. 通过在锚链AB段上的积分， 沿水平与垂直方向建立平衡方程

通过微分可得到悬链线方程

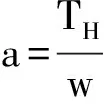
由于所有的未知量均可以用吃水高度h表示， 通过题目中所给出的约束条件水深H=18， 建立目标函数， 当z最小时可得到h近似最优解.

minz=H-h+(cosθ1+cosθ2+cosθ3+cosθ4+cosθ5)×1-y0

2.1.3 模型的求解

吃水深度， 各个钢管的倾角， 钢桶的倾角以及悬链长度， 悬链在x上的投影长度， 浮动区域半径随风速变化的参数如表2所示.

表2 不同风速下解得的不同参数

通过数据可知， 在风速为12m/s的情况下， 存在卧底锚链的长度l'1=6.8169m. 风速为24m/s的情况下， 存在卧底锚链的长度l'2=0.3133m.

然后通过上述悬链方程可以作出锚链形状(图6).

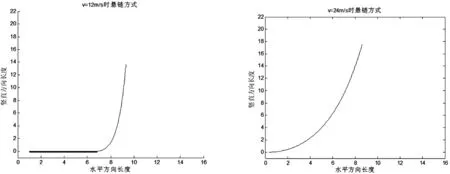
图6 不同风速下的锚链形状

2.2 问题2的模型建立与求解

在问题1的模型基础上， 将风速为36m/s代入问题1中的模型求解， 通过MATLAB编程仿真， 绘制得到风速为36m/s时锚链的形状， 具体数据如表3所示.

表3 在风速为36m/s的情况下各个参数的数值

通过分析上表数据得到在风速等于36m/s的情况下， 钢桶的倾角θ5大于5度， 则需要重新调整重物的重量.

锚链形状如图7所示.

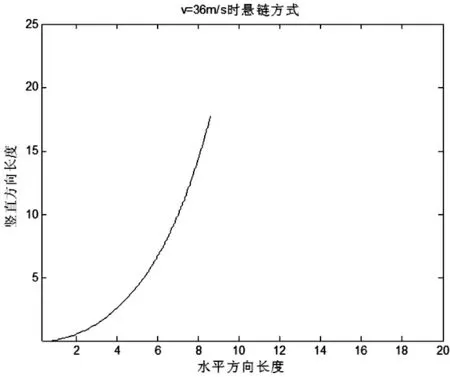
图7 风速为36m/s情况下的锚链形状

问题2研究的是基于题目给出的：钢桶的倾斜角度不超过5度的情况， 锚链在锚点与海床的夹角不超过16度的情况. 因为存在两个目标函数， 所以为了简化问题， 可以考虑逐步逼近. 首先使钢桶的倾斜角等于5度， 通过问题1中的模型解出吃水深度和重物的质量， 并由该解出值计算锚链在锚点与海床的夹角， 若求得锚链在锚点与海床的夹角大于16度， 则不满足情况， 应舍去， 需要增大重物的质量继续取值， 直到所得角满足条件. 具体求解的流程图如图8所示.

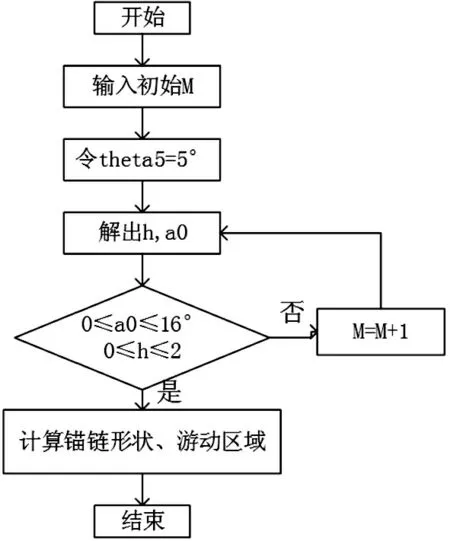
图8 首先考虑钢桶的倾斜角的流程图

考虑与此类似的情况， 假设锚链在锚点与海床的夹角等于16度， 同理可以解出一个吃水深度和一个重物的质量， 并由该值计算钢桶的倾角. 若大于5度则不满足情况， 则需要增大重物的质量继续取值.

通过问题1的受力分析可以得到锚链在锚点与海床的夹角的一个关系表达式：

化简得tan∂与吃水深度h和重物球的质量m相关的表达式， 即

对钢桶进行隔离受力分析得到钢桶的倾角

又因为

通过对问题1进行受力分析可以得到

F风=F1x=F2x=F3x=F4x=F5x

整理上述公式可以得到钢桶的倾角用吃水深度h表达的计算公式， 即

此时我们可建立重物质量m只与锚链在锚点与海床的夹角和钢桶的倾角相关的表达式， 同时考虑约束条件即

求解目标函数：

minm=φ(∂,θ5).

应用MATLAB编程[4]， 通过换算， 得到m关于∂和θ5的关系， 并逐步代入∂(0-16°)， θ5(0-5°)解得m的值：

minm=2289.7kg.

所以需要调整的重物球质量最小为2289.7kg.

2.3 问题3的模型的建立与求解

针对问题3题目中所给出条件， 由于增加了水流力的情况需要对研究系统重新进行受力分析. 并且当风力与水流力的方向相同时， 可以求得极端情况. 所以在本文中认为风力与水流力的方向相同， 并且通过问题1对风力夹角的分析， 可以假设水流力与海平面的夹角也为零度.

本文考虑海域深度为16～20米、 海水速度最大为1.5m/s及风速最大为36m/s时， 建立使浮标的吃水深度、 游动区域以及钢桶的倾斜角度达最小的多目标规划模型. 由于风速和海速自变量即考虑锚链的型号， 长度和中重物球质量. 由于在题目中说明， 由于考虑极端情况， 所以风速， 海水速度记取最大值. 同时假定风力与海流力为同一方向. 锚链型号依次带入方程式计算， 海水深度由20m开始取值， 依次取20,19,18,17,16计算.

得到多目标规划模型,目标函数如下

约束条件：

通过无量纲[5]转化系数将多目标规划模型转化为单目标函数求解

minf(h,θ5,D) =

然后利用MATLAB优化工具箱[6]进行优化求解. 选取重物的变化范围在2200～5000kg， 步长取100kg. 解出在不同深度的情况下各个倾角如表4所示.

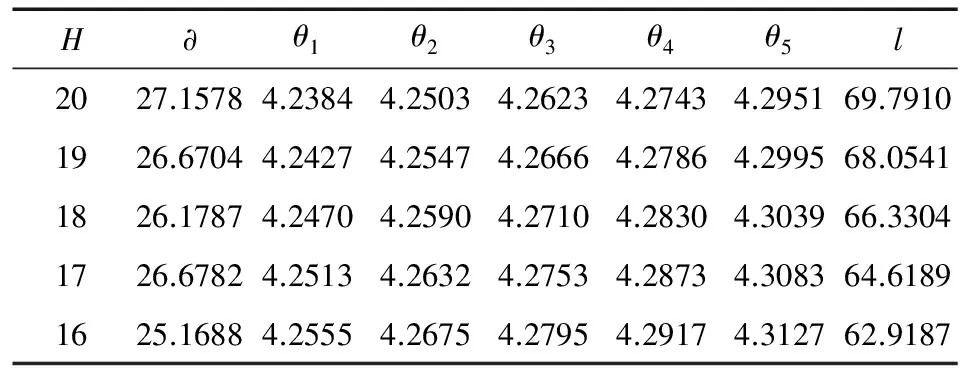
表4 不同深度下各个钢管以及钢桶的倾角

[1] 徐建鹏.系泊系统的三维动力学分析及实验研究[D].中国海洋大学, 2014.

[2] 王文明, 张世联. 流花浮式平台锚链系统安全评估[J]. 造船技术,2007(4).

[3] 何静. FPSO悬式锚腿系泊系统的锚系设计研究[D]. 武汉: 武汉理工大学, 2007.

[4] 赵海滨. MATLAB应用大全[J]， 北京：清华大学出版社， 2012.

[5] 米尔斯切特, 刘来福,等. 数学建模方法与分析[M]. 北京： 机械工业出版社, 2015.

[6] 赵静,但琦.数学建模与数学实验[J].北京:高等教育出版社， 2008.

[责任编辑 胡廷锋]

Optimum Design of Mooring System

TAN Bing, HUANG Hui-hong, CHEN Gui-tang

(College of Science, Southwest Petroleum University, Chengdu 610500, China)

Mooring system is an important part of near shallow sea observation network, which promotes the spread of signals. As a consequence, designing an optimal mooring system is of great significance. In this paper, our objective is to build a mathematical model to develop a best design for the system. Firstly, we analyze the relationship among the parameters in the mooring system by the three-force convergence theory and the moment balance equation, and get the force and shape of the anchor chain by the catenary’s equations. Then we determine the type and the length of the anchor chain, as well as weight of the heavy ball. Based on the above conditions, we calculate the draft depth of the buoy, the swimming area of the buoy and the tilt angles of steel drums. In addition, we also consider that the values of the parameters are changed due to different wind speeds and sea speeds. Hence, we use the multi-objective optimization scheme to constrain the angle and ultimately obtain an optimal design of the mooring system.

mooring system; three force transfer balance; catenary line equation; multi-objective programming

2017-03-05

谭兵(1995—)， 男， 四川广安人, 西南石油大学理学院2014级本科生. 研究方向：应用数学.

U653．2

A

1009-4970(2017)08-0009-05