旋转矢量在光的干涉和衍射中的应用
陈学文 姚 雪 张家伟 陈震亚
(重庆科技学院数理学院,重庆 401331)
旋转矢量在光的干涉和衍射中的应用
陈学文 姚 雪 张家伟 陈震亚
(重庆科技学院数理学院,重庆 401331)
旋转矢量在讨论两个及两个以上简谐振动合成的问题时,是一种很方便的工具。利用旋转矢量分析计算光的干涉和衍射光强分布十分简洁直观,而无需涉及复杂的积分计算,且得到的结果与利用菲涅尔衍射积分公式得到的结果一致。利用旋转矢量讨论光的干涉和衍射问题可加深同学对振动合成、干涉和衍射相关知识的整体理解。本文利用旋转矢量具体讨论了光的干涉和单缝衍射的条纹分布和光强分布。
旋转矢量;光的干涉;光的衍射;光强分布
光的干涉和光的衍射是工科大学物理课程中十分重要的组成部分。然而,由于光的干涉和光的衍射涉及到知识点多且抽象,以及工科大学物理学时的限制,目前大多数大学物理课程中关于单缝夫琅禾费衍射条纹分布,一般采用菲涅尔半波带法定性讨论,对衍射光强的分布,一般只给出光强分布公式I=I0sin2β/β2;而在讨论光栅衍射时,对于多缝干涉的讨论,也仅仅讨论主明条纹产生条件(光栅方程),并以结论的形式说明两条相邻的主明条纹之间有N-1条暗条纹和N-2条次级明条纹。所以在实际教学中,学生普遍感到内容分散且抽象,公式多且容易混淆,于是很难区分光的干涉和衍射现象产生明暗条纹的条件和条纹分布特点。因此,若能采用一种较为简洁的方法分析计算多缝干涉和单缝衍射条纹和光强分布,对于工科大学生较为深入理解光的多缝干涉、单缝衍射和光栅衍射(多缝干涉和单缝衍射总效应)大有帮助。针对如何在大学物理课堂上讲好光的干涉和衍射相关知识,学术界从不同方面对此做了研究与探讨。文献[1]探讨了启发式教学在物理光学课堂教学中的应用;文献[2]也探讨了如何改善波动光学教学方法;文献[3]结合马文蔚主编的《物理学》(5版)教材探讨了大学物理中光学教学的探究与思考。文献[4-7]分别从不同方面探讨了光的干涉与光的衍射之间的区别于联系。
“旋转矢量”是一种描述简谐振动较为直观的几何方法。从坐标原点O(平衡位置)画一矢量,使它的模等于谐振动的振幅A,并令t=0时A与x轴的夹角等于谐振动的初相位φ0,然后使A以等于角频率ω的角速度在平面上绕O点作逆时针转动,这样作出的矢量称为旋转矢量。旋转矢量任一时刻在x轴上的投影x=Acos(ωt+φ0)就描述了一个简谐振动。它在讨论波(光)的干涉和衍射时十分方便。利用旋转矢量讨论光的干涉和衍射光强条纹分布时十分方便而无需涉及复杂的积分计算,并且得到的结果与利用菲涅尔衍射积分公式得到的结果一致。基于此,本文利用旋转矢量法具体讨论光的多缝干涉和夫琅禾费单缝衍射的条纹分布和光强分布,以期以一种较为简洁直观的方法使学生掌握光的干涉衍射相关知识,并加深同学对振动合成、干涉和衍射相关知识的整体理解。
1 利用旋转矢量讨论光的多缝干涉
对于由N个狭缝构成的多缝干涉,其装置简图如图1所示。狭缝中的光传播到P点时,相邻两条狭缝传播到光屏上P点的光程差为Δ=dsinθ,则相邻两束光在P点振动的相位差
(1)

图1 多缝干涉示意图
相应的旋转矢量合成(叠加)如图2所示。根据几何关系可得,每一个分振动的振幅为Ai=2r(sinΔφ/2),N个旋转矢量的合振幅为A=2rsin(NΔφ/2)。

图2 多缝干涉旋转矢量叠加
P点合振动的振幅
(2)
其中,A0=NAi。光的强度与振幅的平方成正比,定义光的强度I=A2。则P点光强为
(3)
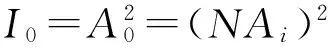
对于N=2的特例(此时为杨氏双缝干涉),根据式(2)可得
(4)


次级明条纹对应的条件式为
(5)
在Δφ≠2kπ的条件下(根据上文讨论Δφ=2kπ对应着主极大值条件),可得,
(6)


图3 N个旋转矢量干涉相长相消的示意图
图4根据多缝干涉光强分布公式(3)给出了3缝、6缝、10缝和20缝干涉光强分布。可以看出,相邻两主明条纹之间有N-1条暗条纹,有N-2条次级明条纹,且次级明条纹比主明条纹强度小很多,随着缝数的增加,次级明条纹的强度逐渐减小。对于N很大的多缝干涉,在屏上看到的条纹是很细很亮的条纹中间有宽阔的暗区域。

图4 多缝干涉光强分布(a) N=3; (b) N=6; (c) N=10; (d) N=20
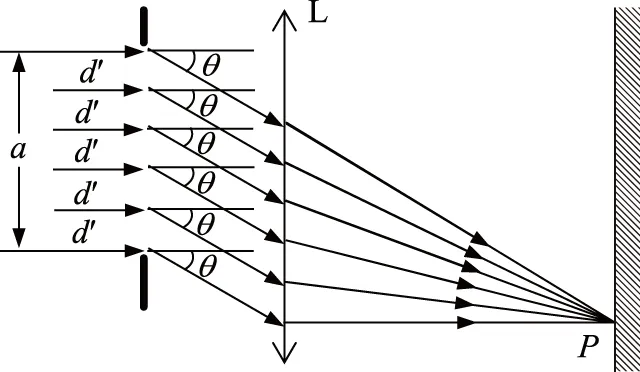
图5 夫琅禾费单缝衍射示意图
2 利用旋转矢量法讨论光的衍射
关于夫琅禾费衍射,文献[8]讨论了双缝、单缝和多缝的干涉和衍射光强分布曲线的计算;文献[9]针对处理菲涅尔-基尔霍夫衍射积分公式进行了讨论;文献[10]分析了衍射屏上光波相位分布对单缝衍射光强的影响;文献[11]讨论了菲涅尔半波带法、振幅矢量叠加法和积分定量计算法3种方法;文献[12]讨论了单缝衍射条纹公式及其条纹级次。利用菲涅尔半波带法讨论夫琅禾费衍射时,可以较为简洁地得到明暗条纹条件,但是不能给出光强分布;菲涅尔-基尔霍夫衍射积分公式超出了工科大学物理要求。而利用旋转矢量法计算光的夫琅禾费单缝衍射不仅可以完整给出明暗条纹条件和光强分布,而且可以使学生较为容易理解。
根据惠更斯-菲涅尔原理,衍射是无数列子波叠加的结果,因此单缝衍射可以看成是无穷多缝(N→∞)干涉问题。图5给出了缝宽为a的夫琅禾费单缝衍射示意图:一束光强为I0(振幅为A0)的光在狭缝a处的波振面上分割成N(N→∞)个相干子光源,每个子光源的振幅为A0/N,这个相干子光源在空间相干叠加。

(7)
P点(即屏幕上任意一点)合振动光波强度表达式为
(8)

(9)
光强的极值条件可由上式求导等于零得到
(10)
极值条件为: (1)β=0;(2)sinβ=0;(3)βcosβ-sinβ=0。
对于β=0:根据关系式β=πasinθ/λ可得到sinθ=0,则图4中“相邻两缝”传到P点的相位差Δφ=0。因此,β=0对应着中央极大值的位置及光强,根据式(9)可得
(11)
在此情况下也可借鉴图3(a)所示的旋转矢量叠加来计算此时P点的合振幅。在此情况下
(12)

(13)
对于βcosβ-sinβ=0:对应单缝衍射光强次级极大值的位置,此时有β=tanβ。解此超越方程可得β1=1.430π,β2=2.461π,β3=1.471π等。
由此可得分列于中央主最大两边的其他最大值(称为次最大)的位置为
(14)
表1给出了夫琅禾费单缝衍射中央主明条纹和次级明条纹的位置,并与菲涅尔半波带法给出的结果做了比较,两者的差别在于由本方法所获得结果与菲涅尔半波带法相比,次级极大值的位置稍微向中心偏移,当衍射级数增大时,两者结果趋于一致。同时,表1也给出了次级明条纹与中向明条纹的相对强度。可以看出,各次级明条纹的强度比中央明条纹小很多,且随着衍射级数的增加,条纹强度迅速降低。图6根据式(9)绘出了单缝衍射光强分布曲线。

表1 单缝衍射极大值位置及相对光强

图6 单缝衍射光强分布
对于光栅夫琅禾费衍射,其条纹效果是单缝衍射对多缝干涉的调制作用。此时,要考虑从每一个狭缝发出来的光的单缝衍射效应。在此情况下,将单个狭缝的光强I0替换成式(8)中的I,再代入多缝干涉光强分布公式(3)时,即可得到光栅衍射光强分布:
(15)

图7 光栅衍射光强分布(N=20,a=b)
图7以20缝的光栅衍射为例,并假定光栅常数a+b=2a(依据式(15),并取N=20,d=2a),绘出了光栅衍射光强分布。图7中虚线表示缝宽为a的单缝衍射,实线表示光栅衍射。从中可以看出,光栅衍射是单缝衍射和多缝干涉的总效果,多缝干涉受到单缝衍射的调制作用。
3 结论
从以上讨论可以看出,在讨论光的多缝干涉和单缝衍射问题时,利用旋转矢量法分析计算光强分布十分简洁,对于工科专业的学生而言比较容易理解。因此,针对工科专业学生而言,在讲授杨氏双缝干涉知识时,可利用旋转矢量分析杨氏双缝干涉的条纹和光强分布,再推广到多缝干涉(N>2)情况;在讲授光的衍射(单缝衍射和光栅衍射)相关知识时,可按教材中先讲单缝衍射再讲光栅衍射的顺序进行,先用菲涅尔半波带法对单缝衍射做半定量讨论,再利用旋转矢量法来分析计算单缝衍射(N→∞的多缝干涉)条纹及光强分布,最后讲授光栅衍射,循序渐进的讲授。一方面可以比较容易地引导学生总结出干涉和衍射这两个概念的区别与联系:从本质上来说,光的干涉和衍射都是光波相干叠加的结果,这是两者之间的共性;若不考虑每个狭缝的衍射调制效应,干涉是有限数量的光束之间由于光程差的变化而形成叠加效应,衍射是光波在传播中由于波阵面受到限制,光的传播偏离了原来直线传播的方向,使无穷多个次波之间产生了光程差而形成叠加效应,这是两者之间的主要差别;在实际中,干涉和衍射是同时存在的,在干涉条纹的计算过程中,通常是需要考虑缝的宽度不为零而造成的衍射调制效应,这样才能得到最为准确的干涉条纹分布,干涉和衍射的计算都是由惠更斯-菲涅尔原理为基础的,这是两者之间的联系。另一方面也可使学生对振动合成和光的干涉、衍射相关物理知识形成一脉相承的知识体系。
[1] 曲芳, 于意仲, 倪晓昌, 等. 浅谈启发式教学法在物理光学课堂教学中的应用[J]. 科教文汇:中旬刊. 2015(2):51-52. Qu Fang, Yu Yizhong, Ni Xiaochang, et al. A brief discussion on the application of heuristic teaching method in physical optics classroom teaching[J]. The Science Education Article Collects, 2015(2): 51-52. (in Chinese)
[2] 吐尔逊·买买提. 如何改善波动光学教学方法探讨[J]. 和田师范专科学校学报.2015(1):47-48. Tuerxun Maimaiti. A probe into improving teaching methods of wave optics[J]. Journal of Hotan Normal College, 2015(1): 47-48. (in Chinese)
[3] 朱家昆,肖海波,郭定和,等. 大学物理中光学教学的探究与思考[J]. 高教学刊. 2015(18):102-103. Zhu Jiakun, Xiao Haibo, Guo Dinghe, et al. The exploration and thinking on the teaching of optics in college[J]. Physics Journal of Higher Education, 2015(18): 102-103. (in Chinese)
[4] 王莉,鲁刚. 光的干涉和衍射探讨[J]. 高师理科学刊. 2009(3):92-95. Wang Li, Lu Gang. Discussed shallowly on light interference and light diffraction[J]. Journal of Science of Teacher’ College and University, 2009(3): 92-95. (in Chinese)
[5] 吕太国. 干涉和衍射的联系与区别[J]. 物理与工程. 2010(1):19-20. Lv Taiguo. Connection and difference between interference and diffraction[J]. Physics and Engineering, 2010(1): 19-20. (in Chinese)
[6] 屈双惠, 侯维娜, 杨志宏, 等. 光的干涉与衍射的区别与联系[J]. 石家庄学院学报. 2010(6): 86-90. Qu Shuanghui, Hou Lina, Yang Zhihong, et al. Difference and relationship between light interferencr and diffraction[J]. Journal of Shijiazhuang University, 2010(6): 86-90. (in Chinese)
[7] 杨植宗,段永法,刘洋,等. 光的干涉与衍射现象的物理本质[J]. 高师理科学刊. 2011(1):57-58. Yang Zhizong, Duan Yongfa, Liu Yang, et al. Discussed shallow on light interference and light diffraction[J]. Journal of Science of Teacher’ College and University, 2011(1): 57-58. (in Chinese)
[8] 沈犁理,钟寿仙,胥良. 双缝、单缝和多缝的干涉和衍射光强分布曲线的计算[J]. 云南师范大学学报:教育科学版. 1999(5):26-28. Shen Lili, Zhong Shouxian, Xu Liang. Calculation of interference and diffraction intensity distribution curves of double slit, single slit and multiple slit [J]. Journal of Yunnan Normal University(Teaching and Research on Chinese As A Foreign Language), 1999(5): 26-28. (in Chinese)
[9] 朱湘柱. 衍射积分公式的诠释与应用[J]. 高师理科学刊. 2007(3):94-97. Zhu Xiangzhu. An explanation and application for formulas of diffraction theory[J]. Journal of Science of Teachers’ College and University, 2007(3): 94-97.(in Chinese)
[10] 张明霞, 艾小刚. 夫琅禾费单缝衍射光强分析与探讨[J]. 湘潭师范学院学报:自然科学版, 2009(4): 17-20. Zhang Mingxia, Ai Xiaogang. Analysis and discussion of Fraunhofer slit diffraction intensity[J]. Journal of Xiangtan Normal University(Natural Science Edition), 2009(4): 17-20. (in Chinese)
[11] 姜丽娜. 单缝夫琅禾费单缝衍射光强分布的3种计算方法[J]. 辽宁科技大学学报. 2011(2): 123-128. Jiang Lina. Three calculation methods of light intensity distribution of single-slit Fraunhofer diffraction[J]. Journal of University of Science and Technology Liaoning, 2011(2): 123-128. (in Chinese)
[12] 王小平, 江键, 许佳捷. 波动光学条纹公式及其条纹级次的讨论[J]. 实验科学与技术. 2015(1): 4-5. Wang Xiaoping, Jiang Jian, Xu Jiajie. Discussion on fringe formulaand fringe order in interference and diffraction[J]. Experiment Science and Technology, 2015(1): 4-5. (in Chinese)
■
THE APPLICATION OF ROTATIONAL VECTOR IN INTERFERENCE AND DIFFRACTION OF LIGHT
Chen Xuewen Yao Xue Zhang Jiawei Chen Zhenya
(Department of Math and Physics, Chongqing University of Science and Technology, Chongqing 401331)
The rotational vector is a very convenient tool for discussing the combination of two or more than two harmonic vibrations. It is very simple, intuitive to analyze and calculate the intensity distribution of light interference and diffraction by using rotational vector, without needing to calculate the complex integral calculation, and the results obtained are consistent with the Fresnel diffraction integral formula’s results. At the same time, it is able to help the students to deepen their overall understanding of the harmonic vibration combination, interference and diffraction by using the rotational vector to discuss the interference and diffraction of light. In this paper, we use the rotational vector to discuss the fringe distribution and intensity distribution of light interference and single slit diffraction.
rotational vector; interference of light; diffraction of light; intensity distribution
2016-12-27;
2017-03-13
国家自然科学基金(11347024);重庆市教育委员会2105年度高等教育教学改革研究立项项目(153151);重庆市科委基金(2016jcyjA0336);重庆市教委基金(KJ1401313);重庆科技学院博士教授启动基金(CK2014B21);重庆科技学院重点项目培育基金(CK2015128)。
陈学文,男,副教授,主要从事物理教学与科研工作,研究方向为理论物理,kat820810@163.com。
陈学文,姚雪,张家伟,等. 旋转矢量在光的干涉和衍射中的应用[J]. 物理与工程,2017,27(5):56-60.

