关于不定方程Mx(x+1)(x+2)(x+3)=Ny(y+1)(y+2)(y+3)其中(M,N)=(5,11)和(6,11)
胡邦群
(重庆师范大学 数学科学学院,重庆 400047)
关于不定方程Mx(x+1)(x+2)(x+3)=Ny(y+1)(y+2)(y+3)其中(M,N)=(5,11)和(6,11)
胡邦群
(重庆师范大学 数学科学学院,重庆 400047)
主要运用Pell方程、递推序列、同余式及(非)平方剩余等一些初等方法,证明了不定方程Mx(x+1)(x+2)(x+3)=Ny(y+1)(y+2)(y+3),其中(M,N)=(5,11)和(6,11)无正整数解.
不定方程;整数解;递归数列
当(m,n)=1,m,n∈N*时,对形如mx(x+1)(x+2)(x+3)=ny(y+1)(y+2)(y+3)的不定方程已有不少研究工作[1-11].此处将运用递归数列的方法证明当(M,N)=(5,11)和(6,11)时,不定方程:
5x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)
(1)
6x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)
(2)
均无正整数解.
1 不定方程5x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)
先将方程(1)化为[5(x2+3x+1)]2-55(y2+3y+1)=-30
(3)
易知方程X2-55Y2=-30的全部整数解[12],由以下两个(非结合)类给出:

(2y+3)2=±4yn+5
(4)
易得出下列等式:
yn+1=178yn-yn-1,y0=1,y1=149
(5)
un+1=178un-un-1,u0=1,u1=89
(6)
vn+1=178vn-vn-1,v0=1,v1=12
(7)
(8)
yn=un+5vn
(9)
un+2h≡-un(moduh)n,vn+2h≡-vn(moduh),yn+2h≡-yn(moduh)
(10)
um+n=umun+55vmvn,vm+n=umvn+unvm,u-n=un,v-n=-vn
(11)
下面将证明式(4)仅当n=0时成立,由此求得方程(1)的全部整数解.
(2y+3)2=-4yn+5解的证明.考察式(4)的解,即n取何值时-4yn+5为完全平方数.
引理1 -4yn+5是平方数仅对n=0成立.
证明 从式(5)知道yn>1(n≠0),从而-4yn+5是负数,不可能为一个平方数.当n=0时,-4yn+5=1,结论成立.证毕.
2 解的证明
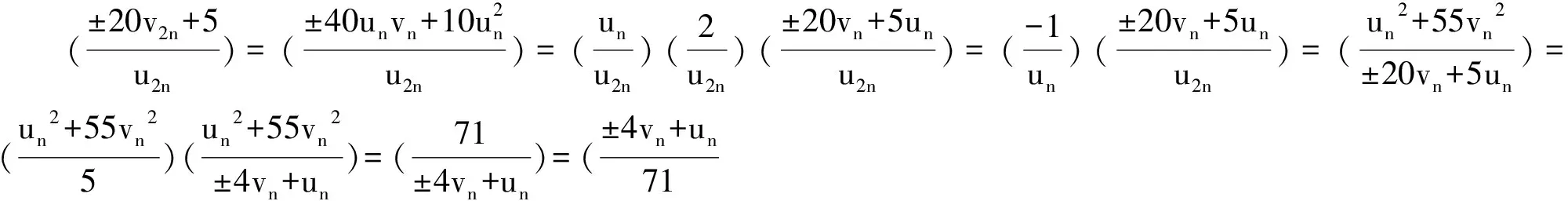
引理3 若4yn+5是平方数,则必须n≡0(mod150).
证明 采用对序列{4yn+5}取模的方法进行证明.
mod151,排除n≡2,3(mod5),此时4yn+5≡87,113(mod151).剩n≡0,1,4(mod5).
为了节省篇幅,每次仅给出每次取模所用的素数以及n的剩余类情况.取mod6301,剩n≡0,4,5,9(mod10).取mod521,剩n≡0,5,10,15,19(mod20).取mod199,149剩n≡0,30,40,50,60,80,85,90,99(mod100).取mod13,59,1289,2437,2699剩余n≡0(mod150)引理得证.
引理4 设n≡0(mod150),则仅当n=0时,4yn+5为平方数.
证明 若n=52×2t×k(t≥1,k≡1(mod2)),对序列{un+4vn}取模71得两个剩余序列周期为36,而对{2t}模36的剩余序列周期为6.对k分两种情况讨论:
1)当k≡1(mod4)时,当t≡0,1,2(mod6)时,令m=2t;当t≡3(mod6)时,令m=5×2t;当t≡5(mod6)时,令m=3×2t;当t≡4(mod6)时,令m=52×2t.则当t(≥1)(mod6)=0,1,2,3,4,5时,m(mod36)=28,20,4,4,4,24,对应{um+4vm}(mod71)=41,39,14,14,14,21,这些数均为模71的平方非剩余.再由式(9),(10)和引理2知:4yn+5≡20v2m+5(modu2m).

2)当k≡3(mod4)时,当t≡3,4,5(mod6)时,令m=2t;当t≡0(mod6)时,令m=5×2t;当t≡2(mod6)时,令m=3×2t;当t≡1(mod6)时,令m=52×2t,则当t(≥1)(mod6)=0,1,2,3,4,5时,m(mod36)=32,32,12,8,16,32,
对应序列{um-4vm}(mod71)=14,14,21,41,39,14,这些数均为模71的平方非剩余,由式(9),(10)和引理2知:4yn+5≡-4y2m+5≡-20v2m+5(modu2m).

2 不定方程6x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)
先将方程(2)化为[6(x2+3x+1)]2-66(y2+3y+1)=-30
(12)
易知方程X2-66Y2=-30的全部整数解[7],由以下两个(非结合)类给出:
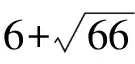
(2y+3)2=±4yn+5
(13)
易得出下列等式:
yn+1=130yn-yn-1,y0=1,y1=113
(14)
un+1=130un-un-1,u0=1,u1=65
(15)
vn+1=130vn-vn-1,v0=1,v1=8
(16)
(17)
yn=un+6vn
(18)
un+2h≡-un(moduh)n,vn+2h≡-vn(moduh),yn+2h≡-yn(moduh)
(19)
um+n=umun+66vmvn,vm+n=umvn+unvm,u-n=un,v-n=-vn
(20)
下面将证明式(13)仅当n=0时成立,由此求得方程(2)的全部整数解.
考察式(13)的解,即n取何值时-4yn+5为完全平方数.
引理5 -4yn+5是平方数仅对n=0成立.
证明 从式(14)知道:yn>1(n≠0),从而-4yn+5是负数,不可能为一个平方数.当n=0时,-4yn+5=1,结论成立.证毕.
2 (2y+3)2-4yn+5解的证明
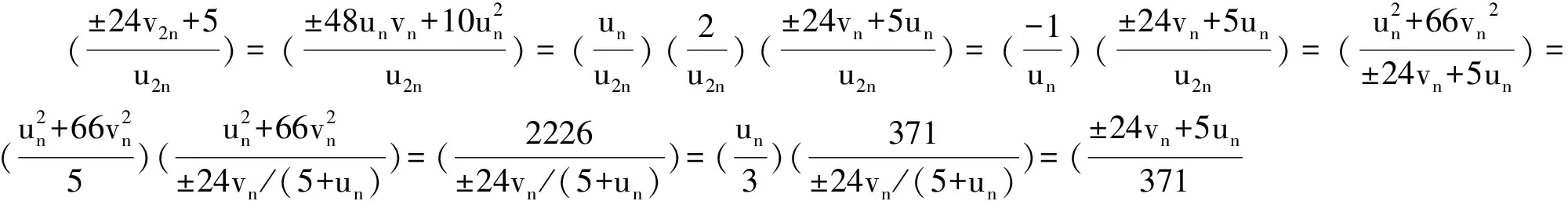
引理7 若4yn+5是平方数,则必须n≡0(mod60)
证明 采用对序列{4yn+5}取模的方法进行证明.mod17029,排除n≡1,2,3,4(mod5),此时4yn+5≡457,7674,8841,73(mod17029).剩n≡0(mod5).为了节省篇幅,每次仅给出每次取模所用的素数以及n的剩余类情况.取mod29,剩n≡0,5(mod15).取mod43,95881,剩n≡0,15(mod30).取mod1321,281剩n≡0,30(mod60).对n≡30(mod60),令n=60t0+30,若2|t0则n≡6(mod8).2⫮t0则n≡2(mod8).取mod7排除n≡2(mod8).对于n≡6(mod8)即n≡6,14,22(mod24)取mod23剩n≡22(mod24)即n≡22,46(mod48)取mod47排除n≡22,46(mod48).综上所述n≡0(mod60)引理得证.
引理8 设n≡0(mod60),则仅当n=0时,4yn+5为平方数.
证明 若n=2×5×3×2t×k,(t≥1,k≡1(mod2)),对序列{5un+24vn}取模371得两个剩余序列周期为104,而对{2t}模104的剩余序列周期为12.对k分两种情况讨论:
1)当k≡1(mod4)时,当t≡1,6,7,8,9,10(mod12)时,令m=2t;当t≡0,4,11(mod12)时,令m=5×2t;当t≡2,3,5(mod12)时,令m=3×2t.则当t(≥1)(mod12)=0,1,2,3,4,5,6,7,8,9,10,11时,m(mod104)=96,80,64,24,80,96,64,24,48,96,88,48.
对应{5um+24vm}(mod371)=82,264,278,152,264,82,278,152,250,82,355,250,这些数均为模371的平方非剩余.再由式(18),(19)和引理6知:4yn+5≡4y2m+5≡24v2m+5(modu2m)

2)当k≡3(mod4)时,当t≡0,1,2,3,4,7(mod12)时,令m=2t;当t≡5,6,10(mod12)时,令m=5×2t;当t≡8,9,11(mod12)时,令m=3×2t,则当t(≥1)(mod12)=0,1,3,4,5,6,7,8,9,10,11时,m(mod104)=40,80,56,8,16,56,8,24,40,80,24,8.
对应序列{5um-24vm}(mod371)=278,152,250,82,355,250,82,264,278,152,264,82,这些数均为模371的平方非剩余,由式(18),(19)和引理6知:4yn+5≡-4y2m+5≡-24v2m+5(modu2m)

3 结果
根据前面的讨论,现在给出本文的主要结果.
定理1 不定方程5x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)无正整数解.
证明 由引理1有:(2y+3)2=-4y0+5=1,故y=-1,-2.由引理4有:(2y+3)2=4y0+5=9,故y=0,-3.易知方程(1)共有16组平凡解:(0,0),(0,-1),(0,-2),(0,-3),(-1,0),(-1,-1),(-1,-2),(-1,-3),(-2,0),(-2,-1),(-2,-2),(-2,-3),(-3,0),(-3,-1),(-3,-2),(-3,-3)故不定方程5x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)无正整数解.证毕.
定理2 不定方程6x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)无正整数解.
证明 由引理5有:(2y+3)2=-4y0+5=1,故y=-1,-2.由引理8有:(2y+3)2=-4y0+5=9,故y=0,-3.易知方程(2)仅有16组平凡解:(0,0),(0,-1),(0,-2),(0,-3),(-1,0),(-1,-1),(-1,-2),(-1,-3),(-2,0),(-2,-1),(-2,-2),(-2,-3),(-3,0),(-3,-1),(-3,-2),(-3,-3)故不定方程6x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)无正整数解.证毕.
不定方程是数论中的一个重要分支,该领域在近几年有了一定的发展.但从整体来看,对于高于二次的多元不定方程,探索还不够.再者,不定方程与数学的其他分支诸如组合数学、代数数论、有限群伦、最优设计等有密切的关联,这使得更多数学家对不定方程产生了兴趣.上述不定方程是当代数学最重要的研究对象之一.
[1]COHNJE.TheDiophantineEquationx(x+1)(x+2)(x+3)=2y(y+1)(y+2)(y+3)[J].PacificJMath,1971,37:240-331.
[2] PONNUDURAI T.The Diophantine Equationx(x+1)(x+2)(x+3)=3y(y+1)(y+2)(y+3)[J].J London Math Soc,1975,10:232-240.
[3] LUO Ming.On The Diophantine Equationx(x+1)(x+2)(x+3)=6y(y+1)(y+2)(y+3)[J].Indian J pure appl Math,2001,1:3-7.
[4] 罗明,朱德辉,马芙蓉.关于不定方程3x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)[J].西南师范大学学报(自然科学版),2009,10(5):16-21.
[5] 郭凤明,罗明.关于不定方程x(x+1)(x+2)(x+3)=10y(y+1)(y+2)(y+3)[J].西南师范大学学报(自然科学版),2013,38(10):13-16.
[6] 张洪,罗明.关于不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3),D=21,23[J].重庆工商大学学院报(自然科学版),2015,32(7):56-60.
[7] 林昌娜,罗明,关于不定方程x(x+1)(x+2)(x+3)=34y(y+1)(y+2)(y+3)[J].西南师范大学学报(自然科学版),2016,41(4):10-14.
[8] 郑惠,杨仕椿.不定方程ax(x+1)…(x+r-1)=by(y+1)…(y+s-1)的正整数解[J].西南民族大学学报(自然科学版),2012,38(3):349-352.
[9] 管训贵.关于不定方程y(y+1)(y+2)(y+3)=4p2kx(x+1)(x+2)(x+3)[J].云南民族大学学报(自然科学版),2011,20(3):207-208.
[10] 程遥,马玉林.关于不定方程x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)[J].重庆师范大学学报(自然科学版),2007,24(3):27-30.
[11] 段辉明,杨春德.关于不定方程x(x+1)(x+2)(x+3)=19y(y+1)(y+2)(y+3)[J].四川师范大学学报(自然科学版),2009,32(1):60-63.
[12] 柯召,孙琦.谈谈不定方程[M].哈尔滨:哈尔滨工业大学出版社,1980:26-27.
责任编辑:时 凌
On the Diophantine EquationMx(x+1)(x+2)(x+3)=Ny(y+1)(y+2)(y+3)((M,N)=(5,11)and(6,11))
HU Bangqun
(School of Mathematical Sciences,Chongqing Normal University,Chongqing 400047,China )
Some elementary methods such as Pell equation, recursive sequence, congruence and quadratic residue (non -) are used to prove that the Diophantine equationMx(x+1)(x+2)(x+3)=Ny(y+1)(y+2)(y+3)((M,N)=(5,11)and(6,11)) has no positive integer solution.
Diophantine equation; integer solution; recurrence sequence
2017-03-01.
西南大学博士科研项目(20710903).
胡邦群(1991-),女,硕士生,主要从事代数数论的研究.
1008-8423(2017)03-0286-04
10.13501/j.cnki.42-1569/n.2017.09.009
O156. 2
A

