基于正交匹配追踪及加速近端梯度的人体三维重建

汪亚明 翟俊鹏 莫 燕 韩永华 蒋明峰

(浙江理工大学信号与信息处理研究所，杭州 310018)

基于正交匹配追踪及加速近端梯度的人体三维重建

汪亚明 翟俊鹏 莫 燕*韩永华 蒋明峰

(浙江理工大学信号与信息处理研究所，杭州 310018)

为提高人体三维结构的重建精度，针对重建过程中字典中原子的最佳选择和结构矩阵的优化问题，结合稀疏表示和低秩约束，提出一种正交匹配追踪追踪及加速近端梯度(OMP-APG)算法，以此为医学领域提供丰富的信息，以辅助医生快速精确地制定出治疗方案。首先，对特征点观测矩阵进行奇异值分解(SVD)分解，利用列文伯格-马夸尔特(LM)算法得到唯一确定的相机旋转矩阵；其次，利用稀疏表示中“最大化逼近”思想，通过正交匹配追踪算法对轨迹基系数进行求解，结合预定义的轨迹基求解出人体三维结构矩阵；最后，根据结构矩阵是一个低秩矩阵，将其秩优化问题转化为核范数最小化问题，利用加速近端梯度算法对人体结构矩阵进一步优化处理。将该算法与稀疏逼近算法进行比较，对伸懒腰、瑜伽、拾物、喝水和跳舞等5组不同的人体运动模型进行三维重建，通过其三维重建效果图和三维重建误差的结果显示，其重建精度更高且稳定性更好。在该算法下喝水运动的重建效果最佳，其1 102帧图像序列41个特征点的重建误差为0.030 3，而在稀疏算法下的重建误差为0.017 8。因此，该算法可以有效地提高人体三维结构的重建精度，为医学领域辅助治疗提供相应的技术支持。

三维重建；人体运动重建；稀疏表示；加速近端梯度

引言

利用二维图像序列来恢复人体三维结构成为近几年的研究热点，即寻找合适的算法从已知的二维序列观测点中恢复人体的三维结构[1-2]。在先前的研究中，Tomasz和Kanata提出利用观测矩阵的秩约束对观测矩阵进行因式分解(SVD分解)[3]，即在正交投影模型下结合观测矩阵的秩约束条件，对其进行SVD分解，利用非线性优化迭代方法求解矫正矩阵，进而恢复出目标物体的三维结构矩阵和相机旋转矩阵。随着研究的不断深入，Bregler 等人将SVD分解拓展到非刚性的三维重建上，提出形状基模型理论[4]。通过预定义形状基的线性组合来恢复非刚性运动的结构矩阵，从而将求解问题转化为求解形状基线性组合系数的问题。Akhter等人对形状基和形状空间进行了研究和扩展，结合非刚性运动的连续性和平滑特性，提出轨迹基模型[5]。同时，他们也对形状基和轨迹基之间存在的对偶性进行了论证，即形状基、形状基系数和轨迹基、轨迹基系数之间可以交换，其中形状基对应轨迹基系数，形状基系数与轨迹基相对应。人体三维重建从形状基到轨迹基的转变使得其研究更加进步。近期研究中，将信号恢复领域中稀疏思想[6-7]应用于三维重建，即利用稀疏思想来稀疏化表示轨迹基系数矩阵，然后再寻找一种求解稀疏度函数的算法来求解得到精确的轨迹基系数，从而提高三维结构矩阵的重建精度。但仍有不足之处，存在轨迹基中最优原子的选择问题和结构矩阵的优化问题，即尽量选择最佳的原子组合来表示轨迹曲线，以及进一步优化结构矩阵。本研究中所提及的OMP-APG算法，解决了轨迹基中原子的最佳选择和结构矩阵的最优恢复问题。

由于人体运动表现出非刚性，因此本研究是在轨迹空间[8-9]中展开研究的。首先，利用稀疏表示思想来稀疏化系数矩阵来降低大矩阵的求解难度。根据正交匹配算法(OMP)对轨迹基的系数进行求解，然后结合预先定义原子字典恢复出人体运动三维结构矩阵。求解得到的三维人体结构矩阵是一个低秩矩阵，由于秩函数稳定性不好，将其转化为秩的最小化问题。通常情况下，秩的最小化求解问题是一个NP难问题，因此将其放宽为核范数的最小化求解问题，可采用加速近端梯度算法来求解核范数最小化的问题，就是用正交匹配追踪算法求得的三维结构矩阵作为APG算法的迭代初值进行优化，经过迭代重建出精度更高的三维人体结构。

1 方法

1.1 人体三维重建结构

假设M表示人体运动图像的帧数，N代表每帧图像中人体上所取得的特征点数，则二维观测矩阵W可以表示为维数为2M×N的矩阵，形式如下：

(1)

式中：W矩阵是二维观测矩阵，是一个2M×N的矩阵；uij代表第i帧第j个点二维序列中的x坐标，vij代表第i帧第j个点二维序列中的y坐标。

根据因式分解理论以及轨迹基理论模型可以将人体重建的结构矩阵[10-11]表示为

(2)

式中，R是相机的旋转矩阵，Θ是预定义的原子字典，A是轨迹基系数，K表示轨迹线性组合个数。

结合SVD分解以及式(2)，可以得到人体三维结构矩阵的表达式为

(3)

式中，S代表人体运动的三维结构矩阵，K表示线性组合的轨迹基个数，Θ是经过函数变换得到的基，A表示对应的轨迹基系数。

1.2 OMP-APG算法

1.2.1 正交匹配追踪算法

稀疏表示[12]这一概念源自信号与系统领域，从一个给定的过完备集合中自适应的选出若干原子对原始信号进行逼近。根据稀疏定义和表示理论，可以列出稀疏表示的优化问题如下：

(4)

式中，f是任意信号，D是用于稀疏分解的过完备字典，范数‖c‖0定义为向量c中非零的个数。

由于l0范数是非凸范数，上述求解过程一个NP问题，故将优化问题转化为某种稀疏度函数进行求解。在信号系统领域稀疏表示的算法很多，如基追踪算法、正交匹配追踪算法、FOCUSS算法等。正交匹配追踪算法的优化问题是通过贪婪算法转化为求单个有限项的逼近问题。

(5)

(6)

有关定理[14]证明，正交匹配算法可以使逼近误差在有限迭代次数内(小于等于H空间的维数)衰减到零，而基本的匹配追踪算法不能保证这一点。

1.2.2 系数求解

对人体三维运动重建，需要首先确定相机旋转矩阵R[15]，才能进一步求解轨迹基系数。将W矩阵进行SVD分解，得到

(7)

因为一个非奇异Q矩阵的存在，使得式(7)分解出来不唯一的结果，即

(8)

式中，Λ=RΘ，A为轨迹基系数。

令Si=[Tx(i),Ty(i),Tz(i)],Si∈RM×3，表示在连续变化的M帧图像中的第i个特征点的运动轨迹在x、y、z各个方向上的坐标，即重建物体结构矩阵S中第i个连续的3列，故有

[Tx(i),Ty(i),Tz(i)]=

(9)

式中，Tx(i)、Ty(i)、Tx(i)分别代表第i个特征点在X、Y、Z三个方向上的轨迹集合，θi代表由函数产生的轨迹基，αi代表对应的轨迹基系数。

式(9)也能写成

(10)

结合式(2)中的W=RS和稀疏优化表达式(4)以及稀疏度函数概念，可以将轨迹基系数求解的稀疏优化问题转化为求解l1范数[16]，即

(11)

式中：wi表示人体运动的第i个特征点在M帧序列图像中的二维坐标，αi是相对应的轨迹基系数；Π=RΘ，其中R是相机的旋转矩阵，Θ是预先定义的原子字典。

本研究采用DCT基作为原子字典，结合估计出旋转矩阵R，利用正交匹配算法、根据式(11)求解出轨迹基系数A。该算法具体求解过程及算法步骤如文献[17]所示。

1.2.3 结构优化

基于正交追踪算法求解出轨迹基系数之后，结合预定义的原子字典，利用(10)恢复出人体三维结构矩阵S。由于S矩阵是一个低秩矩阵，因此可以利用秩约束对其进行优化求解。由于秩函数数值稳定性不好，所以将其转化成秩的最小化问题[18]，即

(12)

然而，秩的最小化求解通常是一个NP难问题。因此将秩的最小化放宽到核范数最小化，即min‖S‖*。再利用APG算法来求解核范数最小化问题[19]。将核范数优化最小化问题写成拉格朗日表示为

(13)

所以，式(13)可转化为

(14)

将上面求得的人体三维结构矩阵作为APG算法[20-21]的迭代初值，进一步优化得到高精度的人体三维结构矩阵。

1.3 算法步骤

如上所述，已知二维观测矩阵W∈R2M×N，根据因式分解理论以及稀疏表示思想等基础知识，整个人体三维重建过程以及算法步骤如下：

1)初始化。利用相机投影模型和真实三维结构矩阵初始化观测矩阵W，预定义DCT基作为轨迹基Θ。

2)求解旋转矩阵。利用SVD(因式分解法)对观测矩阵W进行分解，然后再结合相机旋转矩阵的正交约束条件，利用LM算法求得唯一确定的矫正矩阵Q，再根据式(8)求解出相机旋转矩阵R。

3)求解特征点运动轨迹系数。将特征点坐标按照帧序数依次排列，以某个特征点为单元，结合式(11)的稀疏表示思想，利用OMP贪婪算法顺序，寻找该特征点在轨迹基Θ下使得重构误差最小时的最佳轨迹线性组合系数矩阵Ai。

4)重建人体三维结构。结合预定义轨迹基Θ和上一步求得的系数矩阵Ai，利用式(10)恢复出第i个特征点的三维结构矩阵Si，经过N次迭代后求解整个运动所有特征点的三维结构矩阵S。

5)优化三维人体结构矩阵。求解时无需直接求解式(14)，而是求解其在某点处的一个二阶近似。具体将第4步求得的结构矩阵S作为APG算法迭代初值，优化得到更加精确的人体三维结构矩阵S。

1.4 算法评估准则

本算法性能主要由三维重建结构误差来衡量重建效果的好坏，也是重建后的结构矩阵与真实的三维结构之间的误差。为了对重建误差进行精确的评估，计算公式定义[22]为

(15)

(16)

(17)

(18)

(19)

式中：σtx、σty、σtz分别三维结构中第t帧对应的所有结构点X、Y、Z坐标的标准差(t=1,2,…,M；j=1,2,…,N)；etj表示第t帧第j个三维结构点的误差，即重构点与实际点间的欧氏距离；Sr代表重建出的三维结构矩阵，S0代表实际的空间结构矩阵，两者的维度和排列方式均完全相同。

(20)

1.5 验证方法

本研究所用实验数据来源于网站(http://cvlab.lums.edu.pk/nrsfm)中提供的5种人体运动，具体为包含370帧图像(每帧有41个特征点)的伸懒腰运动；包含307帧图像(每帧有41个特征点)的瑜伽运动；包含1 102帧图像(每帧有41个特征点)的喝水运动；包含357帧图像(每帧有41个特征点)的拾物运动；包含264帧图像(每帧有75个特征点)的跳舞运动。

为了验证所提出算法的有效性和可靠性，通过编程实验对上述5种人体运动进行三维重建。实验所用硬件配置为处理器Inter(R)@3.40 GHz 3.40 GHz，内存4 GB；软件环境为Window7，Matlab2010b。通过编程实验恢复出人体三维结构矩阵，然后利用公式(15)和公式(20)分别计算该算法下的重建点与真实点之间的重建误差和帧均误差，并绘制三维重建效果图对其进行算法评估和有效性分析。在实验中，将本算法与其他4种研究算法进行比较，对比的算法包括：MP[22]算法、PTA[5]算法、APG[21]算法和稀疏[15]算法，且以上4种算法所用实验数据与本算法来源于同一网站。

首先，对PTA算法、稀疏算法与本研究算法的重建帧均误差曲线进行比较，帧均误差曲线在图中所在的位置越低，说明该算法下的帧均误差越小，以此证明算法的有效性。其次，利用柱状图对5种人体运动在PTA算法、稀疏算法和本文算法下的重建误差进行对比分析。主要通过柱状块的高低来判断重建算法的可靠性，柱状块越低说明其重建误差数值越小，反映该算法下三维重建效果越好。然后，从视觉角度分析，绘制伸懒腰运动、跳舞运动和瑜伽运动在本研究算法与稀疏算法下的三维重建效果图。由于稀疏方法重建效果优于DCT方法，故仅列出本算法与稀疏算法的重建效果图进行比较。主要通过观察真实三维点与重建三维点之间的距离和吻合度来验证算法的有效性，真实点与重建点之间越吻合，说明该算法下的重建效果越好。最后，列出上述5种运动在不同算法下的三维重建误差数据对比表，表中数据数值越小，说明其重建误差越小，重建精度越高。通过对比重建误差表中数据的大小，验证本算法的有效可行性。

2 结果

图1为DCT方法、稀疏方法和本研究算法下的重建帧均误差曲线。可以看出，随着帧数变化，本算法下大多数帧的帧均误差曲线均在PTA算法和稀疏算法帧均误差曲线之下，仅有一小部分帧均误差曲线高于以上两种算法，说明该算法下的三维重建误差相比于其他两种算法大部分帧下都有所降低，验证了该算法具有一定的可行性。

图1 Stretch运动不同算法下重建的均方误差Fig.1 MSE of stretch motion under the different algorithms

图2为PTA算法、稀疏算法和本研究算法下对5种人体运动的重建误差柱状图。可以看出，对于不同的运动模型本算法的三维重建误差柱状块均低于前面两种算法，即该算法下的重建误差最小，证明该算法具有有效可行性。

图2 不同算法下五种运动的重构误差柱状图Fig.2 The reconstruction error histogram of five motions by different algorithms

图3～5分别为人体伸懒腰运动、跳舞运动和瑜伽运动的三维重建效果。可以看出，本算法下重建坐标点与真实坐标点之间的距离更近，说明其重建效果优于稀疏算法的重建效果，因此证明该算法的有效性和可靠性。

表1为5种人体运动在MP算法、PTA算法、APG算法、稀疏算法和本研究算法下重建的三维结构矩阵重建误差对比，其中括号中的数字表示最佳重建时所需轨迹基个数。由于MP算法、稀疏算法和本研究算法属于追踪算法，其每个特征点重建过程中都可以自适应选择轨迹基个数，且每个特征点寻找到的轨迹基个数不尽相同，因此此处无法对整体的重建列出轨迹基个数。可以看出，本算法的重建误差数值小于其他4种算法的重建误差数值，对伸懒腰运动、瑜伽运动和喝水运动重建误差相对较小，相比于稀疏方法分别提高了17.69%、14.12%、41.25%；对跳舞运动和捡物运动重建误差相对较大，与稀疏方法比较分别提高了9.58%和9.73%。以上数据说明该算法能够有效地降低重建误差和具有提高重建精度的能力。

图3 不同算法伸懒腰运动的三维重建效果(上为Sparse方法，下为本算法；“·”表示真实的三维结构点坐标，“°”代表重建出的三维结构点坐标；方框中为重建效果较好的特征点)。(a)第20帧; (b)第130帧; (c)第260帧; (d)第310帧Fig.3 3D reconstruction renderings of stretch motion with different methods(The above is sparse method, the below is this algorithm; “·”represents the real 3D structure point coordinates, “°”represents the reconstruction 3D structure point coordinates. The point in box is the better features of reconstruction). (a) The 20th frames; (b)The 130th frames; (c)The 260th frames; (d)The 310th frames

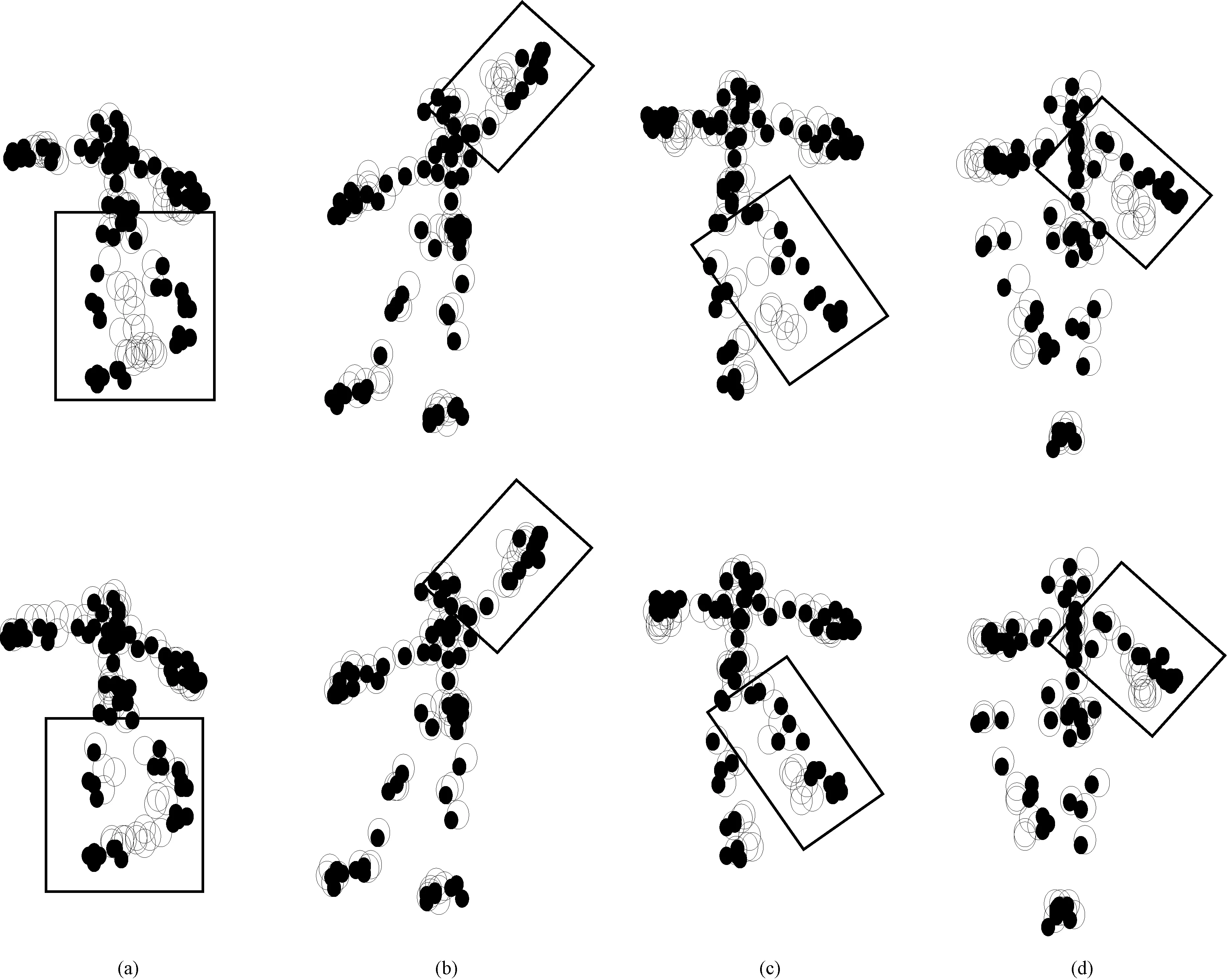
图4 不同算法跳舞运动的三维重建效果(上为Sparse方法，下为本算法；“·”表示真实的三维结构点坐标，“°”代表重建出的三维结构点坐标；方框中为重建效果较好的特征点)。(a)第10帧; (b)第60帧; (c)第130帧; (d)第210帧Fig.4 3D reconstruction renderings of dance motion with different methods(The above is sparse method, the below is this algorithm; “·”represents the real 3D structure point coordinates, “°”represents the reconstruction 3D structure point coordinates. The point in box is the better features of reconstruction). (a)The 10th frames; (b)The 60th frames; (c)The 130th frames;(d)The 210th frames

图5 不同算法瑜伽运动的三维重建效果(上为Sparse方法，下为本算法；“·”表示真实的三维结构点坐标，“°”代表重建出的三维结构点坐标；方框中为重建效果较好的特征点)。(a)第50帧; (b)第100帧; (c)第225帧; (d)第280帧Fig.5 3D reconstruction renderings of yoga motion with different methods(The above is sparse method, the below is this algorithm; “·”represents the real 3D structure point coordinates, “°”represents the reconstruction 3D structure point coordinates. The point in box is the better features of reconstruction). (a)The 50th frames; (b)The 100th frames; (c)The 225th frames; (d)The 280th frames

表1 不同算法对各种人体运动的重建误差(其中括号中的数字表示最佳重建时所需轨迹基个数)

Tab.1 Error table of various human motion in different algorithms (The number in parentheses indicates the number of trajectories needed for optimal reconstruction)

实验模型MPDCTAPGSparse本方法伸懒腰0.85490.1088(12)0.1071(12)0.08930.0735瑜伽0.80390.1622(11)0.1620(11)0.15580.1338拾物0.43320.2369(12)0.2341(12)0.22450.2030喝水0.46040.0250(13)0.0219(13)0.03030.0178跳舞0.26390.2958(5)0.2669(5)0.25190.2274

3 讨论和结论

本研究利用正交匹配追踪及加速近端梯度算法对人体三维运动进行重建，根据帧均误差、重建误差和重建效果对实验进行分析。由表1中重建误差的数据显示，本算法下5组人体运动的重建误差均有不同程度的减小，由此可见，本算法最优，PTA算法最差，稀疏算法次优。其根本原因在于PTA算法中，主要利用伪逆法求解轨迹系数，整个过程是纯粹的矩阵运算，这样不仅加大了计算的复杂度，而且增加了求解大矩阵过程中未知参数的个数，并且其求解所得到的系数是稠密的，还存在需要人为尝试确定轨迹基个数的缺点，因此其重建效果最差。在稀疏算法中，虽然可以自适应选择基原子去拟合运动轨迹，重建出效果较好的人体三维结构，但求解系数过程中所用基追踪算法相对复杂，并未考虑结构矩阵自身是低秩矩阵的这个约束条件，因此该算法仍然存在不足。本算法继承了稀疏逼近算法中的自适应选择原子的优势，通过正交匹配追踪算法去顺序选择基原子来“最大化逼近”特征点运动轨迹，克服了人为确定轨迹基个数和计算复杂的缺点；同时结合三维结构矩阵低秩约束条件，将其秩最小化问题转化为核范数最小化问题，利用APG算法对结构矩阵进行优化处理。由实验效果可知，针对同一种运动模型本研究算法效果最佳，特别是人体手臂和腿部等细节部位的重建效果优于文献[5]中PTA算法和文献[15]中稀疏算法(见图3～5)，这是因为本算法具有自适应选择基原子和低制约束的双重制约，具有一定处理复杂运动的能力，使重建出的三维结构矩阵与真实的三维结构矩阵更加接近。根据上述对3种算法的分析和讨论，可以看出，影响人体三维重建精度的两大重要因素是原子字典的选择和轨迹系数的求解。选择合适的原子字典不仅可以减少计算复杂度，同时也可以提高重建的精度；同样，求解精确的轨迹系数，也可以达到降低重建误差的目的。本算法可以自适应在字典中选择最优原子，尽最大限度去逼近真实的三维结构，尤其对复杂运动和细节部位的恢复具有较好的稳定性。与文献[21-22]相比，其重建效果和重建误差均表明了本算法的优越性，但是由于DCT基自身原子种类不足的限制，只能在该基下选择最佳的原子进行逼近，从而无法最大逼近特征点的真实轨迹。因此，寻找更加完善的原子字典和求解更加精确的轨迹基系数，成为进一步深入研究的问题。

为了更好地提高人体三维结构的重建精度，本研究提出了一种正交匹配追踪加速近端梯度算法来解决人体三维运动重建问题，主要解决系数的求解和结构矩阵的优化问题。利用OMP算法对系数进行稀疏求解，从而达到基原子的最佳选择和利用APG算法对人体三维结构矩阵进行优化。通过相关实验数据，以Drink运动为例，用Sparse重建出的人体三维结构矩阵重构误差为0.030 3，通过本研究算法重建的重构误差为0.017 8。并且该算法同样适用于其他人体运动，结果表明，该算法具有良好的稳定性且可以有效提高重建精度，具有有效可行性。由于本研究是在固定原子字典的基础上研究的，字典中的原子数量和种类均受到限制。为了更加完整地表示特征点运动轨迹，今后将研究重心转移到原子字典的类型选择和优化上。

(致谢：在此对实验室成员张静、童朝凯和周志湖表示感谢，感谢他们在研究中对参考文献选择给予的指导，感谢他们在论文撰写中对写作思路给出的建议，还要感谢他们与我一起解决研究中的疑难问题和理论难题)

[1] Fabio R. 3-D reconstruction of static human body shape from image sequence[J]. Computer Vision and Image Understanding, 2004, 93(1): 65-85.

[2] Moeslund TB, Granum E. A survey of computer vision-based human motion capture[J]. Computer Vision and Image Understanding, 2001, 81(3): 231-268.

[3] Tmoasi C, Kanade T. Shape and motion from image streams under orthography: a factorization method[J]. International Journal of Computer Vision, 1992, 9(2): 137-154.

[4] Bregler C, Hertzmann A, Biermann H. Recovering non-rigid 3D shape from image streams[C] //Proceedings of IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Hilton Head: IEEE, 2000, 2: 690-696.

[5] Akhter I, Sheikh Y, Khan S, et al. Trajectory space: A dual representation for nonrigid structure from motion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(7): 1442-1456.

[6] Barthelemy Q, Larue A, Mars J. Decomposition and dictionary learning for 3D trajectories[J]. Signal Processing, 2014, 98: 423-437.

[7] Zhu Yingying, Simon L. Convolutional sparse coding for trajectory reconstruction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 529-540.

[8] Park HS, Shiratori T, Matthews I, et al. 3D reconstruction of a moving point from a series of 2D projections[C] //2010 IEEE European Conference on Computer Vision. Berlin: Springer-Verlag, 2010, 6313: 158-171.

[9] Park SH,Shiratori T, Matthews I, et al. 3D trajectory reconstruction under perspective projection[J]. International Journal of Computer Vision, 2015, 115(2): 115-135.

[10] Bue AD, Smeraldi F, Agapito L. Non-rigid structure from motion using non-parametric tracking and non-linear optimization[C] //2004 Conference on Computer Vision and Pattern Recognition Workshop(CVPRW). Washington: IEEE, 2004: 8-8.

[11] Zhu Yingying, Cox M, Simon L. 3D motion reconstruction for real-world camera motion[C] //2011 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Colorado Springs: IEEE, 2011, 8: 1-8.

[12] Vore D, Ronald A. Nonlinear approximation[J]. Acta Numerica, 1998, 7: 51-150.

[13] Mallat S, Zhang Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.

[14] Pati Y, Rezaiifar R, Krishnaprasad PS. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C] //Proceedings of 27th Asilomar Conference on Signals, Systems and Computers. Los Alamitos: IEEE, 1993: 40-44.

[15] Wang Yaming, Yan Xiaomeng, ZhengJ B, et al. Sparse approximation for nonrigid structure from motion[J]. Journal of Robotics, 2015, 3: 1-8.

[16] Chen Mingyu, Alergib G, Juang BH. Trajectory triangulation: 3D motion reconstruction with1 optimization[C] //2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Prague: IEEE, 2011: 4020-4023.

[17] Sahoo S, Makur A. Signal recovery from random measurements via extended orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2015, 63(10): 2572-2581.

[18] Silvia G, Isao Y. Alternating minimization techniques for the efficient recovery of a sparsely corrupted low-rank matrix[C] //2010 IEEE International Conference on Acoustics, Speech and Signal Processing. Dallas: IEEE, 2010, 6: 3638-3641.

[19] Trémoulhéac B, Atkinson D, Arridge SR. Fast dynamic MRI via nuclear norm minimization and accelerated proximal gradient[C] //2013 IEEE 10th International Symposium on Biomedical Imaging. San Francisco: IEEE, 2013: 322-325.

[20] Yue Lu, Zhang Liwei. The augmented Lagrangian method based on the APG strategy for an inverse damped gyroscopic eigenvalue problem[J]. Computational Optimization and Applications, 2015, 62(3): 815-850.

[21] Wang Yaming, Tong Lingling, Jiang Mingfeng, et al. Non-rigid structure estimation in trajectory space from monocular vision[J]. Sensors, 2015, 15(10): 25730-25745.

[22] Paladini M, Del Bue A, Stosic M, et al. Factorization for non-rigid and articulated structure using metric projections[C] //2009 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Miami: IEEE, 2009: 2898-2905.

3D Reconstruction of Human Body Based on Orthogonal Matching Pursuit and Accelerated Proximal Gradient

Wang Yaming Zhai Junpeng Mo Yan*Han Yonghua Jiang Mingfeng

(ResearchInstituteofSignalandInformationProcessing,ZhejiangSci-techUniversity,Hangzhou310018,China)

In order to improve the reconstruction accuracy of the 3D structure of human body, the optimal selection of atoms and the optimization of structure matrix in the process of reconstruction were investigated in this work. On the basis of the sparse representation and low-rank constraint, we proposed an orthogonal matching pursuit and accelerated proximal gradient (OMP-APG) algorithm to provide a wealth information to assist medical doctors to work out the treatment plan quickly and accurately. First of all, the feature matrix was decomposed by singular value decomposition (SVD), and the uniquely determined camera rotation matrix was obtained by LM (Levenberg-Marquardt) algorithm. Secondly, according to the idea of “maximization approximation” in sparse representation, the trajectory basis coefficients were solved by orthogonal matching pursuit algorithm, combined with a predefined trajectory basis to solve the 3D structure of the human body matrix. Finally, considering that the structure matrix was a low rank matrix, the rank optimization problem was transformed into the nuclear norm minimization problem, and the human body structure matrix was further optimized by the accelerated proximal gradient algorithm. The algorithm and sparse approximation algorithms were compared in five motion models including stretch, yoga, pick up, drink and dance in 3D reconstruction with the 3D reconstruction renderings and 3D reconstruction errors. The results showed that the reconstruction accuracy was higher and had better stability. In this algorithm, the reconstruction of drink motion was the best, and the reconstruction error of the 41 feature points of the 1102 frame image sequence was about 0.0303, while the reconstruction error under the sparse algorithm was about 0.0178. In conclusion, the algorithm improved the reconstruction accuracy of the human three-dimensional structure.

3D reconstruction; human motion reconstruction; sparse representation; accelerated proximal gradient

10.3969/j.issn.0258-8021. 2017. 04.001

2016-09-27， 录用日期:2017-01-08

国家自然科学基金项目(61672466)；浙江省自然科学基金(LZ15F020004，LY1720034)；浙江理工大学521项目

R318

A

0258-8021(2017) 04-0385-09

*通信作者(Corresponding author)，E-mail: moyan@zstu.edu.cn