重视反思,提高学习效率
文/潮州市湘桥区城基中学 林红铿
重视反思,提高学习效率
文/潮州市湘桥区城基中学 林红铿
培养学生对学习过程进行反思的习惯,提高学生的自我评价水平,是提高学习效率,增强创新能力行之有效的方法。例如,学生在解答数学题时,如果在获得正确答案后,不对解题过程进行回顾和反思,那么解题活动就有可能只停留在经验水平上,事倍功半;如果在每一次解题以后都能对自己的思路作自我评价,探讨成功的经验或失败的教训,那么就可促使学生的思维进入理性认识阶段,事半功倍。因此,为了提高学生的数学学习效率,必须引导学生养成反思的习惯。
在反思问题的设置上,我从以下几个方面进行了尝试。
1.反思解题关键,促使思维精确化、概括化
为提高解题质量和效率,引导学生回顾和整理解题思路,概括解题思想,使解题过程清晰化,思维条理化,精确化和概括化。
例1.已知梯形ABCD中,AD//BC,AB=CD,求证∠B=∠C,∠A=∠ADC。
因为要证明角相等,学生会依据 “等边对等角”“三角形全等”等定理证明,而本题是一个梯形,缺少运用上述定理所需的条件。学生通过各种尝试活动,获得问题解答以后,教师要求学生回顾解题过程,在反思过程中,应强调证明的关键是什么。通过学生的讨论和总结得到证明的关键是将梯形转化成三角形或平行四边形,即过点D作DE//AB,交BC于点E,把等腰梯形转化为▱ABED和等腰△DEC,经过这样的概括,解题思路就有条理了。此时,学生根据上述归纳的证题关键很容易就想出另两种添辅助线的方法,即分别从A、D作AE⊥BC,DF⊥BC垂足分别为E、F,把梯形分成两个直角三角形和一个矩形,或延长BA,CD,使它们相交于点E,把梯形转化为两个等腰三角形。
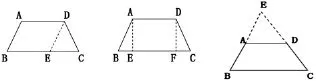
图1
2.反思思维策略,使学生掌握数学基本思想方法
在解题后让学生反思解题过程,分析具体方法中所包含的数学基本思想方法,对具体方法进行再加工,从中提炼出一般的数学思想方法。
例2.正三角形ABC内接于⊙O,D是弧BC上的一点,连结BD,CD,求证:BD+CD=AD。

图2
如图2(1),在AD上取AE=CD,连结BE,出示图2(2),引导学生延长DB,使DE=DA,连结AE,给出了证明。之后,让学生反思得出这两种解法的思想方法是什么呢?学生经过反思得出把两条较短的线段补成DE,然后证明DE=DA,或把长的线段AD截成两条短的,使其中一条等于BD(或CD),然后证明另一条等于CD(或BD)。这一反思过程使学生深刻地理解了证明 “两条线段的和等于一条线段”的问题的关键是问题转化成 “两条线段相等”的问题,体现了数学中化归的思想方法。
3.反思问题本质,使思维的抽象程度不断提高
解决问题以后再重新剖析问题的实质,可使学生抓住问题的实质,从中寻找它们之间的内在联系,探索一般规律,可使问题逐渐演化。例如,学生解决了“四边形的内角和等于360°”以后,要求学生反思求四边形的内角和的规律并探讨能否求出五边形,六边形……,n边形的内角和,经过讨论学生得出,求五边形,六边形甚至n边形的内角和的规律是将n边形分成 (n-2)个三角形,从而得出一般n边形内角和是 (n-2)180°。
4.反思解题方法,优化解题过程,寻找解决问题的最佳方案
学生在解题时,经常出现解题过程单一,思路狭窄,逻辑混乱,叙述冗长,主次不分等问题,这是学生思维过程缺乏灵活性、批判性的表现,也是学生的思维创造性水平不高的表现。因此,教师必须引导学生能评价自己的解题方法,努力寻找解决问题的最佳方案。通过这一评价过程,开阔学生的视野,使学生的思维朝着灵活,精细和新颖的方向发展。
例3.已知如图3,▱ABCD中,E、F是对角线AC上两点且AE=CF。
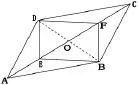
图3
求证:四边形DEBF是平行四边形。
在证明中学生习惯于依据三角形全等定理证明。证明过程虽无错误,但证明过程冗长,其原因是没有恰当运用平行四边形的判定定理。在教师的引导下,学生有可能给出如下证明。
连结BD,支AC于点O,
∵ABCD是平行四边形,
∴OB=OD,OA=OC。
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF。
四边形DEBF是平行四边形。
5.反思错误原因,使学生更加深刻地理解基础知识
教师应当重视结合学生作业中出现的错误设计教学情境,使学生在纠正作业错误的过程中对基础知识加深理解。
例如,一个圆锥的侧面展开图半径是18厘米,圆心角为240度的扇形,求这个圆锥的高线长。
学生在作业中常出现把半径为 “18厘米”误以为是圆锥的底面半径。其原因是学生对于圆锥的侧面展开图中的半径与圆锥的母线之间的关系理解不够深刻。此时教师应引导学生通过观察,分清圆锥侧面展开图中的半径就是圆锥的母线,从而纠正了错误。
总之,在数学教学中,重视培养学生对学习过程进行反思的习惯,可以启发学生不要受传统思维模式的束缚,从多角度,多侧面,多结构的思维方向去研究问题,寻求解决问题的最佳方案。实践证明,这样教学方式,深受学生欢迎。它不但激发了学生浓厚的兴趣,使学生在每道题出示后处于跃跃欲试的心理状态,而且打开了学生的眼界,拓宽了学生的思维途径。这对于提高学生学习效率是有裨益的。
责任编辑 邹韵文

