基于小学生数学思维能力培育的教案设计策略
聂岸义唐 理
湖南/ 湖南/
基于小学生数学思维能力培育的教案设计策略
聂岸义*唐 理*
关注学生的数学思维能力培育,不仅是新课程标准的基本要求,也是新时期学科素养培育的重要范畴。新课程改革认为,数学教学的核心是数学思维能力的培养。数学教师在进行教案设计时,应当把学生的思维能力培育作为教案设计的重要指导思想加以贯彻,并具体落实到教学中。
思维能力;小学生;设计策略
对于小学生的数学教学,应注重对他们的数学思维能力培养。关注学生的数学思维能力培育,不仅是新课程标准的基本要求,也是新时期学科素养培育的重要范畴。数学教学的核心是数学思维能力的培养,数学教师在进行教案设计时,应当把学生的思维能力培育作为设计的重要指导思想加以贯彻。[1]现结合小学数学教学,谈谈基于小学生数学思维能力培育的教案设计策略。
一、注重巧妙设疑,导引学生进行有效思考
正确的思维能力培养过程,要求教师在教学中设疑、解疑、质疑、拓展。对于小学生数学教案的设计,就要善于设疑,促进学生不断地思考,在思考的过程中获得思维能力的提升。笔者在苏教版教科书12册第14-16页中有关“成正比例的量”的教案设计中,为使学生理解正比例的意义,根据正比例的意义判断两种量是不是成正比例,探索正比例意义的教学活动,使学生感受事物中充满着运动、变化的思想,就注重设疑,促进学生进行有效思考,设计了一个“例5”的教学内容是:用600张纸装订同样的练习本,每本的张数和装订的本数有什么关系?请学生填写下表:
与此同时,引导学生思考:(1)表中有哪两种量?(2)装订的本数是怎样随着每本的张数变化的?表中的两种量是每本的张数和装订的本数,它们是相关联的量,装订的本数是随着每本张数的变化而变化。每本的张数扩大,本数反而缩小,每本的张数缩小,装订的本数反而扩大。但每本的张数和装订的本数的积总是一定的,都是600,它们的关系可以写成:每本的张数×装订的本数=总张数(一定)。这样学生就获得了相应的思维训练。
二、注意数量关系,导航学生基于生活解题
小学生数学思维能力提升,来自于对应用题教学的多元思考。数学教案的设计,可引导学生多角度、多层次地进行思考数学问题,尤其是与生活的结合,这样更容易让学生接受。[2]学生解答应用题的关键在于要有明确的解题思路。因此,在教案设计时,教师必须抓住数量关系给学生展示思维的方法和步骤,让学生在学会寻找数量关系,明确思路的过程中,掌握解题方法。在应用题教案设计中,可以从弄清题意→分析数量关系→列式计算→检验作答四个步骤。
首先要弄清题意,设计教案时可采用摘录法和线段图来明确已知条件和问题的方法,让学生轻易地弄清题意;然后,引导学生分析数量关系。弄清题意后,要找出问题与已知条件之间的关系,是解答应用题的关键,因此,在解题应用题时必须有着清晰的解题思路,也就是先解什么,再求什么的问题,教师在教学时,应尽量教给学生方法:“授人以鱼,不如授人以渔”,要帮助学生(在解决中间问题)弄明白为什么必须求出它才行,具体操作如下:①综合法。综合法分析数量关系,找出中间问题,对一般的学生很难理解和掌握,因此在讲此方法时,只稍微提示让学习成绩较优异的学生去自己体会。②分析法。分析法是由问题推出已知的方法,在推出过程很容易找出中间问题,自然学生的解题思路就清晰。第三是列式计算。学生在列式时,往往出现很多错误,如分步算式列式时单位混淆,综合算式掉括号等现象,这就要在平时训练解答应用题弄清什么问题,不能让学生糊涂。为了更好完成教学任务,必须在初级阶段写出解题计划。最后是检验作答。应用题列出算式得出结论而不够,而应该想一想到底此结论是否正确,因此检验作答此环节也不可少。这样学生就可以按照步骤去检查,亦可以把已知条件看作问题,把其中的一个已知条件中作问题来检验,数学思维能力在这个过程中就得到了提升。
三、注入情境元素,导诱学生积极求索
小学数学教学内容相对比较枯燥,教师在教案设计中要善于通过创设情境将抽象的内容具体化、形象化,吸引学生的学习兴趣,激发学生的求知欲望,加深对所学知识的理解。笔者在“成正比例的量”这一内容的教案设计中,就关注情境元素的融入,促进学生积极探求数学知识。在对苏教版教科书12册第11-13页成正比例的量的教案设计中,为使学生理解正比例的意义,能根据正比例的意义判断两种量是不是成正比例;通过讨论,探索正比例意义的教学活动,使学生感受事物中充满着运动,变化的思想,并且特定的事物发展,变化是有规律的。在设计教案中,我引入生活中买卖布的情境元素进行设计,讲解了这个例题:“在一间布店的柜台上,有一张写着某种花布的米数和总价的表如下:
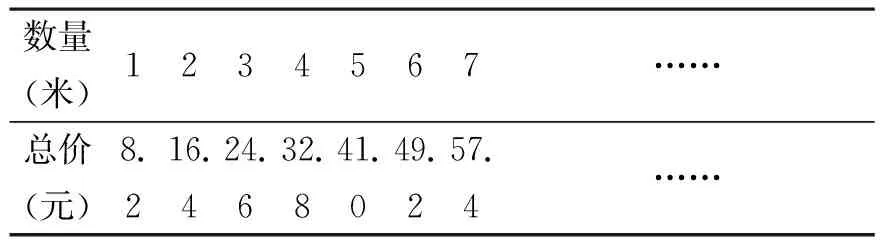
数量(米)1234567……总价(元)8.216.424.632.841.049.257.4……
在教案中设置了三个问题:(1)表中有哪两种量?(2)总价是怎样随着米数变化的?(3)相对应的总价和米数的比各是多少?比值是多少?通过讨论引导学生进行汇报交流,例2中的两种量是花布的米数和总价,它们是两种相关联营的量,米数扩大,总价也随着扩大,反之,总价也随着缩小,总价和米数的比值(单价)总是一定的。基于此,引导学生进一步明确两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。通过生活情境的引入,学生的思考就更活跃了。从学生已有的知识、生活经验出发,引出比例关系,接着引导学生观察、思考、讨论、分析路程与时间,总价与米数之间的变化规律,逐步理解正比例意义。这样,学生在和谐的学习群体中,经过思考、交流、探索的学习过程,学得生动活泼。
四、注明信息统整,导学数学媒体运用
小学生数学思维能力的提升,是与时代发展、信息发展紧密结合的,也强调在数学教学中融入现代数字技术、信息技术,促进学生用好数学媒体,促进信息素养的提升。在小学数学教学活动中,利用电教媒体创设情景,能将抽象单调的计算具体形象化,具有形象、模拟再现等优点。它以非智力因素为引导,较多地激发了学生的学习兴趣,提高课堂教学质量,促进学生智力因素的发展。在教案设计中,要善于将信息技术融入,激发学生的数学学习兴趣。[3]学生学习教学是一种有意义的行为,需要用学习教学的动机去激励他们、推动他们,这种动机可能是外部动机——来自家长、老师的教导、奖惩等,但最重要的是内部动机——学生对数学知识的向往和用学到的数学知识、技能解决问题的乐趣。电教媒体让学生惊奇、疑惑、具新鲜感,从而激发学生主动探索问题的动机。例如教学“运用商不变的规律进行有余数除法”的简便计算时,我边用电脑出示画有小猴、八戒、大圣的画面,并配有录音,讲述一个八戒分桃的故事:有一天,30只小猴到花果山上摘桃子,他们共摘了100只桃,正在他们为怎么分发愁的时候。猪八戒来了,小猴忙请八戒分桃。猪八戒眼珠一转,忙说:“好办,好办。”于是他先列式,然后运用商不变的规律计算。算完后他说,你们每只小猴分3只还余1个,这剩下的1个就归我了。小猴都表示同意,正当每只小猴分了3只桃兴高采烈地准备回家时,孙大圣来了,他一看八戒列的算式和计算过程,再看看小猴们手中的桃,顿时怒上心头,抡起金箍棒就打八戒,这下把小猴们给弄糊涂了。你知道为什么?随着上述情境的不断展开,学生趣味盎然,悬念顿生,思维处于欲罢不能的状态。
为促进小学生数学思维能力的培育,将信息技术融入到教学中去,在教案设计中将关注用信息技术突破数学计算中的重点和难点。现代教学手段,以其鲜明的色彩、形象的动画以及悦耳的声音,不仅能激发学生的兴趣,而且能激发老师教学兴趣。对于小学生来说,从老师提供的事例中归纳出一个法则、抽象出一个概念,想出一个巧妙的解法,都意味着一个发现,这对学生来说是难能可贵的,是创新思维的嫩芽。而保证这一嫩芽成长的有效手段,就是利用现代教育技术灵活多变的优势,为学生提供丰富的问题情境,提供交流的机会。比如,在计算“104×25”这题时,我将这题所想到的几种解法输入电脑,编上序号。在学生汇报时,根据不同的回答,点击前面的序号,则屏幕上就出现了不同的解题方法。在出现每题的解法时,将变化了的数运用闪动的方式,进一步让学生明白算理,培养思维的灵活性。利用信息技术媒体,既省时又省力,同时训练了学生采用多种策略的能力,并通过比较、鉴别,筛选出较优的解题策略,充分发挥了他们的创造性。
两种除法是低段教学中的一个难点,为了帮助学生理解两种分法的不同含义正确地区分两种分法,建立正确合理的知识结构,教师在导引学生初步学习了两种分法后,运用课件提供在容量的对比题组,作为学生思维整合、获取知识信息的感知材料,通过思维过程的对比展现,强化学生逻辑性思维的整合度,努力实现综合贯通,形成知识结构网络。屏幕上,伴随一阵欢快的音乐出现一棵大树,大树下挂着一个大鸟笼,在一片叽叽喳喳声中飞来10只小鸟,在5只同时飞进鸟笼后,图下出现两种不同的算式:10÷2=5(只),10÷5=2(次)。要求学生从中选择一个算式,若选择正确,就会出现小鸟们欢快跳跃的画面,并发出悦耳的叫声,若选择错了,小鸟们更会发出“错了”的叫声。及时评价与纠正后,教师操作课件,10只小鸟2只2只地飞进鸟笼里,然后让学生选择表示小鸟飞进鸟笼次数的算式。
在教案设计中,注重小学生思维能力培育,需要教师不断更新自己的教案,把数学生活情境融入其中,借助信息技术将数学教学的课堂呈现出立体化的发展态势,持续克服教案设计的单调性以及改变在教学和训练上的方法单一、陈旧、学生不感兴趣等弊端,这样才能提高课堂教学效率和教学质量,不断推进小学生数学思维能力的提升。
[1]周蔚,刘爱亮.新课程下小学生数学思维能力的培养[J].现代阅读,2013(11):241-242.
[2]魏忠海.小学生数学思维能力的培养[J].基础教育研究,2013(4):37-38.
[3]郭成.元认知训练对小学生数学问题解题能力的影响[J].西南师范大学学报,2004(2):128-129.
聂岸义,湖南省邵阳市龙须塘小学,小学一级教师;唐理,湖南省邵阳市龙须塘小学,小学一级教师。
湖南省邵阳市龙须塘小学)

