基于干扰协方差矩阵重构的自适应波束形成

文/程院兵 郑昱

基于干扰协方差矩阵重构的自适应波束形成

文/程院兵 郑昱

针对传统基于采样协方差矩阵的自适应波束形成在样本数少、训练数据中存在期望信号等条件下，干扰抑制性能严重下降问题，提出一种基于干扰协方差矩阵重构的自适应波束形成算法。该算法采用自适应谱估计回波空间谱，从角度维将空间谱分为期望信号区域和干扰区域，通过对干扰信号区域积分重构干扰协方差矩阵。与传统方法相比，该算法可避免训练数据中包含期望信号，且利用自适应谱估计提高干扰空间谱的估计精度，从而提高干扰协方差矩阵估计精度。仿真结果证明了所提算法的有效性和优越性。

自适应空间谱估计 矩阵重构 自适应波束形成

自适应波束形成(ADBF)技术作为阵列信号处理领域的重要分支，被广泛应用于雷达、声呐、无线通信和语音处理等领域[1-8]，可根据接收阵列数据自适应计算波束形成权值，抑制干扰。总所周知，自适应波束形成对阵列模型和信号模型失配敏感，传统基于采样协方差矩阵(SCM)的自适应波束形成，在训练数据中存在期望信号情况下，会出现期望信号自消。随着信噪比(SNR)的增加，期望信号分量增加，尤其在高SNR下，输出信干噪比(SINR)损失严重[2-5,8]。

为改善ADBF稳健性，采用SCM的对角加载技术可缓解有用信号自消问题，但该方法对场景敏感，不同场景需要选择不同的对角加载因子[4]。文献[5]将空间角度离散化，采用对干扰角度搜索格点的CAPON空间功率谱求和得到干扰加噪声协方差(INCM)，避免INCM中包含期望信号，但对于非角度搜索格点的干扰，其空间谱估计误差大，造成INCM估计误差大。

本文从空域角度出发，提出一种自适应空间谱估计的干扰协方差矩阵重构算法。文章首先建立了回波信号模型，回顾了传统的基于采样协方差矩阵的自适应波束形成算法，然后给出了基于自适应迭代算法估计空间功率谱，通过对空间谱干扰区域积分重构干扰协方差矩阵，最后基于最小无失真方差响应(MVDR)实现干扰抑制。该算法避免了训练数据中包含期望信号，且利用自适应谱估计提高干扰空间谱的估计精度，从而提高干扰协方差矩阵估计精度。仿真实验表明，本文算法对非角度搜索格点干扰的协方差矩阵具有较好的估计精度，且在低SNR和高SNR下均可获得近似最优的SINR性能。

1 信号模型

假设接收天线阵列为等间距均匀线阵，阵元数为M，阵元间距为半波长。期望信号和干扰信号均位于远场，则回波信号可表示为

式中

对回波信号的波束形成输出为

式中w∈CMx1为波束形成权矢量，(·)H表示矢量或矩阵共轭转置。输出信干噪比(SINR)可表示为[8]

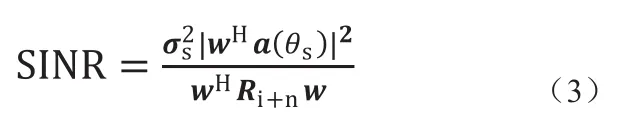
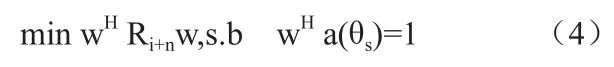
求解式（4），可得最优权值

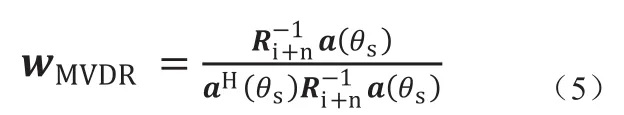
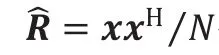
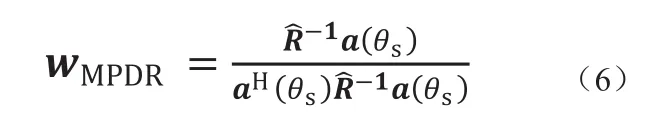
2 干扰协方差矩阵重构算法

2.1 基于自适应空间谱估计的干扰协方差矩阵重构

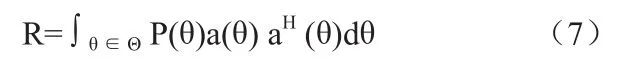
式中Θ=[-π/2,π/2]表示空间谱的角度区域。基于式（7），则干扰加噪声协方差矩阵可写为

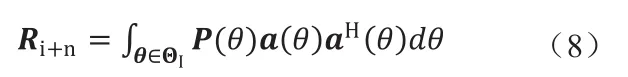
式中ΘI表示干扰角度区域。一般，干扰个数和方向未知，无法直接计算式（8），可采用下式计算

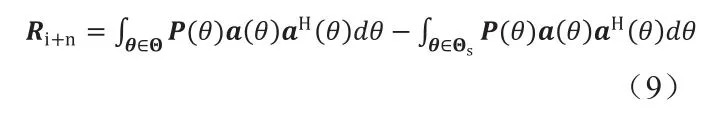
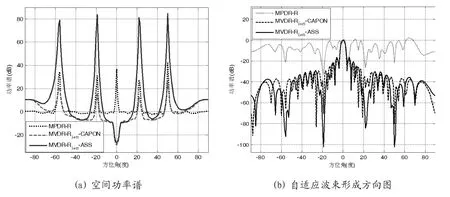
图1：空间功率谱和自适应波束形成方向图

式中ks1和ks2分别对应θs1和θs2对应的搜索格点索引。P(θk)表示第k个角度的空间功率谱。则基于Capon谱估计得到干扰加噪声协方差矩阵[5]

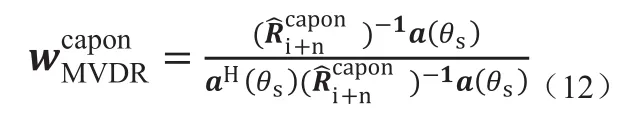
Capon谱估计能得到高分辨的空间谱，但当干扰角度不落在搜索格点上时，空间功率谱估计误差大，谱泄露严重。本文提出一种迭代自适应空间谱(ASS)估计算法估计干扰加噪声协方差矩阵。算法思路：计算第k个角度格点的空间谱时，其他角度格点的谱均认为是干扰项。第k个角度的干扰项协方差矩阵为

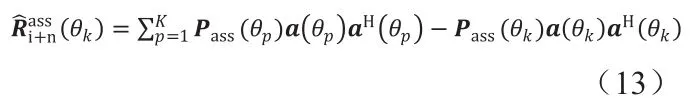
最小化除了第k点外的空间功率谱，需要求解代价函数

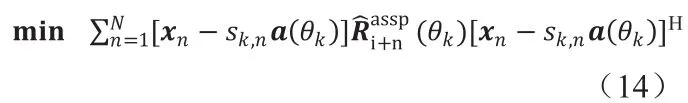
式中xn表示X的第n列,sk,n表示第n个采样点在第k个角度的信号。求解式(14)得

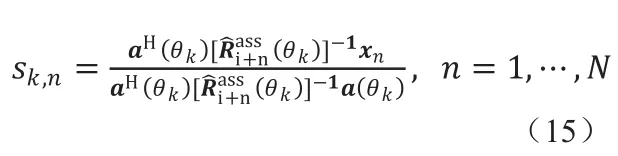
则第k个角度的自适应空间功率谱为

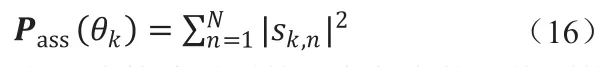
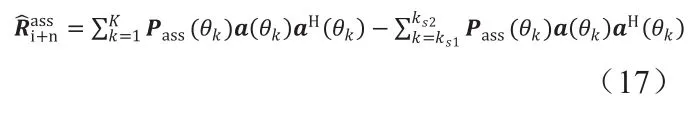
2.2 算法步骤

在2.1节基础上，总结本文基于自适应空间谱的干扰加噪声协方差矩阵重构算法步骤：

步骤1：初始化空间功率谱

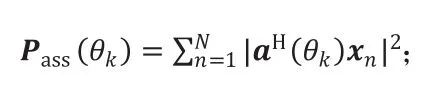
步骤2：迭代计算空间功率谱

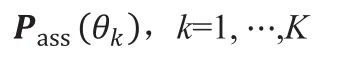
（1）将Pass(θk)带入式（13）计算协方差矩阵

（3）将sk,n带入式（17）计算Pass(θk)，k=1, …,K

（4）重复（1）～（3）至算法收敛，收敛准则可设置为相邻两次迭代Pass(θk)的相对误差小于某一极小值。

步骤3：将Pass(θk)带入式（17）计算干扰项协方差矩阵

步骤4：基于MVDR准则，本文基于干扰加噪声协方差矩阵重构的自适应波束形成权矢量

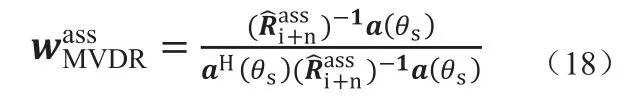
3 仿真结果与性能分析

假设雷达收发阵列的阵元数32，阵元间距半波长。发射信号为带宽5MB、脉宽20us、重复周期200us的线性调频(LFM)信号。目标信号角度0°，信噪比25dB，目标位于第180个距离门。下面从对干扰抑制性能和输出信干噪比与输入信噪比关系两个方面说明本文算法的有效性和优越性。仿真实验中，“MPDR-R”表示基于采样协方差矩阵和MPDR准则的结果，“MVDR-Ri+n-CAPON”表示采用Capon空间谱重构干扰加噪声协方差矩阵和MVDR准则的结果，“MVDR-Ri+n-ASS”表示采用本文提出的基于自适应空间谱重构干扰加噪声协方差矩阵和MVDR准则的结果，“DBF”表示未采用自适应算法的常规波束形成。

3.1 实验1：干扰抑制性能

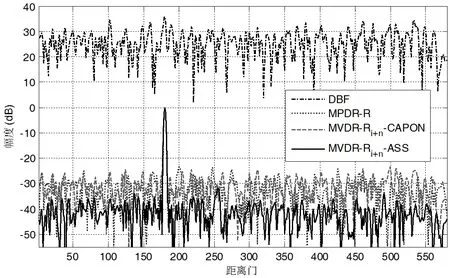
图2：干扰抑制输出结果

图2给出了DBF和上述三种方法的干扰抑制输出结果。可以看出，干扰抑制前，DBF输出目标SINR约6dB，无法检测。干扰抑制后，MVDR-Ri+n-ASS算法输出SINR=39.4dB，高于MPDR-R算 法7.7dB，高 于MVDR-Ri+n-CAPON算法11.5dB。这是因为MPDR-R算法中采样协方差矩阵中含有目标信号，造成信号自消；CAPON空间谱算法对干扰空间功率谱估计偏差大，造成干扰协方差矩阵估计误差大。

3.2 实验2：输出信干噪比与输入信干噪比关系

干扰参数、目标角度和距离门同实验1。图3给出了输出信干噪比与输入信干噪比关系。图中MVDR-Opt为基于式(5)最优权值得到的结果，MVDR-R为基于式(6)权值得到的结果，MVDR-Ri+n-CAPON为式(12)权值的结果，MVDR-Ri+n-ASS为基于式(18)权值的结果。可以看出，MVDR-Opt接近输出SINR理论值M×SNR，本文MVDR-ASS算法结果在低SNR和高SNR下的SINR均与最优权值结果接近，优于MPDR-R和MVDR-Ri+n-CAPON算法。这是因为：采样协方差中含有目标分量，造成MVDR-R方法随着输入SNR的增大，输出SINR损失严重；本文基于自适应空间谱(ASS)算法相比基于CAPON谱算法具有更高的干扰功率谱估计精度，可提高干扰协方差矩阵估计精度。

图3：输出SINR与输入SNR的关系

4 结束语

本文提出一种基于干扰协方差重构的自适应波束形成算法。该算法采用自适应迭代方法估计空间功率谱，通过对空间功率谱积分重构干扰协方差矩阵。与基于采样协方差矩阵算法相比，本文算法避免了由于协方差矩阵中包含目标信号引起的信号自消，且在低SNR和高SNR下均可获得近似最优的SINR性能。同时，本文算法对落在非角度搜索格点的干扰同样具有较高的功率谱估计精度，提高了干扰协方差矩阵估计精度，从而改善干扰抑制性能。

[1]H.Ruan and R.C.de lamare.Robust adaptive beamforming using a lowcomplexity sharinkage-base mismatch estimation algorithm[J].IEEESignal Processing Letter,2014,21(17)：60-64.

[2]Bin L.,Chongtao G.and Lei H.et al.Robust adaptive beamforming with random steering vector mismatch[J].Signal Processi ng,2016,129(04)：190-194.

[3]F.Shen,F.Chen and J.Song.Robust adaptive beamforming based on steering vector estimation and covariance matrix reconstruction[J]. IEEE Communications Letter,2015,19(09)：1636-1639.

[4]Li J.,Stoica P.and Wang Z. On robust Capon beamforming and diagonal loading[J].IEEE Transactions on Signal Processi ng,2003,51(07)：1702-1715.

[5]Y.Gu,N.A.Foodman,and S.Hong,et al.Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J].IEEE Transactions on Signal Processi ng,2012,60(07)：3881-3885.

[6]陈沛,赵拥军,刘成城.基于稀疏重构的共性阵列稳健自适应波束形成算法[J].电子与信息学报,2017,39(02)：301-308.CHENPei,ZHAOYongjun,LIUChengc heng. Robust adaptive beamforming algorithm for conformal arrays based on spares reconstruction[J].Journal ofElectronics and Information Technology,2017,39(02)：301-308.

[7]李立欣,白童童,张会生,等.改进的双约束稳健Capon波束形成算法[J]. 电子与信息学报,2016,38(08)：2014-2019.LI Lixin,BAITongtong, ZHANG Huisheng,et al.Improved double constraint robust Capon beamformingalgorithm[J].Journal of Electronics and Information Techn ology,2016,38(08)：2014-2019.

[8]Li J.andStoica P.Robust adaptive beamforming[M].New Jersey：John Wiley & Sons Press,2006.

[9]王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京：清华大学出版社,2004.WANG Yongliang,CHEN Hui,PENG Yingning, et al.Spatial spectrum estimation theory and algorithm[M]. Beijing： Tsinghua University Press,2004.

作者单位 南京电子技术研究所 江苏省南京市 210039

程院兵（1984-），男，江苏省南京市人。博士学位。现为南京电子技术研究所工程师。主要研究方向为机载雷达信号处理、MIMO雷达信号处理、谱估计等。