渐近非扩张型映象具有误差的迭代收敛性

林媛，张树义*，丛培根

（渤海大学数理学院，辽宁 锦州 121013）

渐近非扩张型映象具有误差的迭代收敛性

林媛，张树义*，丛培根

（渤海大学数理学院，辽宁 锦州 121013）

本文研究目的是在范数是一致Gateaux可微的Banach空间框架下,研究渐近非扩张型映象具有误差的迭代序列的收敛性,在没有任何有界条件下,使用新的分析技巧建立了具有误差的迭代序列的强收敛定理,最终从多方面推广和改进了有关文献中的结果。

一致Gateaux可微；渐近非扩张型映象；具有误差的迭代序列；不动点

非线性算子不动点理论作为非线泛函分析的重要组成部分,被广泛应用于微分方程、积分方程、优化理论、数学规划问题等许多领域,因此研究Banach空间中非线性算子迭代序列的收敛性无疑具有重要的理论意义。

Wittmann[1]证明了如果E是 Hilbert空间,T：D→D是一非扩张映象,如果满足条件 0≤αn≤1,则由下式定义｝强收敛到T在D中的某一不动点；Shimizu et al[2]把Wittmann的结果推广到范数是一致可微的Banach空间的情形；Cihdume et al.[3]在具有一致正规结构且其范数是一致Gateaux可微的Banach空间中,对任意给定的x0,u∈D,研究了迭代序列并证明了序列强收敛到渐近非扩张映象T：D→D的不动点；Chang et al[4]在具一致Gateaux可微范数的Banach空间中,引入和研究了由下式定义的迭代序列在一定条件下,证明了序列｛xn｝强收敛到渐近非扩张映象T的不动点；徐良才等[5]改进和推广了上述的结果，在具一致Gateaux可微范数的Banach空间的框架下,及在序列｛yn｝有界性的条件下,研究具误差的迭代序列｛xn｝强收敛到渐近非扩张映象的不动点问题。另一方面,许多学者研究了一些非线性映象不动点的迭代收敛问题[6-21]。

受上述工作启发,本文的目的是研究渐近非扩张型映象的具误差的迭代序列｛xn｝强收敛问题。在没有任何有界条件下,证明了新的强收敛定理,从而改进和推广了有关文献中的相应结果。

1 预备知识

2 主要结果

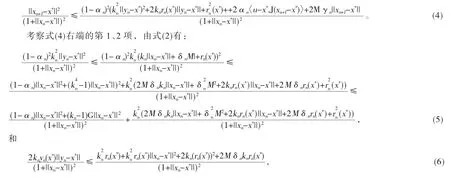
3 结语

渐近非扩张型映象是一类比较广泛的非线性映象类，它以非扩张映象和渐近非扩张映象为特例。随着非线性映象不动点理论的发展,提出并研究新的非线性映象类以及逼近这类非线性映象不动点的迭代算法,借以统一前人的一些结果,这应该是非线性映象迭代逼近理论的研究趋势之一。 本文我们研究了这类渐近非扩张型映象不动点的带有误差的迭代序列的收敛性,最终将相关文献中的结果,推广到了渐近非扩张型映象类,扩展了相关定理的适用范围。

致谢：作者衷心的感谢审稿专家对本文提出的修改意见。

[1]Wittmann R.，Approximation of fixed points of nonexpansive mapping[J].Arch Math，1992，58:486-491.

[2]Shioji N，Takahashi W.Strong convergence of approximated sequence for nonexpansive mappings[J].Proc Amer Math Soc，1997，125(12):3641-3645.

[3]Cihdume C E，Li J，Udomene A.Convergence of paths and approximation of fixed points of asymptotically nonexpansive mappings[J].Proc Amer Math Soc，2004，133(2):473-480.

[4]Chang S S，Le H W，Chan C K.On Reich strong convergence theorems for asymptotically nonexpansive mappings in Banach spaces[J].Nonlinaer Anal，2007，66(1):2364-2374.

[5]徐良才，张石生.Banach空间中渐近非扩张映象具有误差的迭代序列的收敛性[J].数学学报，2008，51(1):99-108.Xu Liangcai，Zhang Shisheng.Strong convergences theorem for asymptotically nonexpansive mapping with errors in Banach spaces[J].Acta Mathematica Sinica，2008，51(1):99-108.

[6]倪仁兴.一类广义Lipschitz非线性算子的带误差的Ishikawa迭代程序[J].数学学报，2001，44(4):701-712.Ni Renxing.Ishikawa Iteration procedures with errors for certain generalized Lipschitzian nonlinear operators[J].Acta Mathematica Sinica ，2001，44(4):701-712.

[7]谷峰.两个有限族一致Lipschitz映象的平行迭代算法的强收敛定理[J].数学学报，2010，53(6):1209-1216.Gu Feng.Strong convergence theorems of a parallel iterative algorithm for two finite families of uniformly Lipschitzian mapping[J].Acta Mathematica Sinica，2010，53(6):1209-1216.

[8]张树义.赋范线性空间中渐近拟伪压缩型映象不动点的修改的广义Ishikawa迭代逼近[J].应用数学学报，2011，34(5):886-894.Zhang S Y，Modified generalized Ishikawa iterative approximations of fixed point for asymptotically quasi pseudocontractive type mappings in normed linear spaces[J].Acta Math Appl Sinica，2011，34(5):886-894.

[9]张树义.一致Lipschitz渐近型拟伪压缩映象多步平行迭代算法的收敛性[J].系统科学与数学，2013，33(10):1233-1242.Zhang S Y，Convergence of multi-step parallel iterative algorithms for uniformly Lipschitz asymptotically type quasi pseudocontractive mappings[J].J of Systems Science and Math Sciences，2013，33(10):1233-1242.

[10]张树义，宋晓光.广义Lipschitz半压缩算子的迭代收敛性[J].北华大学学报(自然科学版)，2013，14(5):520-525.Zhang shuyi，Song xiaoguang，Iterative convergence of general Lipschitz hemi-contractive mappings，J.of Beihua Universities(Natural science)，Journal of Beihua Universities(Natural science)，2013，14(5):520-525.

[11]张树义，赵美娜，李丹.渐近半压缩映象具混合型误差的迭代收敛性[J].北华大学学报(自然科学版)，2015，16(3):165-169.Zhang shuyi，Zhao Meina，Li Dan，Convergence of iterative sequences for Lipschitzian asymptotically demicontractive mappings with mixed errors.Journal of Beihua Universities(Natural science)，2015，16(3):165-169.

[12]张树义，宋晓光.非Lipschitz有限族集值广义渐近半压缩映象的强收敛定理[J].系统科学与数学，2014，34(9):1051-1058.Zhang shuyi，Song xiaoguang.Strong convergence theorems of non-Lipschitz finite family setvalued generalized asymptotically hemicontractive mappings.Journal of Systems Science and Math.Sciences，2014，34(9):1051-1058.

[13]张树义，宋晓光.Hilbert空间中强伪压缩映象的一个注记[J].浙江师范大学学报(自然科学版)，2014，36(1):28-30.Zhang shuyi，Song xiaoguang，A note on iterative approximation of fixed points for strongly pseudocontractive mappings in Hilbert space[J].Journal of Zhejiang Normal Universities(Natural science)，2014，36(1):28-30.

[14]赵美娜，张树义，赵亚莉.有限族广义一致伪Lipschitz映象公共不动点的迭代收敛性[J].烟台大学学报(自然科学与工程版)，2017，30(1):7-10.Zhao Meina，Zhang Shuyi，Zhao Yali.Iterative convergence of common fixed points for a finite family of generalized uniformly quasi-Lipschitz mappings[J].Journal of Yantai Universities(Natural science)，2017，30(1):7-10.

[15]张树义，李丹，丛培根.增生算子零点的迭代逼近[J].北华大学学报(自然科学版)，2017，18(2):1-7 Zhang Shuyi，Li Dan，Cong Peigen，Iterative approximation of zero points for accretive operators[J].Journal of Beihua Universities(Natural science)，2017，18(2):1-7

[16]赵美娜，张树义，郑晓迪.一类算子方程迭代序列的稳定性[J].轻工学报，2016，31(6):100-108.Zhao Meina，Zhang Shuyi，Zheng Xiaodi.Stability of iterative sequences for a class of operators equation[J].Journal of Light Industry，2016，31(6):100-108.

[17]张树义，刘冬红，李丹.次增生算子方程的迭代解[J].北华大学学报(自然科学版)，2015，16(5):574-578 Zhang Shuyi，Liu Donghong，Li Dan，Iterative solutions for operators equation with Subaccretive[J].Journal of Beihua Universities(Natural science)，2015，16(5):574-578

[18]Zhang S Y，Song X G.Another note on a paper“Convergence theorem for the common solution for a finite family of strongly accretive operatior equations”[J].Appl Math Comput，2015，258(1):367-371.

[19]Mogbademu A A.A note on multi-step approximation schemes for the fixed points of finite family of asymptotically pseudocontractive mappings[J].Intern J Anal Appl，2013，1(2):106-112.

[20]Olisama V O，Mogbademu A A，Olaleru J O.Convergence of a modified multi-step iterative scheme for nearly uniformly Lipschitzian asymptotically pseudo-contractive mappings[J].Intern J Anal Appl，2014，4(2):192-200.

[21]Yao Y H，Postolache M，Kang S M.Strong convergence of approximated iterations for asymptotically pseudocontractive mappings[J].Fixed Point Theory and Applications,2014,100(1):1-13.

Iterative convergence with errors for asymptotically nonexpansive type mappings

Lin Yuan，Zhang Shuyi*，Cong Peigen
(College of Mathematics and Physics,Bohai University,Jinzhou,Liaonin 121013,China)

The purpose of this paper is to study convergence of iterative sequences with errors for asymptotically nonexpansive type mapping in Banach space with a uniformly Gateaux differentiable norm and establish strong convergence theorems of iterative sequences with errors for asymptotically nonexpansive type mapping without any bounded assumption by using a new analytical method.The results obtained in this paper extend and improve the corresponding results in some references from many aspects.

uniformly Gateaux differentiable;asymptotically nonexpansive type mapping;iterative sequences with errors;fixed point

O177.91

A

10.13880/j.cnki.65-1174/n.2017.04.020

1007-7383(2017)04-0513-05

2016-07-30

国家自然科学基金项目(11371070)

林媛（1991-）,女，硕士研究生，专业方向为非线性泛函分析。

*通信作者：张树义（1960-），男，教授，从事非线性泛函分析研究，e-mail:jzzhangshuyi@126.com。