地籍测量中光纤陀螺倾角测量技术及误差分析

郝春玲

(渤海船舶职业学院机电工程系，辽宁葫芦岛125100)

地籍测量中光纤陀螺倾角测量技术及误差分析

郝春玲*

(渤海船舶职业学院机电工程系，辽宁葫芦岛125100)

为了解决传统地籍测量技术中所具有的低效、耗时以及受外界环境影响较大的缺点，基于倾角全方位测量理念与光纤陀螺寻找真北方技术联合应用在地籍测量过程中，通过一系列的补偿方法，使得光纤陀螺对外界误差源影响的抵抗力增加，运用误差分析其在地籍测量中的适用度，陀螺在精度为0.05°/h以及倾角误差为1'的工况下，光纤陀螺的定位误差约为

26.51 ″。结果表明了光纤陀螺倾角地籍测量的精度可以达到测量精度要求，因此是可行的。

光纤陀螺;地籍测量精度;倾斜寻北;误差模型

近年来，我国土地用途变得极为广泛，而随着我国经济发展进程的不断加快，土地价值亦呈现出逐年上升的趋势，在实际地籍测量过程中普遍采用全球定位系统(GPS)对土地测量进行过程中，对待测量土地范围进行定点定向处理，对待测土地进行边界定位［1-3］。

在土地测量确定点位时，在测量环境较为复杂的时候，传统的测量定位方法并不能实现准确、稳定快速的布置土地边界测量分布点位图，此种方法欲想精确定位一个边界点，需要几个人对样本点位进行反复移动［4-6］，效率大大降低，基于传统的RTK测量界定土地边界时，任何一个建筑物均会对其测量精度造成较大的影响，并且被测土地范围内的电信信号亦会对其产生干扰，形成测量噪声，这些均会使得传统测量方法的测量时间大大增加，并且在传统测量技术中，需要的x、y轴进行找平，如果被测土地表面不平，亦会对测量精度造成较大的影响［7-9］。

综上，本文结合地籍测量的实际特点，基于光纤陀螺测量中的倾角理论来对土地边界进行测定，分析地籍测量系统中所存在的误差以及定位测量精度，以实现光纤陀螺测量技术对其进行全倾角状态下的精确测量。

1 技术设计

光纤陀螺利用Sagnac效应，只是各自所采用的位相或频率解调方式不同，或者对光纤陀螺的噪声补偿方法不同。当环行光路绕垂直于所在平面并通过环心的轴以角速度旋转时，则沿顺、逆时针方向传播的两波列光波在环路中传播一周产生的相位差为［10］:

式中，ΔΦR为两束光的相位差，c为光速，L为光纤长度，D为光纤环直径，λ为波长，ω为旋转角速度，A为光传播路径包围的面积的向量表达。

光纤陀螺的工作原理是基于萨格纳克(Sagnac)效应。萨纳克效应是相对惯性空间转动的闭环光路中所传播光的一种普遍的相关效应，即在同一闭合光路中从同一光源发出的两束特征相等的光，以相反的方向进行传播，最后汇合到同一探测点，如图1所示。

若绕垂直于闭合光路所在平面的轴线，相对惯性空间存在着转动角速度，则正、反方向传播的光束走过的光程不同，就产生光程差，其光程差与旋转的角速度成正比。因而只要知道了光程差及与之相应的相位差的信息，即可得到旋转角速度。

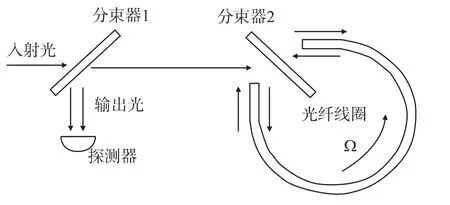
图1 光纤陀螺仪工作示意图

框架式陀螺仪由内框架和外框架组成，二者相互正交，均为挠性轴。检测质量固定在内框架上。检测质量绕驱动轴振动，由于振动角很小，故检测质量点的振动可认为是沿输出轴的线振动。当有角速度输入时，哥氏力作用在检测质量上，使其绕输出轴振动，测量电容差值的变化，得到正比于输入角速度的输出电压信号。其硬件构成和安装示意图如图2所示。

图2 硬件构成及安装示意图

本文在光纤环中人为地引入一非互易的补偿相移，以抵消由于光纤环旋转产生的Sagnac相移，补偿相移与Sagnac相移大小相等，方向相反。光纤陀螺始终工作在灵敏度最高的零位相差点附近，可以从补偿相移中获得陀螺的输出信号，这时陀螺的动态范围取决于引入补偿位相的器件性能。光纤陀螺避免了陀螺输出的非线性，动态范围广，检测精度高。并且能够自动调整优化状态，进行动态探测追踪。

1.1 光纤陀螺的寻北原理

光纤陀螺可以完全实现快速准确的进行寻北定位［11］，基于自动测量地球自转所产生的周期性角速度以及地球引力所产生的重力加速度的具体值，通过对光纤陀螺参考坐标轴测得的参考方向与实际北方所夹的角度进行自动解算，从而计算出测得的某一特定轴与真北方所夹的角度进而确定出待测土地边界的实际情况。

1.2 相关坐标系及其变换

将地球的三维坐标系变换为实测土地的三维坐标系，假设一实际坐标系OX0Y0Z0与实际地球坐标的初始点重合，在一系列的轴向运动以后的地球实际坐标系与本文假设坐标系一致，如图3所示。H、θ、γ为各坐标轴上的转动角度(欧拉角度)，此坐标转换的顺序可由余弦矩阵表示:

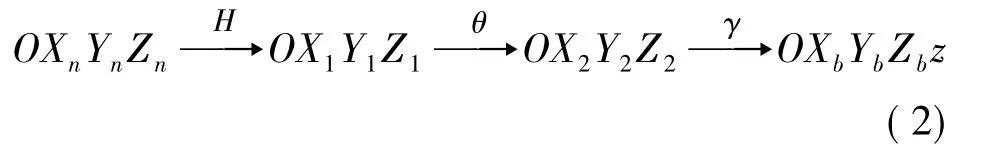
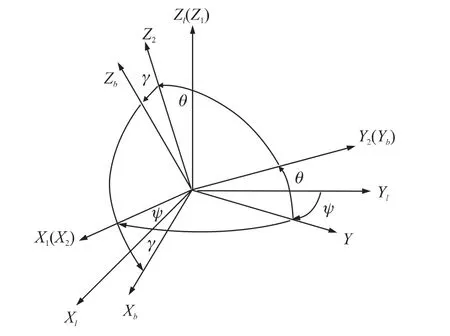
图3 坐标系变换示意图

OXlYlZl的各个坐标轴围着OZl转动的角度为H，完成第1步坐标变换，得到新的OX1Y1Z1坐标系，因此坐标变换表达式为:

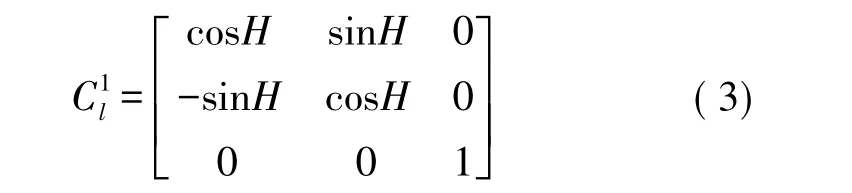
OX1Y1Z1的各个坐标轴围着OXl转动的角度为H，完成第1步坐标变换，得到新的OX2Y2Z2坐标系，因此坐标变换表达式为:

因此，OXlYlZl坐标系变换到载体坐标系OXbYbZb的变换表达式为:

OX2Y2Z2坐标系转换到载体坐标系OXbYbZb的变换表达式为:

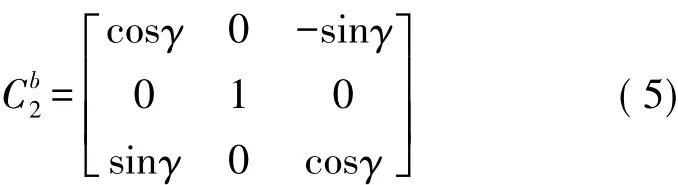
上式中基于矩阵运算的乘法法则为:

式中，H为运动方向角，θ为倾斜角，γ为横向运动角［12］。

然而，在实际的土地测量工作中，光纤陀螺在寻找真北方时进行解算时具有多种方法，但是解算过程中的基本理论是一致的。

在实际土地测量时，把光纤陀螺在三维坐标轴的转台上进行固定，在安装时应确保光纤陀螺的初始轴与载体坐标轴OYb重合，保持一致。光纤陀螺的采集信息敏感坐标轴与OYl之间的夹角角度为L，L为载体坐标系的偏北角［13］，如图4所示。亦或可说成光纤陀螺信息采集坐标轴与真北向之间所夹的角度。

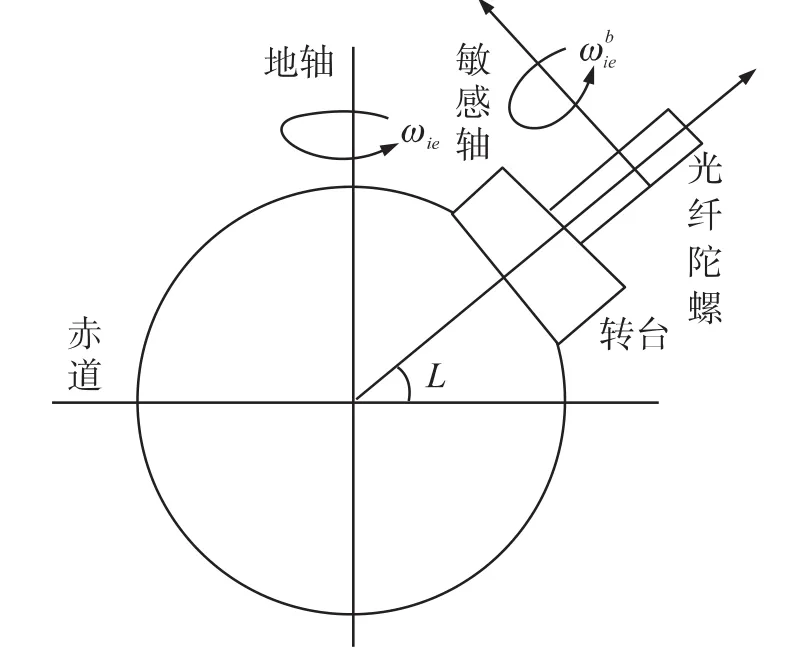
图4 寻北原理示意图

设定在地籍测量中的信息采集坐标轴在x-y坐标轴内，并且与载体坐标系中的y轴方向相同，其对于地球自转产生的角速度变化较为敏感，因此，在理想测量工况下光纤陀螺的输出表达式为:式中，ωie为地球自转的角速度，L为被测位置所处的纬度。

基于解算方法即可得到载体坐标系中的y轴方向与真北向所夹的角度，并且此种方法可直接确定出真北方，以此为基础即可实现自动确定方向。

1.3 倾斜寻北解算过程

测量地球重力加速度具体值的加速度计可以十分敏感的感应测量到重力加速度［14］，其在地球坐标系中存在的各方向的分量表达式为:

矩阵经过旋转变换得到的重力加速度在载体坐标系中的矢量分量的表达式为:

而安装光纤陀螺测量到的重力加速度在x向以及y向的分量表达式为:综上可得到:

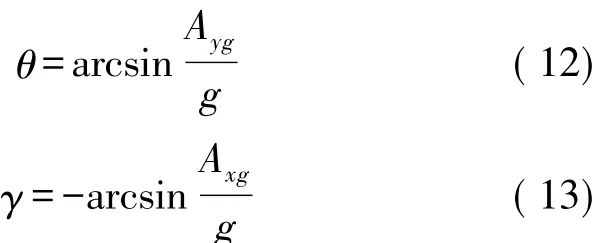
地球实际坐标系转换为实际被测载体的矩阵表达式为:

当安装光纤陀螺的固定台保持不动时，地球自转所产生的角速度在被测载体坐标系内部的投影表达式为:

式中，由于角θ，γ角度极小，因此sinγsinθ均为高阶无穷小量，即可忽略不计。由此可得光纤陀螺测得的载体角速度为:

光纤陀螺在寻真北过程中的输出表达式为:

式中，忽略光纤陀螺自身产生的漂移产生的误差，即可得到寻真北方的表达式:

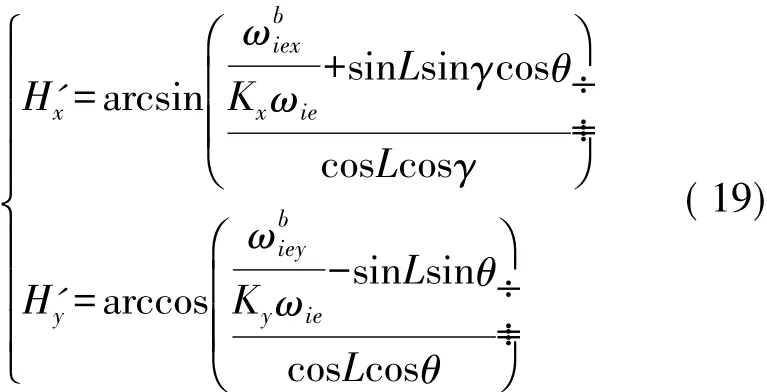
θ，γ均可忽略，即可得到:

因此:

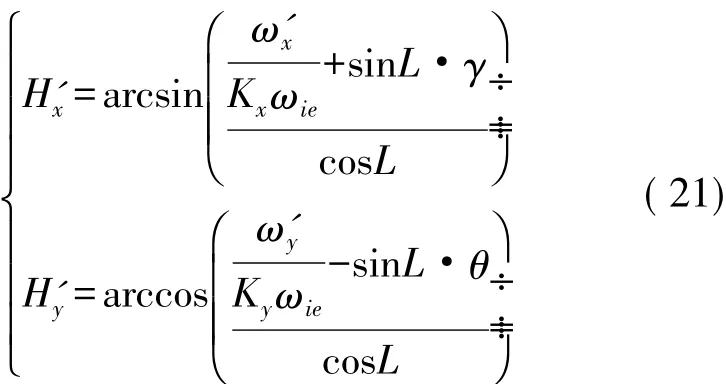
式中，H'x，H'y分别为解算出的寻真北所得的北方夹角。

2 系统误差分析

光纤陀螺寻北定位系统所产生的误差源主要由安装过程引起的误差、倾斜角度测量精度、陀螺产生漂移、转动以及其他不可预知的一系列外界干扰源。而安装误差作为上述误差源中的主要误差［15-16］。

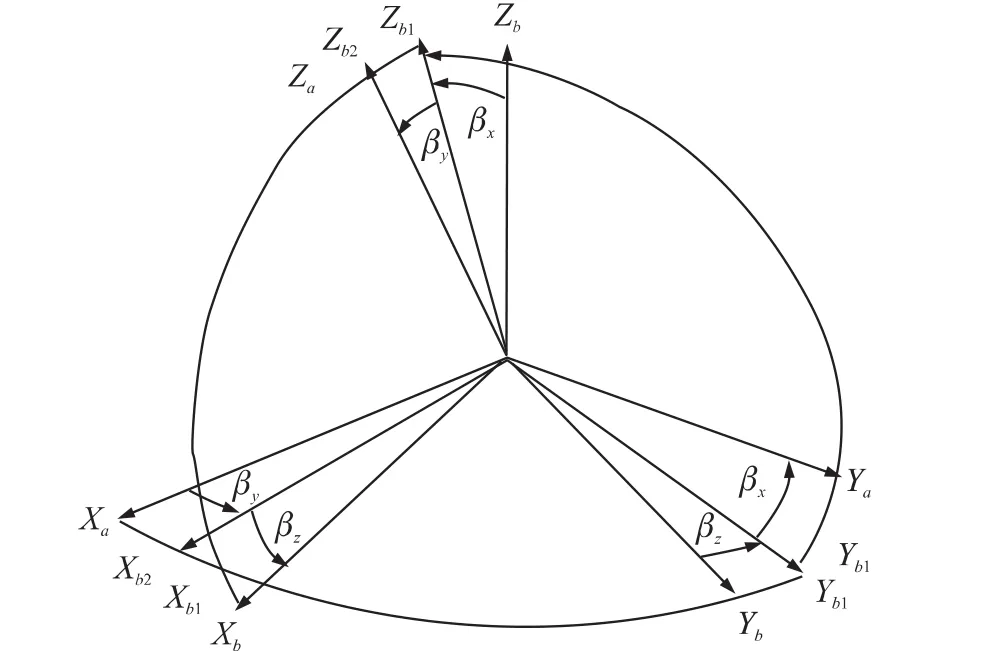
图5 光纤陀螺与全站仪主要轴系图

综上所述，光纤陀螺测量到的自转角速度在坐标系中的分量表达式为:

光纤陀螺在b坐标系转换到r坐标系中的表达矩阵为:

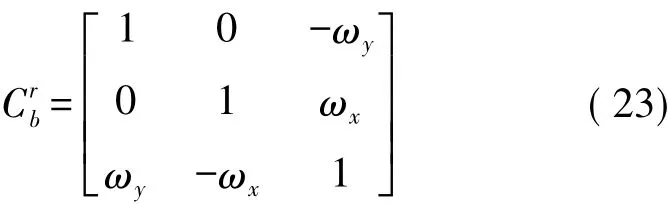
光纤陀螺固定台进行转动180°运行，受到转位误差的影响，固定台实际的转位角度为180°+ω2，舍掉二阶无穷小量以后基于三角展开公式可得:

综上，矢量角度转换公式为:

则有:

综上，即可求得光纤陀螺实际的安装以及转动误差，并且此误差等同于光纤陀螺的漂移，由下式可知其与ηz，ω2，ωy以及北向角H之间的关系较大。

由此可见，在实际测量中，补偿位置的适当增加，即可行之有效的避免光纤陀螺在安装时所产生的安装误差，此过程亦避免了再一次的对光纤陀螺进行标定，节约了光纤陀螺的工作时间。

图6为光纤陀螺在测量过程中产生的漂移现象对其测量精度以及定位精确度的影响示意图，此过程是基于上述的解算算法计算得到的。

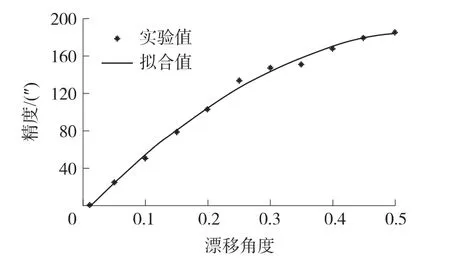
图6 陀螺漂移对定向精度的影响

忽略并去掉其他影响光纤陀螺的小误差源，假定光纤陀螺安装时所产生的漂移误差幅度为0.05 °/h，基于上述计算公式，可得到光纤陀螺在初始方向位置角度不同时，其定位精度的变化情况，见图7。

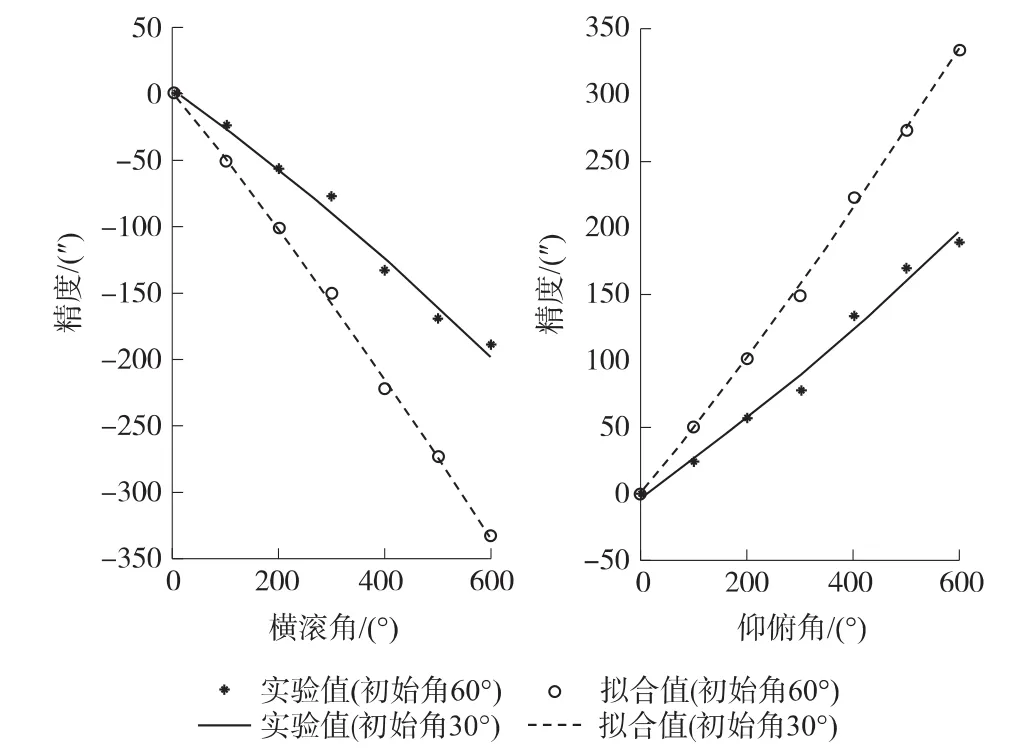
图7 倾斜角对定向精度的影响

图7表明光纤陀螺的定位精度随着其定位初始角的增加而大幅增加，亦表明了本文算法的精度较高，实验值与拟合值符合度较好，这也说明了本文的解算算法能够提高光纤陀螺的定位精度。

3 总结

基于目前地籍测量过程普遍采用全站仪进行，这种测量技术需要耗费大量的人力物力财力，big且其定位测量精度受外界环境影响较大，并且影响其测量定位精度的因素较多，本文将现有的光纤陀螺融入了倾角测量定位技术并且结合了真北方定位技术理念，此技术在地籍测量定位过程中的精度较高，亦可大大的提高地籍定位测量的工作效率，节约大量的人力，并且不需要对待测量定位的土地进行规整，结合误差理论对其进行误差分析，并找到影响光纤陀螺精度的主要误差源，并对其进行实验研究以及仿真测试研究，将二者结果进行对比分析结果表明地位测量传感器的精度对陀螺的地籍测量中的定位精度具有极大的影响，因此应首先选取精度较高的传感器，而初始点的选取亦尤为重要，随着初始角的增大，光纤陀螺的定位精度变小，因此，在采用此类定位测量技术进行地籍界定时，应选取最适合的高精度传感器以及最优化的初始位置。

［1］刘东坡.光纤陀螺快速高精度寻北技术与实验研究［D］.南京:南京航空航天大学，2007:21-24.

［2］张志君.基于光纤陀螺寻北定向技术研究［D］.中国科学院，2005:34-35.

［3］白云超，刘思伟，田育民，等.高精度寻北仪的现状及发展趋势［J］.测绘科学与工程，2008，28(4):52-56.

［4］刘毅然.基于光纤陀螺寻北系统的研究［D］.哈尔滨:哈尔滨工程大学.2007:12-13.

［5］石仕杰.光纤陀螺寻北技术研究［D］.国防科学技术大学，2004:17-22.

［6］张彤，崔一平.集成光学国际研究进展［J］.电子器件，2004，27 (1):197-198.

［7］张桂才.光纤陀螺原理与技术［M］.北京:国防工业出版社，2008:180-184.

［8］曹鲜花，吴美平，胡小萍.Matlab在光纤陀螺随机建模中的应用［J］.航天控制，2007，25(1):18-20.

［9］田双太，宋全军.葛运建.基于惯性测量单元的数字铁饼设计及数据处理算法研究［J］.传感技术学报，2010，23(10):1516-1517.

［10］孙楠翔.光纤陀螺捷联航姿系统去噪研究和设计［D］.哈尔滨:哈尔滨工业大学，2007:24-28.

［11］席晋.加速度计数据采集系统的研究设计［D］.哈尔滨:哈尔滨工程大学，2009:34-35.

［12］李春虹.扰动基座下激光陀螺寻北仪的数据处理研究［D］.国防科学技术大学，2006:14.

［13］Beni Prier.North-Finding Module(NFM)Navigation［J］.The Second International Symposium on Inertial Technology，1998:152-159.

［14］Budkin V L，Redkin S P.Gyro Compassing on a Movable Object by Means of Angular Rate Sensor on the Basis of DynamicallyTuned Gyro［J］.The Second International Symposium on Inertial Technology，1998:143-151.

［15］Merhav J.A Nongyroscopic Inertial Measurement Unit［J］.Journal of Guidance，1982，5(3):227-235.

［16］Watson W S.Improved North Seeking Gyro［C］//Proceeding of IEEE PLANS’9 Position［J］.Location and Navigation Symposium，1992:121-125.

［17］TD/T1001.2012地籍调查规程［S］.

郝春玲(1978-)，女，黑龙江人，汉族，大学本科，工程硕士，副教授，渤海船舶职业学院机电工程系，专业教师，研究方向为机械自动化，shenqiuv@163.com。

Cadastral New M ethod for M easuring Based on the Level Sensor_FOG_TS Combination

HAO Chunling*

(Bohai Shipbuilding Vocational College，Huludao Liaoning 125000，China)

In order to solve the problems of measurement techniques which has inefficient，time-consuming and observing environmental impact seriously defective.The technology of FOG north finding was combined with inclination measurement which will be used in cadastration.It gives steps of misalignment self-compensating of FOG;And it reduce errors in fiber optic gyroscopes(FOG)to improve its performance.FOG accuracy 0.05°/h in case，when the angle measurement error of 1'，the directional error is 26.51″.The results show the practice has proved that the FOGmeasurement’s precision can meet the request.

FOG;cadastral survey accuracy;slope north finding;errormodel

C:7630

10.3969/j.issn.1005－9490.2017.01.029

P24

:A

:1005－9490(2017)01－0152－06

2015-10-26修改日期:2016-07-29