爆破下质点峰值振速大小的多元回归分析

蔡清池，刘 春，姜 泽

（宁德师范学院 艺术系，福建 宁德 352100）

爆破下质点峰值振速大小的多元回归分析

蔡清池，刘 春，姜 泽

（宁德师范学院 艺术系，福建 宁德 352100）

基于萨道夫斯基经验公式，考虑质点振动频率的影响，提出质点振速的修正公式，并分别对萨道夫斯基公式和修正公式中的参数进行回归分析计算。分析结果表明：在进行质点振速的计算时，通过对振动频率、药量指数、场地系数、装药系数的多元线性拟合，能获得更合理的质点振动峰值速度计算值。

爆破振动；质点振速；振动频率；药量指数；回归分析

工程爆破在带来巨大经济效益的同时，爆破地震导致的振动效应问题日益突出。目前，世界上众多国家的爆破地震动安全标准几乎都采用爆破振动速度限值作为评价爆破振动效应大小的指标。虽然各个国家关于爆破振动的质点振速的计算方法各不相同，但质点振速大小主要与装药量、药量指数、质点与爆破中心的距离和场地地质条件相关[1]。随着工程实践的进行，人们发现质点振动频率对质点振动速度有着不可忽视的影响[2-4]。因此我国《爆破安全规程》引入了速度-频率的评价方法[5-6]。但是该评价方法只是定性地表达出频率对振动速度的影响，并未明确给出质点振动频率和速度大小之间的解析关系式。萨道夫斯基根据弹性动力学理论提出计算质点振速的经验公式，并提出了药量指数的概念。不过，该经验公式中药量指数的取值颇具争议。在公式参数拟合过程中，虽然药量指数一般取1/3，但是在许多情况下药量指数取1/2，拟合效果更好[7-8]。此外，萨道夫公式并未考虑到质点振动频率对振动速度大小的影响。

本文通过对比不同药量指数下萨道夫公式参数的回归分析结果，提出质点振速计算的修正公式，并进行回归分析评价其合理性，以归纳出露天深孔爆破下质点峰值振速的合理计算方法。

1 质点峰值振速的计算方法

爆破地震波的传播是一个复杂的动力学问题。影响振动速度大小的原因有很多，可归纳为与装药有关的影响因素和与工程地质条件相关的影响因素。实践表明，一般在采用2#岩石炸药条件下，药量大小及爆心距是影响质点振速的主要因素，并且在某个特定爆区，地形、地质条件及装药结构、堵塞条件较长时间内为一固定值[9]。

萨道夫斯基基于弹性动力学理论提出了计算质点峰值振速的经验公式，其具体形式为：

其中，v表示实测速度（cm/s），Q 表示微差爆破最大分段药量（kg），R 表示爆心距（m），ρ=Qβ/R 为比例药量，K为与介质有关的场地系数，α为衰减指数，β为药量指数。当β取1/3时，该公式为我国《爆破安全规程》推荐采用的计算公式。为了确定不同药量指数下该公式的待定系数值K，α，通过最小二乘法或偏最小二乘法原理对其进行一元线性回归分析或者多元线性回归分析。通过回归分析确定不同药量指数下的质点峰值振速计算公式中的参数，对实测振速和回归分析下的理论振速进行误差分析并进行F分布检验，选取最优的计算公式。

对公式（1）两边同时取对数得：

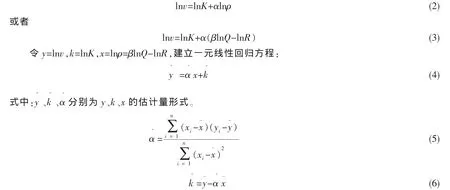
线性回归方程是否具有实用价值，通常是根据其回归精度和通过假设检验的方法来判断。在回归直线的估计精度问题上，定义观测点的预报值与均值的偏差平方和为回归平方和，观测点的预报值与实测值的偏差平方和为残差平方和。因此实际校正平方和为回归平方和与残差平方和的总和[10-12]。因此定义回归平方和与校正平方和的比值为判定系数，表达式如式（7）：

此外，根据实际观测到的数据，运用假设检验的方法可以判断其回归是否具有实用价值，即显著性水平判断[13]。首先对假设进行统计量检验，获取F统计量，再由给定的显著水平α（本文中显著水平α=0.05），查F分布表，得临界统计量Fα（p，n-p-1），其中p代表自由度，n代表统计数据个数。若F＞Fα（p，n-p-1），则认定回归方程显著，反之则认为方程不显著。对于多元线性回归模型，总体回归方程线性关系的显著性，并不意味着每个自变量对因变量的影响都是显著的，因此有必要对每个自变量进行显著性的检验。文章中关于多元线性回归模型中判定系数的修正（修正后判定系数用r¯2表示）和回归系数的显著性检验（t-检验）采用文献[13]的检验方法进行。

2 不同药量指数下的线性回归分析

2.1 工程概况

邢衡高速公路邢台段LJSG-2合同段位于邢台县会宁镇境内，在里程K8+880～K9+960约1080 m为山体石方需要爆破开挖。该区段经过区域为丘陵地带，海拔在100 m左右，地形复杂、河谷发育、沟室纵横、洼地较多，为以丘陵为主，丘陵平原相间，河流山脉走向自成体系的海岛丘陵地势。该地区属华北地层区，该地层区的特点是，早元古代变质岩系褶皱基底之上，不整合地覆盖着轻微变质的地台型海相沉积的中上元古代地层，而后沉积了稳定型的海相寒武第和奥陶系，中石炭世和二叠纪开始出现海陆交互相沉积，此后主要接受陆相地层的沉积。

2.2 回归分析

以邢衡高速公路邢台段LJSG-2路基开挖爆破为工程背景，该工程路基爆破采用露天深孔松动爆破。由于工程地质条件的部分差异和不同的速度监测传感器的测量精度不同，且不同的工程介质对爆破振动传播中能量衰减有不同的影响，使得实际监测的测量结果存在误差。因此为了保证分析比较的公平性和真实性,考虑到实际监测结果存在人为操作因素引起监测数据差异较大，在处理时剔除差异大的和不同地表介质条件下的监测数据，见表1，选取15组具有代表性的监测数据进行不同药量指数下的回归分析。

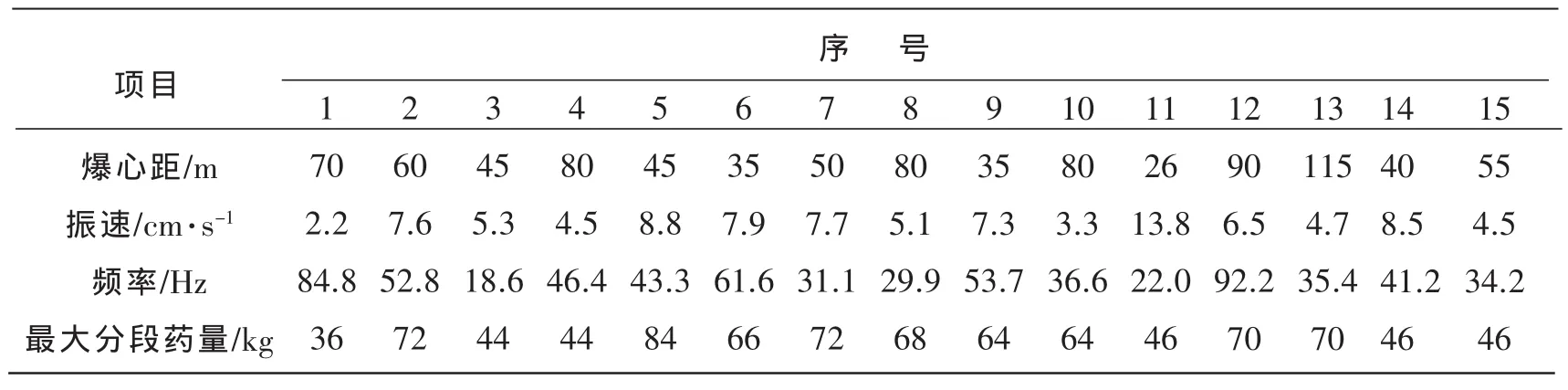
表1 邢衡高速公路工程路基爆破监测数据

通过对比国内外爆破振动质点峰值速度的计算方法发现，药量指数一般取1/2或1/3[8]。因此本文主要对此两种药量指数下质点峰值振动速度的计算公式进行参数的回归分析。结合公式（3）和公式（4），求得回归公式（4）中的回归参数值。计算结果见表2。

表2 不同药量指数下的对比分析

通过表2可见：F＞Fα（p，n-p-1），该回归方程显著。同时，经检验，该回归方程自变量对因变量影响显著。当β取1/2时，有相对较优的回归方程，但是在此回归方程下依然不能良好地反映出3个变量之间的线性关系，其修正后判定系数r¯2最大值仅为0.6306，可见大部分的数据仍偏离回归方程线。并且当β取1/2或1/3时回归分析所得的判定系数较为接近。这可能是因为路基爆破中，萨道夫斯基公式仅单独考虑了炸药量、爆心距、场地系数的影响，但是未考虑到爆破现场地形地貌情况，也未考虑质点振动速度大小与振动频率之间的关系。爆破是基于波的能量传递，首先引起周边质点产生振动频率而后产生质点振动速度的，因此，有必要对萨道夫斯基公式进行修正，使质点峰值振动速度与实际工程情况能较好的结合。

3 萨道夫斯基公式的修正与分析

在实际的工程实践中，许多人认为某一质点处的爆破振动速度与该质点的振动频率大小是密切相关的。此外，《爆破安全规程》中当药量指数取1/3时，萨道夫斯基公式在工程应用中往往未能取得良好的拟合效果。而当药量指量取1/2或者其他数值时，萨道夫斯基公式能更好地应用于工程上。由此，提出考虑频率影响下的修正公式：

式中：f表示质点振动频率，c表示频率指数。

为了便于公式的回归分析，公式（8）改写为：

式中：a=βα，b=-α。

依据之前的二元线性回归方法，对公式（9）两边同时取对数得：

令 y=lnv，k=lnK，x1=lnQ，x2=lnR，x3=lnf，建立的三元一次回归方程为：

根据表1的数据，对回归参数进行回归分析，回归方程公式（11）中，自由度p=3，可得：，经修正后判定系数¯2=0.6999，相比表 2中的计算结果有所提高，且F=8.5525，大于临界统计量Fα(3,11)=7.6，回归方程显著。运用文献[13]的检验方法，对回归方程进行t检验，结果满足要求，残差分析图见图1。其拟合方程为：

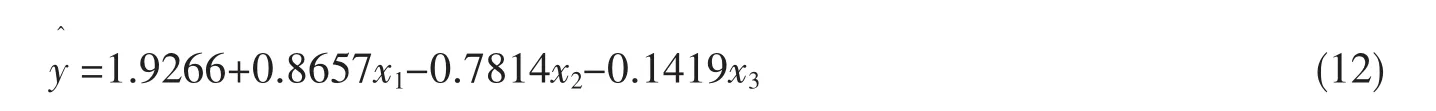
根据拟合方程参数计算得场地系数K=6.8661，药量指数β=0.8985，衰减指数α=0.7814，频率指数c=-0.1419，因此在本工程背景下，质点峰值振动速度公式为：

公式（13）的回归相关系数较之前有所提高，回归结果相对良好，在一定程度上反映了在路基地质条件下，爆破振动质点峰值振速随着比例药量减少而降低的规律,见图1。在公式计算中，由于测点与爆心基本位于同一高程，因此并未考虑高差对公式计算与拟合的影响。

可见，在露天深孔松动爆破下，萨道夫斯基公式的应用具有一定的局限性，并不能很好地预测现场的实际位置的质点振动情况，而通过对振动频率、药量指数与场地系数、装药系数的多元 线性拟合，能较好地获取贴近实际的质点振动峰值速度计算方法。建议在露天爆破作业下，特别是针对高速公路路基爆破中，在计算质点振动峰值速度时，应考虑质点振动频率的影响。

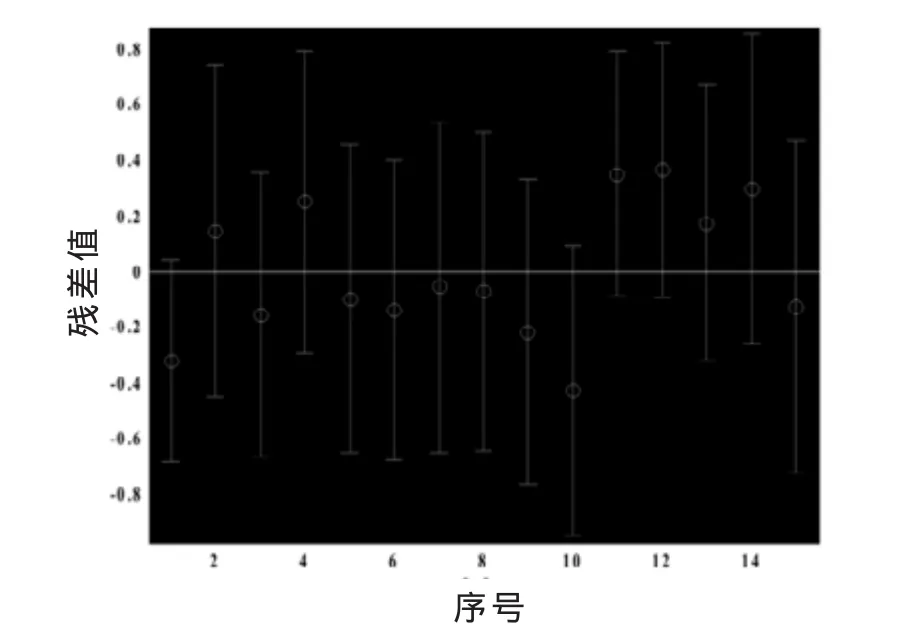
图1 残差值分布图

4 结论

（1）通过对邢台段LJSG-2路基开挖爆破振动实测数据进行不同药量指数下的一元线性回归，以及建立起二元线性回归方程求最优的药量指数，从而提高了回归分析下的判定系数，优化了回归结果，一定程度上反映了爆破振动质点峰值振速随着比例药量减少而降低的衰减规律。

（2）引入了质点振动频率参数，考虑了质点振动频率对爆破振动下质点峰值振速的影响，指出了在露天深孔爆破作用下萨道夫斯基公式的缺点。提出的萨道夫斯基公式修正方法，为工程实际中求取爆破振动下质点峰值振速大小提供借鉴，在爆破振动控制或类似工程中有重要的参考价值。

（3）在一元回归模型的基础上扩展到多元，通过多元回归线性方程给出了邢衡高速公路露天深孔爆破下质点峰值振速计算公式：

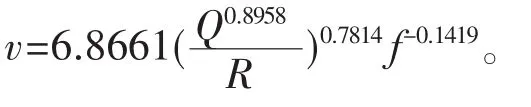
［1］张志毅，杨年华，卢文波，等．中国爆破振动控制技术的新进展［C］／／中国力学学会工程爆破专业委员会2013年年会，2013：25－32．

［2］ 韩博，马芹永．煤矿岩巷毫秒延期爆破振动测试与控制技术研究［J］．煤炭学报，2013，38（2）：209－214．

［3］ 吴亮，李凤，卢文波，等．爆破扰动下邻近层状围岩隧道的稳定性与振速阈值［J］．爆炸与冲击，2017，37（2）：208－214．

［4］ 何理，钟冬望，陈晨，等．岩质高边坡开挖施工的爆破振动监测与分析［J］．金属矿山，2017（1）：6－10．

［5］ 罗忆，卢文波，陈明，等．爆破振动安全判据研究综述［J］．爆破， 2010，27（1）：14－22．

［6］ 汪旭光．爆破手册［M］．北京：冶金工业出版社，2010：935－942．

［7］ 李顺波，杨仁树，杨军．精确延时爆破振动速度峰值预测模型［J］．工程爆破，2016，22（3）：79－82．

［8］胡英国，吴新霞，赵根，等．水工岩石高边坡爆破振动安全控制标准的确定研究［J］．岩石力学与工程学报，2016，35（11）：2208－2216．

［9］ 卢文波，张乐，周俊汝，等．爆破振动频率衰减机制和衰减规律的理论分析［J］．爆破，2013，30（2）：1－6．

［10］王信峰．概率论与数理统计［M］．北京：清华大学出版社，2016．

［11］任露泉．回归设计及其优化［M］．北京：科学出版社，2009．

［12］白杨，段卫东，徐园园，等．爆破振动高程放大效应的试验研究［J］．武汉科技大学学报（自然科学版），2015，38（3）：216－219．

［13］孙毅，刘仁云，王松，等．基于多元线性回归模型的考试成绩评价与预测［J］．吉林大学学报（信息科学版），2013，31（4）：404－408．

（责任编辑：朱联九）

The Multivariate Regression Analysis on Peak Velocity of Particle under Blasting

CAI Qing-chi,LIU Chun，JIANG Ze
（Department of Art,Ningde Normal University,Ningde 352100,China）

Based on the formula of Saudorsky,the correction formula of particle velocity is put forward after considering the influence of particle vibration frequency.Then the parameters in the formula of Saudorsky and the correction formula are analyzed and calculated in this paper.The results show that the more reasonable peak velocity of particle can be calculated when considering the influences of vibration frequency,quantity index,site coefficient,dynamite coefficient.

blasting vibration;particle velocity;vibration frequency;quantity index;regression analysis

TD235.1

A

1673-4343（2017）04-0083-05

10．14098 ／j．cn35－1288 ／z．2017．04．014

2017-04-18

宁德市科技局科研项目（20150180）

蔡清池，男，福建石狮人，助教。主要研究方向：岩土工程、边坡稳定性评价。