谐波源的神经网络系统辨识与样本建模

郭宝英，郑思凡

（1.仰恩大学 工程技术学院，福建 泉州362000；

2.黎明职业大学 机电工程与自动化学院，福建 泉州362000）

谐波源的神经网络系统辨识与样本建模

郭宝英1，郑思凡2

（1.仰恩大学 工程技术学院，福建 泉州362000；

2.黎明职业大学 机电工程与自动化学院，福建 泉州362000）

针对当前电网谐波的诊断与分类识别均依赖于大量的样本采集作特征提取，采用系统辨识的方法以三相直流励磁同步发电机为对象,以三相直流励磁电压和定子感应电动势为激励，对发电机的正常发电过程及暂态震荡与短路故障进行系统辨识。文中根据问题的实际情况确定了神经网络的类型结构，训练算法等参数，并给出了仿真实现。仿真结果表明，所训练的BP神经网络具有一定泛化能力并可用于激励参数异常的故障样本建模。

系统辨识；levenberg-marquardt；同步励磁发电机；VC维；BP神经网络

当前随着IGBT,GTO,大功率场效应管等电力电子器件在逆变，变流及开关电源驱动电路中大量推广应用[1]，电网中非线性负载诸如变频器、同步励磁电机、电压适配器，整流器、高频开关电源等比重越来越多，基于这些功率器件的开关电源技术虽然有着节约能源，提高效率和易于数字化，智能化的优点，但同时,也因为其非线性产生了大量的谐波注入电网中,使用电效率降低，供电质量变坏,对电气设备的寿命及故障产生不良影响。另一方面，以卷积神经网络为基础的深度机器学习算法因为具有能够自学习出代表信号特征的卷积核矩阵从而比传统的神经网络需要人为的去设计和选取特征矢量具有更优的性能及更少的偶然性而得到重视与发展，但是将深度机器学习用在谐波源与异常电网波形分类识别目前还处在发展的初期阶段，主要的问题在于深度学习因为其要提取的特征卷积核数目众多，隐层层数大，需要的训练样本比传统的神经网络更多，甚至跨越几个数量级。

正因为需要谐波样本数量繁多，其幅度与持续时间，功率谱分布及RMS等统计值呈现随机状态，在实际研究中不易实地采集，因此本文从三相直流励磁同步发电机的暂态震荡故障及断路故障波形为目标，采用系统辨识的方法，利用改进的动量误差反传作为训练学习算法，训练出一个多层BP神经网络对三相直流励磁同步发电机的故障波形进行拟合，并作为谐波源参与后续的数据处理分析，实验数据表明，该模型能够很好拟合以电路模型仿真的故障波形，在三相电压幅值改变情况下具有很好跟踪新的故障波形的能力，从而验证了模型验证模型对新故障样本的泛化能力。

1 谐波源系统辨识整体思路及架构

系统辨识可以具体定义为给定一个模型类[5]μ={M}（在本文中M为带权值矩阵参数的BP神经网络），一类输入信号u和等价准则J=L(y，yM)(其中J为误差函数，是过程输出y和模型输出yM的相减的泛函)；然后选择使误差函数J达到最小的模型来作为辨识所要求的结果。传统的辨识方法为根据系统满足的数学关系式将此泛函具体化为依赖于参数θ的方程组模型，而后对θ进行参数估计，这类算法一般应用于线性系统或经过局部微分近似处理后的可线性化的系统辨识，因为非线性的系统不能转换为参数空间矩阵自身与其转置的这种最小二乘格式，因而此类算法并不适用非线性系统，另一方面，神经网络对系统的辨识则是通过系统的输入/输出数据对自身的权值矩阵元素进行调整学习，使得每对的输入数据与给定的输出误差函数达到最小，因而不依赖理想的线性化的动力学等物理模型，所以对于非线性的系统的辨识具有更好的适应性。

图1给出了基于输出误差的神经网络辨识原理图。图中TDL(Tapped Delay Line)为多分头时延系统，其输出矢量由输入信号的延时构成。本文就以神经网络拓扑结构的选择、神经网络的权值矩阵的训练和网络泛化能力的检验这3个环节介绍同步励磁发电机两个故障谐波源的辨识过程。

图1 神经网络辨识原理图

2 系统模型结构与描述方法的确定

本文考虑的多相直流励磁发电机构造如图2，图中，转子由直流电源F提供励磁，定子的交流感应电动势A，B，C经过6个硅二极管全桥整流给负载供电，考虑到故障励磁发电的系统状态无法获得，及状态不都可测，本文将直流励磁电压u（k）、三相定子感应电动势作为系统辨识输入，输出为整流负载电压y（k），则当将此发电机及故障模型视为非线性动态系统时，其输入输出关系可采用非线性自回归滑动平均(NARMA)模型图3来描述[2-4]，在不考虑干扰及系统误差情况下系统可表示为：

其中[u（k），yp（k）]为 SISO（m≤n）系统在 k时刻的输入输出对，g为非线性函数，这样时刻 k+1上系统的输出由过去的n个输出值，m个输入值决定。因此g可用多层前馈神经网络建模。yp（k)作目标输出，整个模型关系式可用BP算法进行训练，确定g的权值元素。

图2 多相同步励磁交流发电机

图3 NARMA模型

本文要辨识的故障谐波源和正常发电过程是在负载上采样输出电压，系统的输入为励磁直流电压及定子感应电势，系统本身因为具有电容与电感等延迟元器件，所以一并考虑系统的历史输出。对于直流无刷励磁发电机来说,励磁绕组存在自感,转子绕组有三相,各有自感和互感,负载有一自感,故系统的阶次n取5,m取0。

3 神经网络结构参数的确定

3.1 网络VC维度及层数与各层节点数的设定

根据式(1)选择的NARMA模型，系统的阶次n取5，加上励磁输入与电枢电动势输入，故在此确定输入神经元个数为9，输出的目标样本是负载电压，故输出层取一个神经元，由映射存在定理[5]可知:“给定任一连续函数 f∶un→rm，f（x）=y。 这里 u 是闭单位区间[0，1]。 则 f总可以精确地用一个三层感知器网络实现”。因此本文在此取1层隐层。对于隐层节点数，本文参考BP神经网络的VC维度，保证样本数量足够情况下最优目标函数有解，具体公式如式（2）[9]：

其中m、n分别为输入结点数目与输出结点数目，将m、n值代入，可得本方案隐层取11个节点。

3.2 传输函数的选择

虽然BP网络刚开始时可以用于二值化的逻辑回归，但在处理模拟数据拟合和回归时为了方便计算误差的梯度，要求输出神经元的激活函数以及隐层神经元传输函数必须是连续可微的，通常选择S形函数，因采用logsig（x）函数，可能使网络陷入一个较大的平坦区导致收敛变慢。故在此选择tansig（x）函数为神经元的作用函数。

3.3 机器学习算法的选择及实现

鉴于传统的BP算法具有局部收敛的局限性，一旦梯度过小，程序将提前退出，为此我们考虑包含取函数二阶赫森矩阵的牛顿法的改进方案。即若将目标函数F（x）在等0处一阶泰勒展开并令其导数为零[7]，可得：

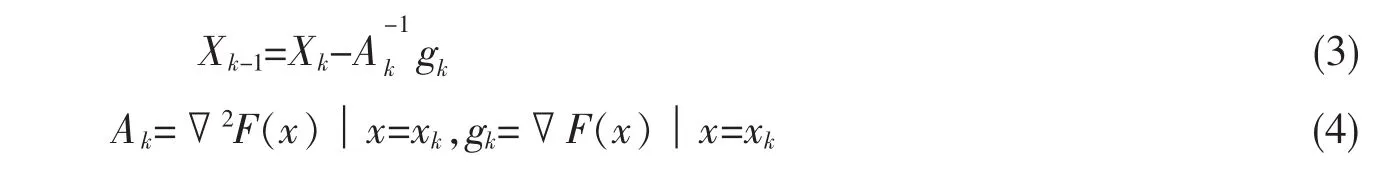
假设F（x）是平方函数之和，即

那么第j个梯度分量为：

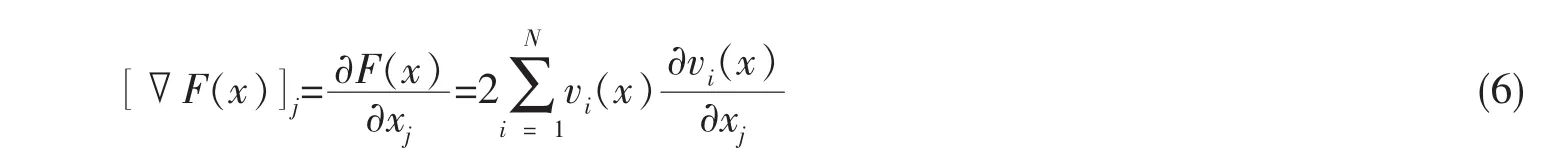
因此梯度可以写成矩阵形式：

赫森矩阵可以表示为：

将(10)式和(7)式代入(3)式，可以得到高斯-牛顿方法：

此算法的优点是不需计算二阶导数。由于矩阵H=JTJ可能不可逆，故用下述近似赫森矩阵代替:

由此可导出L-M算法：

对应地，在Matlab构造网络时只要传递“trainlm”参数即可。

3.4 数据归一化及采样间隔

因为隐层激活函数在 [0,1]之外函数趋于饱和，导致梯度变小，收敛速度慢，故必须对输入变量进行归一化。保证位于[0,1]之内，为简单起见，本文采用公式 :

来归一化，网络仿真结束之后，需要通过反归一化将仿真结果转换成原始数据尺度，也就是将仿真后的结果代入xl，得出sl，考虑到谐波分析的最高阶数25次，即1.25 K，采样间隔取0.00002 s，是最高分析频率的40倍，已满足奈奎斯特定理要求。

4 系统辨识激励设计及matlab实现

综上所述，本文对5阶NARMA辨识系统的神经网络的输入为发电机负载电阻电压的前5个采样值以及当前3个转子正弦交流激励电压瞬时值以及励磁电压值。此9个元素组成输入层各神经元的输入向量，具体为：[y（k-1），y（k-2），y（k-3），y（k-4），y（k-5），u（k），ε1（k），ε2（k），ε3（k）],其中y（k-1）由 y（k）右移形成,同理推广至 y（k-5）,为考虑神经网络本身的延迟效应,对 u（k）亦进行右移一单位,这样右移后,将靠前的数移至后面以决定后面的值,符合因果系统的要求。

根据参考文献[6]提供的仿真模型，在直流励磁电压不变情况下，对定子电动势以步长20取0～600 V的30组样本进行训练，另外令图2中节点X,节点Y电压为0，经过模型磁链回路方程及元器件U-I方程联立计算，可以得到断路故障负载波形数据作为辨识数据源样本，最后在电枢电压叠加因机械冲击或碰撞等的波形来得到暂态震荡故障波形样本。

综合上述,在matlab可用如下代码完成神经网络的初始化[8]:

net=newff([0 600;0 600;0 600;0 600;0 600;0 50;0 400;

0 400;0 400],[9,11,1],{'tansig','tansig','purelin'},'trainlm');

其中输入矩阵前五行为负载输出的过去历史输出形成的自递归矢量即 ,第六行为当前直流励磁输入。输出是一个神经元,为下一时刻的负载输出电压YT。

net=init(net);%以matlab默认的方式初始化

………….

YT=sordata';其中sordata为上述各需要辨识波形的数据源；

YT1=(circshift(sordata,1))';circshift为循环右移函数,YT1,YT2前被移元素必须补零;

YT2=(circshift(sordata,2))';

…………….

另外因为训练样本是取不同激励电压构成,故每次的输出矢量必须连接,这可以用cat函数完成

ZYT1=cat(2,ZYT1,YT1);ZYT2=cat(2,ZYT2,YT2);其中ZYT是累积连接的矢量样本。这样就把各种电压幅值参数的样本组合为较大的列向量，一次参与训练学习，最终的组合的输入矢量如下：Z=[ZYT1,ZYT2,ZYT3,ZYT4,ZYT5,E1,E2,E3,ZINPU];其中ZINPU为u（k）右移一位补零得到。

net.trainParam.show=10;%确定显示步数间隔

net.trainParam.epochs=400;%确定总训练步数

net.trainParam.goal=0.005;%目标性能误差

net.trainParam.lr=0.01;%学习率

net.trainParam.min_grad=14;%最小梯度值,小于此梯度退出。

[pn,meanp,stdp,tn,meant,stdt]=prestd(Z,ZYT);

其中 meanp,stdp,meant,stdt分别为输入和目标数据规范化后的均值和标准差,pn,tn分别为规范化后结果,他们才参与训练和模型验证即

[net,tr]=train(net,pn,tn);antemp=sim(net,pn);

验证结果antemp必须进行反归一化才可以与原信号相比较。即

yafter=poststd(antemp,meant,stdt);

5 训练仿真结果总结

对于正常励磁发电机电枢幅值从0～420 V的0.1 s发电过程辨识在训练过程中目标性能误差的下降情况如图4。

由图可见，30组样本经过50(图4步数间隔为10)轮迭代便达到误差目标0.005.收敛速度比较理想，各样本理想电路模型输出与辨识神经网络输出结果比对如图5。

图中虚线为训练前神经网络的输出，默认为零，训练后，则很好地拟合了各组发电过程中的全波整流后的周期起伏波形。将辨识输出与样本输出相减取绝对值可得辨识输出与系统输出的拟合误差如图6。

可以发现，辨识的输出与样本输出的误差在0.06%以下。 神经网络样本的输出与期望输出的均方差为err=0.0229,在Matlab命令窗口里可方便得到训练好的网络权值与偏置,其中隐含层的权w1和阈值b1为:net.IW{1,1}=

同理访问元胞数组net.LW{2,1},net.LW{2,3},net.b{2,1},net.b{3,1}可以得到隐层,输出层的权w2和阈值b2。

图4 0.1s发电过程辨识在训练过程

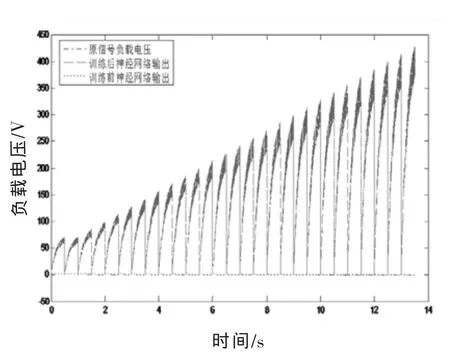
图5 系统输出与辨识神经网络输出结果比对

图6 辨识输出与系统输出的拟和误差

图7 暂态震荡故障辨识训练过程

同样可以得到暂态震荡故障的训练结果如图7。

从图可以看出，因暂态震荡在每个交变周期存在随机幅度与频率变化，波形突变较多，平滑度下降，网络需经过接近400次同组样本迭代才收敛，收敛速度比正常发电过程的拟合慢。暂态震荡的系统辨识拟合结果如图8。

图中可看出，拟合误差主要集中在波形尖峰突变点处，总体上数据MSE误差仍然可以达到要求。最后，关于断路故障的仿真与辨识训练过程及仿真结果对比如图9～10。

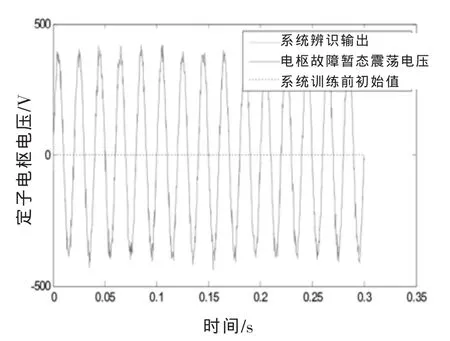
图8 暂态辨识输出与系统输出的比对

图9 断路故障的辨识训练过程

由图10断路故障的波形可以看出，断路故障含有较多的高次谐波分量，突变点较多，曲线平滑度严重下降致使训练过程在迭代350次后，误差梯度即趋于饱和，最终误差在0.05左右，从最终拟合的结果图（5～7）可以看出，误差集中在具有高次谐波的突变点处，理论上虽然可以通过增加隐层结点数来逼近更多的峰值点，但也会造成过拟合而降低泛化能力，因此只能在不影响实际应用的情况下降低误差要求。

图10 断路故障的系统辨识和系统仿真比对结果

6 泛化能力验证

现给系统输入50 V的交流定子激励以与样本20 V倍数幅值分开,时间0.1 s,采样间隔扩大为0.005来进行泛化能力检查，同样在函数调用前对输入数据归一化,仿真结束之后，需要反归一化将结果转换成原始数据尺度，实现代码如下:[pn,meanp,stdp,tn,meant,stdt]=prestd(Z,ZYT);meanp,stdp,meant,stdt分别为输入和目标数据规范化后的均值和标准差,pn,tn分别为规范化后结果,他们才参与训练和模型验证即[net,tr]=train(net,pn,tn);antemp=sim(net,pn);验证结果 antemp必须进行反归一化才可以与原信号相比较。即yafter=poststd(antemp,meant,stdt);得到的神经网络辨识模型的输出与系统的电路仿真输出比较结果如图11。

图11 三相直流励磁发电机的神经网络模型输出与系统的电路仿真输出

由此可见，系统在幅值与采样频率不同的条件下，BP神经网络辨识输出还是很好与电路模型仿真输出一致。

7 结论及展望

以常见的三相同步励磁发电机的正常发电与暂态震荡故障与断路故障为系统辨识目标，利用非线性NMARMA的前向递归模型作为反馈调整环节的辨识方法，对三种波形以不同的激励电压幅度为样本进行学习训练，实验仿真结果表明，本文的系统辨识方法能够很好地与参考文献6中依据发电机磁链等微分方程等数学模型以及利用Matlab内建的sim Power System模块库建立的发电机输出保持很高的一致性，误差在10-2数量级左右。同时修改转子输出交流电压幅度完成训练后，可以看到本系统也能很好的跟踪拟合训练之外的电压幅度，从而证明神经网络采用系统辨识的方法可以很好的泛化能力。

考虑到不管是Matlab的模块，还是利用磁链的微分方程建立的发电机模型都是在一些元器件理想化的模型进行抽象，使得模型存在系统误差，本文提出的利用神经网络则在非线性映射能力方面则更具有能够拟合实际场景中故障的波形的潜力，从而使得采用系统辨识构建谐波源样本对于进一步的深度学习与模式识别方面的研究方面具有广阔的前景。

［1］ 路德亮．简述电力谐波的产生、危害及治理方案［J］．中国科技博览，2012（18）：64．

［2］ 许慧雅，王华东．发电机励磁系统参数辨识的仿真研究［J］．计算机仿真，2013，30（6）；129－132.

［3］罗玉春．发电机励磁系统参数辨识研究［D］．南京：南京理工大学，2008.

［4］ 罗国云，严东超，祝雪平．基于 MATLAB 的同步发电机励磁系统仿真［J］．电气传动，2003（5）；62－64.

［5］陆桂琴．基于动态神经网络的非线性动态系统辨识［D］．银川：宁夏大学，2015．

［6］ 郑思凡，杨冠鲁．换相重叠角的计算机仿真及辨识［J］．华侨大学学报（自然科学版），2009，30（3）：272－276.

［7］李捷．基于神经网络的轴承故障诊断技术研究［D］．成都：电子科技大学，2015．

［8］ 岑红蕾，鲁敏 基于 BP 神经网络的非线性函数逼近仿真研究［J］．农业网络信息，2015（1）：52－55．

［9］李新龙．基于人工神经元网络的系统辨识及其在汇率预测中的应用［D］．西安：西安交通大学，2003．

（责任编辑：朱联九）

Neural Network System Identification and Sample Modeling of Harmonic Sources

GUO Bao-ying1，ZHENG Si-fan2
(1.College of Engineering,Yang-En University,Quanzhou 362000,China;2.College of Mechanical and Electrical Engineering,Liming Vocational University,Quanzhou 362000,China)

Considering that the current power quality diagnosis and classification are dependent on a large number of sample acquisition for feature extraction,the normal generation process,transient concussion and short-circuit fault are made system identification by adopting system identification and taking three-phase direct current excitation generator system as research object.Then the type structure and training algorithm etc of the neural network are determined according to the actual situation of the problem and the simulation implementation is given.The simulation results show that the trained BP neural network has some generalization ability and can be used to model the fault samples with abnormal input parameters.

system identification；levenberg-marquardt；synchronous excitation generator；VC dimension；BP neural network

TM711

A

1673-4343（2017）04-0061-08

10．14098 ／j．cn35－1288 ／z．2017．04．011

2017-05-21

福建省中青年教师教育科研项目（JAT160588）；泉州市科技局项目（2014Z138）

郭宝英，女，福建泉州人，讲师。主要研究方向：电气控制。