基于小波包变换的脑电波诊断分析
王 伟,管 强,林 枫
(1.三明学院 信息工程学院,福建 三明 365004;2.三明市第一医院,福建 三明 365004)
基于小波包变换的脑电波诊断分析
王 伟1,管 强1,林 枫2
(1.三明学院 信息工程学院,福建 三明 365004;2.三明市第一医院,福建 三明 365004)
采用小波包分析法提取正常脑电波和发病脑电波的特征,构造特征向量,利用判别分析和聚类分析对脑电疾病特征进行判别分析和诊断分析。对三明市第一人民医院临床脑电数据进行实证分析,验证方法的实用性、准确性、高效性,为医生临床诊断发病区域提供科学依据。
脑电波信号;小波包分析;均值检验;判别分析;聚类分析
脑电波是人脑内部神经细胞群的点生理活动在大脑皮层的综合反映,将其记录下来,就是通常所说的脑电图(EEG)。脑电信号蕴含丰富的大脑活动信息,通过脑电图这个“窗口”,人们可以深入了解大脑的功能状态及其活动规律。脑电一般分为4个不同的基本节律(δ,θ,α,β节律)。在不同的生理或病理状态下脑电波节律有显著差异。通常考察脑电活动模式的一个重要途径是研究分析基本节律的特征[1]。目前在临床上很多医务工作者仍沿用传统的目检波形法,根据临床经验进行诊断效率低且有很强的主观性,研究客观有效的EEG分析诊断方法,一直是相关领域的研究热点。
目前脑电信号主要的特征提取方法有以下几种:(1)单一利用时域或是频域特征的方法[2]。如时域均值、频域能量等[3]。此方法虽然简单,但提取的特征太过单一,无法表征脑电信号的本质特征,因此分类正确率较低[4]。(2)传统时频域结合的方法。此方法只是将第一种方法提取的特征简单的组合以提供更多的特征,但仍然是一种平稳信号的分析方法,不适合用于描述非平稳的脑电信号[5-8]。(3)使用小波变换对脑电信号进行特征提取。此方法虽然适用于非平稳脑电信号,但是该方法仅仅是把脑电信号分解为低频和高频,在对低频继续分解成低频和高频,以此进行下去,却忽略了高频部分所含有的信息[9]。
本文采用小波包分析对脑电信号特征进行提取,小波包分析不仅在低频域对脑电信号特征提取效果优越,并且同时能够在高频域对脑电信号特征进行提取,使得脑电信号经过特征提取后信息损失达到最小。
1 小波包脑电信号特征提取
1.1 小波包变换
小波包变换的二尺度方程如下,其中h0k,h1k是多分辨分析中的滤波器系数:
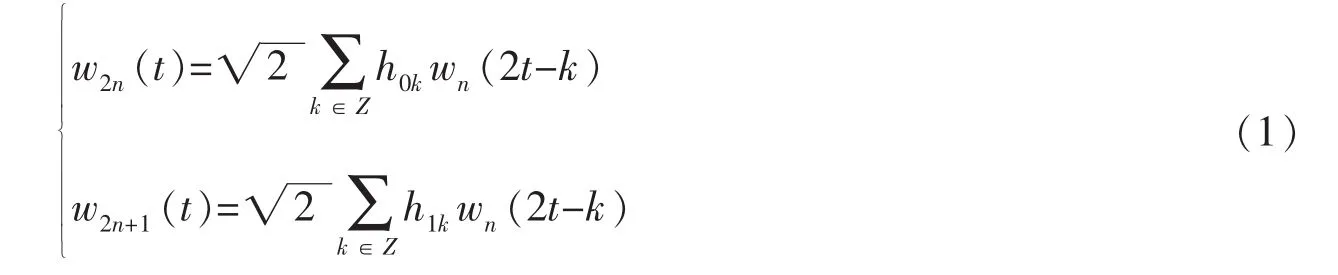
当 n=0 时,w0(t)=φ(t)为尺度函数,w1(t)=ψ(t)为小波函数。 定义函数序列 wn(t)n∈Z为由 w0(t)=φ(t)所确定的小波包。
根据小波包变换的性质,可以得到小波包系数递推公式为:

小波包分解的方法如图1所示,可见小波包分解不但对低频概貌空间进行分解,而且对高频细貌也进行了分解[10]。
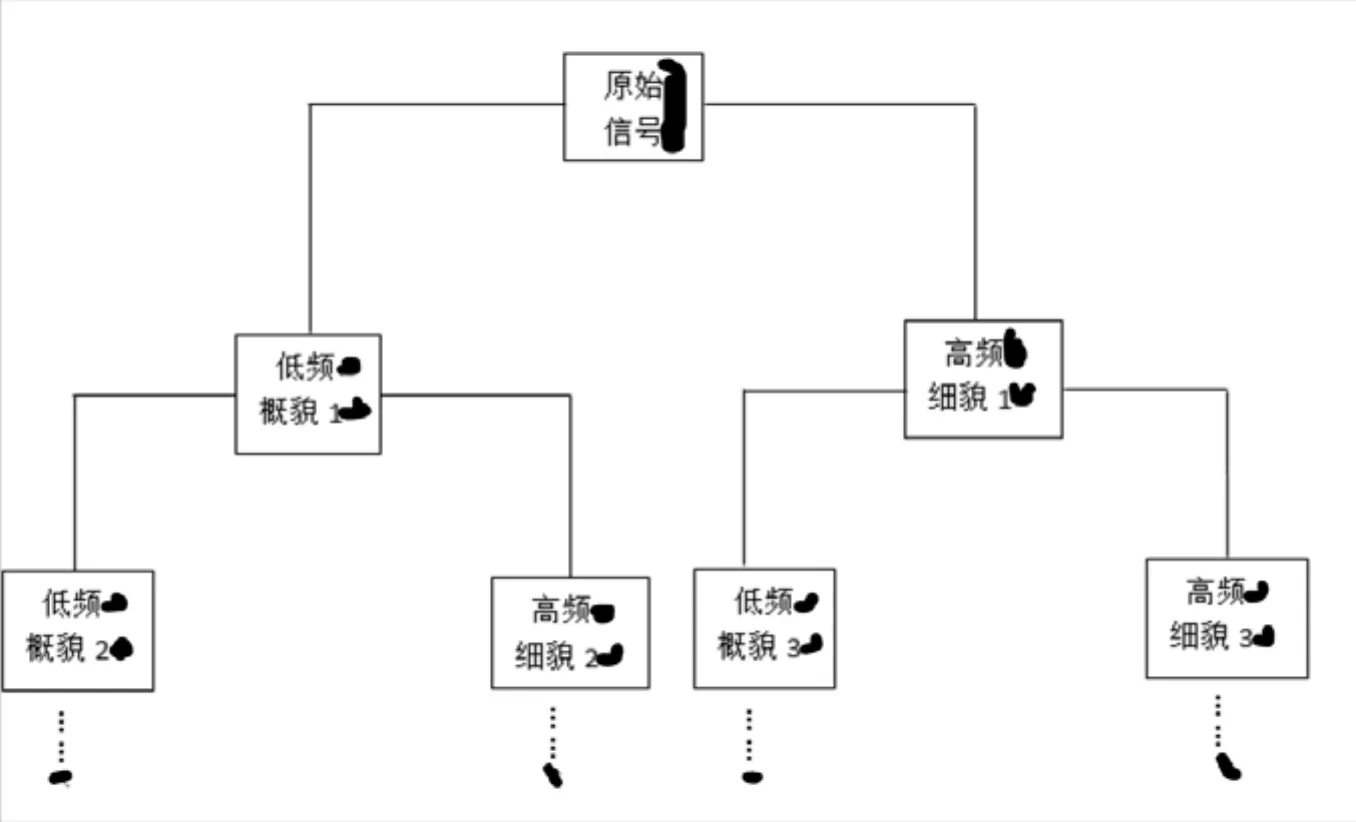
图1 小波包分解方法
1.2 小波包变换特征提取
由于脑电信号是非线性的非平稳信号,而小波包变换提供了一种能在频域和时域同时分析非平稳时变信号的特点,该方法采用小波包分解技术对每一段EEG数据进行低频和高频分解,得到所有频段的小波库。然而对给定的正交小波,一个长度为N=2L的信号进行分解方式最多可以有N=2L种,即一个深度为L的完整二叉树的子数目,该值往往比较大。在完整的二叉树结构中,并非所有二叉树都有价值。如何实现小波包最佳分解Coifman等人[11]提出了在小波包分解过程中的最佳基选择准则,其基本分解流程是一种类似于二叉树的结构,以划分后的子空间中的熵作为进一步划分的准则,当一个结点对应子空间中的熵大于该结点的下一级子结点对应的两个子空间的熵之和时,才接受该种划分,以此为划分准则,一直划分下去,直到不可再划分为止。另外,信息理论中的小波熵是用来对不确定性进行度量,应用到脑电信号号上,它能反应脑电信号在时域与频域上的能量分布特征[12]。
设E1,E2,…,Em为信号x(t)在m个尺度上的小波能谱,则在尺度域上的小波能谱可以形成对信号能量的一种划分。采取正交小波,可知在某一时间窗内(窗宽为W∈N)信号总能量E等于各分量Ej之和,即,式中Ej是小波熵,Shannon熵定义如下:

满足E(0)=0。其中s代表信号,si代表信号s在一个正交小波包基上的投影系数。
1.3 脑电信号特征提取
脑电波数据来源于三明市第一医院临床病例,见表1。通过MATLAB内置脑电波特征提取程序分别对18个电极测量出来的数据进行特征提取,采用3层分解(即n=3),正交过滤器选择“db5”,并以Fp1-A1为例进行特征提取。提取结果见表2~表4。
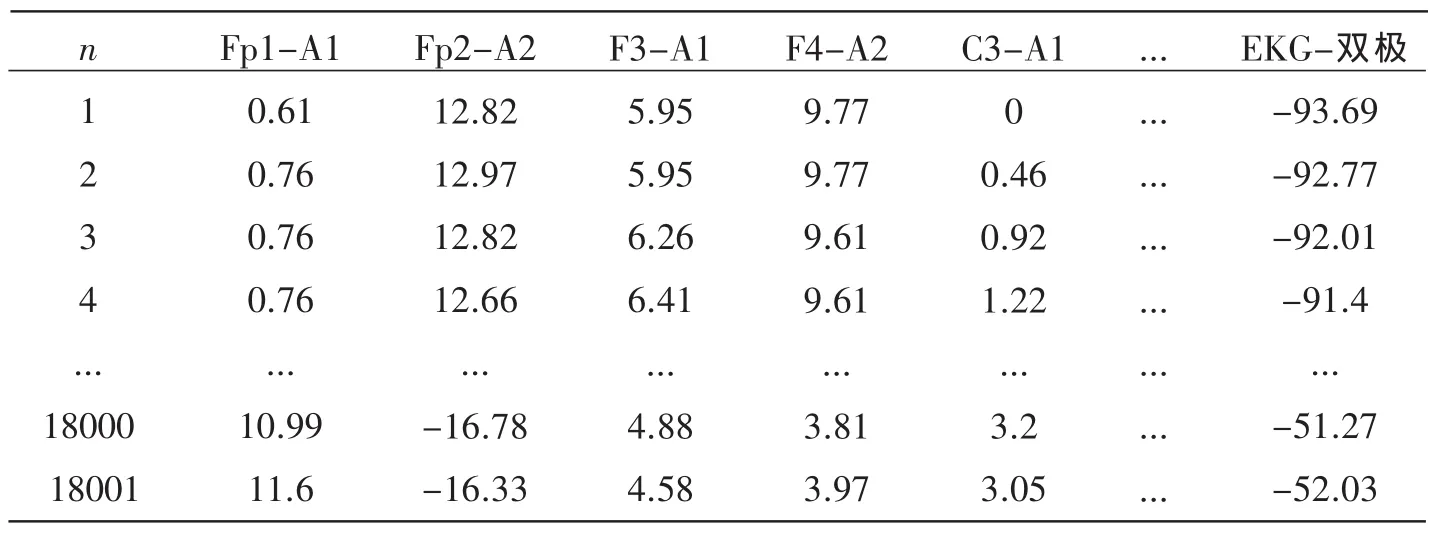
表1 正常小儿1的脑电图部分数据示例
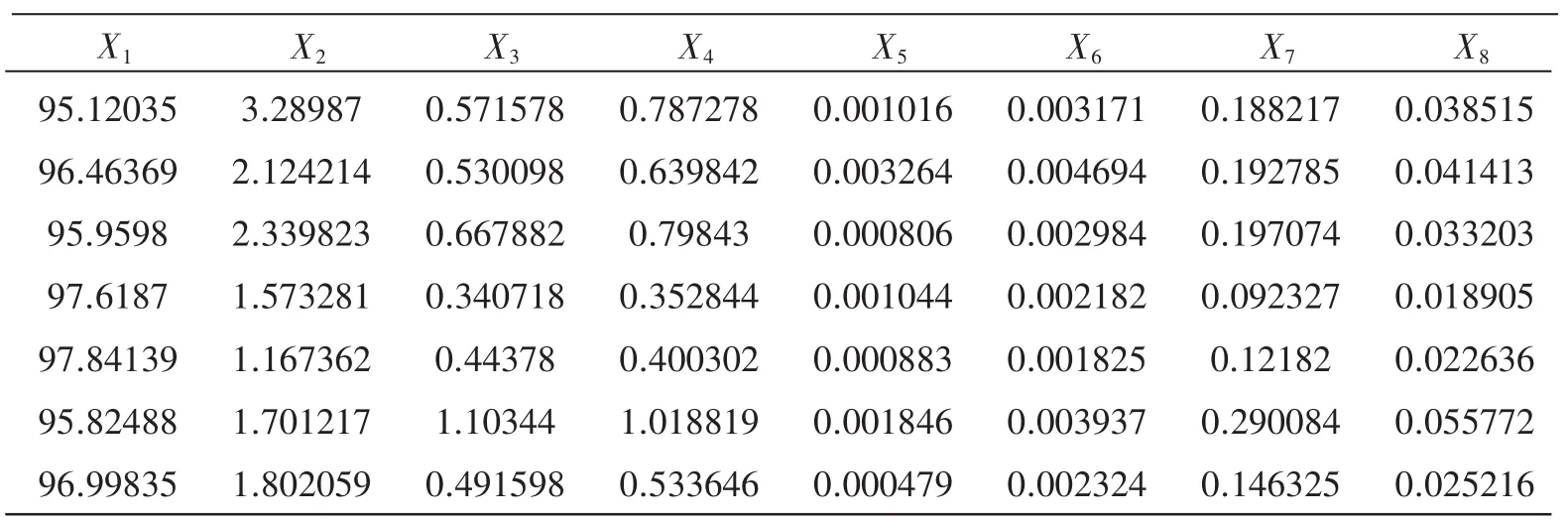
表2 正常小儿1的脑电特征向量
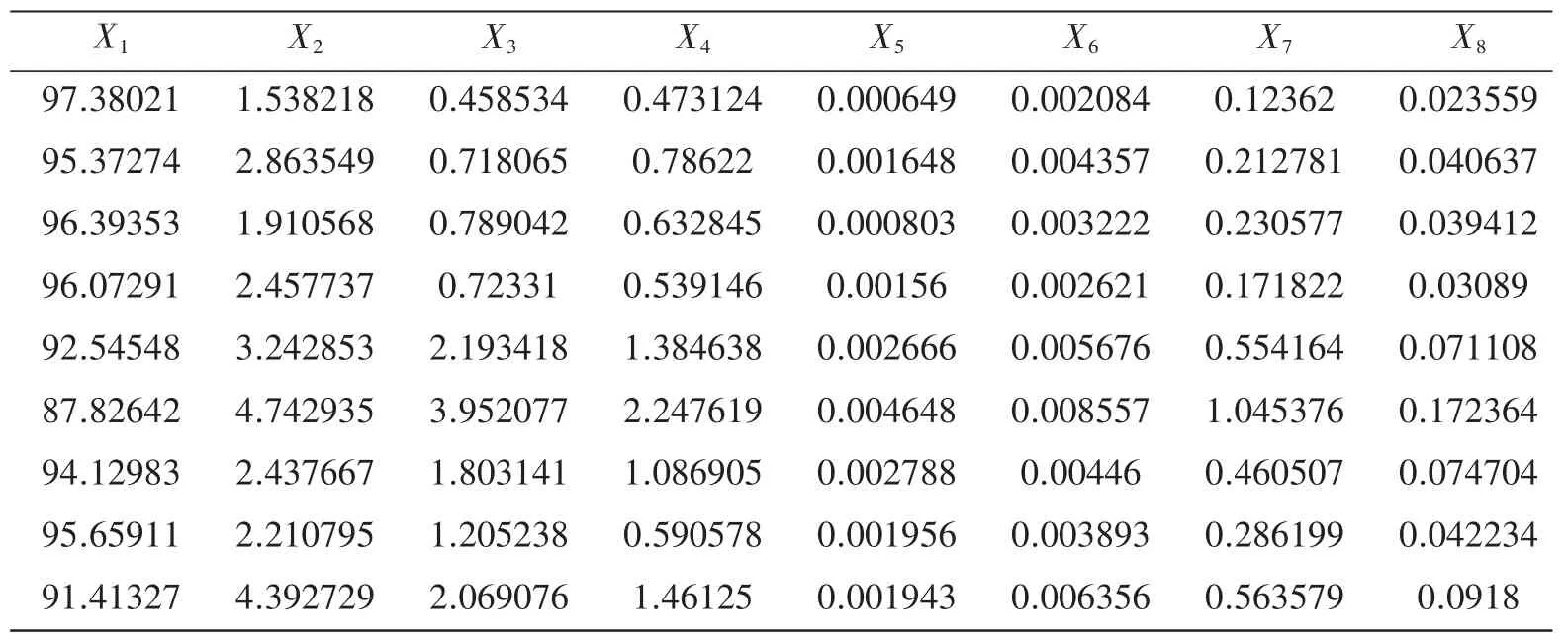
续表2
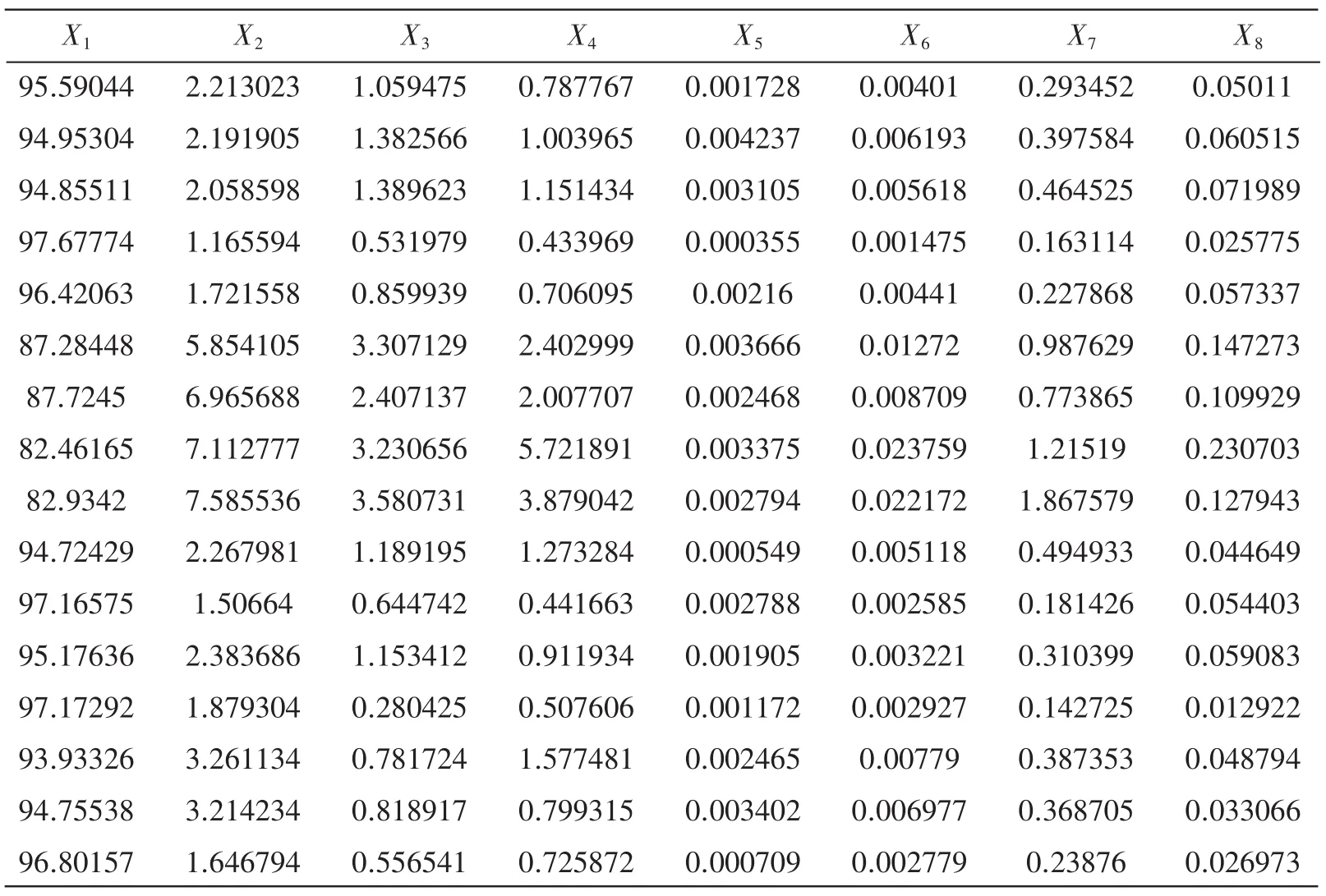
表3 正常小儿2的脑电特征向量
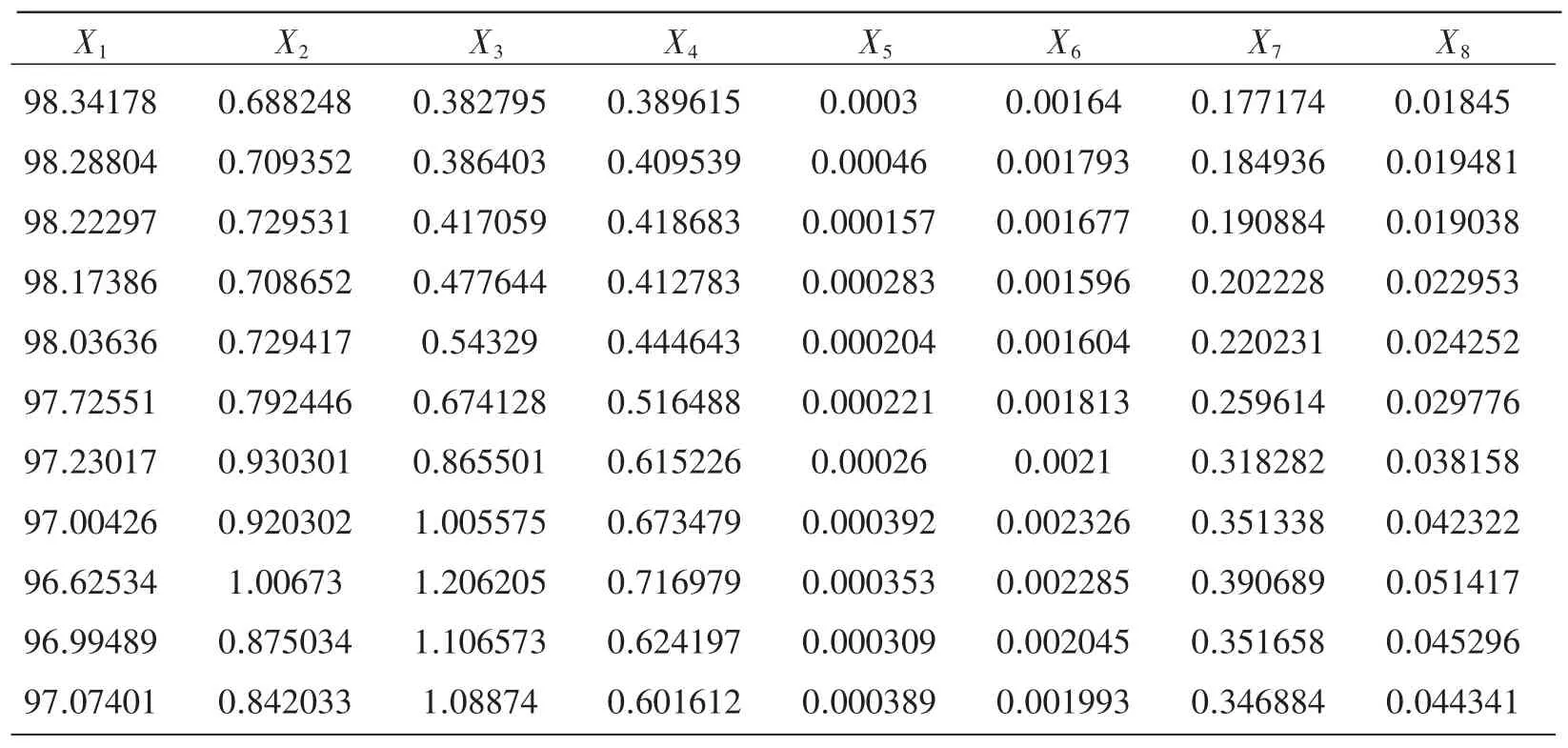
表4 患病小儿3的脑电特征向量
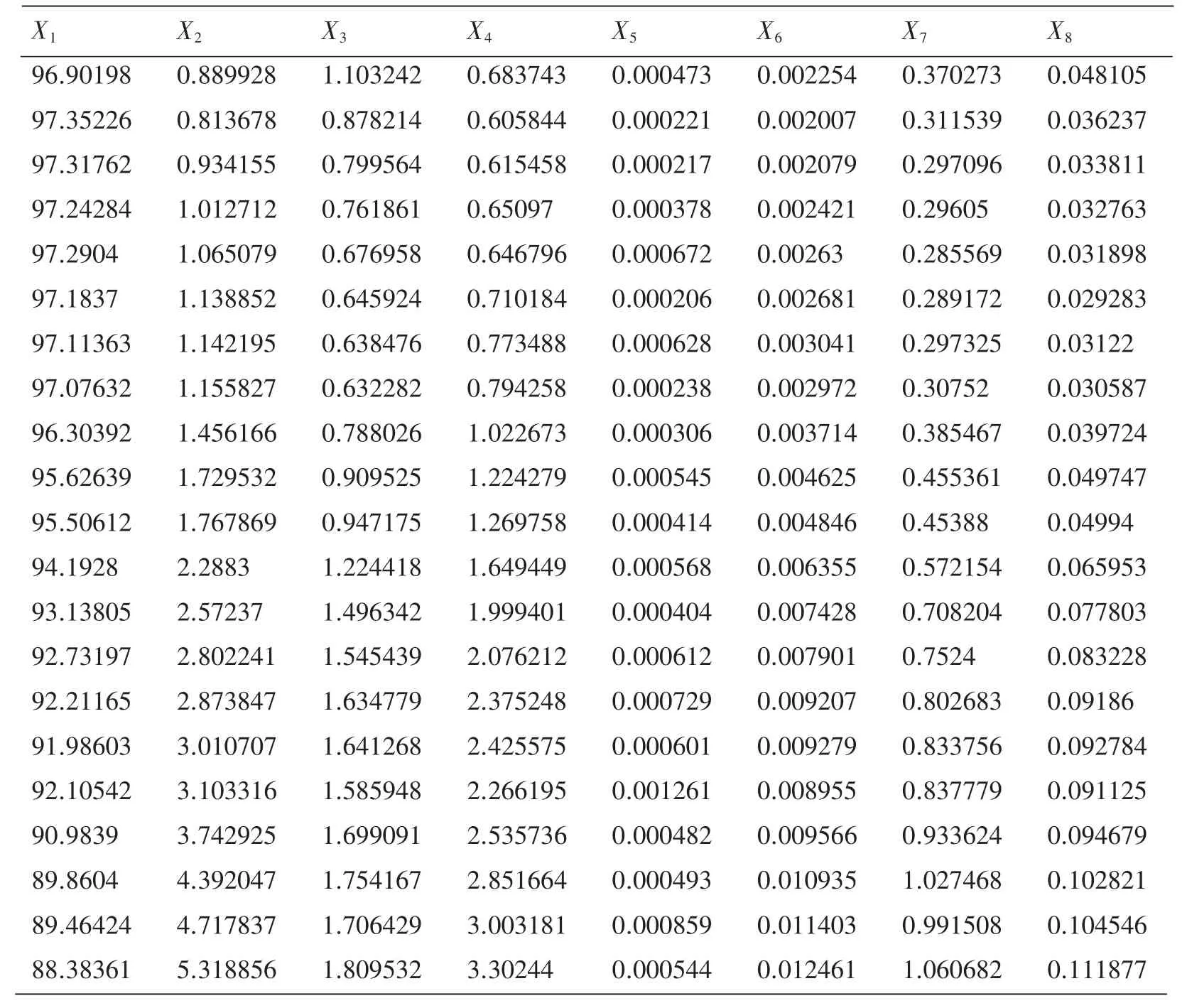
续表4
2 脑电信号特征向量检验
上面已对脑电数据进行了特征提取,得到一个8维的向量组,但是单从特征向量是无法直观的判定被测量者是否患有脑电疾病。为了更加科学,更加准确的对脑电疾病进行诊断,采用多元统计分析中的均值向量检验的方法来分析待诊断者的脑电特征向量与正常者的脑电特征向量是否存在明显差异。 若有显著性差异,则说明待诊断者患有某种脑电疾病,否则,说明待测者未患有脑电疾病。
为了验证均值检验方法的有效性,在已知小儿1和小儿2都为正常儿童的情况下,进行模拟检验。 设小儿1为已知未患有脑电疾病的儿童,小儿2为待诊断是否患有脑电疾病儿童。应用SPSS统计分析软件进行假设检验[14],结果见表5。
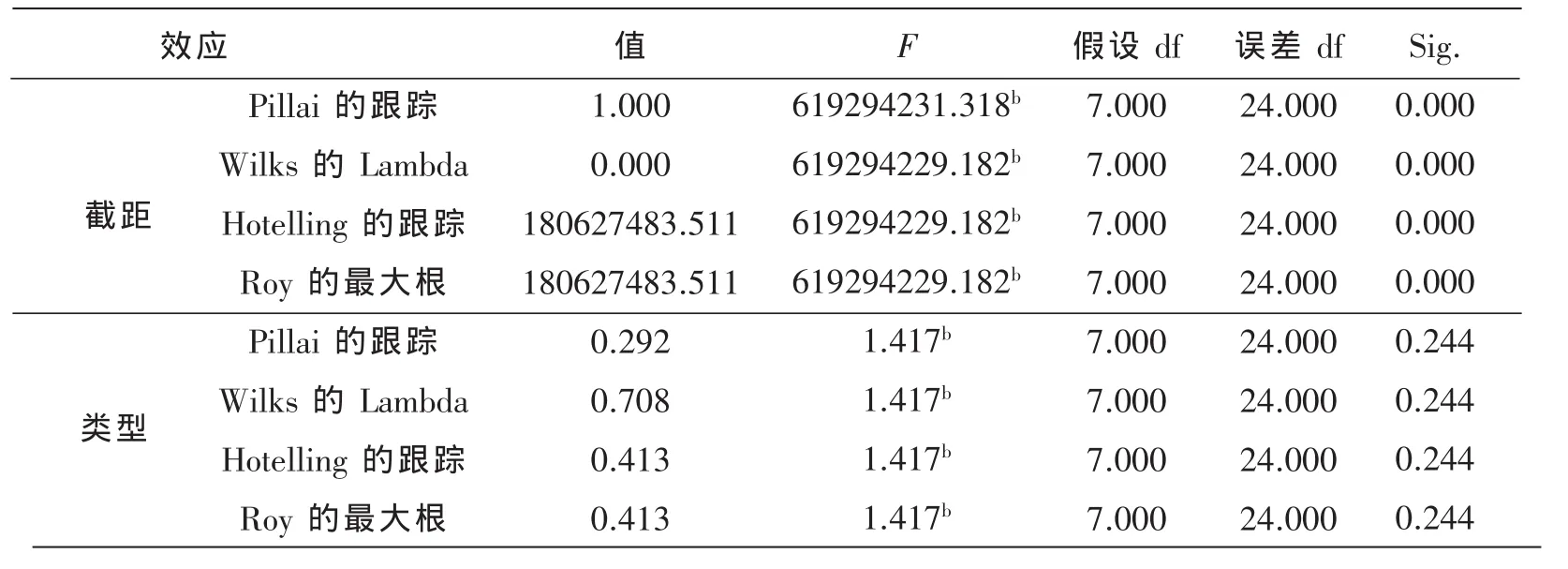
表5 多变量检验a
由结果可见,在α=0.05的水平下,接受原假设H0。 说明小儿1和小儿2的脑电无明显差异,结果与预期的完全一致。说明均值检验的方法对脑电疾病诊断有很好的效果。
在判定小儿2为正常儿童后,将小儿2的脑电数据分类为正常小儿脑电数据,在以后判定其他小儿是否患有脑电疾病时,小儿2纳为训练样本,这样做的好处在于能够不断的丰富正常小儿的脑电数据,以建立正常小儿脑电数据信息库,对后期判定的准确性会不断的增加。
在已知小儿3患有某种脑电疾病,并且发病区域为Fp1-A1来测试均值检验方法能否准确判定该儿童为患有脑电疾病的患者。检验结果见表6。
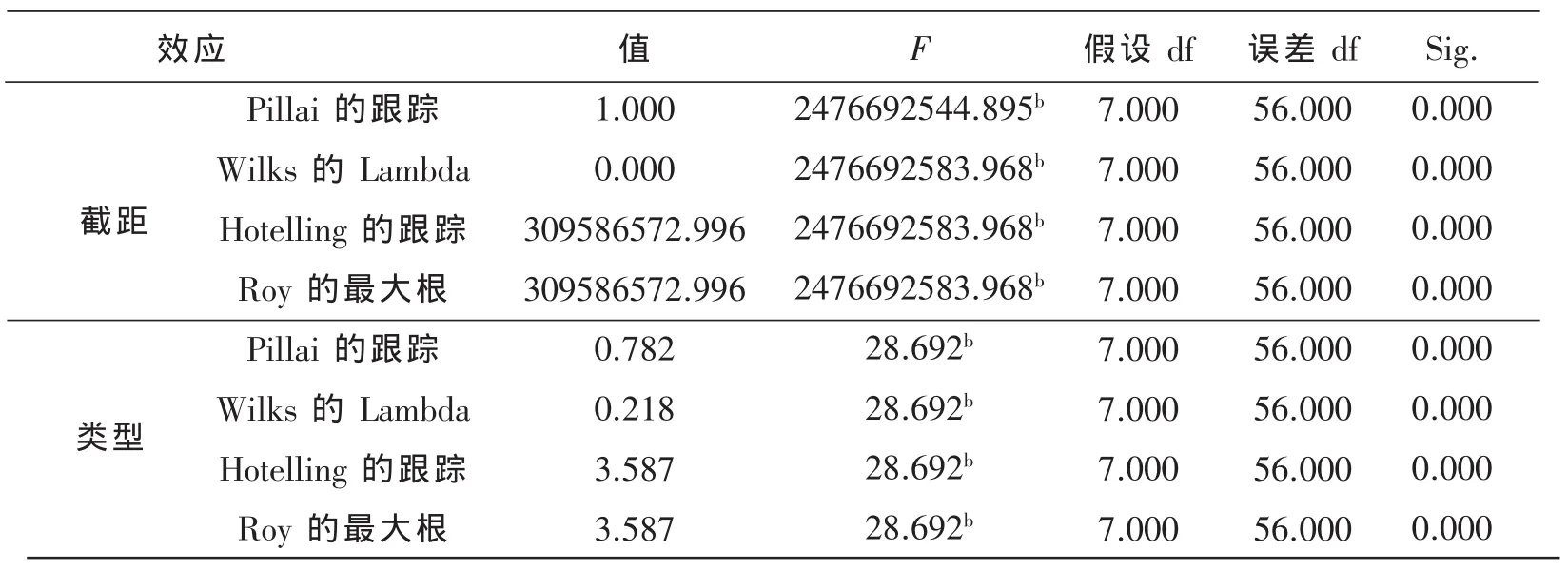
表6 多变量检验a
结果显示在α=0.05的水平下,拒绝原假设H0,说明小儿3的脑电数据与正常小儿的脑电数据相比显著异常。与预期结果相同,进一步证明均值检验的方法对是否患有脑电疾病的判定有非常好的效果。
3 脑电疾病贝叶斯判别分析诊断
虽然上节均值检验的方法能够对是否患有脑电疾病进行判别,但是不能确诊患病者所得具体哪种疾病。 因此在均值检验病人患有脑电疾病时,还需确定病人患有何种疾病。从而给患者提供针对性的治疗,提高治疗效果。 而贝叶斯判别分析法对分类具有高效准确的特性,故本文采用贝叶斯判别分析法对患有脑电疾病的患者进行类别的判定,以确定该患者具体患有哪种脑电疾病。具体操作如下:这里假设该患者患有的脑电疾病为已知的(也就是说医院有该疾病的相关数据)。
应用小波包分析的方法对正常小儿和发病小儿的Fp1-A1进行脑电特征提取,得到一个8维的向量组;其中正常小儿脑电特征向量数据见表7,已知发病小儿脑电特征向量数据(病1、病2)见表8~9;和待判定患有何种疾病的发病小儿脑电特征向量数据见表9的最后一行。
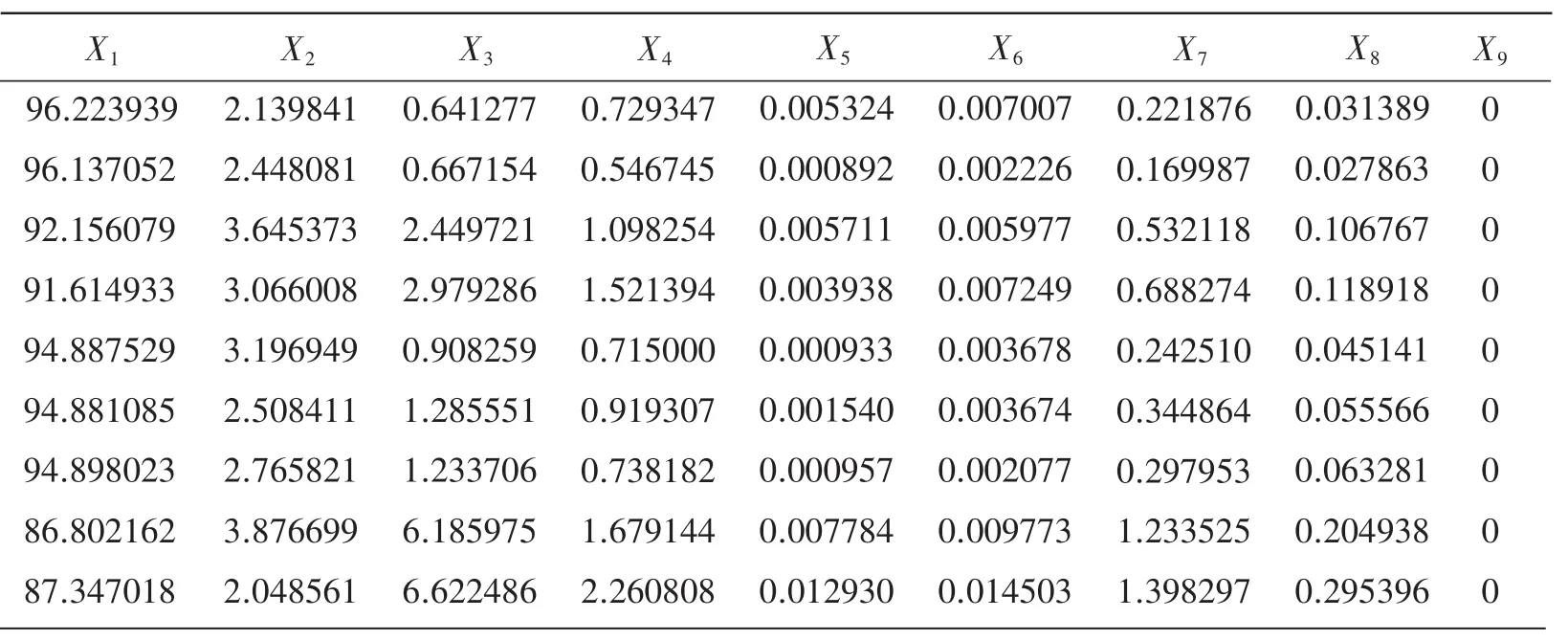
表7 正常小儿
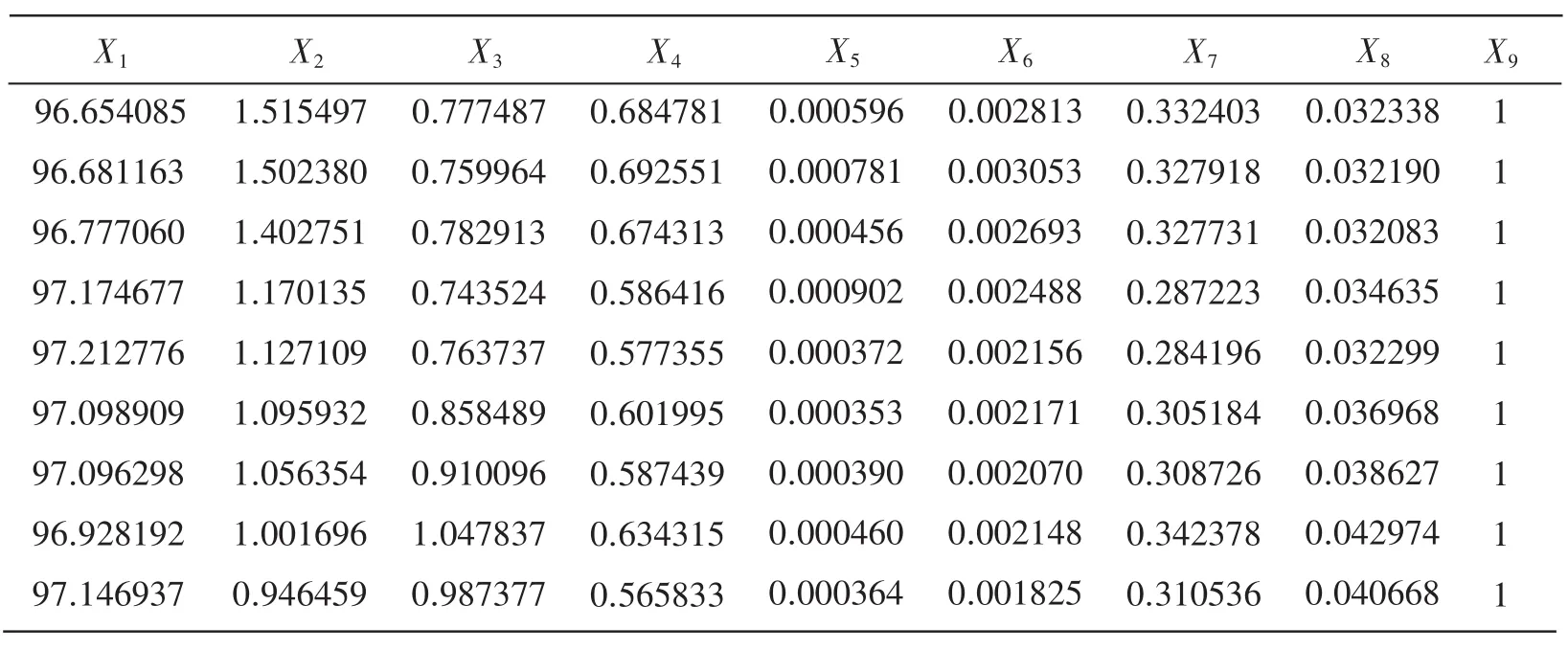
表8 发病小儿(病1)
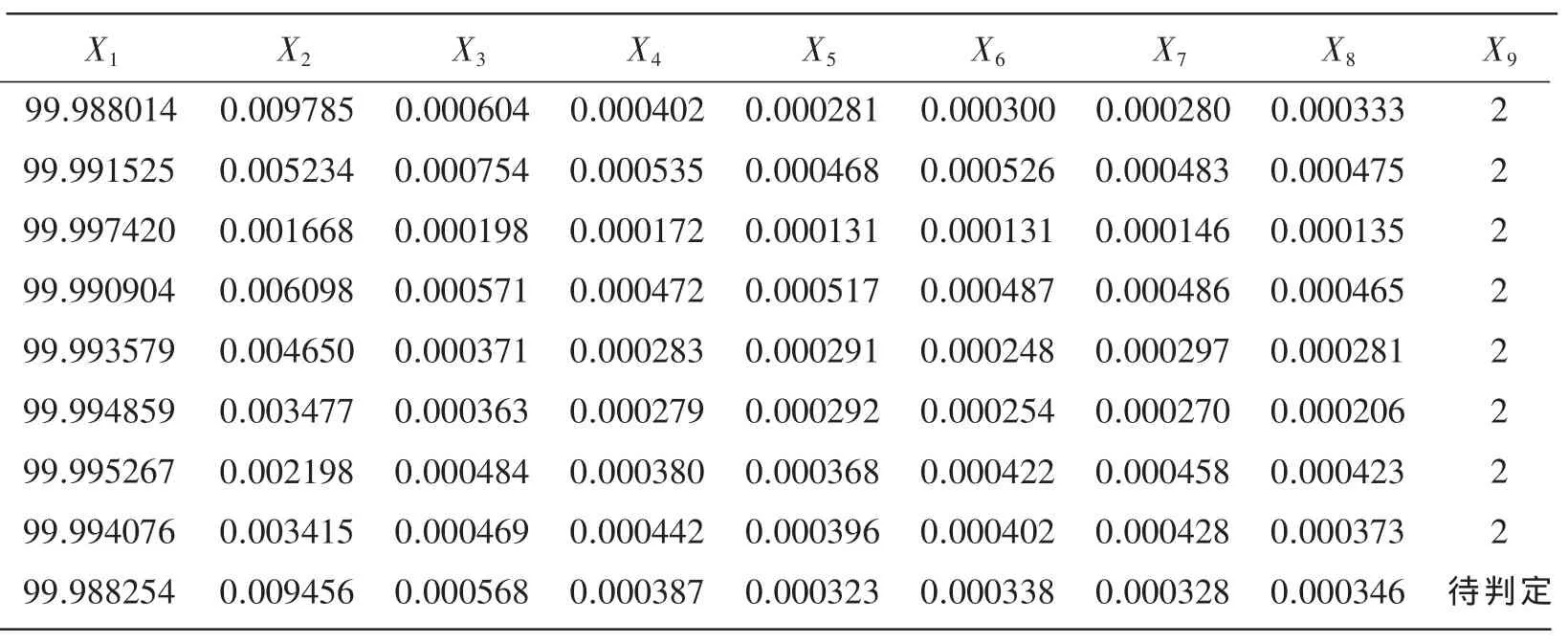
表9 发病小儿(病2)
对表9的数据进行判别分析得到的结果为(见表10)。
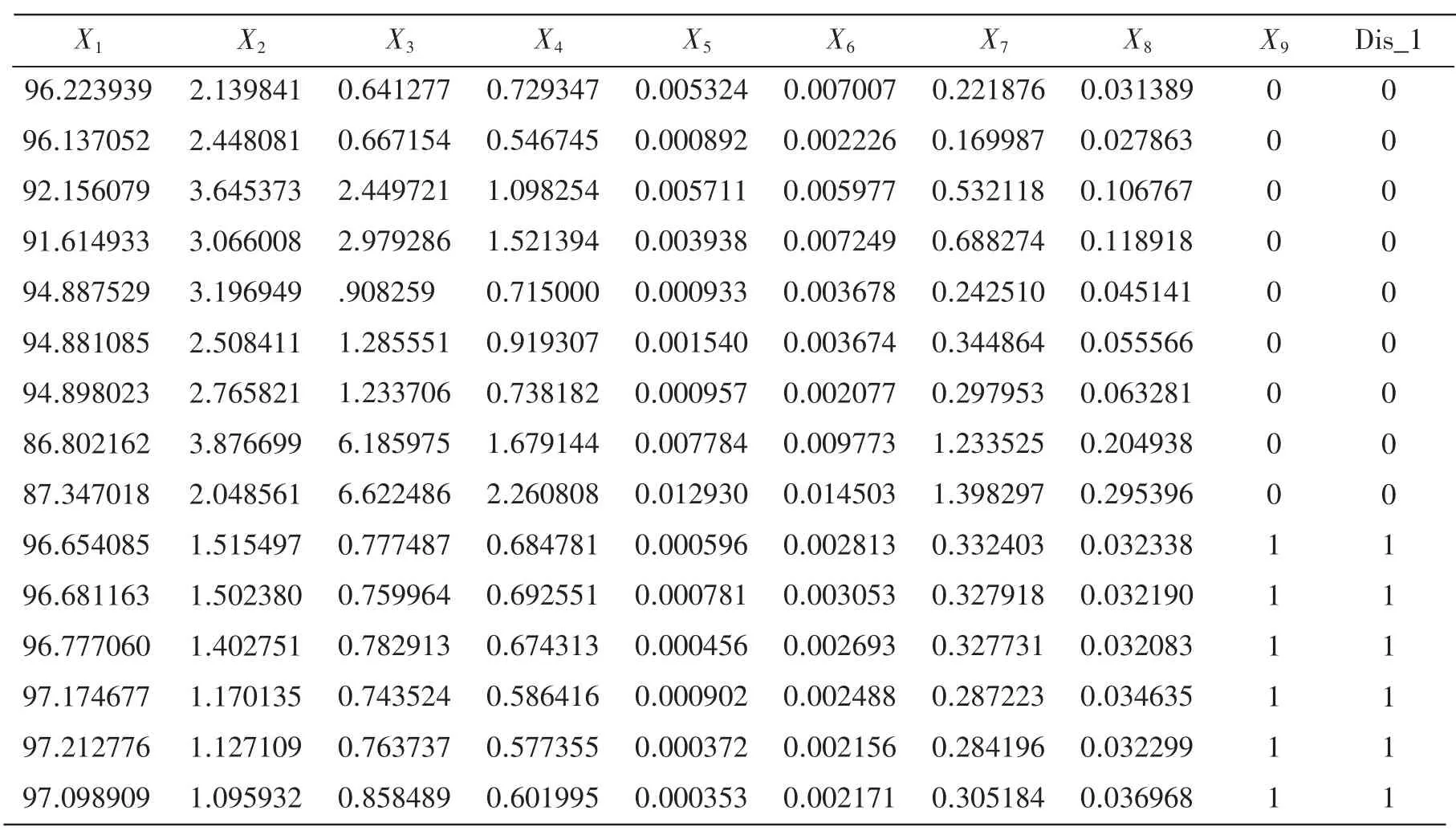
表10 判别结果
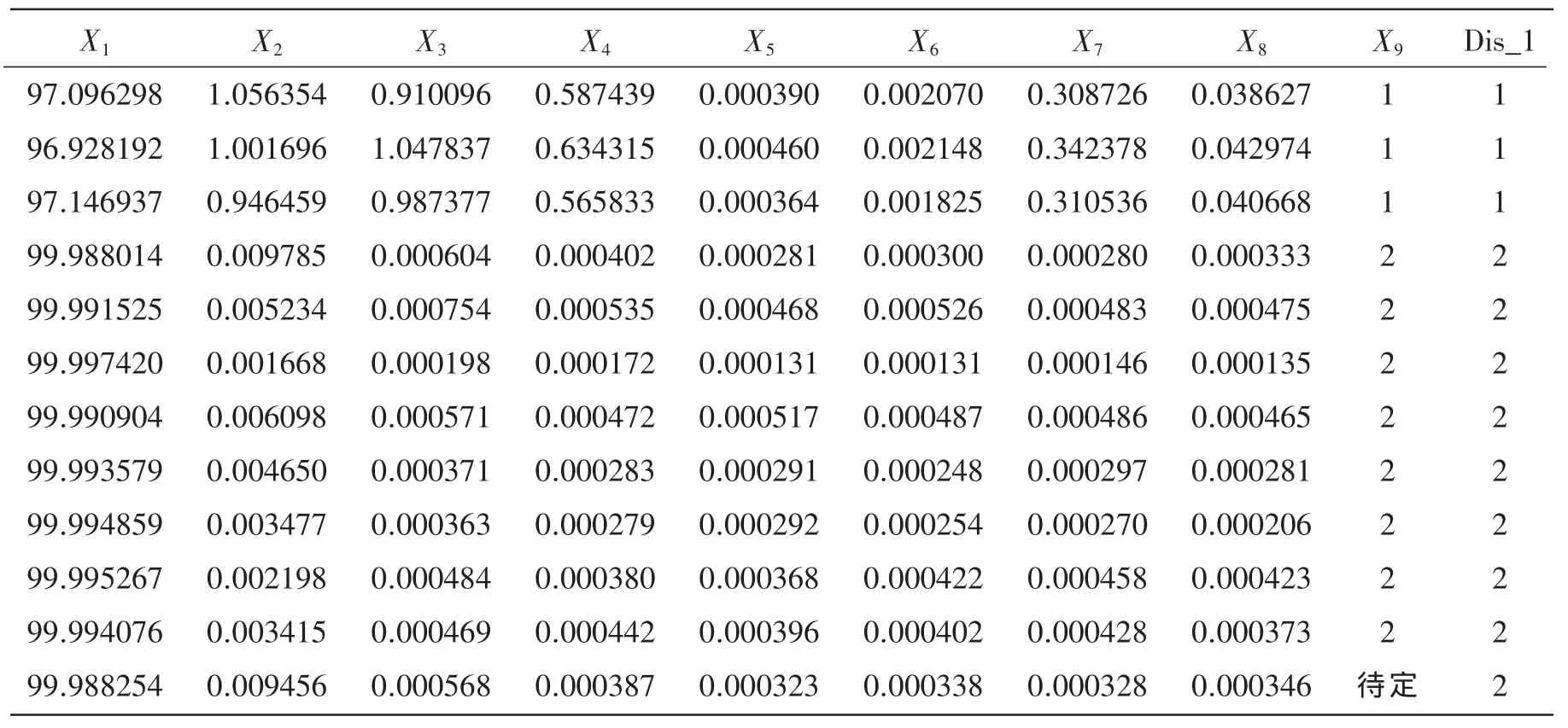
续表10
从表10可见,判别分析的方法准确的将待判定样本归为病2类,故判别分析的方法对于判定患者患有哪种脑电疾病具有指导性意义。
4 脑电疾病聚类分析诊断
利用判别分析方法对患者患何种疾病能进行有效诊断,但是实际当中待检查者患有的脑电疾病有可能是一种新型病,医院的以往病例中并未有此病的相关记录,此时判别分析法就不再适用。为了克服该问题,采用聚类分析方法进行诊断。为了检验聚类分析对脑电疾病诊断的实用性,本文针对正常小儿、发病小儿和间期异常发电小儿的T4-A2区域进行特征提取后聚类分析。提取结果见表11。
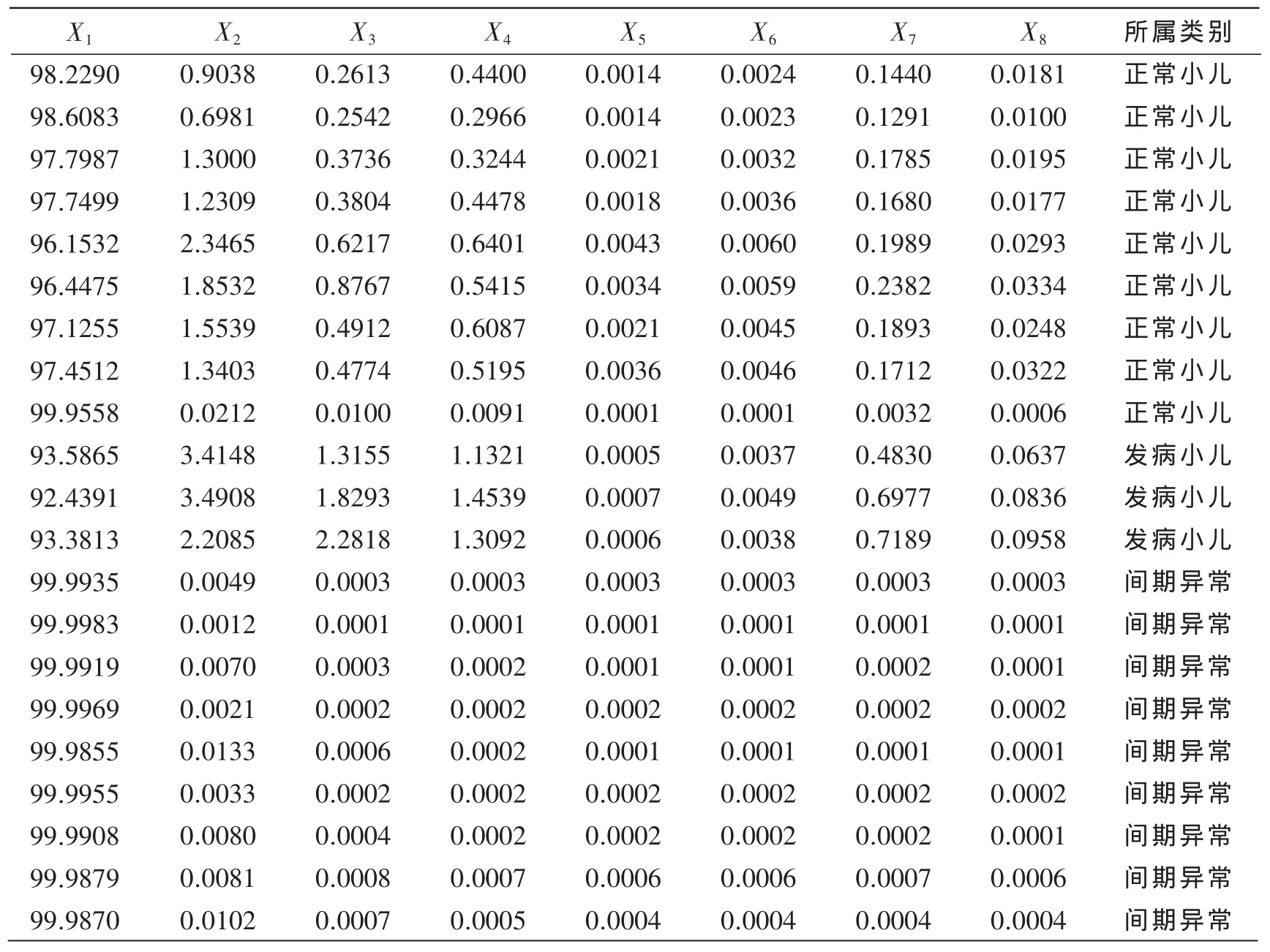
表11 3种小儿脑电特征向量提取结果
对表11的数据进行聚类分析得到的树状图如图2。
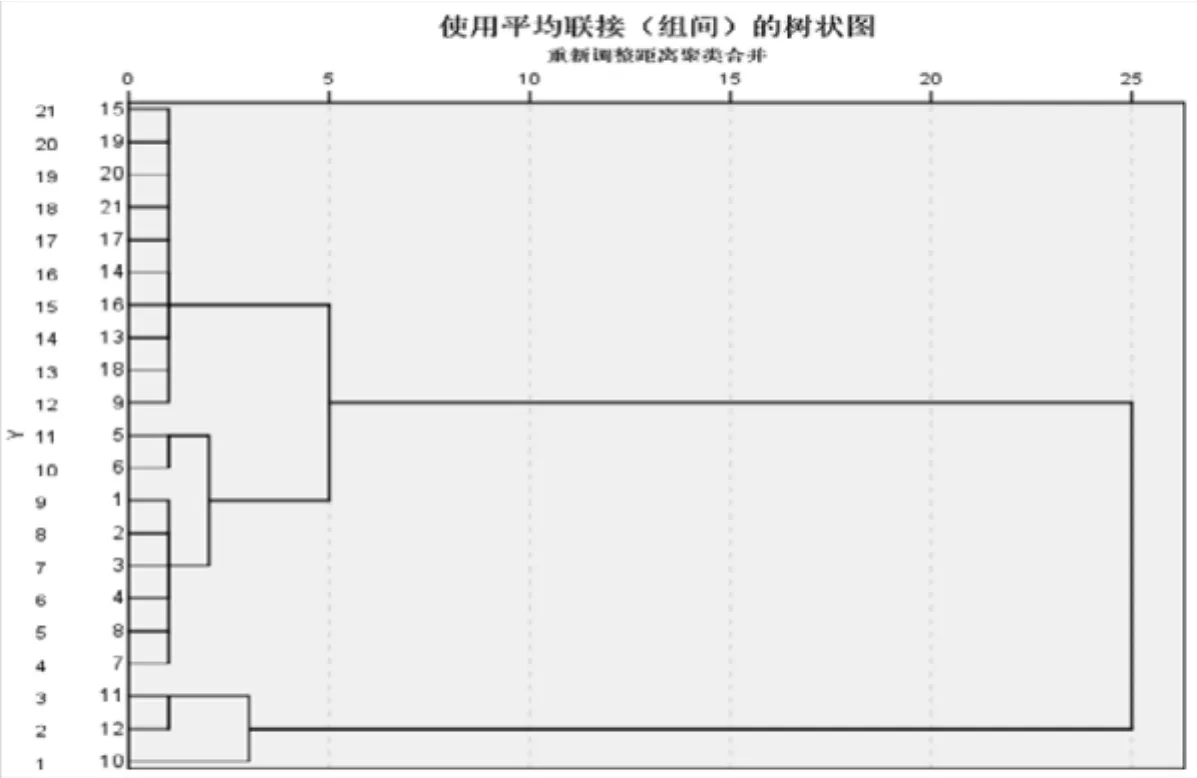
图2 聚类分析树状图
从图2中可以看出,聚类分析能够很好的自动将脑电疾病分类,这对于在没有训练样本的情况下也能够很好的判定疾病,这为医生提供了较好针对性治疗的科学依据。
5 结论
采用小波包分析法对正常脑电波和发病脑电波的特征进行提取,构造特征向量,有效对繁杂脑电数据进行了信息提取。对三明市第一人民医院临床脑电数据利用判别分析和聚类分析对脑电疾病特征进行判别分析和诊断分析,克服传统医生目测法的主观性,提高了脑电图诊断的精确率。 该方法的实用性、准确性、高效性,为医生临床诊断发病区域提供科学依据。
[1] 杨仁桓,宋爱国,徐宝国.基于谐波小波包变换的脑电波基本节律分析[J].东南大学学报,2008,38(6):996-999.
[2] 王兆源,周龙旗.脑电信号的分析方法[J].南方医科大学学报,2000(2):189-190.
[3] 黄思娟,吴效明.基于能量特征的脑电信号特征提取与分类[J].传感技术学报,2010,23(6):782-785.
[4] 李明远,李晓红,李树春.脑性瘫痪小儿 100 例脑电波分析[J].黑龙江医药科学,1989(1):18-20.
[5] 李卓,高小榕.稳态体感诱发电位的提取与分析[J].清华大学学报,2006,46(6):861-864.
[6] 高玉娜.小儿额叶癫痫的临床与脑电图特征分析[J].中外医疗,2014(26):84-85.
[7] 张胜,乔世妮,王蔚.抑郁症患者脑电复杂度的小波熵分析[J].计算机工程与应用,2012,48(4):143-145.
[8]戴冷湜.脑电信号的特征提取与分析方法研究[D].杭州:浙江大学,2011.
[9]王攀.基于小波变换和多域融合的脑电信号特征提取[D].杭州:浙江大学,2011.
[10] 王淑娟,陈博,赵国良.基于小波包变换预处理的模拟电路故障诊断方法[J].电工技术学报,2003,18(4):118-122.
[11] COIFMAN R,WICKERHAUSER M V.Entropy-based algorithms forbest-basis selection[J].IEEE Trans Inf Theory,1992,38:713-718.
[12] 王登,苗夺谦,王睿智.一种新的基于小波包分解的 EEG 特征抽取与识别方法研究[J].电子学报,2013,1(1):193-198.
[13] 朱建平.应用多元统计分析[M].北京:科学出版社,2012:31.
[14] 程莹,陈希镇.巧用 SPSS 进行均值的假设检验[J].统计决策,2008(18):155-156.
[15] 王骏,王士同,邓赵红.聚类分析研究中的若干问题[J].控制与决策,2012,27(3):321-328.
[16] 沈小伟,王飞跃,程长建,等.聚类分析方法在企业班组管理中的应用[J].自动化学报,2012,38(4):563-569.
(责任编辑:朱联九)
Brain Wave Diagnosis Analysis Based on Wavelet Packet Transform
WANG Wei1,GUAN Qiang1,LIN Feng2
(1.Institute of Information Engineering,Sanming University,Sanming 365004,China;2.Sanming First Hospital, Sanming 365004,China)
In this paper,the wavelet packet analysis method is used to extract the feature of normal brain waves and the onset brain waves and construct the feature vector.Meantime,discriminant analysis and cluster analysis are used to identify patient's disease with EEG features.The empirical analysis is performed based on the clinical EEG data of the First People's Hospital of Sanming City in order to verify the method's practicability,accuracy and efficiency.The method can provide scientific basis for the clinical diagnosis of the doctor.
brain wave signal;wavelet packet analysis;means test;discriminant analysis;cluster analysis
R311
A
1673-4343(2017)04-0025-09
10.14098 /j.cn35-1288 /z.2017.04.005
2017-03-31
国家青年自然科学基金项目(11401341);福建省自然科学基金项目(2015J05014);2015福建省高校杰出青年科研人才培育计划,福建省高校新世纪优秀人才支持计划([2016]23号);国家级大学生创新创业训练计划项目(201511311002);福建省大学生创新创业训练计划项目(201411311046);重复经颅磁刺激结合长程视频脑电图监测治疗癫痫的研究(2015-s-1(6))
管强,男,江西上饶人,副教授,博士。主要研究方向:应用统计。

