基于三维电气几何模型输电线路绕击跳闸率的计算
李 博,鲁志伟,贾 茹,宋庆秋
(1.国网内蒙古东部电力有限公司 电力科学研究院,内蒙古 呼和浩特 010020;2.东北电力大学 电气工程学院,吉林 吉林 132012;3.国网吉林省电力有限公司 通化供电公司,吉林 通化134001)
基于三维电气几何模型输电线路绕击跳闸率的计算
李 博1,鲁志伟2,贾 茹2,宋庆秋3
(1.国网内蒙古东部电力有限公司 电力科学研究院,内蒙古 呼和浩特 010020;2.东北电力大学 电气工程学院,吉林 吉林 132012;3.国网吉林省电力有限公司 通化供电公司,吉林 通化134001)
由于山区地形复杂,准确计算绕击跳闸率较为困难。现有的传统二维电气几何模型法,在对绕击率进行计算时,取导地线平均高度,这只能反映线路整体水平,并不能表示线路某一段的实际情况,特别是对于大档距的输电线路来说,若采用平均高度进行计算,可能会得到该档距内绕击率较小的结论,但实际上在该档距内某一段线路绕击率是很大的。因此,结论存在较大误差,对二维电气几何模型的改进是十分必要的。在二维电气几何模型的基础上,进行三维拓展,将线路上每一点的对地高度都进行了分析计算,给出了在三维电气几何模型下的绕击跳闸率计算公式;并以通化地区220 kV线路为例,比较两种方法计算结果,结果表明三维电气几何模型与实际更相符。
大档距;绕击跳闸率;二维电气几何模型;三维电气几何模型
据统计,国内220 kV及以上线路雷电绕击跳闸越来越严重[1]。华东地区220 kV及以上线路在满足有效屏蔽前提下,处于平原的杆塔仍然会遭受雷电绕击。近几年,国内特高压输电线路蓬勃发展,而特高压线路雷击跳闸主要原因是雷电绕击。因此,准确计算输电线路绕击跳闸率对电力系统稳定运行具有极其重要的意义。输电线路的雷电绕击率通常与地形地貌、避雷线保护角等因素有关。传统的经典电气几何模型(EGM)虽然引入了击距的概念,考虑了雷击线路的过程[2-6],与实际情况较为相符,但其仍然以导线平均高度代入计算,存在一定误差[7-9]。本文对电气几何模型进行改进,考虑了导地线每一点的对地高度[10-11],编写了绕击跳闸率的三维计算程序。
1 二维电气几何模型
二维电气几何模型考虑雷电先导的下行过程,根据在先导头部靠近地面后进入某个暴露弧确定击中部位。因此,该模型是一种考虑雷击机理并与实际数据较为符合的一种方法。雷电先导入射角分布密度函数计算公式为[11]:
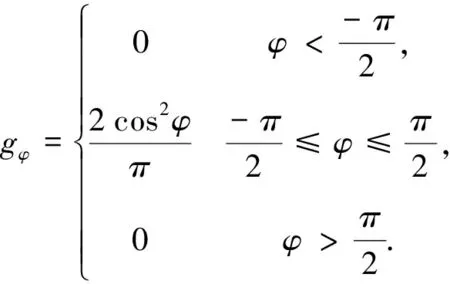
(1)
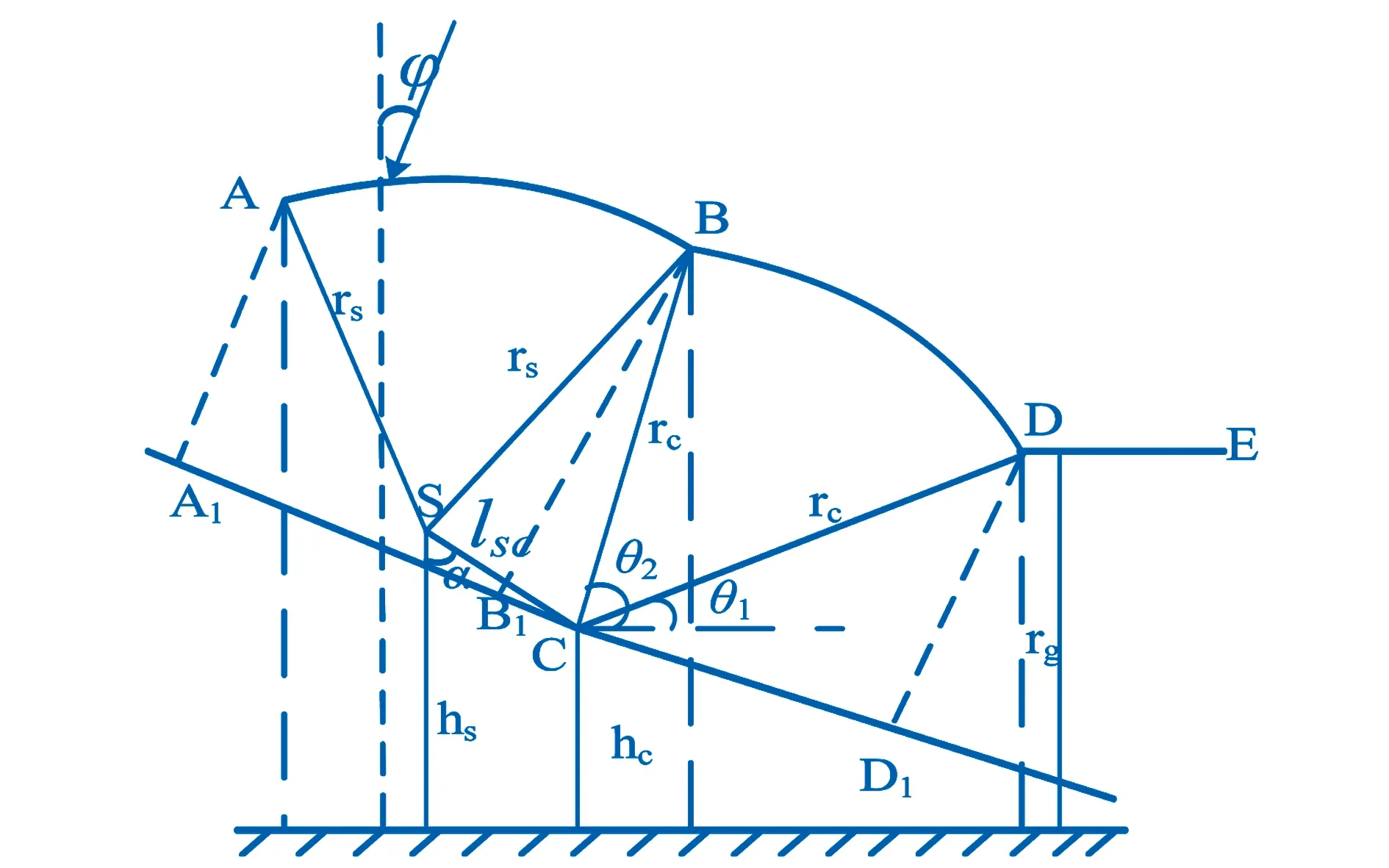
图1 二维电气几何模型
在考虑雷电先导入射角时,二维电气几何模型如图1所示。在图1中,S表示避雷线,C表示导线,φ表示先导入射角,rs表示避雷线击距,rc表示导线击距,rg表示地面击距,以S、C为圆心,rs、rc为半径分别画圆,交于B点;距地高度为rg处作一水平线DE,和以C为圆心的圆交于点D;A点为两避雷线中垂线与弧AB的交点。hs为避雷线平均高度,hc为导线平均高度,α为保护角,弧AB为屏蔽弧,其在垂直于先导入射角的平面投影lA1B1为屏蔽宽度,弧BD为暴露弧,其在垂直于先导入射角的平面投影lB1D1为暴露宽度,绕击率计算公式为:
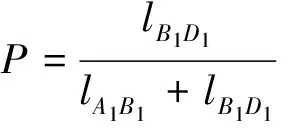
(2)
由于rs、rc、rg都与雷电流幅值成正相关,雷电流幅值越大,暴露弧越小,当雷电流幅值达到某一数值时,暴露弧为0,此时将不会发生绕击。因此,该雷电流被称为最大绕击雷电流Imax。
在确定最大绕击雷电流后,传统电气几何模型绕击跳闸率计算公式为:
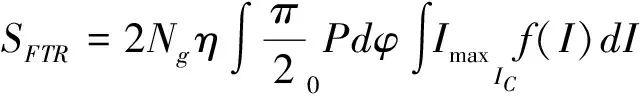
(3)
式中:Ng为落雷密度[次/(km2·年)];η为建弧率;f(I)为雷电流概率密度函数;I为绕击雷电流;IC为最小闪络雷电流;Imax为最大绕击雷电流。
由于此模型利用的是避雷线导线的平均高度,利用此公式计算得到的绕击跳闸率只能反映线路的整体水平,对于山区档距很大的区段,沿着线路方向每一点的绕击率有所差别,这样累积起来误差会较大,导致不能反映线路的真实绕击耐雷性能,因此有必要对此模型进行改进。
2 三维电气几何模型
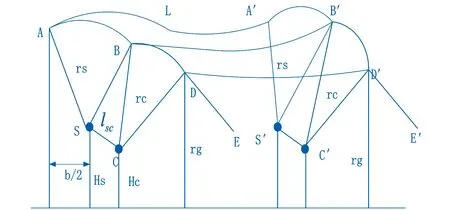
图2 三维电气几何模型
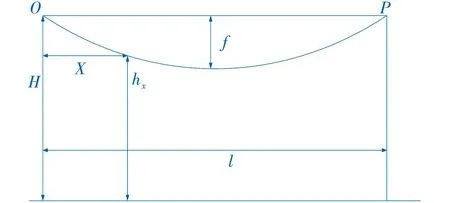
图3 平原地区导地线高度示意图
三维电气几何模型,如图2所示。按照图1的作图方法,在档距内每一点作图,最终得到图2。在图2中,AA′B′B为保护弧面,若雷电先导先到达此面,则击中避雷线,导线被保护;BB′D′D为暴露弧面,若雷电先导先到达此面,则对导线放电,此时避雷线保护作用失效;若雷电先导先到达DD′E′E面,则向大地放电。由于rs、rc、rg都与雷电流幅值成正相关,雷电流幅值越大,暴露弧面BB′D′D越小,当雷电流达到最大绕击雷电流时,暴露弧面BB′D′D将变为0,此时将不会再发生绕击。
2.1 平原绕击三维分析
在图3中,O点和P 点表示避雷线或导线悬挂点,H表示悬挂点对地高度,f表示避雷线或导线弧垂,hx表示避雷线或导线任意一点对地高度,则避雷线或导线任意一点对地高度公式为[9]:
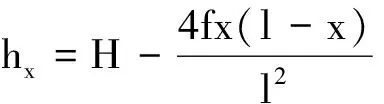
(4)
在任一雷电流作用下,图2中雷击暴露宽度为:
lBxyDxy=rccos(θ1+φ)xy-rccos(θ2+φ)xy,
(5)
(θ1)xy与(θ2)xy意义与图1中的θ1和θ2相同,但是已经沿着线路方向拓展,随着导地线高度变化而变化,经推导可得:
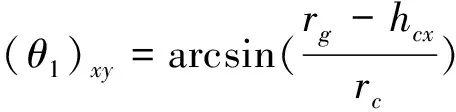
(6)
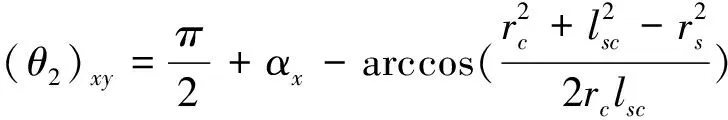
(7)
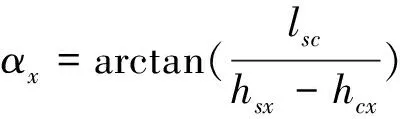
(8)
输电线路最大击距公式为[10]:
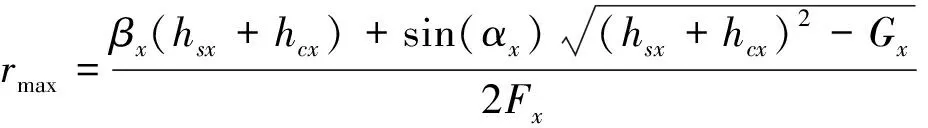
(9)
式中:Fx=βx2-sin2(αx);Gx=Fx((hsx-hcx)/cos(αx))2。
发生绕击闪络的最大雷电流幅值为[10]:
Imax=(0.1rmax)1.54 .
(10)
由上述公式可以得到平原地区输电线路在单个档距内任意截面绕击率:
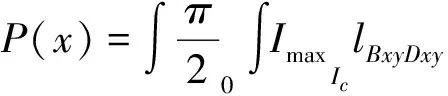
(11)
总绕击跳闸率为:
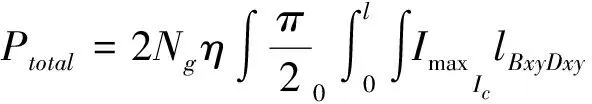
(12)
2.2 山区绕击三维分析
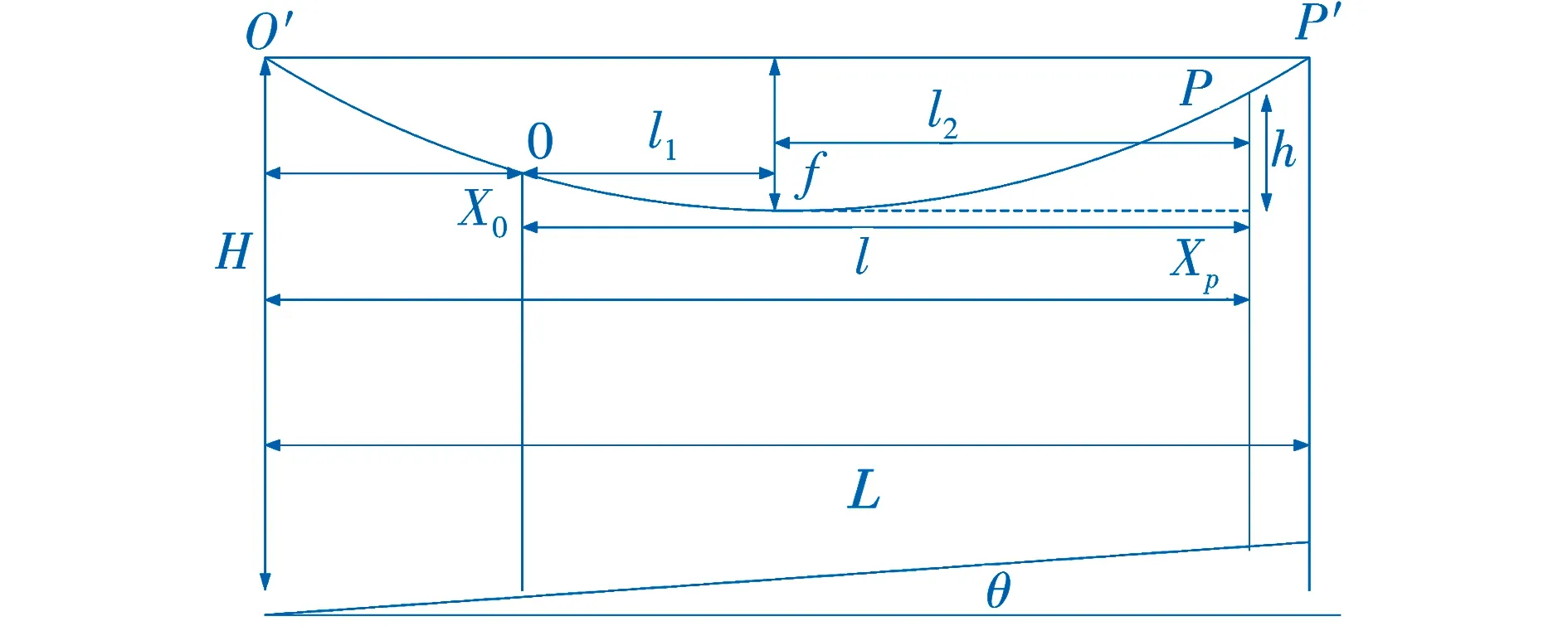
图4 山区地区导地线高度示意图
山区导地线高度示意图,如图4所示。山区绕击三维分析方法是在平原基础上进行改进,图4中O、P两点代表导线或地线悬挂点,θ为地面倾角。由于O、P两点不等高,无法直接运用公式(3),因此将弧AB向两边延伸分别至O′点和P′点,使得O′点与P′点等高,做出代表档距,利用等量关系求出O点与P点坐标,求法如下[10]:
(13)
式中:Xo为O点横坐标;Xp为P点横坐标;hxo为O点对地高度;hxp为P点对地高度。
解得:
这样假设O′点与P′点为避雷线或导线悬挂点,就可仿照平原地区进行计算,只不过在计算总绕击跳闸率时,积分区间为(Xo-Xp),计及山地倾角时,需对一些数据进行如下修正,经推导可得:
lBxyDxy=rccos(θ1+φ)xy-rccos(θ2+φ)xy,
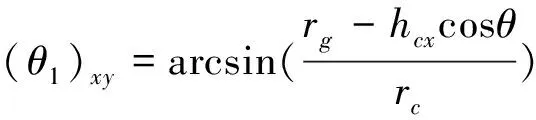
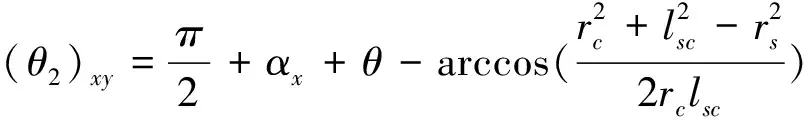
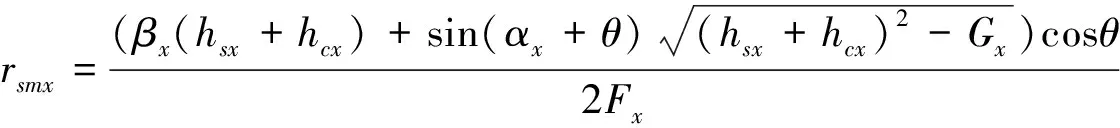
Fx=βx2-sin2(αx+θ);
Gx=Fx((hsx-hcx)/cos(αx)cosθ)2.
总的绕击跳闸率为:
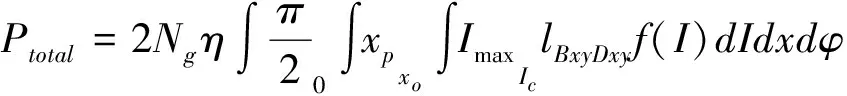
(14)
2.3 大跨越大沟谷地形
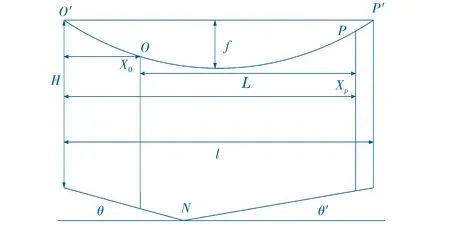
图5 大跨越大沟谷地形导地线高度示意图
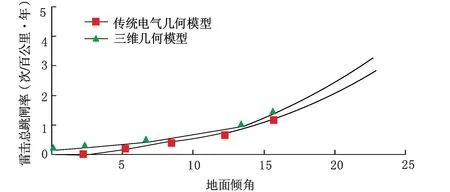
图6 计算结果折线图
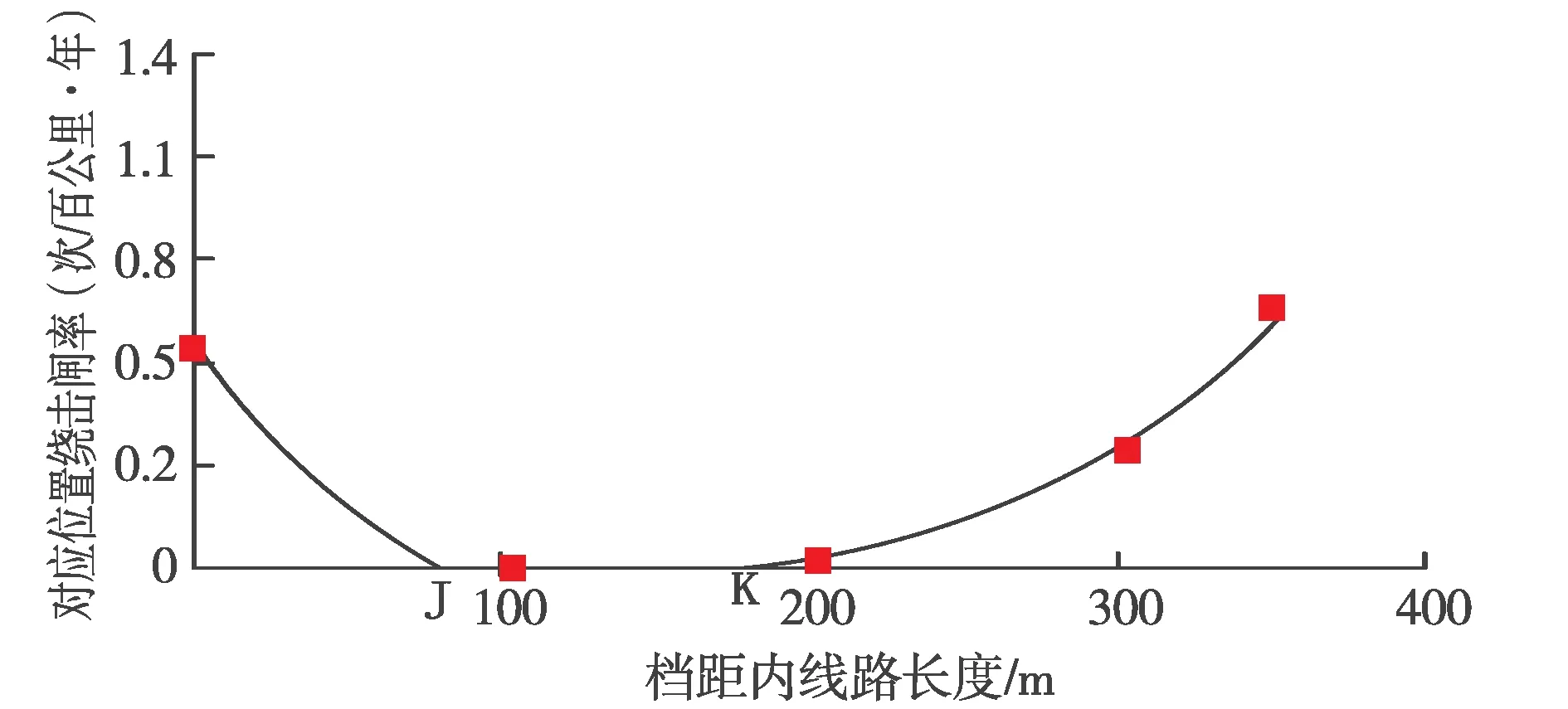
图7 沿档距方向不同位置处绕击跳闸率变化曲线
大跨越大沟谷地形示意图,如图5所示。在图5中,N点为谷底,这种情况在计算绕击跳闸率时,需要在前面所推导的公式上进行修改,由于N点两侧地面倾角不同,所以在积分时需要进行分段,此时绕击跳闸率公式为:

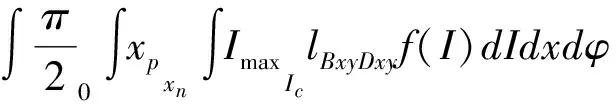
(15)
3 算 例
3.1 算例1
以通化220 kV输电线路长郑线7号杆塔为例:7号杆塔所处地形属于图4中的情况,杆塔型号为ZM3型直线塔,海拔高度为182.8 m,塔高43.5 m,档距363 m,两避雷线间水平距离为9.6 m,导线弧垂17 m,避雷线弧垂12 m,导线与避雷线水平相距2.3 m,8号塔塔高24 m,海拔高度为178.4 m。下面在不同地面倾角情况下,利用传统电气几何模型与本文提出的方法在此档距内进行绕击跳闸率的分析计算,计算结果如图6所示。
由图6可以看出,运用传统电气几何模型计算时,当杆塔处于平原(地面倾角为0)或地面倾角较小时,绕击跳闸率为0,但是运用三维模型计算绕击跳闸率时,杆塔处于平原仍然具有绕击跳闸的风险。为了解释这种现象,现做出沿着档距方向不同位置处的绕击跳闸率,如图7所示。
由图7可见,沿着档距方向JK段绕击跳闸率为0,这是因为JK段距离地面较其他段近的多,大地的屏蔽作用强。运用二维电气几何模型计算时,所取得导地线平均高度正好位于图7中JK段,因此计算结果为0,这只能表示该高度下的绕击跳闸率。运用传统电气几何模型时,导地线高度用的是平均高度,计算出的结果只能表示某一高度处的绕击跳闸率,得到绕击跳闸率只能说明该档距内的平均水平,而沿着档距方向输电线路不同高度处存在某一段线路绕击跳闸率不为0,这种情况在传统电气几何模型中不能够反映出来。本文采用的三维电气几何模型,充分考虑了档距内导地线每一点的对地高度,计算结果能够较为准确的反映真实情况。
3.2 算例2
2014年6月12日16时25分,通化220 kV输电线路长郑线104号杆塔B相跳闸,跳闸原因为雷电绕击。 104号杆塔所处地形属于图5中的情况,图8给出了104号全塔图,图9为104号杆塔大号侧通道。

图8 104号全塔图9 104号大号侧通道
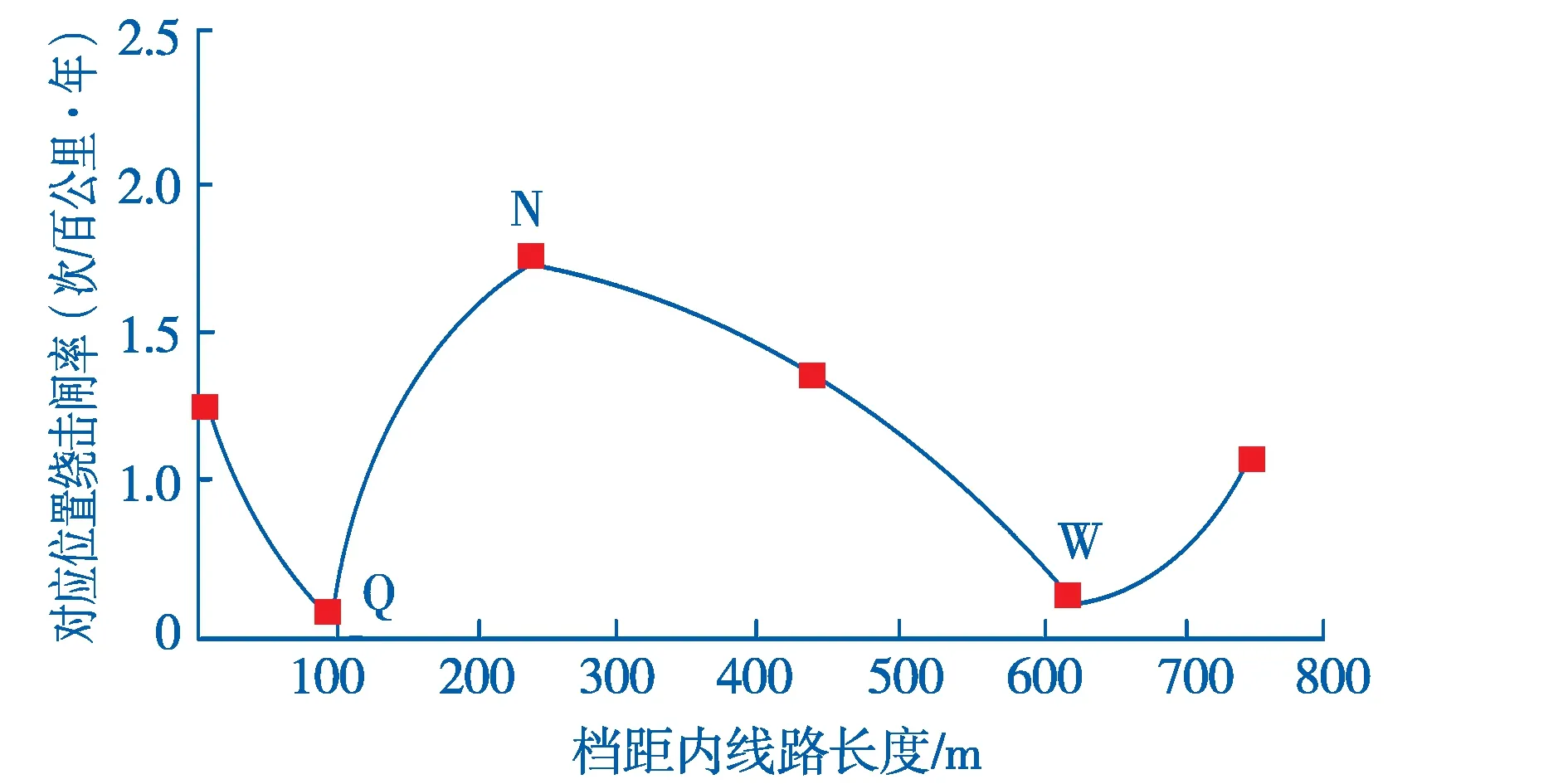
图10 沿档距方向不同位置处绕击跳闸率变化曲线
从图9中可以看出,104号杆塔与105号杆塔档距内地形属于大沟谷类,104号杆塔型号为GJ1型耐张塔,海拔高度为580.1 m,杆塔高度为33 m,线路档距为749 m,避雷线弧垂15 m,导线弧垂20 m,两避雷线间水平距离为9.4 m,导线与避雷线水平相距1.8 m;105号塔海拔高度为628.2 m,杆塔高度为25.5 m,N点为谷底,海拔高度为496m,距离104号塔水平距离为241 m,θ=20°,θ′=25°。二维电气几何模型算得绕击跳闸率P=0.728 5(次/百公里·年),而用本文三维电气几何模型算得绕击跳闸率P=1.566 2(次/百公里·年),相差2.1倍。沿着档距方向不同位置处的绕击跳闸率,如图10所示。
由图10可以看出,沿着档距方向绕击跳闸率波动比较大,其中谷底位置(图中N点)处绕击跳闸率最大。这是因为N点导线距离地面最高,地面对其屏蔽作用最弱,而Q点和W点距离地面较其他点近,受到的大地屏蔽作用强,绕击跳闸率低。因此,仅仅以导地线平均高度来进行计算已经不能够反映线路实际水平。
4 结 论
(1)传统电气几何模型或后来改进的二维电气几何模型,都是以导地线平均高度进行计算的,计算结果只能是以某一高度来代表线路的整体水平,而对于档距较大的输电线路来说,由于沿着档距方向绕击率波动较大,仅以平均高度无法反映线路的实际绕击耐雷水平。
(2)本文对传统二维电气几何模型进行三维拓展,考虑了沿档距方向每一点导地线对地高度,并通过实际案例,将二维电气几何模型与三维几何模型进行对比分析,说明了本文所运用方法更能反映线路的真实绕击跳闸率。
[1] 吴凡.鲁志伟,等.220kV同塔双回线路雷击双回同跳防雷改造[J].东北电力大学学报,2015,35(3):6-11.
[2] 王晓彤,施围,刘文泉.改进电气几何模型计算输电线路绕击率[J].高电压技术,1998,24(1):85-87.
[3] 李晓岚,尹晓根,等.基于电气几何模型的绕击跳闸率的计算[J].高电压技术,2006,32(3):42-44.
[4] Eriksson A J.An improved electro-geometric model for transmission line shielding analysis[J].IEEE Transactions On Power Delivery,1987,29(3):859-870.
[5] T.Udo.Estimation of lightning shielding failures and mid-span back-flashovers based on the performance of EHV double circuit transmission lines[J].IEEE Transactions On Power Delivery,1997,12(2):832-836.
[6] S.Taniguchi,T.Tsuboi,S.Okabe.Observation results of lightning shielding for large-scale transmission lines[J].IEEE Transactions On Dielectrics and electrical insulation,2009,16(2):552-559.
[7] 吕金煌,许宇航,陈钢.输电线路大档距、大转角、大高差杆塔防雷措施的探讨[J].水电能源科学,2010,28(10):135-137.
[8] 周远翔,鲁斌,等.山区复杂地形输电线路绕击跳闸率的研究[J].高电压技术,2007,33(6):45-49.
[9] 李瑞芳,吴广宁,等.输电线路雷电绕击率的三维计算方法[J].电工技术学报,2009,24(10):134-138.
[10] 吴广宁,熊万亮,等.输电线路绕击特性的三维分析方法[J].高电压技术,2013,39(2):374-382.
[11] 司马文霞,郑皓元.复杂地形下输电线路绕击跳闸次数3维计算方法[J].高电压技术,2014,40(3):662-668.
Calculation of Shielding Failure Flash-over Rate of Transmission Line Based on Three-dimensional Electro-geometric Model
Li Bo1,Lu Zhiwei2,Jia Ru2,Song Qingqiu3
(1.Electric Power Research Institute,Eastern Inner Mongolia Electric Power Company Limited,Huhehaote Inner Mongolia 010020;2.Electrical Engineering College,Northeast Electric Power University,Jilin Jilin 132012;3.State Grid Jilin Electric Power Company Limited,Tonghua Electric Power Company,Tonghua Jilin 134001)
As the terrain of mountainous area is complicated,to calculate shielding failure flash-over rate correctly is difficult.Traditional two-dimensional electro-geometric model and the standard method use the average height to calculate,which only reflects the overall level of the line.But it can not represent the actual situation,especially for the large span of the transmission line.The use of the calculation of average height may obtain a smaller conclusion.But in fact the shielding failure flash-over of some section of the line is large.Therefore,the improvement of the method of shielding failure flash-over is necessary.Taking into account the height of each point on the line,the paper improves two-dimensional electro-geometric model.Three-dimensional electro-geometric model is introduced in the paper.At last,two practical examples of 220kV transmission line are utilized to compare three-dimensional electro-geometric model with two-dimensional electro-geometric model.The result is that three-dimensional electro-geometric model is reliable.
Large span;Shielding failure flash-over rate;Two-dimensional electro-geometric model;Three-dimensional ele ctro-geometric model
2017-03-12
2016年吉林省电力有限公司科技项目(SGTYHT/14-JS-188)
李 博(1990-),男,助理工程师,主要研究方向:高电压与绝缘技术.
1005-2992(2017)04-0039-06
TM614
A
电子邮箱: 811756690@qq.com(李博);1443958749@qq.com(鲁志伟);980016810@qq.com(贾茹);13943592950@163.com(宋庆秋)

