不规则波情况下沿岸流不稳定运动传播方向的研究

张雅洁，任春平，2

（1.太原理工大学水利科学与工程学院，山西太原030024；2.天津大学水利工程安全与仿真国家重点实验室，天津300072）

不规则波情况下沿岸流不稳定运动传播方向的研究

张雅洁1，任春平1，2

（1.太原理工大学水利科学与工程学院，山西太原030024；2.天津大学水利工程安全与仿真国家重点实验室，天津300072）

本文以沿岸流不稳定运动实验中流速仪采集到的不规则波的流速时间历程为基础，利用相关性分析，得到两个不同位置处对应流速时间历程的最大相关系数和延迟时间，进而分析沿岸流不稳定运动在1∶40和1∶100平直斜坡上的传播方向，并且分析了其随入射波高、周期的变化。结果表明沿岸流不稳定运动在海岸垂向环流系统的作用下，其传播方向会向海方向偏移，与岸线角度大约在0°到45°之间，且在1∶40和1∶100坡情况下，沿岸流不稳定运动的偏移角分别随入射周期和波高的增加而增加，但1∶100坡的增加幅值较小，大约为1∶40坡情况下的1/2。

沿岸流；不稳定运动；不规则波；相关性分析；传播方向

沿岸流是由波浪破碎引起波生流，与裂流、质量输移流三者构成近岸环流系统，沿岸流不稳定运动伴随时均沿岸流而产生。了解沿岸流以及近岸环流系统的运动规律，尤其是研究其运动方向，对于追溯海岸岸线的演化、研究海岸泥沙污染物的运动扩散运移及海岸水体的交换方面有直接而深刻的意义。一些学者如Russel（1993），Miles（2002），Smith（2002）和Agaard（1994）等分别指出沿岸流不稳定对于海岸侵蚀，沉积物的输运，泥沙运动都有很大关系。之后Sanchez（2003）也表明海岸特殊地形的形成也是沿岸流不稳定运动的杰作。国内研究者薛春汀等（2010）发现在我国东北部海岸，沿岸流在沉积物的空间分布上起了明显的控制作用。

1989年，沿岸流不稳定运动作为一种超低频波波动首次被观测到（Oltman-Shay et al，1989），其波长小于同情况的重力波，且该波动伴随时均沿岸流的出现而出现，大小、方向也会随着时均沿岸流的改变而发生改变。之后，Reniers等（1997）人研究发现沿岸流不稳定运动的产生主要受地形的限制，并且随着入射波高的增大沿岸流作用的强度也会增大。2004年，Noyes等（2004）通过现场实验采集的流速时间历程分析得出沿岸流不稳定主要出现在沿岸流的最大值附近。国内学者邹志利（2005）、金红（2006）在大连理工大学实验室将观测得到沿岸流不稳定运动利用墨水滴入后的运动轨迹形象的展现了沿岸流不稳定的运动变化，使得沿岸流不稳定运动有形而直接的展现出来。

因此，本文研究沿岸流不稳定运动的方向，是岸滩养护、近岸水环境保护直接而重要的参考因素，也给沿海岸的工程实施、管理运作提供了基础理论，对今后海洋排污工程的环境保护措施的提出起到促进作用。

1 实验简介

本文以大连理工大学海岸和近海工程国家重点实验室的沿岸流不稳定实验为基础，利用对流速仪所测得的不同波况下的流速时间历程，分析在沿岸方向不同位置处流速时间历程的相关性，研究沿岸流不稳定运动的传播方向。本文共分析了15个波况，入射波全部为随机波，其中坡度为1∶100地形上的共有6个波况（irregular mild slope,简称im），坡度为1∶40地形上的共有9个波况（irregular steep slope,简称is），详细波况参数见表1。

实验水池长55 m，宽34 m，深1.0 m（见图1），海岸地形为平直斜坡，其坡度分别采用1∶100和1∶40两种（见图2），利用可移动式方向谱造波机造波。平直斜坡海岸坡度均匀，两种坡度情况下均和造波板成30°夹角，目的是使海岸线的长度增加。流速仪32个，垂直岸线布置两列，测量垂直岸线和沿岸方向的速度。从床底算起，流速仪布设于水深的1/3处，图3和图4分别给出了1∶40和1∶100地形上流速仪的布置图。

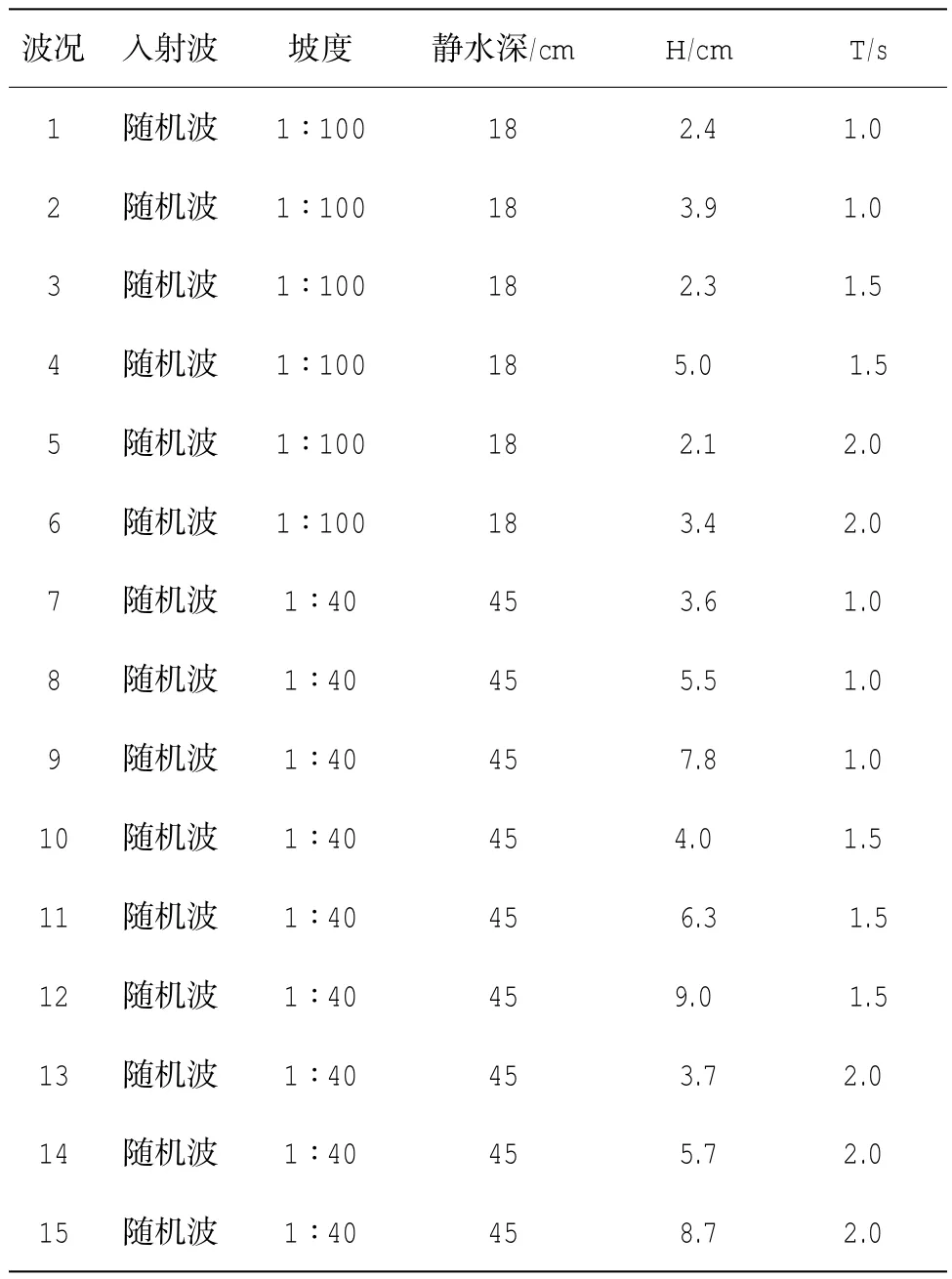
表1 波况参数（对于不规则波：H为平均波高，T为平均周期）

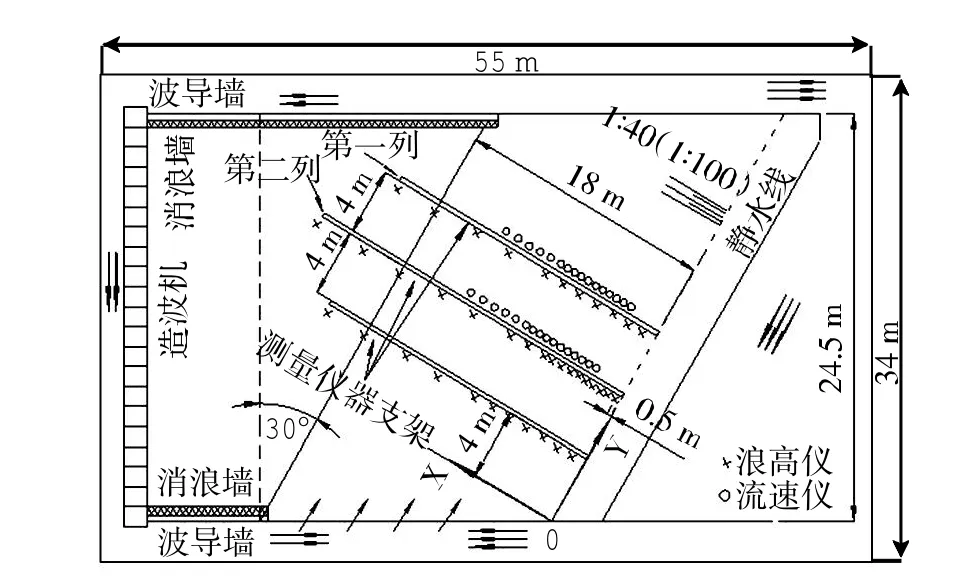
图1 实验布置

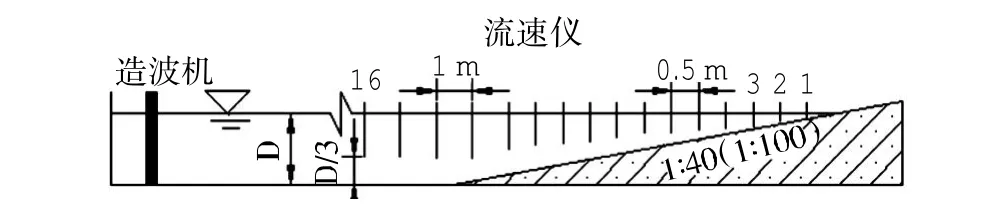
图2 实验地形

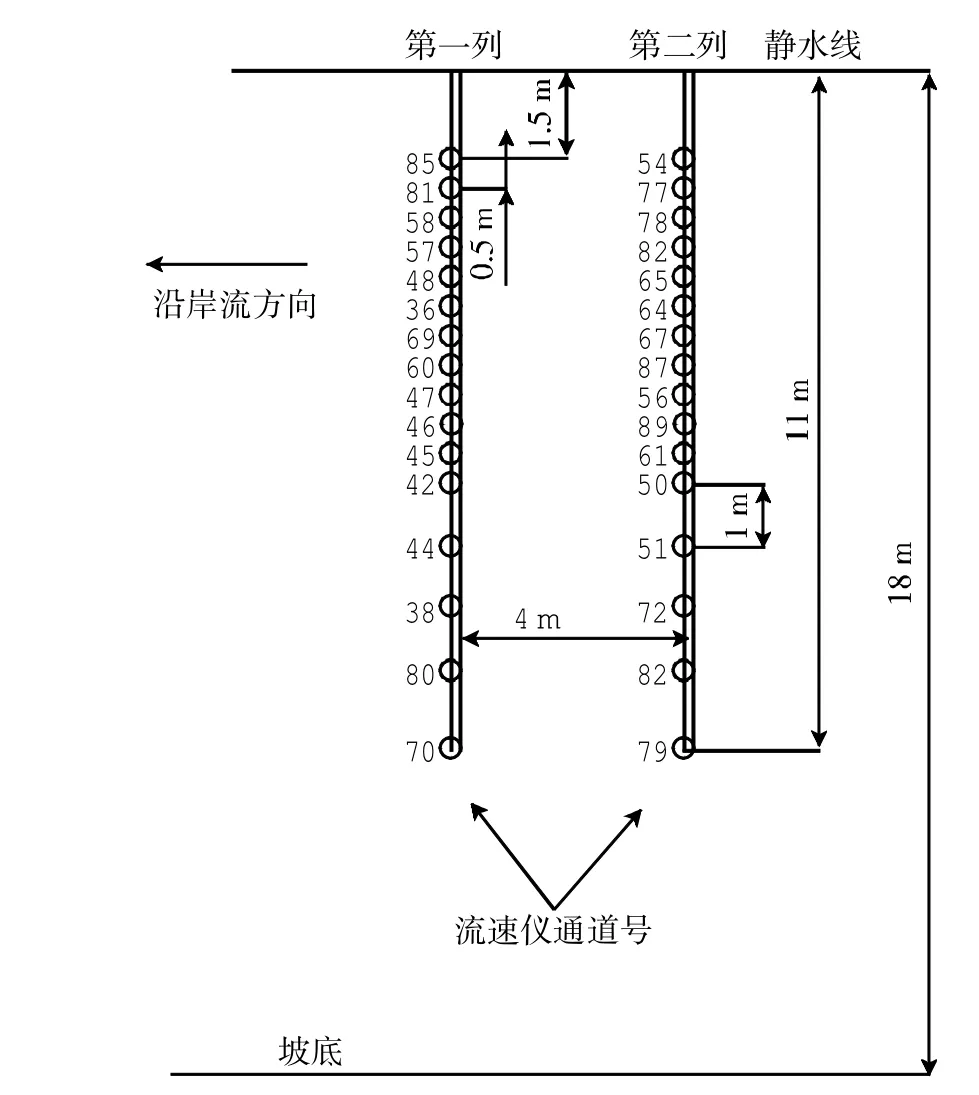
图3 1∶40地形流速仪布置（○为流速仪）

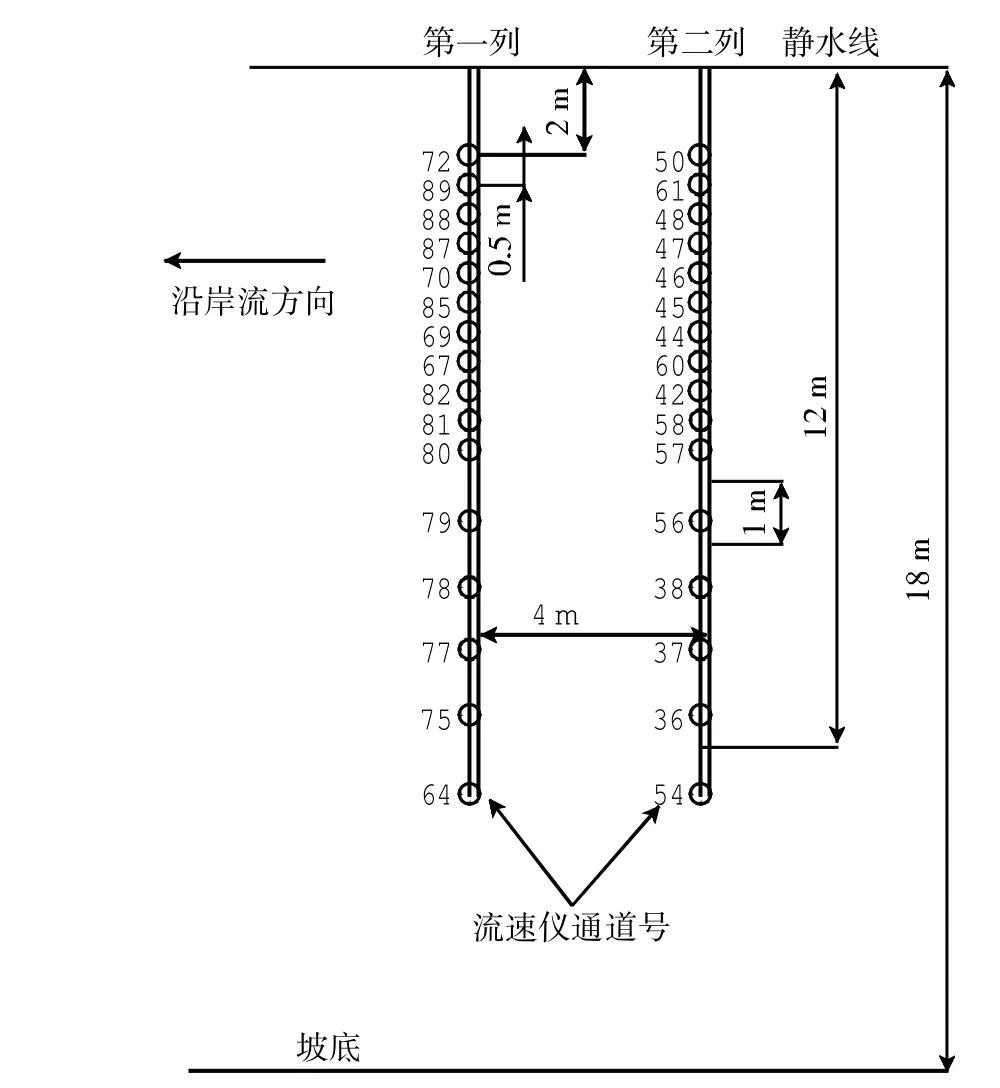
图4 1∶100地形流速仪布置（○为流速仪）

2 沿岸流不稳定运动传播方向分析方法

邹志利（2005），任春平（2009）对沿岸流不稳定运动的实验研究和理论分析，分析并总结出各种波况下垂直岸方向和沿岸方向流速时间历程的特点，如沿岸流不稳定运动的波动周期、幅值，以及传播速度，而本文在此研究的基础上，通过沿岸距离不同的流速仪所测得的流速时间历程，分析不同列的两个流速仪测得的数据，经过滤波（任春平，2009）（双向滤波）来消除高频信号的影响，再利用相关性分析原理，得到两列时间序列的最大相关系数及对应的延迟时间，最终由所得的相关系数和延迟时间进一步分析沿岸流不稳定运动的方向，是将之前的理论研究应用于更加深刻的实践分析。

2.1 相关性分析

相关性是数理统计的经典概念，相关分析也是本文的核心原理。目前，相关性分析广泛应用于数据分析挖掘领域，也有学者提出应用典型相关分析原理并将其用于跨领域的迁移学习方法（张博等，2015）中，反应序列的总体相似性。时间序列多数情况下是一组以数据流的形式出现的数据，并按照发生时间的先后顺序前后排列。如在Gilbert等（2001）对网络数据的快速总结与分析和Chen等（2000）提出的一种可扩展的网络数据库连续查询系统中均有时间序列的应用。因此，分析时间序列的相关性，可以对未来未知的现象做出预测，最常用的衡量标准即互相关函数（S.Thuiner et al，1998）。经典的互相关是用来度量两个信号x（t）和y（t）的相关程度，互相关系数有如下定义：

式中，Cxy=E[x（t）y（t）]，Cxx=E[x（t）2]，Cyy=E[y（t）2]。t为两个信号所取的时间点，假设t1-t2为两个信号的延迟时间，延迟时间是两个时间序列达到某一相关程度时，其所处时间点的时间差，则定义两个时间序列的互相关系数为：

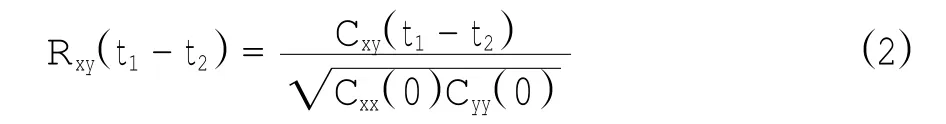
式中，Cxy（t1-t2）=E[x（t1-t2）y（t1-t2）]。式（2）是两个信号进行互相关分析在时域产生时间平移（即发生时间延迟）的相关性度量公式。由于互相关函数反应两个时间序列的相似程度，所以互相关函数取得最大值的地方，即为相关性最大处。而此时所对应的时间差τ=t1-t2即为延迟时间。

实际在处理时间序列相关数据的过程中，延迟时间的选择往往受到阻碍。由于在数据处理前，规定了沿岸流的方向，则以沿岸流方向为正方向，也就规定了流速仪测量的先后，因此在计算两个流速仪的最大相关系数时，延迟时间均取为正。而结果得出的τ-R函数关系图大致为周期不等的正弦函数图，以波况10（1∶40坡，周期为1.5 s，波高为4.0 cm）下第二列x=6 m和x=1.5 m第一列的流速仪的相关系数图为例（见图5），τ>0部分出现两个峰值，而相关系数最大值又处于第二个峰值，但此时的延迟时间又过大，所以就要解决如何确定延迟时间的问题。

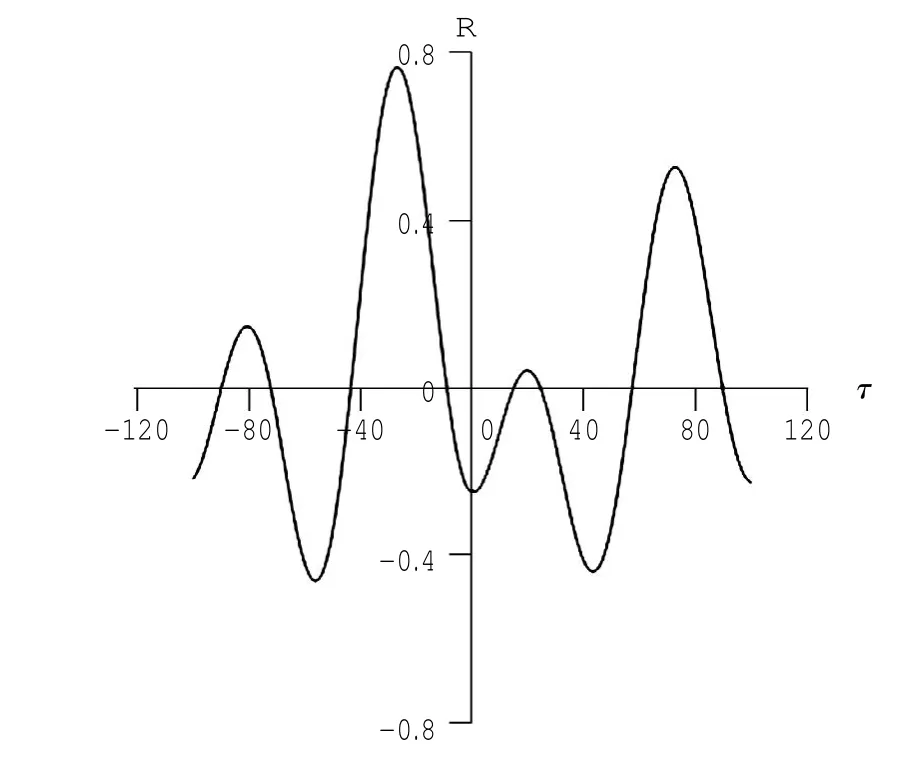
图5 波况τ-R函数关系图

引入延迟（滞后）相关（岳德军，2008）的定义，两个序列x1，y1存在滞后关联，设x1滞后于y1，滞后时间为τ，当：

（1）滞后相关系数R在τ时的绝对值大于相关性阈值γ，阈值，就是使得某种作用效应能够发生的某一条件的临界值（最小值或者最大值），并且R是一个局部最大值点。

（2）如果存在多个局部最大值点，则首个局部最大值点对应的时间为延迟时间。

在上述定义中，条件（1）中的阈值，为延迟时间τ的最小值，由于规定了正方向，所以延迟时间为大于0的正数，所以阈值即为τ=0；条件（2）表明，当两个时间序列有相同的周期T时，则会在时间点（τ，τ+T，τ+2T）上存在多个局部最大值，但我们只选取最早的作为延迟时间，通常情况下首个局部最大值显然是最重要最有价值的。所以图5中的延迟时间应取大约τ=20处的极值。

3.2 分析方法

沿岸流平行沿岸方向流动，沿岸流不稳定运动伴随沿岸流而产生，倘若沿岸流不稳定运动的方向也平行于沿岸，那么对距岸线距离相等的两个异列流速仪所测得的流速时间历程进行相关分析，理应得出相关系数最大，延迟时间最短的结论。如果计算所得的数据符合上述结论，说明沿岸流不稳定运动是平行于沿岸方向传播的，即沿岸流不稳定运动的传播方向平行于沿岸方向。

利用已有的不同波况下流速仪测得的流速时间历程，分别对1∶40和1∶100坡度下不规则波的沿岸流沿岸方向的相关性进行计算，由于流速仪数量多，为提高分析效率，因此选取具有代表性的流速仪处理。在1∶40坡度情况下，两列均取1.5 m，2.0 m，3.0 m，4.0 m，5.0 m，6.0 m，7.0 m，9.0 m，11.0 m处的流速仪两两进行相关性计算；同理，在1∶100坡度情况下，两列均取2.0 m，2.5 m，3.5 m，4.5 m，5.5 m，6.5 m，8.0 m，10.0 m，12.0 m处的流速仪两两进行相关性计算。分别于15种波况下进行分析，列表记录所得的最终数据结果（相关系数和延迟时间），制出散点图，观察规律，分析其在沿岸方向（x方向）的相关性。

3 实验结果分析

实际沿岸流多为不规则波，则结合实际情况，本文将不规则陡坡情况下的波况都做了相关分析，得出的一系列数据进行观察比较，发现与之前的假设并不相符。下图给出了不同波况下第二列流速仪通过与第一列流速仪逐个进行相关性比较分析，最终得到相关系数最大的两个流速仪对应的相关系数和延迟时间，并以两个流速仪中位于第二列的流速仪所对应的垂直于沿岸的距离为x轴，得到相关系数与延迟时间分别随沿岸距离的变化情况（R表示相关系数，x表示流速仪距离岸线的距离，τ表示延迟时间）,由于波况太多且受篇幅限制，仅抽取具有代表性的波况，对于1∶100坡情况下，选取波况1、3、5进行分析比较（波况1、3、5的波高相近，周期逐个增加）；对于1∶40坡情况下，选取7、9、10、12、13、15六组进行分析比较（其中7、9，10、12，13、15三组分别为周期相同，波高逐个增大；7、10、13，9、12、15两组分别为波高相近，周期逐个增加），见图6，图7。观察发现，并不是每个流速仪都与其距沿岸距离相同的异列流速仪进行相关分析时得出的相关系数最大，延迟时间为最小，也就是剪切波的传播速度（流速仪间隔与延迟时间的比值）最大，这表明沿岸流不稳定运动的传播方向并非平行于沿岸方向。

假设沿岸流不稳定运动的传播方向平行于沿岸，在根据不同波况下，将第一列流速仪分别与第二列流速仪进行相关性分析，找出每种波况下沿岸距离相同的两个异列流速仪，按照沿岸距离由小到大排列。观察发现，在1∶40坡情况下，相关系数R峰值在波况7、9分别出现在x=4 m、x=4 m处；在波况10、12出现在x=3 m、x=4 m处；在波况13、15则出现在x=1.5 m、x=3 m处；而1∶100坡情况下波况1、3、5则分别出现在x=6.5 m、x=5.5 m、x=3.5 m处。在这两种坡度下，R的峰值所对应的延迟时间也相对较小。这说明剪切波在R达到峰值处传播的速度较大，相关性最大，沿岸流不稳定运动在此处较显著，而在两种坡度下R峰值所处的距离沿岸的位置不同，说明坡度对沿岸流不稳定运动有一定影响。总结两种坡度的规律，发现在波高相近的情况下，随着入射波周期的增加，相关系数R的最大值也增加，同时峰值距离沿岸的距离在减小；而在相同入射周期情况下，随着波高的增加，R的最大值同样也增加，而峰值距离沿岸的距离却增加。这说明入射周期T和波高H均对沿岸流不稳定运动有影响。

对比1∶100和1∶40的整体情况，1∶100的最大相关系数整体都较1∶40的小，说明在1∶100情况下，两列流速仪在沿岸方向相关程度低，也就是说沿岸流不稳定在1∶100情况下较弱。

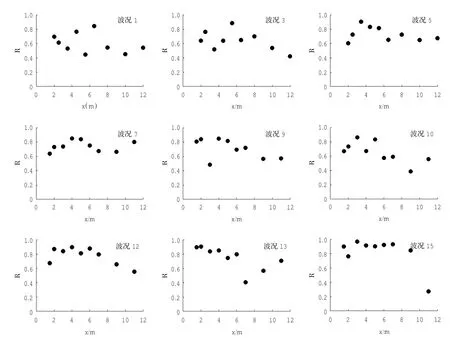
图6 选取的具有代表性的各个波况下最大相关系数随沿岸距离变化图

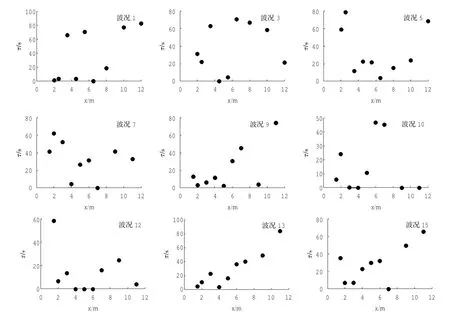
图7 选取具有代表性的各个波况下最大相关系数所相应的延迟时间随沿岸距离变化图

根据Noyes等（2004）由流速时间历程所得出的结论，即沿岸流不稳定主要出现在沿岸流的最大值附近，应用于沿岸流不稳定运动的方向的研究，取上述相关性最大处（沿岸流不稳定作用最大）进行分析。找到每种波况下，两列流速仪中R峰值处对应的两个流速仪，其中位于第二列的流速仪所在位置为x1，位于第一列的流速仪所在位置为x2或x3，二者的距离差Δx与两列流速仪的间隔差L的比值，即可求出沿岸流不稳定的偏移角α。定义以相关系数最大的两个流速仪的连线为一边，平行于沿岸方向且与位于第二列的流速仪相交的直线为另一边，则两直线的夹角即为偏移角α，示意图见图8。详细数据见表2，表3。

举例说明计算沿岸流不稳定运动的偏移角，两列流速仪间隔L=4 m，例如波况6，偏移角tan（α1）=（x2-x1）/L=（4-2.5）/4=0.375，α1=arctan（0.375）=20.56°由上表可以看出1∶100坡沿岸流不稳定向海方向偏移不超过20.56°，发现在波高相近的情况下，随着入射波周期的增加，偏移角也增加；在入射周期相同的情况下，随着波高的增加，偏移角也在增加。说明在1∶100坡情况下，入射周期和波高对沿岸流不稳定运动的偏移角均有影响。

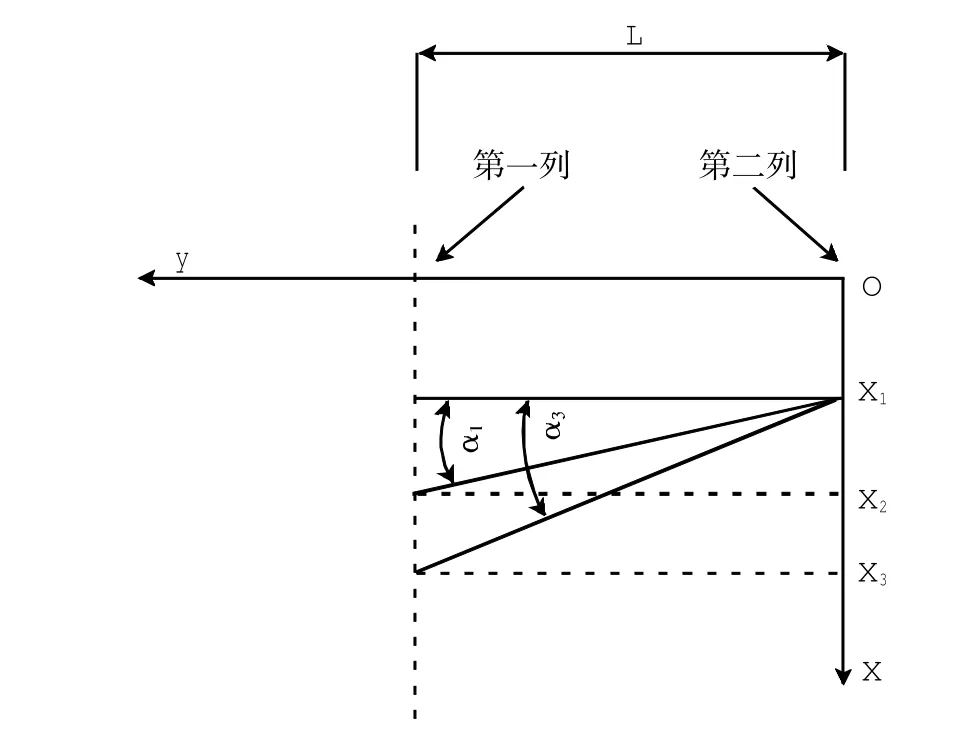
图8 求解偏移角α示意图

举例说明计算沿岸流不稳定运动的偏移角，两列流速仪间隔，例如波况9，偏移角度tan（α1）=（x2-x1）/L=（3-2）/4=0.25，α1=arctan（0.25）=14.04°；再例如波况14，tan（α2）=（x3-x1）/L=（7-3）/ 4=1，α2=arctan（1）=45°。从1∶40坡整体可以看出，沿岸流不稳定向海的偏移方向要比1∶100偏大一倍左右。同样，由上表可以看出，沿岸流不稳定运动的偏移角于1∶40坡在入射周期相同的情况下，随入射波高的增加而增加；在波高相近的情况下，随入射周期的增加也会增加。说明在1∶40坡情况下，入射周期和波高对沿岸流不稳定运动的偏移角均有影响，且影响大于1∶100坡。

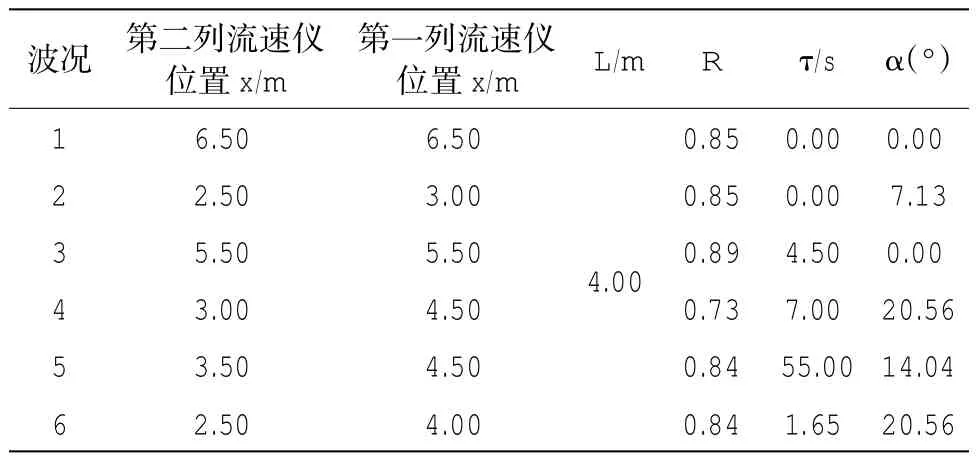
表2 1∶100坡各个波况下沿岸流不稳定运动的偏移角

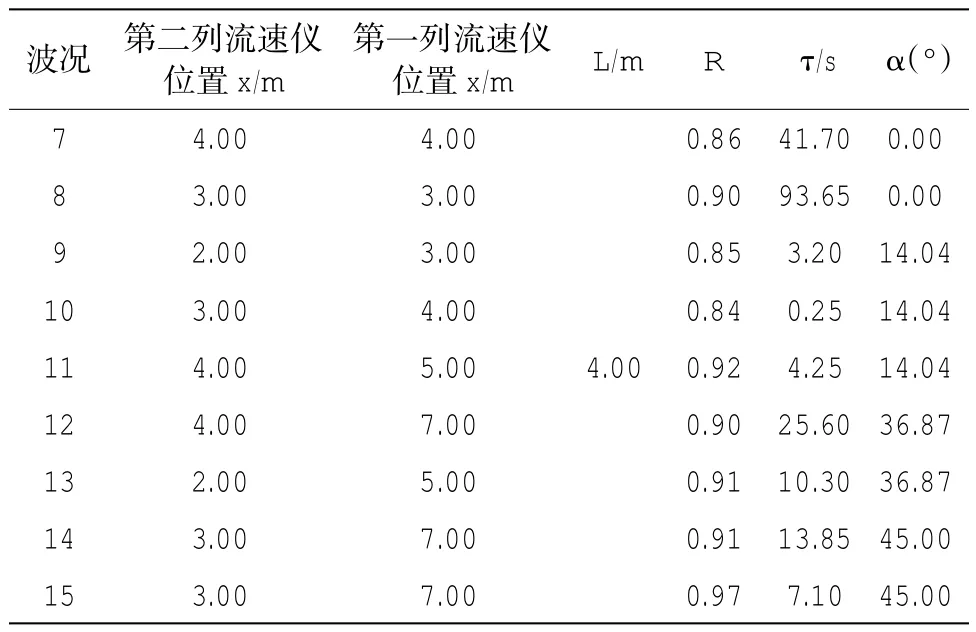
表3 1∶40坡各个波况下沿岸流不稳定运动的偏移角

之所以沿岸流不稳定运动在平直斜坡上会向离岸方向偏移，可能主要是受海底回流的影响，由于本文实验是平直斜坡，海底回流几乎垂直于岸线并向离岸方向运动，与破波带内产生的沿岸流不稳定运动大概成垂直关系。一般来说，沿岸流不稳定运动的强度在时均沿岸流最大值附近最大，而海底回流到达时均沿岸流最大值附近（或破波点附近）时，其强度也达到一定量值，足以使不稳定运动的传播方向产生偏移。更重要的是沿岸流不稳定运动在水深方向（Zhao et al，2003）有比较明显的变化，可以肯定的是其水深方向最大值距离水体表面有一定距离，而海底回流也是在床底部附近，所以海底回流对不稳定运动的作用会更加有效。这样在它的作用下，可能会使不稳定运动稍向海方向偏移。

尽管有质量输移流存在，但是其对于床底部附近的作用要弱很多，可能其对表面附近的作用会强一些，比如对表面物质输移的影响会更明显一些。

4 结语

通过上述分析，得出下述结论：（1）实验中观测到的沿岸流不稳定运动在入射波为不规则波情况下，在1∶40坡向离岸方向偏移不超过45°，在1∶100坡向离岸方向偏移不超过20.56°，说明偏移角的大小受坡度的影响较大。（2）坡度的不同，沿岸流不稳定运动的偏移角所受的影响因素的大小也不同。从1∶40坡整体情况可以看出，沿岸流不稳定运动的偏移角在入射周期相同的情况下，随入射波高的增加而增加的幅度较大；在波高相同的情况下，随入射周期的增加而增加的幅度也较大。说明在1∶40坡情况下，入射周期和波高对沿岸流不稳定运动的偏移角的影响较1∶100大。在1∶100坡情况下，沿岸流不稳定运动的偏移角受入射波周期和波高的影响幅度较小，偏移角的大小只有1∶40坡度下的1/2左右。无论在哪种坡度，沿岸流不稳定运动的偏移角均未超过45°，本文所建立的实验研究基础上，可以认为45°为沿岸流不稳定运动方向偏移的临界值。（3）在实际情况下，由于垂向环流系统的影响，沿岸流不稳定运动运动方向并非平行海岸，而是向海方向偏移，并且床底部受海底回流的作用更加有效，而质量输移流则对其表面附近的作用稍强。

在实际运用当中，海岸泥沙和污染物在近岸环流系统中的的输移方向也会随沿岸流偏向向海方向，这样就会有泥沙浓度（周鸿权等，2014）的变化，因此在采取治理和保护措施的时候，参考其运动方向，进一步设置阻挡物或相应措施，这样在有效的理论基础上才会起到更好的环境保护作用。沿岸流不稳定运动偏向向海方向，对是否加快了环流系统循环速度（汪求顺等，2015），提供了理论科学依据，从而提高水体交换能力，改善自净能力，最终做到更加合理的海岸规划。

致谢：师兄季海嘉为文章修改提供帮助。

参考文献

Aagaard T,Greenwood B,1994.Suspended sediment transport and the role of infragravity waves in a barred surf zone.Marine geology, 118:23-48.

Chen J,DwWitt D,Tian F,et al,2000.NiagaraCQ:A Scalable Continuous Query System for Internet Databases.In Proc.of ACM Int'l Conf.on Management of Data,379-390.

Gilbert A C,Kotidis Y,Muthukrishnan S,et al,2001.QuickSAND:Quick Summary and Analysis of Network Data,DIMACSTechnical Report, 43.

Holman R A,1983.The CRC Handbook of Coastal Processes and Erosion. Boca Raton:CRC Press.

Miles J R,Russell P E,Ruessink B G et al,2002.Field observations of the effect of shear waves on sediment suspension and transport. Continental Shelf Research,22(4):657-681.

Noyes T J,Guza R T,Elgar S et al,2004.Field observations of shear waves in the surf zone.Journal of Geophysical Research,109(C0): 1031,doi:10.1029/2002JC001761.

Oltman-Shay J,Howd P A,Birkemeier W A,1989.Shear instabilities of the mean longshorecurrent 2.field observations.Journal of Geophysical Research,94(C12):18031-18042.

Reniers A,Battjes J A,Falques A,et al,1997.A laboratory study on the shear instability of longshore currents.Journal of Geophysical Research,102(C4):8597-8609.

Russell P E,1993.Mechanisms for beach erosion during storms. Continental shelf research,13(11):1243-1265.

Sanchez M O,Losada M A,Baquerizo A,2003.On the development of large-scale cuspate features on a semi-reflective beach:Carchuna beach,Southern Spain.Marine geology,198:209-223.

Smith G G,Mocke G P,2002.Interaction between breaking/broken waves and infragravity-scale phenomena to control sediment suspension transport in the surf zone.Marine Geology,187:329-345.

Thuiner S,Feurstein M,Teich M,1998.Multiresolution Wavelet Analysis of Heartbeat Intervals Discriminates Healthy Patients from Those with Cardiac Pathology.Phys.Rev.Lett,80:1544-1547.

Zhao Q,Svendsen I A,Haas K,2003.Three-dimensional effects in shear waves.Journal of Geophysical Research:Oceans(1978-2012),108 (C8).

金红，邹志利，邱大洪，等，2006.波生流对海岸污染物输移的影响.海洋学报(中文版)，28（6）：144-150.

任春平，2009.沿岸流不稳定运动的实验研究及理论分析.大连理工大学.

汪求顺，康海贵，王科，等，2015.近岸岛屿周围波生流的数值模拟.海洋通报，（4）：450-456.

薛春汀，张勇，2010.中国近海岸区沿岸流和海岸流对沉积物的搬运.海洋地质与第四纪地质，（1）：1-7.

岳德君，2008.时间序列数据流中相关性分析技术的研究.东北大学.

张博，史忠植，赵晓非，等，2015.一种基于跨领域典型相关性分析的迁移学习方法.计算机学报，（7）：1326-1336.

周鸿权，孙昭晨，李伯根，等，2014.浙江象山港海域悬沙浓度分布变化及其水动力影响分析.海洋通报，（6）：694-702.

邹志利，任春平，金红，等，2005.沿岸流不稳定性运动实验研究.第十二届中国海岸工程学术讨论会，334-338.

（本文编辑：袁泽轶）

A study on the propagation direction of the unstable motion of longshore currents under the irregular waves

ZHANG Ya-jie1,REN Chun-ping1,2
（1.College of Water Resource Science and Engineering,TaiyuanUniversity of Technology,Taiyuan 030024,China; 2.State KeyLaboratoryof Hydraulic Engineering SimulationandSafety,TianjinUniversity,Tianjin 300072,China）

Based on the time history of flow velocity of the irregular waves gathered from current meters in the experiment of the instability of longshore currents and using correlation analysis,the max correlation coefficients and delayed time of two different positions were gained in this article,and then the direction of propagation was analyzed in two kinds of flat slopes which had the slope of 1∶40 and 1∶100 of the instability of longshore currents,and its change along with the change of incident wave height and period was analyzed.The results showed that the propagation direction of the instability of longshore currents had a shifting to the sea direction under the vertical coastal circulation system,with the angle of about 0°to 45°.And in the cases of 1∶40 and 1∶40 slopes,the deviation angle of the unstable motion of longshore currents will increase respectively with the increasing of incident period and wave height;and in the 1∶100 slope,the increase amplitude of the deviation angle of the unstable motion of longshore currents is smaller,about half of that in the 1∶40 slope.

longshore currents;the unstable motion;the irregular waves;correlation analysis;propagation direction

P731.21

A

1001-6932（2017）04-0408-08

10.11840/j.issn.1001-6392.2017.04.007

2016-01-14；

2016-04-13

水利工程安全与仿真国家重点实验室开放基金（HESS-1406）；中国博士后基金（2013M541179）。

张雅洁（1991-），硕士研究生，主要从事海岸水动力学研究。电子邮箱：m18536666126@163.com。

任春平，博士，副教授，从事河口、海岸水动力学研究。电子邮箱：chunpingren@163.com。