波浪场中浓度输移扩散Stokes漂移效应的欧拉描述

闫圣，邹志利

（大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

波浪场中浓度输移扩散Stokes漂移效应的欧拉描述

闫圣，邹志利

（大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

为了说明波浪场中浓度输移扩散Stokes漂移效应的欧拉描述方法，采用欧拉方法推导了波浪场中波浪周期平均的浓度输移扩散方程，其对流项是由波浪速度的波动和物质浓度的波动相互作用而产生，所含的对流速度恰是Stokes漂移速度。由此说明，波浪场中浓度扩散问题的Stokes漂移效应可以自动的由欧拉法来考虑，所得到的Stokes漂移效应与拉格朗日描述的结果是等价的。为了进一步说明这一问题，将粒子追踪法的拉格朗日描述的Stokes漂移速度与欧拉法的结果进行了对比，二者是一致的。研究中也数值求解了线性波浪场中σ坐标下浓度扩散方程，将浓度的Stokes漂移、浓度分布和粒子追踪法的结果进行了对比，以证明欧拉描述和拉格朗日描述两种方法的等价性。研究中也根据实验结果对实际波浪场中Stokes漂移效应所引起的浓度漂移进行了讨论，解释了物理模型实验中的观察到的波浪场中浓度漂移现象。

Stokes漂移速度；浓度输移扩散；线性波浪；Taylor离散系数；欧拉法

Stokes漂移是波浪中流体质点在波浪传播方向上的净移动（Stokes，1847），Stokes漂移速度虽不能直接由定点处的流速仪测得，在以往的关于物质输移扩散的数值模型中也很少考虑波浪的影响，但它对海洋中的物质输移扩散和海岸地形演变有着重要的作用。例如，Monismith等（2004）观察到海面波浪较大时沿岸颜料羽流存在向岸偏移，并且这一现象可通过Stokes漂移的影响来解释。他们建议在预报近海物质输运的时间平均方程中应显式地考虑Stokes漂移的影响。Rohrs等（2014）研究表明波浪引起的向岸漂移会影响海岸水域产卵地初次摄食的仔鱼向海洄游，进而使它们的停留时间增加。Henderson等（2004）的研究表明Stokes漂移会引起海岸悬移质泥沙向岸输移进而可引起沙坝向岸移动。本文将讨论Stokes漂移的欧拉描述与拉格朗日描述的一致性，以探讨在欧拉描述的浓度扩散方程中如何考虑Stokes漂移的影响。用欧拉方法阐述了仅以一阶的波浪速度作为背景流场速度就可以产生物质平均浓度Stokes漂移效应的原理，并给出了以Stokes漂移速度作为对流速度的平均浓度扩散方程。

Law（2000）在研究由自由表面波中污染物的Taylor离散（Taylor，1953）时，假设物质颗粒随水质点同相位同幅度运动，它们沿水深变化的时间平均速度剖面就取为Stokes漂移速度剖面，利用Van den Broeck（1990）推导的公式计算得到了Taylor离散系数，然后又采用随机游走的方法来模拟污染物粒子在波浪中的运动，在求解粒子的位置时每一步的位移用粒子瞬时的拉格朗日速度时间积分得到，所以隐含了Stokes漂移速度的影响。以上两种方法得到的离散系数的结果接近，表明两种描述污染物在波浪中扩散的Stokes漂移效应的方法等效。

以上的研究对Stokes漂移流的处理其实是拉格朗日描述，与此对应的也可采用欧拉描述，即在波浪流场中建立扩散物质浓度的控制方程，即浓度对流扩散方程。在理论分析方面，Shen等（2014）把垂向二维污染物浓度扩散方程中的对流速度取为Stokes漂移速度和线性波浪场的速度之和，用连续近似的方法推导了波浪引起的Taylor离散系数，其结果中时间平均的离散系数比Law（2000）的结果大35%。Winckler等（2014）在忽略垂向速度的情况下，推导了在破波带内的水深平均的二维污染物浓度输移扩散方程。他们的理论显示除了波浪破碎引起的沿岸流，由波浪和物质浓度波动的相互作用引起的质量输移是破波带内另一种对流输运，它会引起浓度存在向岸漂移。

数值模拟方面，袁徳奎等（2004）建立了基于σ坐标的浓度对流扩散数学模型，通过数值模拟结果计算波浪场中Taylor离散系数。方程中的对流速度取为解析的线性的波浪速度。经和Law（2000）的结果比较，得出在忽略垂向速度的情况下，用该数学模型计算得到的离散系数与Law（2000）的结果是基本一致的，但在考虑垂向速度后，数值模拟得到的离散系数大于不考虑垂向速度的结果。但他在用解析解布置波浪场时将垂向速度设置为零，这样来忽略垂向速度的影响是不对的，因为此时速度场的散度不为零，即流体质量是不守恒的，这和实际不符，故上面得出的结论也是不可信的，而本文将重审这一方法。

实验研究中，Patil等（2007）等用实验结果和尺度分析得到包含波浪波高和周期参数的波浪和流共同作用下的Taylor离散系数的经验公式，并得出波浪中流体质点漂移速度的存在会增大Taylor离散系数的值。金红等（2006）通过物理模型实验对海岸波浪作用下污染物运动特性进行了观察，实验表明，在破碎带外污染物主要受波浪引起的质量输移流即Stokes漂移流的影响，在破碎带内主要受沿岸流的影响，同时还受沿岸流不稳定运动及大尺度旋涡运动的影响。

本文首先采用解析方法给出了欧拉描述的波浪中物质浓度输移的Stokes漂移效应和Taylor离散，以此分析为基础和上述以往研究工作中拉格朗日方法的结果加以比较。本文研究也采用粒子追踪法和σ坐标下的浓度输移扩散方程对以上问题进行了数值模拟来显示波浪场中浓度输移扩散过程。最后给出了上述的欧拉方法在解释物理模型实验现象中的应用。

1 Stokes漂移影响的欧拉描述

本节将给出欧拉描述情况下波浪场中物质输移的Stokes漂移产生机制，这一方法与上述拉格朗日描述不同之处是：速度场仅考虑欧拉形式的波浪速度，即固定点处的波浪速度，其不含Stokes漂移速度；而拉格朗日描述需要加入Stokes漂移速度。针对波浪场中浓度扩散方程，采用多尺度分析（Mei et al，1997），得到在波浪周期上时间平均的浓度输移扩散方程。

假设输移扩散过程中没有化学作用发生（过程是保守的）并且物质的密度和周围的流体密度相同，则波浪场中浓度满足如下的方程：

式中，x和u代表水平坐标和流体水平速度分量，z和w代表垂直坐标和流体垂直速度分量；Dx和Dz是湍流扩散系数，并假设它们是常量。在自由表面和不可渗透的海底浓度c（x，z，t）满足无通量边界条件。

这里考虑物质浓度在线性波浪中的扩散，即u和w取一阶波浪场的速度

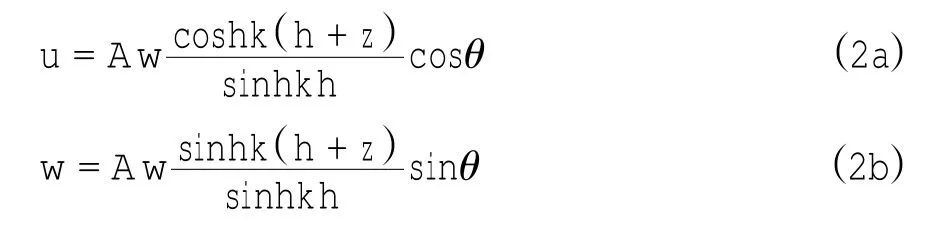
式中θ=kx-wt，A、k、w为波浪的波幅、波数和圆频率，h为水深。

根据破波带外的波浪和物质输移扩散特征，引入下面的无量纲数，

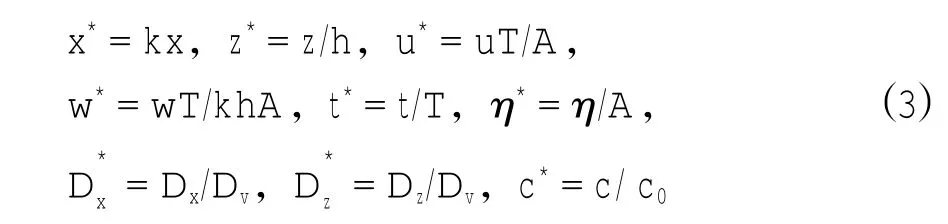
对控制方程（1）进行无因次化，则方程（1）变为

式中，ε=kA为正比于波陡的小参数，T为波浪周期。考虑到物质在波浪中扩散时有两个不同的时间尺度：一是物质浓度随波浪运动的快变时间尺度，对应的快变时间为t；另一个是Stokes漂移效应和扩散引起的慢变时间尺度，对应的慢变时间τ为τ=ε2t。这样，某一点处的物质浓度将是由Stokes漂移和湍流扩散引起的缓慢变化叠加上以波浪周期变化的快变波动。因此，可将浓度按小参数展开为（以下式（5）和式（6）略写无因次量的上标*）

式中，c(0)=c(0)（x，z，τ）为缓慢变化的浓度，c(1)=c(1)（x，z，t，τ）为以波浪周期波动的浓度，c(2)=c(2)（x，z，t，τ）为以二倍波浪周期波动的浓度。将以上展开代入方程（4），采用以下转换

并注意到方程中系数的量级可估计为：kh= O（1），（考虑有限水深的情况）；TDv/h2=O（ε2）（湍流扩散系数Dv很小，波浪周期T和物质扩散时间h2/Dv之比是个小量，这里假定其量阶为ε2。例如，对如下情况：h=3 m，H=0.6 m，T=5s，Dv=0.005 m2/s，则有kh=0.252×3=0.75~O（1），TDv/h2=5×0.005/32=0.002 778，并且ε2=（kA）2=（0.252×0.3）2=0.005 715，即O（TDv/h2）~ε2），则可将方程（4）分解为以下各阶方程，并写成有量纲形式，有O（ε）阶方程

方程（7）表达的是波浪水平速度u和垂向速度w产生的浓度对流，即产生了浓度随波浪周期变化的部分c(1)。因为波浪速度为已知的解析表达式（式（2）），所以该方程解可直接求出，表达式为

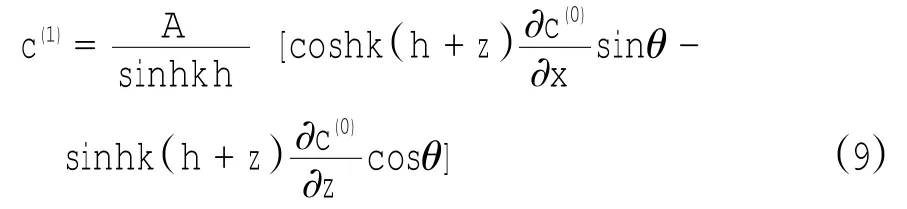
方程（8）表达的是包含ε2阶物理量的动力平衡，实际上方程右端可分解为慢变项和以二倍周期波动的高频项（由u∂c(1)/∂x+w∂c(1)/∂z项中u、w与c(1)的导数的乘积产生，因c(1)也是按波浪周期波动的，见式（9））：前两项仅包含慢变部分，而后两项既包含慢变部分又包含高频部分。方程左端项仅含高频波动项。方程中慢变部分可以通过将方程在周期上做时间平均而将其从方程中分离出来，并恢复t变量，即有

MRI、CT等影像学检查方法均有助于早期诊断隐匿性骨折。螺旋CT扫描轨呈螺旋状前进，扫描时间快，可以不间断地快速采集数据，图像减少了运动伪迹，可以重建出高质量的三维图像。在单层螺旋CT的基础上，又发展起来多层螺旋CT。多层螺旋CT可以同时采集多层投影数据，扫描覆盖范围更大，扫描时间缩短，Z轴分辨率更高。磁共振成像(MRI)是利用外磁场和物体的相互作用来成像，其成像过程与图像重建和CT相近。与CT比较，MRI的主要优点是：（1）对人体无放射性和生物学损害。（2）可以直接生成横断面、矢状面、冠状面及各种斜面的体层图像。（3）不会产生伪影。（4）较CT的显示范围更广泛，结构更清楚。

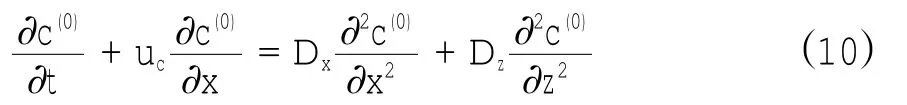
式中uc项来源于方程（8）中波浪速度u和w与以波浪周期波动的浓度c(1)的相互作用，将u、w与c(1)的表达式（2）和（9）代入u∂c(1)/∂x+w∂c(1)/∂z，可得

式中uc为

该表达式与Stokes漂移速度us的表达式（14）相同。后者是由拉格朗日描述（跟踪波浪水质点）来给出的（Longuet-Higgins，1953），即

二者结果一致，但对应的物理过程是有差别的：拉格朗日描述式（15）表达的是波浪水质点位移

所引起的偏移速度时间平均值；而欧拉描述（13）表达的是波浪速度u和w与一阶浓度c(1)= X∂c(0)/∂x+Z∂c(0)/∂z的相互作用。

由于式（12）的推导中的流场是固定点处的波浪速度，而没有另外添加Stokes漂移速度，所以，该推导是欧拉描述的方法，这是本文研究与以往研究（Law，2000）不同之处，后者是用粒子的拉格朗日速度（包含Stokes漂移速度）来研究粒子在波浪中的Stokes漂移。这两种方法得到的结果一致意味着在波浪周期平均下这两种方法对于浓度输移是等价的，也意味着可以直接采用欧拉描述来考虑波浪场中浓度输移扩散的Stokes漂移效应。

在方程（10）中uc的作用相当于相同速度的水流的对流作用，即引起浓度c(0)沿速度方向产生漂移，除此之外uc还将产生离散效应，这一效应是通过将方程（10）沿水深积分体现出来的（Fischer，1979）。沿水深积分后的方程成为

C和U分别是水深平均的浓度和Stokes漂移速度，K是速度uc沿水深分布不均匀产生的离散系数，该表达式中c^(0)和u^c分别是c(0)和uc相对它们自身水深平均值的偏离值，该结果与以往用拉格朗日方法研究所得到的Stokes漂移产生的离散系数是一致的（见Law，2000式（11））。

以下两节将分别给出粒子追踪法的拉格朗日描述结果和直接数值求解浓度扩散方程（1）的欧拉描述结果，并通过两结果的对比来进一步说明上述Stokes漂移速度的欧拉描述和拉格朗日描述的等价性。

2 粒子追踪法模拟波浪场中浓度输移

粒子追踪法的原理是通过计算出流场中物质粒子的运动轨迹来确定浓度分布，因为其是跟踪物质粒子，所以是拉格朗日方法。在这一方法中Stokes漂移是通过粒子的平均位移体现出来的。粒子追踪法（Wolk，2003）所采用的方程为

下面给出一个由粒子追踪法模拟波浪场（式（2））中浓度扩散的例子，以显示在拉格朗日描述中Stokes漂移现象是如何实现的。计算中取水深h=3 m、波高H=0.6 m、波浪周期T=5 s，Dx= Dz=0.005 m2/s。在流场中布置2 000个粒子，粒子初始时刻水平坐标为0，垂直坐标沿水深随机均匀分布，取时间步长0.25 s，根据方程（18）计算粒子任意时间的空间位置。方程右端第一项采用四阶龙格-库塔法进行时间积分，第二项采用随机行走方法处理。若粒子由于随机跳动走出边界，则将它们在自由表面边界和水底边界处通过镜像反射使其返回水域。图1给出了这一线性波浪场中粒子在t=800 s时的空间分布和浓度分布，其中x=0处的竖直线代表粒子的初始位置。由粒子的空间位置分布可得到粒子分布的水平中心位置x，将其除以相应的时间间隔t可以得到粒子整体漂移的平均速度，图2给出了数值模拟得到的U以及欧拉描述的解析解（17b）的数值，二者趋向一致，表明在波浪场中粒子扩散过程中存在以式（17b）速度为对流速度的整体漂移。

上述一致性的原因是在于粒子整体漂移速度U是由于方程（18）中右端第一项所决定的，而第二项在统计意义上不会对平均运动产生影响。所以，仅由第一项的时间积分（可选择跟踪不同水深处的粒子）就可以得到Stokes漂移速度，图3给出了这一拉格朗日描述的Stokes漂移速度的沿水深分布，图中也给出了式（14）的解析求解的结果，由图3可见二者结果一致。

图1 计算模拟波浪场中的粒子漂移

图2 模拟得到的Stokes漂移速度（虚线）和解析解（式（17b））的结果（细实线）

图3 模拟得到的粒子Stokes漂移速度（空心圆圈）和解析解（式14）的结果（细实线）

由以上结果也可确定水深平均方程（16）中的离散系数K，即拉格描述确定的离散系数，计算式为

以上结果达到稳定状态时（t≥h2/Dz=1 800 s）粒子沿水平方向分布应呈正态分布，为了验证这一点，图5给出了t=1 800 s时刻粒子空间分布（上图）和粒子个数水平分布（下图）以及对应的理论概率正态分布，结果显示粒子的水平分布最终可以趋于正态分布。

图4 离散系数随时间的变化

图5 粒子追踪法达到稳态时粒子的空间分布（上图）和粒子沿水平分布及理论分布曲线（下图）

3 Stokes漂移效应欧拉描述的数值验证

前面第1节通过将方程（1）中的波浪速度场取为一阶波浪速度，然后建立波浪周期平均的浓度扩散方程，所得到的方程中对流速度即为Stokes漂移速度，其引起浓度在随波浪作周期性波动的同时还沿波浪传播方向上漂移。为了直观的显示这一欧拉描述的物理过程，这里通过数值求解方程（1）在一阶波浪速度场中的浓度扩散来直接给出浓度随波浪运动和扩散的过程，进而可以显示第1小节欧拉描述的Stokes漂移效应。

为了考虑自由表面波动所引起的计算区域的变化，计算中通过以下σ坐标变换将变动的计算区域转化为固定的计算区域：0≤σ≤1，变换前和变换后的计算区域如图6所示。

图6 σ-坐标系把直角坐标中的不规则的区域转化为矩形区域

以上方程的上下两侧边界条件为浓度梯度为零：

左右两侧边界条件取浓度为零：

模拟针对沿水深均匀分布的线源在波浪场所产生的扩散问题，对应的初始条件为

式中，M是注入的浓度总量，δ（ξ）是狄拉克（Dirac）函数。

用有限差分方法离散方程（21）各项，并用ADI格式求解。为了和第2节中的结果进行对比，水深和波浪条件与第2节中的一致。具体计算条件为：模拟区域的长度是80 m，初始线源在x=20 m处，网格间距深度方向为0.1、水平方向为0.1 m，时间步长为0.01 s。图7给出了对应于图5的t= 800 s时刻流场中浓度分布。由图可见，浓度在波浪作用下产生扩散的同时，还存在沿波浪传播方向的漂移。漂移的速度即为式（13）中的Stokes漂移速度。这里通过求这一漂移的水深平均速度U来说明这一点，该速度为

式中C为水深平均浓度，c（i，j）为网格点（i，j）处的浓度，Δξ为水平网格间距。上式中所得的浓度漂移速度与水深平均Stokes漂移速度式（17b）及粒子追踪法得到的粒子平均漂移速度在所计算的波况下的结果相近（0.03 m/s，见图2），图7也标出了这一速度所引起的浓度中心的水平位移UΔt。另外，图7中浓度扩散的等浓度线和图1中的下图也基本一致。但由于数值模拟存在数值耗散，所以在扩散系数D取一致的情况下，数值模拟结果的扩散要比粒子追踪法的要快，即图7中浓度的最大值要比图1中的最大值要小。

图7 释放800 s后物质浓度等值线

如上所述计算中引起浓度扩散的波浪速度场（u，w）取为一阶波浪速度式（2），而不再额外加入Stokes漂移速度us。数值模拟证明，虽然没有加入Stokes漂移速度，但该速度引起的漂移效应可由周期性波动的线性波浪速度与周期性波动的浓度分量相互作用（方程（1）中对流项u∂c/∂x+w∂c/∂z所导致）而形成（具体细节见第1节中给出的解析分析）。

以上结果的物理过程可由第1节中解析分析看出，即浓度在波浪场中的扩散过程包括两部分，随波浪快速波动的过程（式（5）中εc(1)）和波浪周期时间平均的浓度缓慢漂移和扩散过程（式（5）中c(0)）。

4 实际应用

将以上Stokes漂移效应对应的波浪引起的浓度沿波浪方向的平均浓度输移通量为：

该通量表达投放于海洋中的物质浓度随波浪的漂移。为了直观显示这一现象，图8给出了实验室中在波浪场中所投放的墨水向岸漂移现象。所对应的波浪在离岸以30°斜向（图中3个测量杆与岸线垂直）传向海岸的波浪（波高0.05 m，周期1.5 s），海岸的坡度为1∶100，墨水投放点距岸10.5 m，位于破波带外（波浪破碎点距岸9 m），墨水投放形式为连续源。由图可见墨水在不破碎波浪作用下呈现向岸漂移的移动，移动距离可由Stokes速度计算出，如第4个图片相对第1个图片的时间间隔为Δt=45 s，由对应的水面处的Stokes漂移速度[uc]z=0=0.048 m/s（按公式（13）计算，并取墨水轨迹线中点处的波高0.055 m），可得到从这两个图之间的墨水漂移距离为：

由于餐饮企业规模较小，经济实力一般，使得餐饮企业资产信用度低，而国家也没有政策性支持，因此餐饮企业很难进行融资。银行和金融机构在进行融资的过程中，要对被融资的企业进行资产评估，评估达到一定的标准才能进行融资，银行和金融机构一般都需要把风险降到最低。餐饮企业资产额不高，企业自身偿还能力有限，这些因素都是导致其融资难的原因[3-7]。

该距离相当于1.5倍的当地波长（1.44 m），这一结果可由图直接看出，因为图中斜的亮线为波峰线，而从第1个照片到第4个照片墨水移动距离约为1.5倍波峰线间距离（波长）。可见，破波带外墨水（污染物）漂移主要受Stokes漂移效应控制。但进入破波带内之后，墨水不但受Stokes漂移驱动而且还受波浪破碎产生的沿岸流（其方向为平行海岸方向）驱动，所以墨水轨迹趋向平行海岸，如图中最后两个照片所示。

以上的实验结果显示出Stokes漂移速度对于不破碎波浪情况是可以引起流体中浓度向波浪方向漂移，这一漂移运动在破波带内也是存在的，具体结果见Winckler等（2014）的研究。对实际海洋情况，Monismith等（2004）通过几个现场观测结果建议在建立内陆架海域的物质输移扩散模型时应注意考虑Stokes漂移速度的影响，因为他们的观察表明该漂移速度量级经常和内陆架海域观测到的其他漂移流速相当或较之更大。

图8 墨水运动轨迹及对应波高和沿岸流速分布（金红等，2006）

5 结语

本文讨论了采用欧拉描述来考虑波浪中物质浓度输移扩散Stokes漂移效应的原理，表明当仅将波浪场取为一阶波浪速度，而不额外添加Stokes漂移速度，Stokes漂移效应也可以自然地产生出来，产生的原理是周期性波动的波浪速度与周期性波动的浓度变化的相互作用。这一原理在所推导出的波浪周期上时间平均的浓度输移扩散方程中表现为对流速度即为Stokes漂移速度，该速度引起了浓度除了随波浪周期性的波动外，还存在沿波浪传播方向上的漂移。这一现象也可以由本研究所进行的粒子追踪法浓度扩散过程（对应拉格朗日描述）和数值求解垂直二维浓度扩散方程的计算结果（对应欧拉描述）得到验证。由以上理论分析所得到Stokes漂移效应产生的离散系数也与以往研究所得到的结果一致。研究中也根据该欧拉描述方法讨论与解释了物理模型实验中观察到的破波带外波浪引起的浓度漂移现象。

Fischer H B,List J E,Koh C R,et al,2013.Mixing in inland and coastal waters.Elsevier.

Henderson S M,Allen J S,Newberger P A,2004.Nearshore sandbar migration predicted by an eddy-diffusive boundary layer model. Journal of Geophysical Research：Oceans(1978-2012),109(C6).

Law A W K,2000.Taylor dispersion of contaminants due to surface waves.Journal of Hydraulic Research,38(1):41-48.

Longuet-Higgins M S,1953.Mass transport in water waves.Philosophical Transactions of the Royal Society of London A:Mathematical, Physical and Engineering Sciences,245(903):535-581.

Mei C C,Fan S,Jin K,1997.Resuspension and transport of fine sediments by waves.Journal of Geophysical Research:Oceans (1978-2012),102(C7):15807-15821.

Monismith S G,Fong D A,2004.A note on the potential transport of scalars and organisms by surface waves.Limnology and Oceanography,49(4):1214-1217.

Patil S,et al,2007.Shear flow dispersion under wave and current.China Ocean Engineering,21(4):549-560.

Röhrs J,Christensen K H,Vikeb F,et al,2014.Wave-induced transport and vertical mixing of pelagic eggs and larvae.Limnol.Oceanogr, 59(4):1213-1227.

Shen L D,Zou Z L,2014.A theoretical solution to dispersion coefficients in wave field.Ocean Engineering,88:342-356.

Stokes G G,1847.On the theory of oscillatory waves.Trans Cambridge Philos Soc,8:441-473.

Taylor G,1953.Dispersion of soluble matter in solvent flowing slowly through a tube//Proceedings of the Royal Society of London A: Mathem-atical,Physical and Engineering Sciences.The Royal Society,219(1137):186-203.

Van den Broeck C.Taylor dispersion revisited.Physica A:Statistical Mechanics and its Applications,1990,168(2):677-696.

Winckler P,Liu P L F,Mei C C,2013.Advective Diffusion of Contaminants in the Surf Zone.Journal of Waterway,Port,Coastal, and Ocean Engineering,139(6):437-454.

Wolk F,2003.Three-dimensional Lagrangian tracer modelling in Wadden Sea areas.

金红，邹志利，邱大洪，等，2006.波生流对海岸污染物输移的影响.海洋学报，28（6）：144-150.

袁德奎，林斌良，陶建华，2004.波浪作用下污染物的混合和离散.水利学报，8：76-78.

（本文编辑：袁泽轶）

Eulerian description of wave-induced Stokes drift effect on the advective diffusion of tracer concentration

YAN Sheng,ZOU Zhi-li
（1.State KeyLaboratoryof Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China）

The Eulerian description of wave-induced Stokes drift effect on the advective diffusion of tracer concentration is studied showing that this effect can be automatically accounted for in the wave-averaged advection-diffusion equation of concentration in linear wave field,as the advection velocity of the equation is just the Stokes drift velocity.The equivalence of this Eulerian description to the Lagrangian description is verified by comparing the numerical results of vertical distribution of Stokes drift velocity by the particle tracking method with the Eulerian results,with the former one being a Lagrantian type description.The Eulerian description of Stokes drift effect is also illustrated numerically by solving the advection-diffusion equation in σ-coordinates,which shows the drift of concentration driven by Stokes drift.The observed wave-induced concentration drift in the laboratory experiments is also presented to show the drift of concentration in practical wave field.

Stokes drift velocity;concentration advective diffusion equation;linear wave;Taylor dispersion;Eulerian description

P731.22

A

1001-6932（2017）04-0416-08

10.11840/j.issn.1001-6392.2017.04.008

2015-12-17；

2016-03-31

国家自然科学基金（11272078；51221961）。

闫圣（1987-），博士研究生，主要从事海岸水动力学研究。电子邮箱：yansheng11106082@mail.dlut.edu.cn。