广西万尾岛金滩沿岸输沙计算与分析

郭雅琼，马进荣，邹国良

（1.南京水利科学研究院港口航道泥沙工程交通行业重点实验室，江苏南京210029；2.河海大学港口海岸与近海工程学院，江苏南京210098）

广西万尾岛金滩沿岸输沙计算与分析

郭雅琼1，2，马进荣1，邹国良1

（1.南京水利科学研究院港口航道泥沙工程交通行业重点实验室，江苏南京210029；2.河海大学港口海岸与近海工程学院，江苏南京210098）

依据CERC公式，年内代表浪向作用下，广西万尾岛金滩平直岸滩中部泥沙分别向东西两侧净输沙，意味着金滩中部有淘刷趋势而两端有淤积趋势，而实际上岸滩中部滩面长年基本稳定、未有明显侵蚀现象。分析认为公式计算成果反映的输沙特征定性仍然是正确的，岸滩能够维持稳定是因为还存在自海向岸的横向输沙补给沙源。当岸滩并非平直且足够长时，应完整分析纵、横向输沙才能更为合理地反映岸滩泥沙运动特征。

万尾岛；沿岸输沙；CERC公式；岸滩稳定性

沙质海岸前沿沙滩的泥沙输运特征一直是海岸工程界关注的问题，沿海岸线走向截取一段海岸和岸滩单元，则存在与沿海岸线走向一致的纵向泥沙运动和垂直海岸方向的横向泥沙运动，前者常被称为沿岸输沙。目前，计算沿岸输沙的公式相对较多，其中CERC公式（Krumbein，1944；安永宁等，2010；冯秀丽等，2009）应用最为广泛，该公式被美国陆军工程兵团最新编制的《海岸工程手册》（2003）收录。该公式计算方法属于波能流法（白玉川等，2014），一般适用于相对平直且沿岸破碎波高变化相对较小的岸滩。横向输沙方面的成果主要反映在沙滩的剖面形态的计算，影响因素包括沙滩泥沙粒径、波浪动力强度及作用水位等，由于水位的周期性变化、波浪动力的强弱变化、季节性水沙动力变化等都对沙滩剖面形态有直接影响，裸露沙滩还直接受到向岸与离岸风力作用而输运，因此暂时还没有适用于各要素变化特征的横向输沙计算公式。正是由于横向输沙计算的复杂性，在分析计算岸滩稳定性时，往往只依据相对成熟的经验公式计算横向输沙，并且有时还忽略了横向输沙计算公式所适用的条件。本文以分析广西东兴市的万尾岛金滩沿岸输沙为例，探讨了沙质海岸岸滩稳定性的动力要素与泥沙运动的周期性变化特征，计算了其沿海输沙情况，分析了成果的合理性。

1 研究岸滩的基本情况

研究岸滩称为金滩，是万尾岛南岸滩，位于广西防城港地区的珍珠湾湾口西侧。万尾岛原为一离岸海岛，约于上世纪七十年代修建两条堤坝，连通相邻的巫头岛与大陆相接，万尾岛成了半岛的最南端，直面北部湾，见图1。

比较早期图片及近期卫片可见，近半个世纪以来，万尾岛南岸的岸线形态并没有因为连岛堤坝建设发生有明显改变，岸线保持平直、长度也几乎不变。

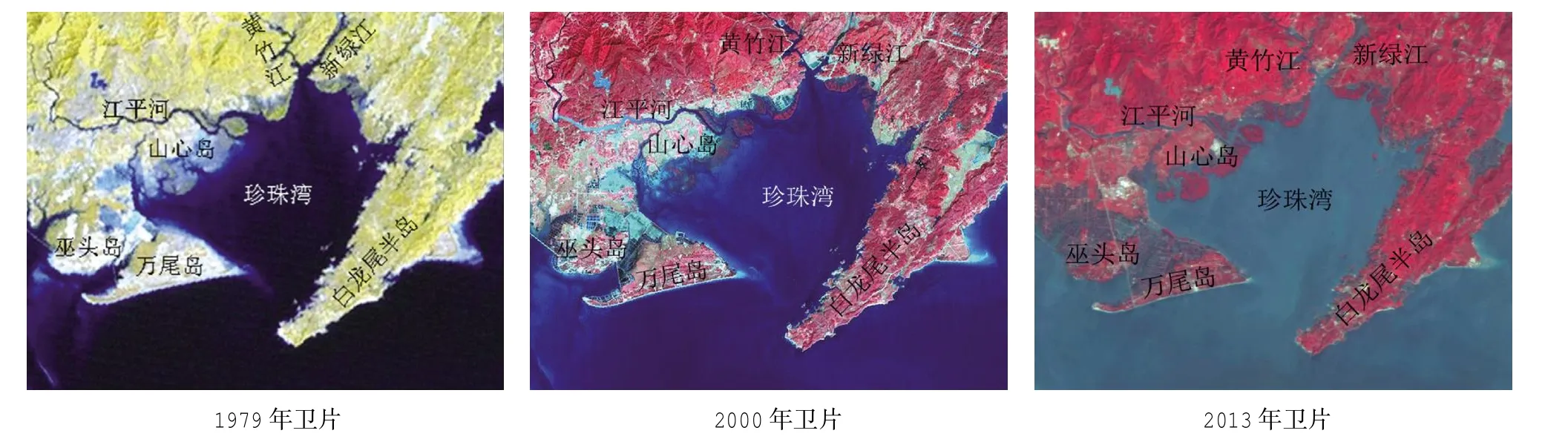
图1 珍珠湾不同年份卫片

金滩岸滩长约7.8 km，滩前0 m等深线（文中基面均为白龙尾理论最低潮面）与岸线走向几乎平行，距岸约270 m左右；金滩西侧水深相对较浅，0 m线距岸线介于0.8 km~2.8 km之间，见图2。金滩水域介于珍珠湾湾口与北仑河河口湾之间，东、西侧分别有白龙尾半岛和茶古岛突入海侧，对东向和西向波浪形成一定掩护，但南向或偏南向的波浪均可直接传播至金滩前水域，且偏南向的波浪正是北部湾水域的强浪向。

万尾岛南岸前沿滩涂区的泥沙中值粒径介于0.114~0.649 mm（2013年10月测），沙质柔软、色泽金黄，故称金滩。金滩西侧附近水域泥沙与金滩区域无明显差别，但东侧珍珠湾内的泥沙粒径分布范围更广，湾内河口局部区域泥沙明显粗于金滩，湾内红树林区则相对较细、甚至呈现为淤泥状。

金滩水域的潮汐属浅水分潮影响较显著的正规全日潮，最大潮差可达5.39 m、平均潮差约2.55 m。潮流流速一般小于0.30 m/s，近岸小、远岸大，由于涨潮历时一般长于落潮历时，通常潮段平均流速有落潮大于涨潮的特点，珍珠湾湾口深槽落潮流速大潮时可达0.80 m/s。

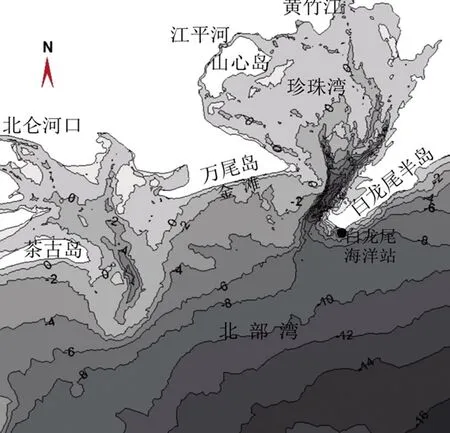
图2 金滩附近水下地形图

2 沿岸输沙计算

2.1 沿岸输沙计算模型

沿岸输沙的机理是波浪掀沙、沿岸流输沙（吴宋人，1999）。金滩水域泥沙粒径表明该海岸属典型沙质海岸，而且岸线平直（接近ENE-WSW走向），适宜采用CERC公式计算，表达式如下：

式中，Iy为重量输沙率，Py为波能流沿岸分量，K为经验系数，E为单宽波峰线长度上的总波能，Cg为波群速度，θb为破碎波波峰线与等深线的交角（破波角）。

采用CERC公式进行计算时，经验系数K对计算结果有着重要影响。Komar等（1970）结合Watts（1953）的实验数据，并加入1970年的现场资料，将系数K修正为0.77。CERC公式没有考虑坡度、周期、粒径、破波类型等因素，跟许多实际情况有一定出入，Wang（2002）等实验资料显示，利用该方法预测崩破波时计算比实测大2.5倍，卷破波时大7倍，仅适用于粒径0.2~0.4 mm的范围。后来许多学者对系数K作了相关修正，如Del Valle（1993）根据实验室资料得出K与泥沙中值粒径D50的函数关系：

2.2 破碎波浪要素计算模式

沙质海岸的纵向或沿岸输沙大部分发生在波浪破碎区（有的达90%），其余发生在破碎波区以外的浅水区。在破波带，大多数沿岸输沙是以悬移质形式搬运的。因此沿岸输沙计算时，破碎波参数的推算对输沙方向及量级判断起着至关重要作用，进而也会影响岸线变形趋势。外海不同浪向和波高往近岸传播时，其波浪破碎位置、破碎波高等参数是不同的。通过现场波浪观测来提供破碎波要素几乎是不现实的，其一方面耗费巨大，另一方面波浪破碎位置现场确定仍有一定难度。因此，国内外沿岸输沙的破碎波要素一般采用数值推算来获得。目前国内外工程界沿岸输沙计算所需的破碎波要素推算方法主要有：波向线法和波浪数学模型模拟方法。本文采用可模拟波浪折射、绕射及破碎等变形现象的SWAN波浪数学模型（SWAN team，2008；徐丽丽等，2015）进行破碎波要素计算。

SWAN模型采用波作用谱平衡方程描述风浪生成及其在近岸区的演化过程。在笛卡尔坐标系下，波作用谱平衡方程可表示为：

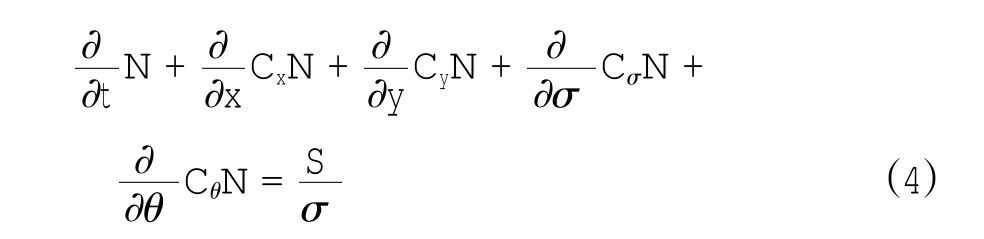
式中，N波浪作用密度谱；σ为波浪的相对频率，θ为波向；x、y为笛卡尔平面坐标；Cx、Cy分别为x、y方向的波浪传播速度，Cσ、Cθ分别为σ、θ空间的波浪传播速度；S是以波作用谱密度表示的描述波浪变形的源项，包括风能输入、由于底摩擦、白浪、水深变浅引起的波浪破碎等导致的能量耗散和波与波之间的非线性相互作用，并假设各项可以线性叠加（李绍武等，2012）。

波浪传播速度可表示为：

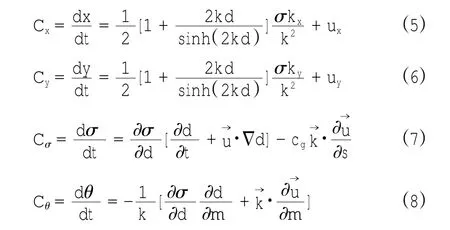
其中，d为水深，s为沿θ方向的空间坐标，m为垂直于s的坐标为波数，d为水深，为流速，算子∂/∂t定义为：

SWAN模型采用全隐有限差分格式求解控制方程，模型计算区域陆域边界的波能交换量为0，在计算区域的开边界需要给出波能交换量。通过数值求解（4）式，可以得到风浪从生成、成长直至风后衰减的全过程；也可以描述在给定恒定边界波浪时，波浪在近岸区的折射和浅水变形。

本次波浪数学模型计算域覆盖了防城湾、珍珠湾以及北仑河口海湾，模型西边界至越南茶古岛西侧，东边界至企沙半岛中部，南边界位于-25 m等深线附近，模型东西长45 km，南北长50 km。

2.3 计算条件

根据1969-1982年白龙尾半岛南端白龙尾波浪站多年统计的波浪资料（中国海湾志编纂委员会，1993）来看（测站位置见图2），本海区波浪以风浪为主，累年统计的风浪出现频率达99%。该站强浪向为SE向，最大波高为4.1 m，其次为SSE方向，出现最大波高为3.7 m；常浪方向为NNE向，次常浪向为NE向，这两个方向的波浪出现频率合计为48%，各向最大波高和出现频率玫瑰图见图3和表1。

万尾岛南侧金滩前岸线走向接近ENE-WSW方向，金滩前中部近岸侧等深线走向与岸线走向基本一致。在岸线走向范围内，外海可直接传播至海岸且总频率在10%以上的浪向有S、SE和SSW。此外，在岸线走向范围内的E向浪（频率为5.7%）受白龙尾半岛的阻挡，其对金滩前沿水域的破碎波浪要素影响较小。NNE和NE向风浪频率虽然较高，但属离岸风。综上，金滩前沿沿岸输沙计算主要选S、SE、SSW三个方向，兼顾邻近浪向的波浪作用，通过作用时间（频率）反映。

2.4 计算结果

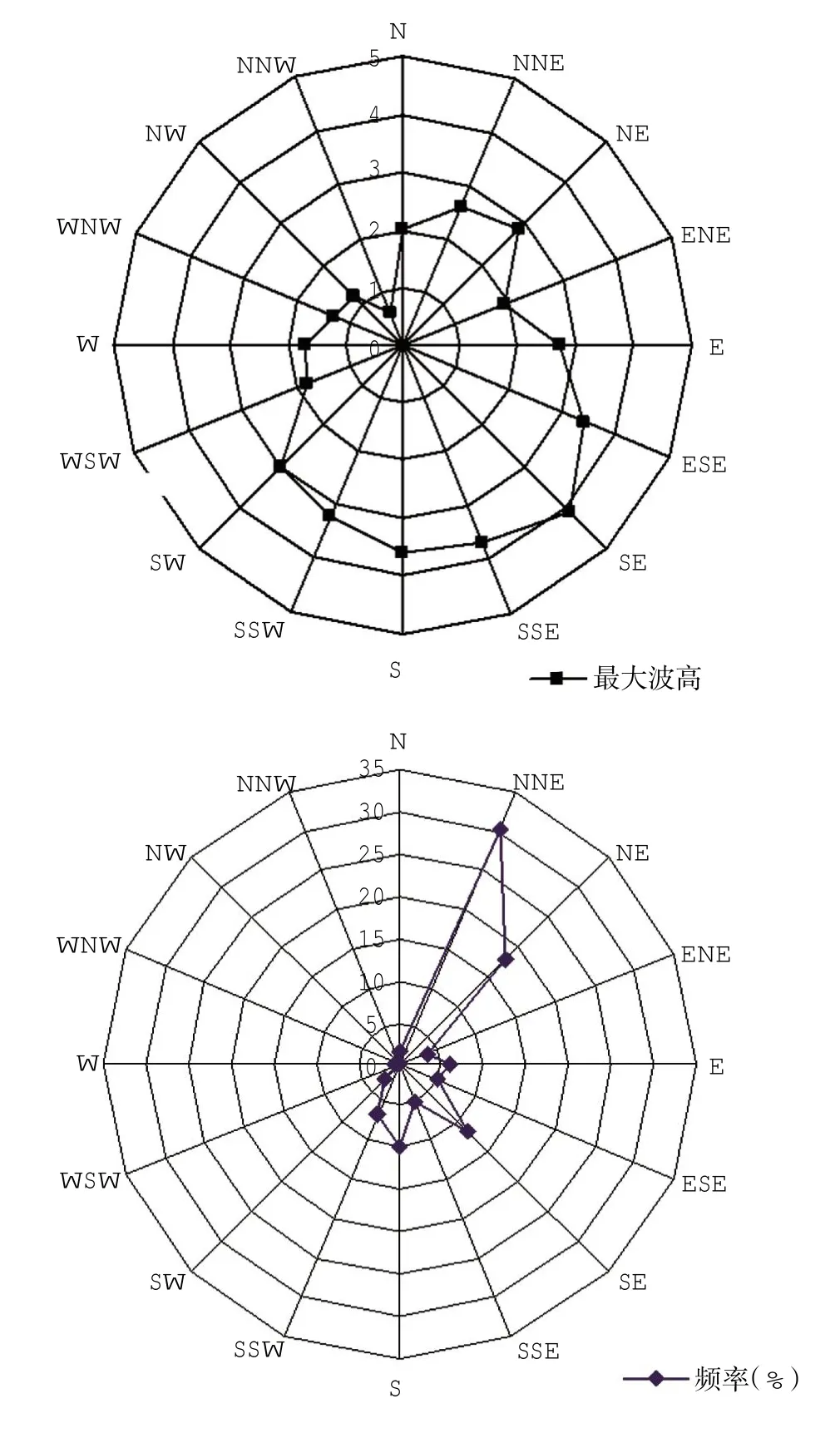
图3 白龙尾站最大波高及波高频率玫瑰图

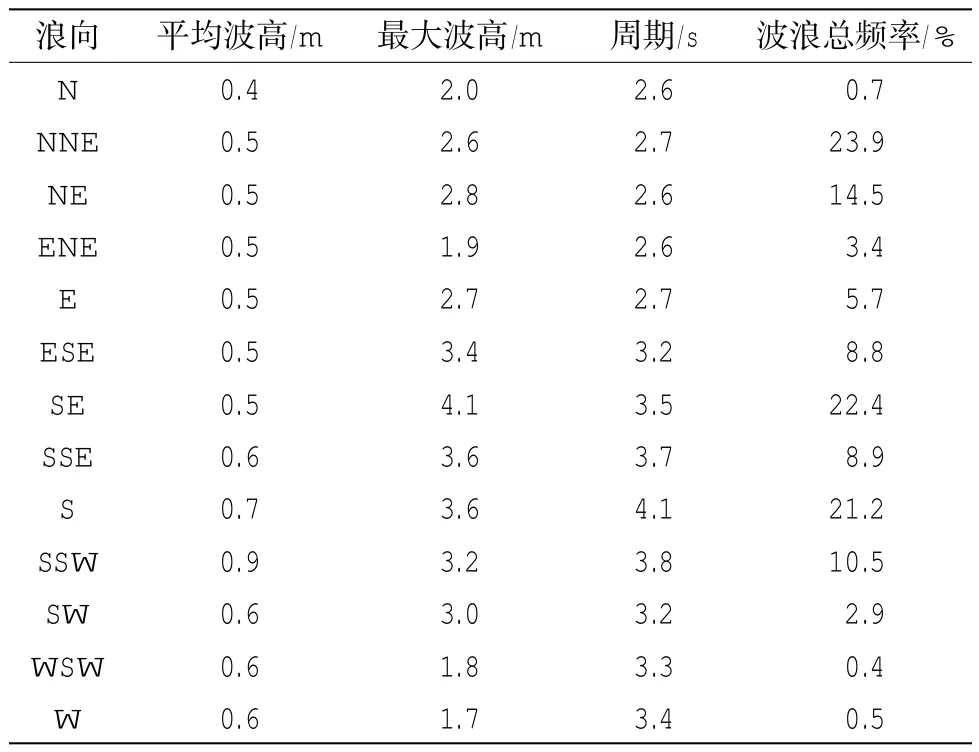
表1 白龙尾站分向波浪统计特征（中国海湾志编纂委员会，1993）

在金滩岸线前每隔1 km布置1个断面，共布置7个断面（图4）进行沿岸输沙计算。根据白龙尾波浪站的波浪统计资料，通过调试外海边界入射波浪条件使得海洋站位置处的波高等参数与统计资料一致，以此来确定外海边界波要素，进一步根据波浪频率、波向以及分级波高推算破碎波要素。破碎波要素通过能量耗散来判断，将近岸处波能开始明显出现大幅度衰减位置作为破碎波要素选取的位置。表2给出了通过上述方法提出的S、SE、SSW三个浪向各断面破波参数。

表3给出了现状条件由CERC计算出的各断面的沿岸输沙量。根据现状条件下沿岸输沙量计算结果表明，金滩前1#-4#号断面，即金滩中部至金滩东侧沿岸净输沙方向为由西向东，而金滩西侧（5#-7#）沿岸净输沙方向为由东向西。金滩东西两侧的断面位置处年输沙量较大，1#和7#断面位置处的年净输沙量分别为5.96万m3和5.79万m3。往金滩中部区域年输沙量逐渐减小，其主要原因是S向浪传至近岸金滩中部和东西两侧时因等深线走向变化较大导致波浪折射作用下的破碎波向发生较大的改变。金滩东侧1#-4#由西向东的年净输沙量由5.96万m3减少至0.85万m3；而金滩西侧5#-7#断面处由东向西的年净输沙量由5.79万m3减少至1.31万m3。

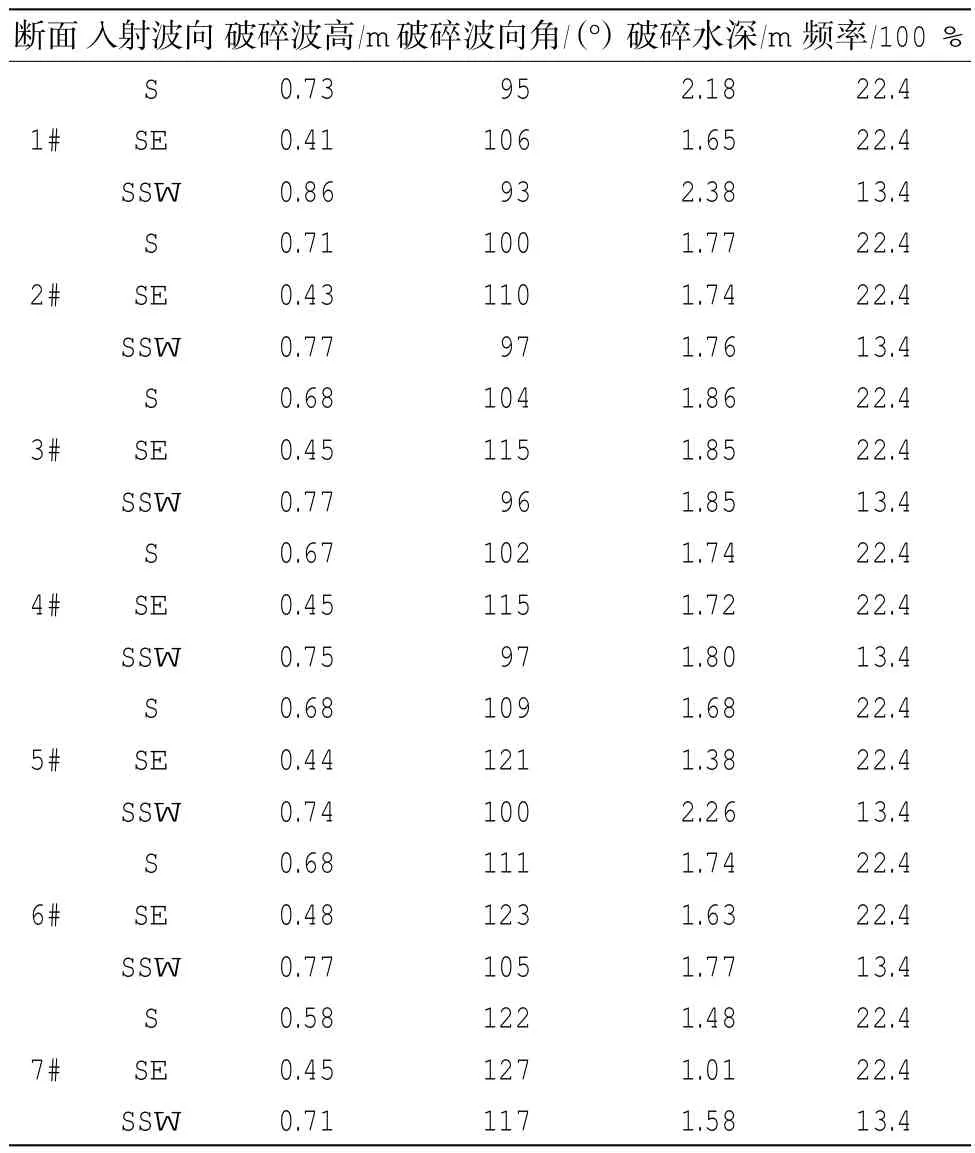
表2 现状条件下不同断面破波参数

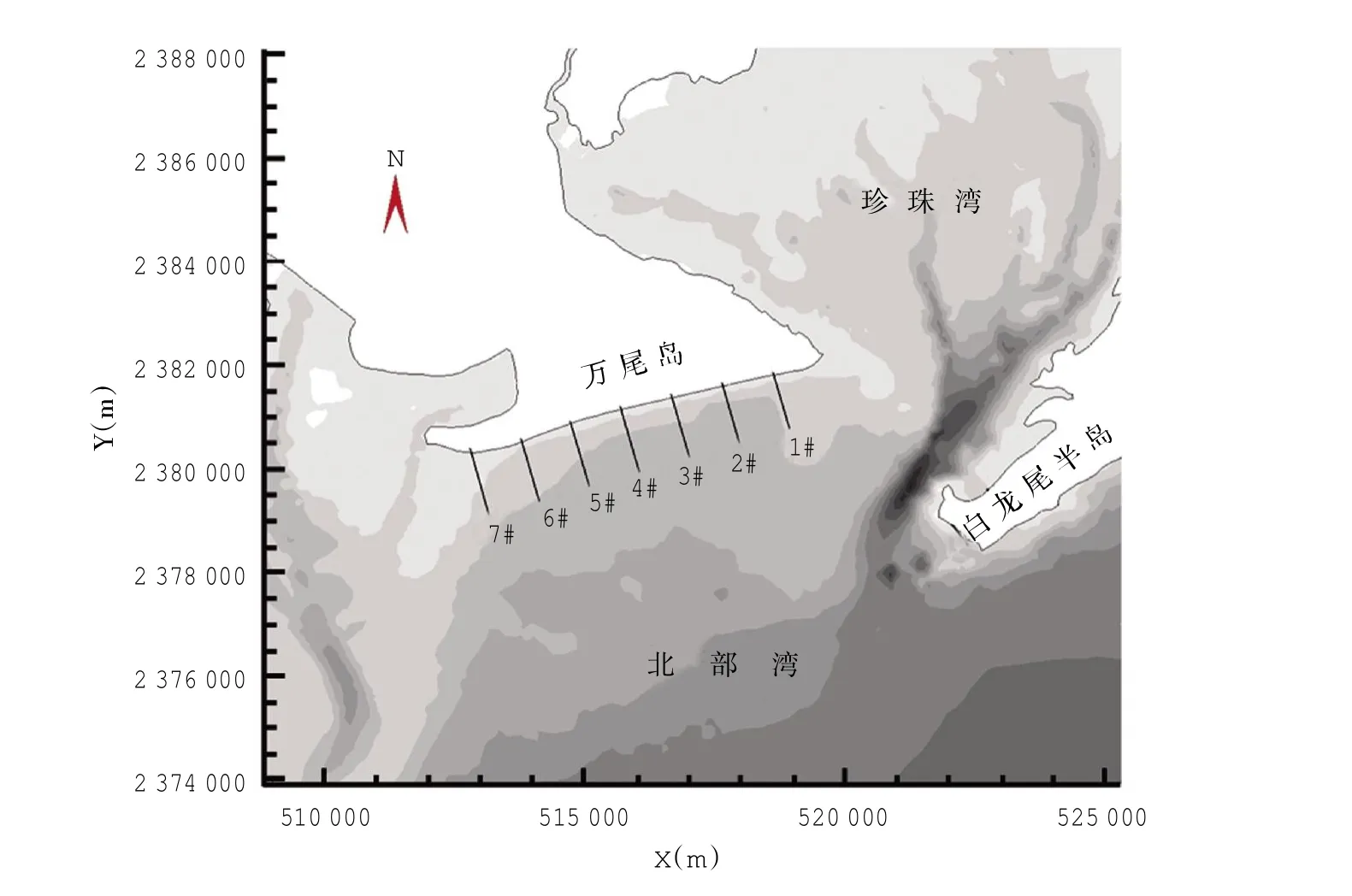
图4 金滩前沿计算断面位置示意图

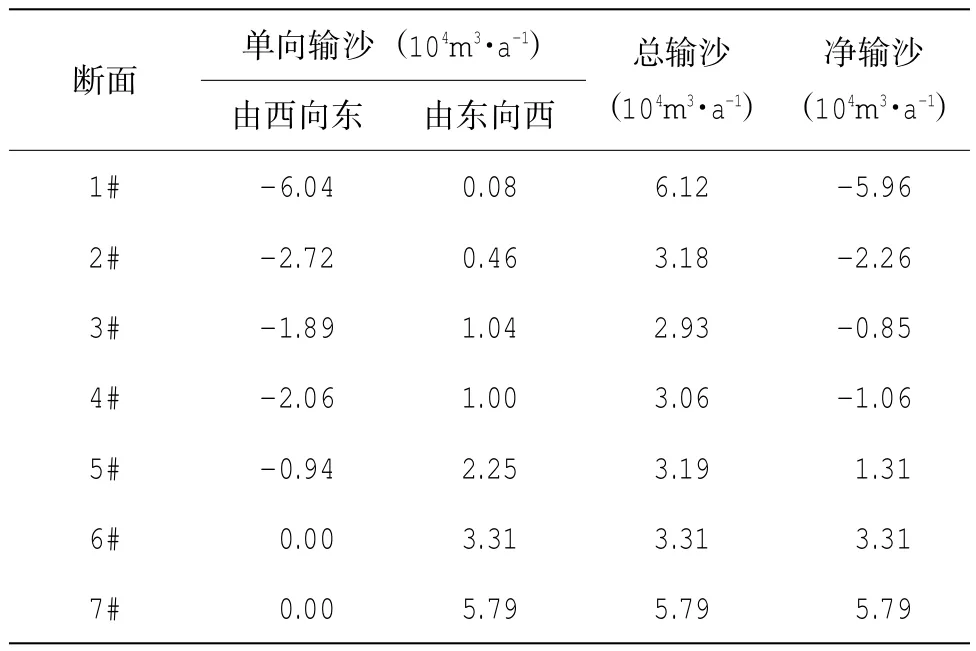
表3 各断面沿岸输沙量计算结果

3 岸滩泥沙动力分析

沿岸输沙的结果提示岸滩将是不稳定的，中部有淘刷趋势而两端有淤积趋势。金滩海岸是2013年才开始固化，之前是自然状态，这意味着，如果海岸中部前沿淘刷、两侧淤积，显然岸线形态会发生相应的变化，会向弧形海岸发展。事实上近半个世纪以来，金滩海岸保持顺直。

沿岸输沙计算公式的原理正确、应用广泛，不存在明显不适用的制约因素；计算条件的概化、参数的取值可能会引起一些偏差，但不至于引起定性的差异。如果暂且不管陆域岸线，而是审察0 m线和-2 m线，可见清晰的弧形状态；0 m形的弧形犹为明显，-2 m线大致呈弧形状态，其东段在接近珍珠湾湾口处向南急转外。

沿岸输沙计算只考虑了波浪动力的纵向动力因素，忽略了波浪的横向动力作用。-5 m线以浅等深线的弧形形态表明，南向或偏南向波浪的波能有向金滩中部（等深线凸出）的位置集中趋势，因此床面泥沙有随波能输运方向携带泥沙输运的可能。分析波浪和潮流共同作用下的岸滩泥沙运动有助于更好地了解岸滩演变的机理。

3.1 潮流起动分析

泥沙起动流速计算采用武汉水院公式（张瑞瑾，1998；张红武，2012）：

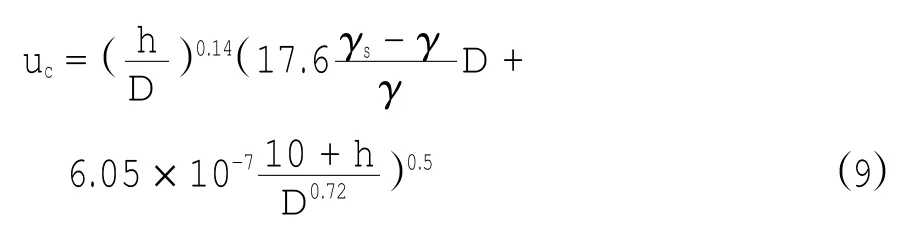
式中，uc为起动流速；h为水深；D为泥沙粒径；r、rs分别为水和沙粒的容重。

金滩水域不同水深条件下分组泥沙粒径潮流起动流速计算成果列于表4，金滩前沿1 km范围内附近水域涨、落潮最大流速不超过0.35 m/s，一般条件下的潮流流速不足以起动滩面泥沙，但是洪季，珍珠湾承纳了江平河、黄竹江等几条河流的洪水，湾口附近落潮流速会有所增大，金滩东端浅滩泥沙将有起动输运发生，落潮流越过浅滩滩脊后折南西侧，输运的泥沙有向滩中补给趋势。图5为金滩附近水域涨、落急流态（郭雅琼等，2015），金滩中部偏西位置形成涨、落潮分汇流点，落急时刻金滩东侧珍珠湾和西侧北仑河海湾的落潮流在此汇聚。北仑河上游是区域性的强降雨区（陈宪云等，2015），洪季流量较大，金滩西端浅滩泥沙也有输运发生，输运方向为南偏东，这也正是西端浅滩南北向拉伸较长的主要原因。

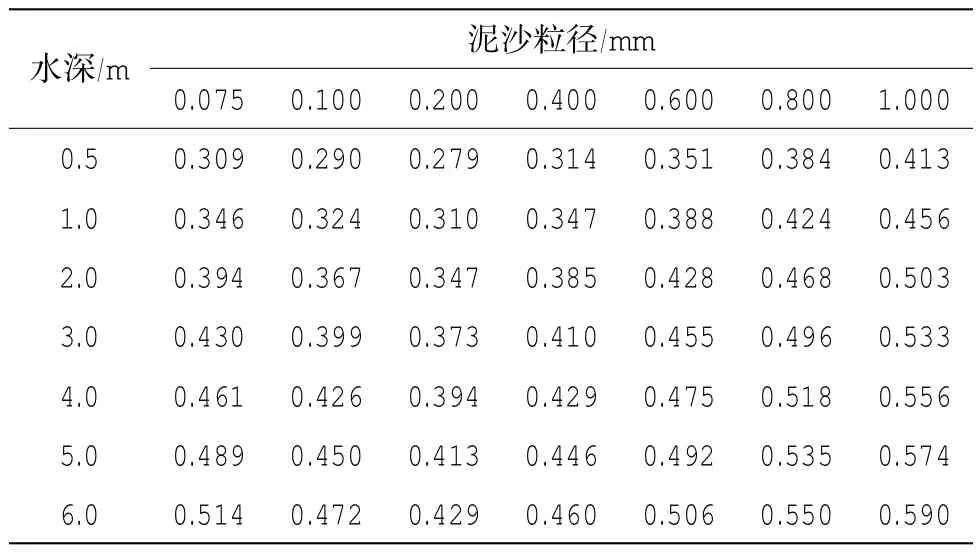
表4 潮流作用下的起动流速计算表（单位：m·s-1）

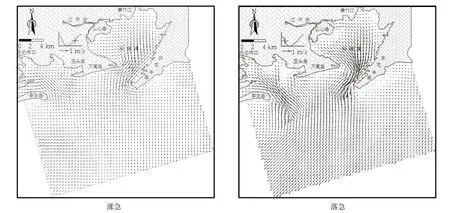
图5 金滩附近水域涨、落急流态示意图（郭雅琼等，2015）

3.2 波浪起动分析

泥沙粒径较粗时，波浪对底床泥沙的作用可按日本学者佐藤、田中（管君阳，2011）公式加以分析：

完全移动临界式：

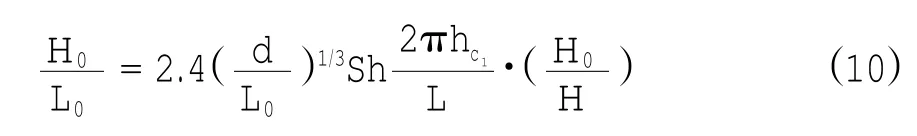
表层移动临界式：

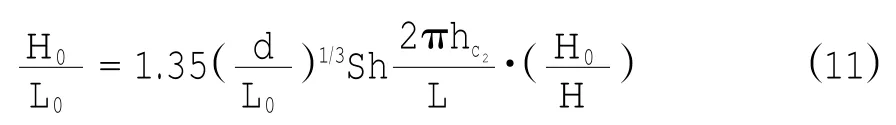
式中：H0、L0分别表示深水波高和波长；d表示泥沙中值粒径；L、H、分别表示水深hc处的波长和波高分别表示海底泥沙完全移动和表层移动临界水深

以南向浪为代表浪，计算得到金滩水域分级水深条件下不同泥沙粒径组的起动波高，列于表5。从起动波高看，较细部分的泥沙在水深相对较小时，起动机率较大。金滩水域的潮差较大，日变幅较大，中低潮位处的泥沙受波浪起动输运的机率更大。

珍珠湾NNE向波浪频率高达23.9%，金滩水域大部分区域有一定的遮蔽条件，但东端浅滩受该方向波浪影响较大，东端附近-2 m等深线在湾口附近向南急转可能与该方向的波浪作用有密切关系。

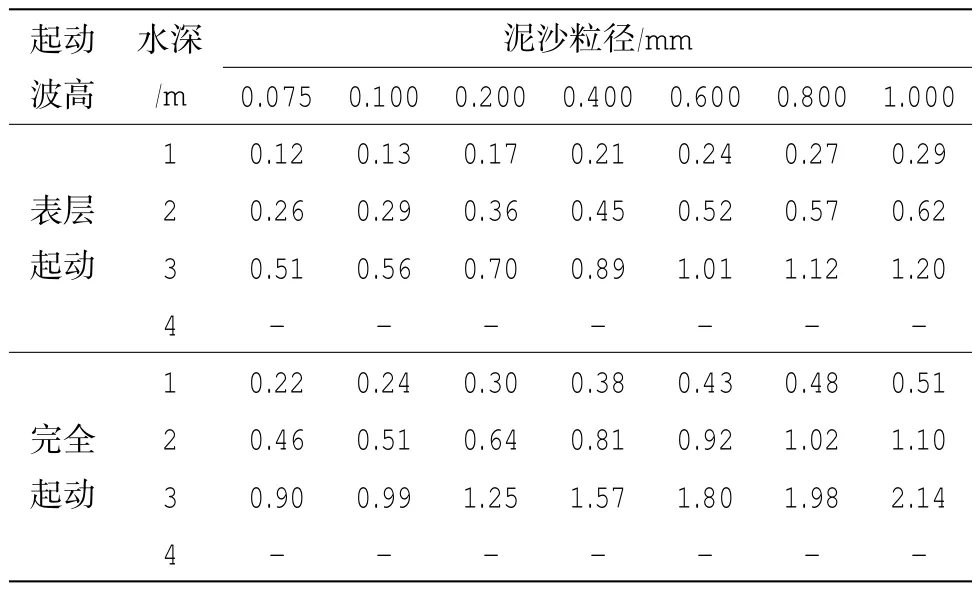
表5 起动波高计算表（S向代表浪，H0=0.7 m，T=4.1 s）

4 结语

以广西万尾岛直面南向风浪的金滩为例，通过沿岸输沙计算发现存在年内不平衡输沙特征，与海岸长期稳定的自然现象相矛盾，结合岸滩水域的潮汐潮流特征、水下地形形态，从潮流和波浪两种主要动力分析计算，揭示了这种类型的周期性稳定岸滩与不平衡沿岸输沙的和谐性，得到以下启示：

1）自然条件下，仅考虑白龙尾波浪站的S、SE和SSW向浪，金滩前波浪破碎引起的沿岸输沙趋势为金滩中部至东侧沿岸净输沙方向为由西向东，金滩西侧的沿岸净输沙方向为由东向西，且金滩东西两侧的年净输沙量较大，泥沙活动性较强。

2）稳定的岸滩并不意味着泥沙没有输运，也不仅是沿岸输沙在一定周期内的动态平衡状态，应包括岸滩纵向和横向输运的综合动态平衡。在平直海岸，采用CERC公式计算所得到成果只能揭示沿岸方向的泥沙输运状态，要判断该海岸的稳定性往往不可忽略垂直岸线的横向输运，特别是当海岸长度有限时，应分析其两端的泥沙运动特征。

3）对于沙质海岸，波浪动力是岸滩泥沙输运的主要动力，当岸滩附近有入注河流时，考虑河流的季节性潮流动力潮动力变化才能更全面地描述岸滩泥沙输运的周期性演变特征。

Del Valle R,Medina R,Losada M A,1993.Dependence of coefficient K on grain size.Technical Note No.3026,Journal of Waterway,Port, Coastal,and Ocean Engineering,119(5):568-572.

Komar P D,Inman D I,1970.Longshore Sand Transport on beaches. Journal of Geophysical Research,75(30):5514-5527.

Krumbein W C,1944.Shore Currents and Sand Movement on a Model Beach.Shore Currents&Sand Movement on A Model Beach.

SWAN TEAM,2008.Swan user&technical manual(40.72A).Delft University of Technology.

U.S.Army Corps of Engineers,2003.Coastal Engineering Manual. Washington D C,USA:US Government Printing Office.

Wang P,Smith E R,Ebersole B A,2002.Large-scale Laboratory Measurements of Longshore Sediment Transport under Spilling Breakers.Journal of Coastal Research,18(1):18-35.

Watts G M,1953.A Study of Sand Movement at South Lake Worth Inlet, Florida.U.S.Army Corps of Engineers,Beach Erosion Board, Technical Memorandum,42.

安永宁，吴建政，朱龙海，等，2010.龙口湾冲淤特性对人工岛群建设的影响.海洋地质动态，26（10）：24-30.

白玉川，陈献，2014.莺歌咀附近岸段沿岸输沙率的计算与分析.泥沙研究，（5）：25-31.

陈宪云，董德信，郭佩芳，等，2015.北仑河口北冲西淤形成与环境因素的影响分析.海洋通报，34（2）：175-180.

冯秀丽，董卫卫，庄振业，等，2009.莱州湾东岸沿岸输沙率及冲淤演化动态分析.中国海洋大学学报（自然科学版)，39（2）：304-308.

管君阳，2011.杭州湾北岸冲淤演变及其对化工区工程响应.华东师范大学硕士学位论文.

郭雅琼，马进荣，邹国良，2015.东兴市金滩西部棕榈岛内水体交换数值研究//第十七届中国海洋（岸）工程学术讨论会论文集.北京：海洋出版社，438-443.

李绍武，梁超，庄茜，2012.SWAN风浪成长模型在近海设计波浪要素推算中的应用.港工技术，49（2）：5-7.

吴宋人，1999.海岸动力学.北京：人民交通出版社.

徐丽丽，肖文军，石少华，等，2015.WaveWatch III和SWAN模型嵌套技术在业务化海浪预报系统中的应用及检验.海洋通报，34（3）：283-294.

张红武，2012.泥沙起动流速的统一公式.水利学报，43（12）：1387-1396.

张瑞瑾，1998.河流泥沙动力学.北京：中国水利水电出版社.

中国海湾志编纂委员会，1993.中国海湾志第十二分册（广西海湾).北京：海洋出版社.

（本文编辑：袁泽轶）

Computation and analysis of alongshore sediment transport in Golden Beach of Guangxi

GUO Ya-qiong1,2，MA Jin-rong1，ZOU Guo-liang1
(1.NanjingHydraulicResearch Institute,KeySediment Research Lab of Harbors and Waterways of the Ministry of Communications, Nanjing210029,China;2.Hohai University,StateKey Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Nanjing210098,China)

Alongshore sediment transport,at the straights beach named as the Golden Beach of Wanwei Island in Guangxi province,is analyzed by CERC formula under annual wave condition.It shows that sediment transport direction is from the middle of the beach to both sides in E-W direction.It implies that the coast beach will erode at the middle while the two sides will silt.But the beach has kept well balance for years.A study is proceeding to explain the phenomena in this paper.The most important reason is that the cross shore sediment transport has just the opposite effect on the beach evolution to alongshore transport.The beach that can be able to maintain stability is due to transverse sediment transportation supplying sand source from the sea to shore.Both longitudinal and cross-shore sediment transport should be analyzed to reflect characteristics of sediment movement on beach reasonably,especially when the beach is not long enough or not straight.

Wanwei Island;alongshore sediment transport;CERC formula;beach stability

TV148.5

A

1001-6932（2017）04-0468-07

10.11840/j.issn.1001-6392.2017.04.014

2016-05-01；

2016-06-21

郭雅琼（1987-），博士研究生，主要从事河口海岸水动力、水环境和泥沙研究。电子邮箱：guo_yaqiong@126.com。

马进荣，博士，教授级高工。电子邮箱：jrma@nhri.cn。