基于长短时记忆网络的旋转机械状态预测研究

赵建鹏，周 俊

(上海工程技术大学 机械工程学院，上海 201620）

基于长短时记忆网络的旋转机械状态预测研究

赵建鹏，周 俊

(上海工程技术大学 机械工程学院，上海 201620）

作为深度学习算法的一种，长短时记忆网络越来越成为时间序列预测的重要手段，简要阐述长短时记忆网络的基本原理，并将其应用于旋转机械状态监控领域，以轴承数据为样本进行仿真，针对轴承数据的非平稳性，运用经验模态分解方法将其分解为平稳信号，并计算其本征模态分量能量熵作为状态特征，通过计算长短时记忆网络对旋转机械状态单步预测的结果，并与支持向量回归机模型的预测结果进行比较，证明长短时记忆网络在旋转机械状态预测方面可以取得比支持向量回归机更好的效果。

振动与波；长短时记忆；故障预测；状态监控；经验模态分解；能量熵

随着现代大型机械装备日益趋于复杂化、高速化、自动化与精密化，部件之间相互耦合的关系越来越强，一旦其中一个关键部件发生故障，往往会引发机械故障的一系列“链式反应”，从而造成工厂的财产损失甚至是人员伤亡。尤其对于旋转机械来说，其所受载荷为动态载荷，更易发生机械故障，故而对于旋转机械的状态监控和预测一直是研究的热点[1]。

对机械设备进行故障诊断和预测的方法可以分为三种，分别是基于数据驱动的方法、基于模型的方法和基于经验方法。其中基于数据驱动的方法主要应用神经网络、马尔可夫模型等机器学习方法，随着机器学习在今天生产和生活各个领域的广泛应用而获得巨大发展，成为最主要的故障诊断和预测方法。学界也提出了很多基于机器学习的机械故障预测方法[2–6]。

标准神经网络在应对分类任务时很有效，能够对非线性系统进行良好的拟合，但是由于在神经网络的假设中所取得的数据被视为互相独立的，无法模拟时间序列中的马尔可夫过程，所以提出了递归神经网络(Recurrent Neural Network,RNN)模型，下一时刻的输出状态y(t+1)不仅依赖于下一时刻的输入x(t+1)，而且依赖于本时刻的输出状态y(t)。Yam等提出以递归神经网络作为视情维修手段，构建了面向机械状态的智能预测决定支持系统[7]。Wang等提出以动态小波神经网络(Dynamic Wavelet Neural Network,DWNN)和虚拟传感器作为“测量(measure)”故障增长和预测剩余使用寿命的手段[8]。这些文献表明，递归神经网络在机械状态预测方面的确具有其优越性，能够产生良好的效果，但是RNN也具有一些缺陷，比如难以训练并且无法学习长期依赖关系等，作为其改进版本，长短时记忆(Long Short-Term Memory,LSTM)网络自提出至今尚未被应用于机械状态预测领域。

文中提出以LSTM网络作为机械状态监控和预测的方法，分为两步，第一步进行特征提取，对轴承振动数据进行经验模态分解，并以分解得到的IMF能量熵之和作为机械状态特征，第二步设计LSTM网络的结构并进行仿真验证，由于支持向量回归机(Support Vector Regression Machine，SVRM)模型近年来在时间序列预测方面取得很多令人振奋的结论，所以将LSTM网络的仿真结果与根据SVRM模型得到的结果进行比较。表明相比于SVRM模型，LSTM网络能够更好地逼近真实值。而且SVRM模型存在参数优化问题，惩罚因子和核函数参数的选取严重影响其预测性能,而LSTM网络则有效避免了参数选取的难题。本研究推广了长短时记忆网络的应用领域，提出了一种旋转机械状态监控和预测的新方法。

1 LSTM网络简介

1.1 RNN原理

RNN神经元的结构与标准神经元的区别在于其具有递归结构，可以将上一个状态的信息传递到当前状态，如图1所示，当输入为时间序列时，可以将其展开为一系列相互连接的标准神经元。

图1 递归神经网络神经元结构图

设输入序列为X=(x1,x2,…,xt)，隐单元序列H=(h1,h2,…,ht)与输出序列Y=(y1,y2,…,yt)的算法为

σ为非线性激活函数，Wxh、Whh、Why分别为输入到隐单元、隐单元到隐单元、隐单元到输出的权值矩阵，bh、by分别为隐单元和输出的偏置项。

1.2 LSTM网络原理

LSTM网络是一种应用于深度学习领域的RNN，由Hochreiter和Schmidhuber（1997）提出以克服RNN难以训练和梯度消失问题[9]，能够学习长期依赖关系，之后被学界不断完善[10–11].

LSTM网络与标准RNN的区别在于RNN的隐单元的结构被长短时记忆网络以记忆块代替，记忆块中最重要的结构是其所具有的三个门结构和一个元胞(cell)结构。其具体构造如图2所示。

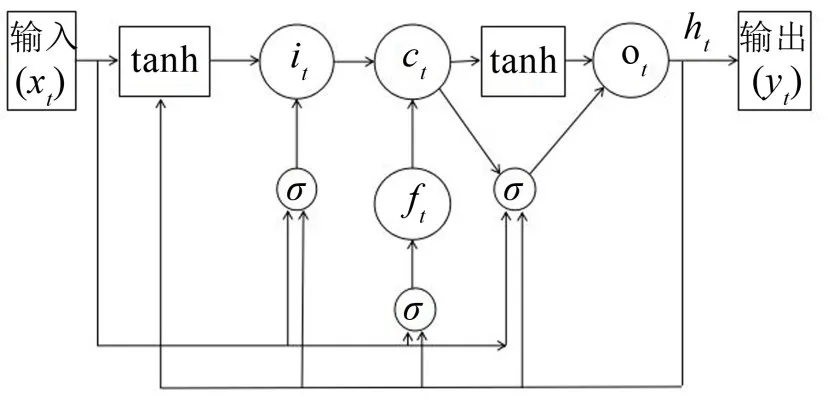
图2 长短时记忆网络记忆块结构

在LSTM网络中三个门结构采用的Logistic sigmoid函数所起的作用是通过控制门的开关程度控制信息的流动，在方程式(5)计算状态ct的过程中，输入门控制输入的比率，以当前层的输入xt和上一时刻隐单元的输出ht-1作为输入，输出结果it作为将要更新的信息

遗忘门控制所通过的先前记忆的比率，输出结果ft

遗忘门的输出结果与旧的元胞状态ct-1相乘，用以遗忘信息，输入门的输出it与tanh层相乘作为新的候选信息，二者之和生成新的元胞状态ct

输出门决定是否通过当前的记忆，输出结果ot，tanh层处理新的元胞状态，二者相乘作为隐单元的输出

最后获得输出信息

σ为 Logistic sigmoid 函数，it、ft、ot、ct分别为t时刻的输入门、遗忘门、输出门、元胞结构的状态，Wxi、Wxf、Wxo、Wxc分别为从输入到输入门、遗忘门、输出门和元胞结构的权值矩阵，Whi、Whf、Who、Whc分别为从隐单元到输入门、遗忘门、输出门和元胞结构的权值矩阵，Φ为网络输出激活函数，选用Re LU(Rectified Linear Units)函数作为激活函数。

LSTM网络的训练算法采用通过时间的反向传播算法(Back Propagation Through Time,BPTT)算法进行训练[12]。

1.3 基于LSTM的旋转机械状态预测建模

旋转机械在运行过程中的特征可以被视为时间序列，设旋转机械有n个特征值，且当前时刻t的状态与此时刻之前k个状态有关，即输入向量为

其中下标表示特征种类，上标表示每种特征中与当前状态相关的特征，如表示在第n种特征中当前时间t之前的第k个特征值。

图3 LSTM网络结构

其中输入层节点数即需要输入的特征的个数，其数量为input_num=n×k输出层节点数，即当前状态的特征种类，其数量为output_num=n隐层节点数，由经验确定。

2 实验验证

2.1 数据介绍

由于旋转机械最重要的结构是轴承转子系统，为了验证LSTM网络在旋转机械状态预测方面的效果，在尽可能降低实验成本并且能取得相同实验效果的条件下，可以只采用轴承转子系统全寿命数据，文中的数据采用美国辛辛那提大学(University of Cincinnati)智能维护系统(Intelligent Maintenance Systems,IMS)中心轴承全寿命数据集，其实验所用的传感器为PCB 353B33 High Sensitivity Quartz ICP加速度传感器，所用轴承为Rexnord ZA-2115 double row bearings，轴承试验台与传感器的安装情况分别如图4、图5所示。

图4 轴承试验台

图5 传感器布置图

采样频率为20 kHz，每次采样20 480点。选取其中第二个数据集(Set No.2)，每10 min采样一次，在实验的最后阶段，轴承1的外圈发生故障，实验终止[14]。

2.2 特征提取

由于振动试验所获得的信号为非平稳、非线性信号，因此需要对每次采样的数据进行平稳化处理，实验表明，经验模态分解(Empirical Mode Decomposition,EMD)方法作为一种重要的数据平稳化方法，具有良好的效果[15]。

设给定的时间序列为x(t)，经过经验模态分解得到n个平稳固有模态分量(Intrinsic Mode Function，IMF)ci(t)和一个残余分量r(t)，即

以数据集的第一个数据为例，其EMD分解结果如图6所示。

刨除最后的残余分量r(t)，以分解后的13个IMF的能量熵(energy entropy)之和作为特征值[16]，提取能量熵作为轴承故障特征,能量熵值的大小反映信号概率分布的均匀程度,结合能量与熵，可以表征机械状态的平稳程度，其定义为

图6 EMD分解效果图

E表征信号的总能量，Ei表征第i个IMF分量的能量，Pi表征第i个IMF分量占总能量的百分比。经过仿真计算，最终可以得到EMD能量熵的变化趋势。

2.3 LSTM与SVR预测结果比较

接下来设计LSTM网络的结构，由于其输出值y(t+1)是一维特征值，故其输出节点都设计为1，其输入值的维数即是时间窗口宽度(Time window width)，故输入节点设计为时间窗口宽度。

以所选数据集中的前67%的数据为训练集(Train set)，以余下的数据作为测试集(Test set)，为了比较LSTM与SVRM两个算法的优劣，分别计算时间窗口宽度为3和10两种情况下的机械状态单步预测结果,时间窗口宽度为3时隐层节点数设计为5，时间窗口宽度为10时隐层节点数设计为13，为了与SVRM算法相比较，隐层只取一层。SVRM算法选用Matlab的Libsvm工具包中的函数[17]，最后以均方误差(Mean squared error,MSE)为指标来比较LSTM与SVRM对机械状态的预测能力。

其中yi为所预测的机械状态输出值，ŷi为机械状态的实际值。

时间窗口宽度为3时，LSTM算法仿真所得的预测效果如图7所示。

时间窗口宽度为3时，SVRM算法仿真所得的预测效果如图8所示(当惩罚因子c=1 670、核函数参数g=0.06时，MSE取得最小值)。

图7 LSTM预测效果图(窗口宽度为3)

图8 SVRM预测效果图(窗口宽度为3)

时间窗口宽度设定为10时，LSTM算法仿真所得的预测效果如图9所示。

图9 LSTM预测效果图(窗口宽度为10)

时间窗口宽度为10时，SVRM算法仿真所得的预测效果如图10所示(当惩罚因子c=265、核函数参数g=0.06时，MSE取得最小值)：

图10 SVRM预测效果图(窗口宽度为10)

两种算法的比较结果如表1所示。

表1 LSTM与SVRM预测误差比较

通过两种方法的预测误差比较可以发现，同一窗口宽度下LSTM比SVRM能够更好地逼近真实值。

3 结语

提出一种机械状态监控与预测的新算法—LSTM网络算法，以经过EMD分解获得的IMF的能量熵之和作为状态特征，通过设计不同的时间窗口宽度对LSTM网络和SVRM两种方法的机械状态单步预测效果(训练MSE和测试MSE)进行比较可以发现，当窗口宽度相同时，LSTM网络测试结果的MSE都比SVRM测试结果的MSE要小，表明提出的LSTM模型所固有的结构优势使得其在机械状态监控与预测方面能够取得比SVRM模型更好的结果，而且有效避免了SVRM模型的参数选择难题，随着当今深度学习方法的不断发展和改进，LSTM网络将会在轴承、齿轮、切削刀具等机械关键部件的状态监控与预测方面具有更加广阔的应用前景。

[1]ISERMANN R.Supervision,fault-detection and faultdiagnosis methods- An introduction[J].Control Engineering Practice,1997,5(5):639-652.

[2]王涛，李艾华，高运广，等.基于相空间重构和遗传优化SVR的机械设备状态趋势预测[J].噪声与振动控制，2014，34(3)：176-181.

[3]ZHANG C,LIM P,QIN A K,et al.Multiobjective deep beliefnetworksensemble forremaining usefullife estimation in prognostics[J].IEEE Transactionson Neural Networks&Learning Systems,2016:1-13.

[4]TOBON MEJIA D A,MEDJAHER K,ZERHOUNI N,et al.A data-driven failure prognostics method based on mixture of gaussians hidden markov models[J].IEEE Transactions on Reliability,2012,61(2):491-503.

[5]宋梅村，蔡琦.基于支持向量回归的设备故障趋势预测[J].原子能科学技术，2011，45(8)：972-976.

[6]JIA F,LEI Y,LIN J,et al.Deep neural networks:A promising toolfor faultcharacteristic mining and intelligent diagnosis of rotating machinery with massive data[J].Mechanical Systems&Signal Processing,2015,72-73:303-315.

[7]YAM R C M,TSE P W,LI L,et al.Intelligent predictive decision support system for condition-based maintenance[J].TheInternationalJournalofAdvanced Manufacturing Technology,2001,17(5):383-391.

[8]WANG,PENG.Fault prognostics using dynamic wavelet neural networks[J].ArtificialIntelligencefor Engineering Design Analysis&Manufacturing,2001,15(15):349-365.

[9]HOCHREITER S,SCHMIDHUBER J.Long short-term memory[J].Neural Computation,1997,9(8):1735-1780.

[10]SUTSKEVER I,VINYALS O,LE Q V,et al.Sequence to sequence learning with neural networks[C].Advances in Neural Information Processing Systems,2014,4:3104-3112.

[11]GERS F A,SCHMIDHUBER J,CUMMINS F.Learning to forget:continual prediction with LSTM[J].Neural Computation,2000,12(10):2451-71.

[12]GRAVES A.Supervised sequence labelling with recurrent neural networks[M].Springer Berlin Heidelberg,2012.

[13]MARCHI E,VESPERINI F,WENINGER F,et al.Nonlinear prediction with LSTM recurrent neural networks for acoustic novelty detection[C].IJCNN,2015:13395-13408.

[14]QIU H,LEE J,LIN J,et al.Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J].Journal of Sound&Vibration,2006,289(4-5):1066-1090.

[15]PING J S,WOO W L,SULAIMAN H A,et al.Advances in machine learning and signal processing[M].Springer International Publishing,2016.

[16]YU Y,YU DEJIE,CHENG J.A roller bearing fault diagnosis method based on EMD energy entropy and ANN[J].Journal of Sound&Vibration,2006,294(1-2):269-277.

[17]FAN R E,CHEN P H,LIN C J.Working set selection using second order information for training support vectormachines[J].JournalofMachineLearning Research,2005,6(4):1889-1918.

State Prognosis of Rotary Machines Based on Long/Short Term Memory Recurrent Neural Network

ZHAO Jian-peng,ZHOU Jun
(School of Mechanical Engineering,Shanghai University of Engineering Science,Shanghai 201620,China)

As a method of deep learning algorithm,long/short term memory network(LSTM)has been playing an increasingly important role in the field of time series prediction.In this paper,a new method for state prediction of rotary machines based LSTM is proposed.And the principle of LSTM applied to rotary machine state monitoring and prognosis is introduced and applied to state monitoring of the rotary machinery.In order to avoid the instability of the bearing data,the empirical mode decomposition(EMD)is used to decompose the bearing data into several steady signals,and the intrinsic mode function(IMF)energy entropy is calculated as the feature of the machine state.Furthermore the analysis of simulation results based on LSTM is compared with those of support vector regression machine(SVRM).LSTM has achieved a stateof-the-art prediction performance in the single-step prediction of rotary machine states.It is shown that the proposed prognosis technology is superior in rotary machine state prediction and monitoring.

vibration and wave;LSTM;fault prognosis;state monitoring;EMD;energy entropy

TP206.3

：A

：10.3969/j.issn.1006-1355.2017.04.030

1006-1355(2017)04-0155-05

2017-01-16

教育部留学回国人员科研启动基金资助项目(教外司留[2012]940号)

赵建鹏（1991－）男，山东省泰安市人，硕士生，主要研究方向为故障诊断与预测。

周俊，女，硕士生导师。

E-mail:shuu_shun@163.com